海洋垂线偏差对海基站空间目标定位精度的影响*

向 颉，茅永兴，李晓勇，李辉芬，陈红英(中国卫星海上测控部,江苏江阴214431)



海洋垂线偏差对海基站空间目标定位精度的影响*

向 颉**，茅永兴，李晓勇，李辉芬，陈红英
(中国卫星海上测控部,江苏江阴214431)

**通信作者:xiangjie100@163. com Corresponding author:xiangjie100@163. com

摘 要:在处理海基站跟踪空间目标的测量数据时,需要将瞬时站址惯导地平坐标系(垂线坐标系)转换至当地法线坐标系,这一过程需要使用当地重力垂线偏差数据。因航天远洋测量船深处远离大陆的大洋,缺少所需的垂线偏差数据,因而常将垂线坐标系当成法线坐标系使用,从而对海基站目标空间定位精度产生了影响。在发射坐标系和J2000地心惯性坐标系下,分析了考虑和不考虑垂线偏差因素的模型差异,并且对发射段、运行段等不同飞行高度的空间目标进行了定位精度仿真计算,给出了垂线偏差对空间目标定位精度影响的初步结论。结果表明,当垂线偏差横向、纵向分为10″时,空间目标定位精度的影响最大能达200 m。因此,数据处理时必须对测量数据进行海洋垂线偏差修正。

关键词:海基测量；空间定位；垂线偏差；定位精度

1 引 言

由于地球本身是一形状不规则、质量分布不均匀的球体,从而使得当地的铅垂线方向与参考椭球体的法线方向不一致,它们之间的差异就是垂线偏差u,并定义其在子午面上的分量为ξ、在卯酉面上的分量为η[1]。国内外学者的研究成果表明,不同海域的海洋垂线偏差为数角秒至数十角秒不等[2],在海山、海沟及岛礁附近,垂线偏差通常较大,达到数十角秒,远大于测量船的姿态测量误差;而在海底平坦区域,垂线偏差通常较小,但也与测量船的变形测量误差相当。

对于陆上固定测控站、发射场发射工位等,通过天文大地测量法[3]、重力测量法[4]、天文重力测量法和GPS测量法等多种手段[5],将其垂线偏差进行精确标定,并且在较长一段时间内其值是固定不变的,因此,陆上固定站提供用户使用的空间目标测量数据是已进行垂线偏差修正的测站法线坐标系下的。

对于海基站,由于雷达设备的安装平台是海基移动平台,其位置、姿态是实时变化的。为此,海基站提供用户使用的测量数据的基准坐标系为瞬时站址惯导地平坐标系,其坐标系原点通过卫导或惯导系统实测精确定位得到,其基准面为当地水平面,由惯导系统实时测量得到。海基站的瞬时站址惯导地平坐标系实际上是一垂线坐标系,它与当地参考椭球体的法线方向存在一定的差异——垂线偏差,而用户需要海基站提供的是法线坐标系下的数据,这样才能完成一系列坐标系转换,从而实现在J2000地心惯性坐标系下的弹道与轨道计算。然而,传统垂线偏差测量方法不适用于海基站动平台测量,因此,以前没有技术手段建立海洋垂线偏差数值模型以实时获取海基站任务海域的垂线偏差数据,只能将瞬时站址惯导地平坐标系(垂线坐标系)默认为当地法线测量坐标系,使得垂线偏差作为一种误差项直接引到入弹道、轨道计算结果中,从而影响了弹道、轨道的计算精度。

近30年来,在多代卫星测高计划的支持下,海洋重力场的确定得到了迅速发展。同时,所积累的大量卫星测高数据集,为地球物理学、大地测量学、海洋学的应用提供了丰富的信息源。而海洋区域的垂线偏差作为许多应用的基础数据,正受到越来越高的重视。海洋垂线偏差的测量一直是许多学者研究的课题。目前,国内已经提出了基于卫星测高数据的海洋垂线偏差计算、基于重力异常测量数据的海洋垂线偏差计算等方法,这些方法不仅可以使用于近海而且可以使用于远海的垂线偏差测量计算。国内学者也根据这些方法建立了我国东南沿海海域垂线偏差2'×2'网格化数值模型[6-7],该模型分辨率最高可达10-4角秒,为我国近海海域航天精密测量提供了数据基础。但航天测量船的测量海域大多数在远离大陆的广阔大洋上,对应海域目前尚无相应分辨率和精度更高的数值模型。因此,为提高海基站外测数据弹道、轨道计算的精度,迫切需要开展远海海域高精度、高分辨率海洋垂线偏差数值模型的建立以及实时计算方法方面的研究。

那么,海洋垂线偏差对海基站空间目标定位精度的影响究竟有多大?处理海基测量数据时是否需要修正垂线偏差?本文通过3个算例给出初步的结论。

2 海基站空间目标定位模型

海基站跟踪空间目标获取的原始测量数据为设备测量坐标系下,经海基平台摇摆、变形、视差等修正后,成为瞬时站址惯导地平坐标系下的测量数据,方可供用户进行弹道、轨道计算使用。

2.1 垂线发射坐标系下海基测量空间目标定位模型

航天器发射段,海基站对运载火箭的跟踪测量数据,经事后数据处理后,以垂线发射坐标系下的位置矢量的形式提供型号研制单位。由海基站瞬时站址惯导地平坐标系(垂线测量坐标系)下的空间目标测量数据ρ(斜距)、A(方位角)、h(俯仰角)计算垂线发射坐标系下空间目标位置矢量rf的计算模型为

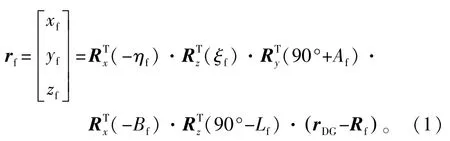
式中:ξf、ηf分别为发射点的垂线偏差在当地子午面和卯酉面上的分量;Lf、Bf、Af分别为发射点的大地经度、大地纬度和大地发射方位角;R(·)为旋转矩阵;rDG为空间目标在地心地固坐标系下的位置矢量;Rf为发射点在地心地固坐标系下的位置矢量。它们的计算模型为[8]

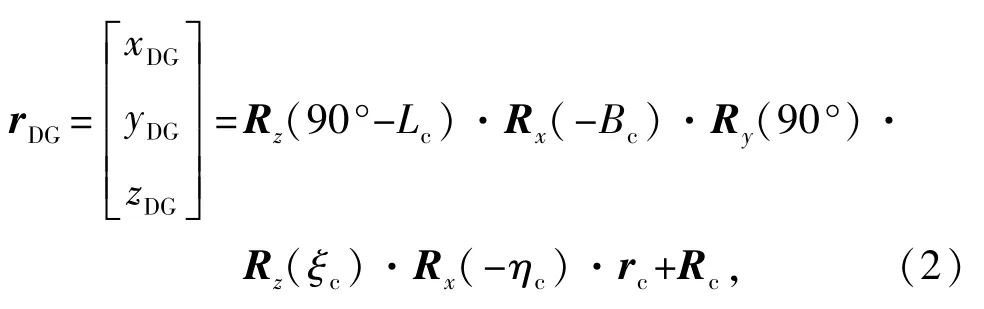
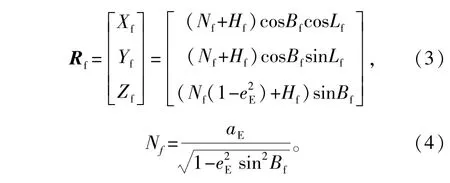
式中:ξc、ηc分别为海基站当地的垂线偏差在子午面和卯酉面上的分量;Lc、Bc分别为海基站的大地经度、大地纬度;Hf为发射点高程;αE为地球赤道平均半径;eE为地球参考椭球体第一偏心率;rc为空间目标在海基站瞬时站址惯导地平坐标系(垂线测量坐标系)下的位置矢量;Rc为海基站在地心地固坐标系下的位置矢量。它们的计算模型为

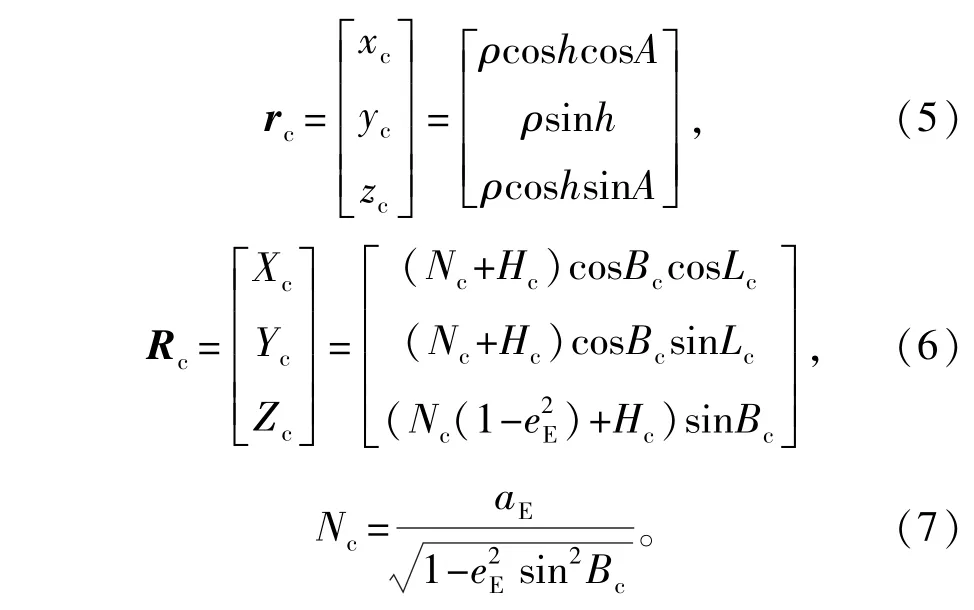
式中:Hc为海基站的高程。

若无法获取海基站任务海域的海洋垂线偏差ξc、ηc,则式(2)简化为

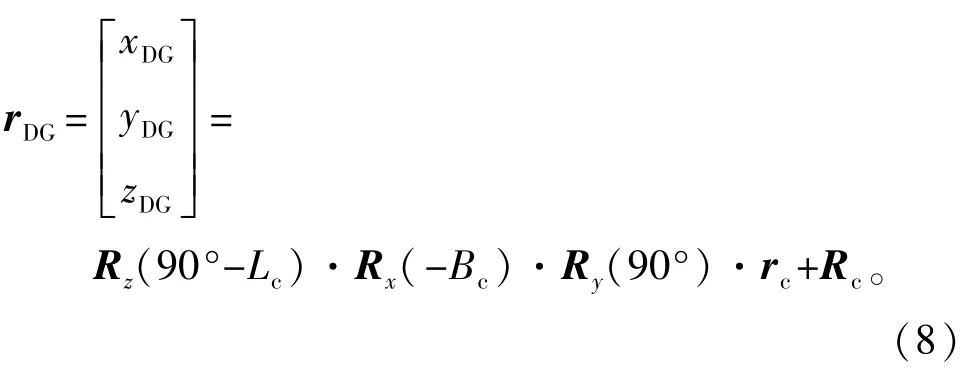
由此产生的误差直接被引入到垂线发射坐标系下空间目标位置矢量rf中。

2. 2 J2000地心惯性坐标系下海基测量空间目标

定位模型

对航天器运行段的跟踪测轨数据,主要用于对航天器的轨道确定,测轨数据精度的高低,直接影响轨道确定的精度。为检验跟踪测轨数据的精度,通常可以采用跟踪安装有卫导等高精度测轨系统的“标校星”或其他航天器,并与其精密星历数据进行比对的方法,方法1是将精密星历数据转换至测站坐标系(如瞬时站址惯导地平坐标系)下,以理论测元的形式与测量数据进行比对;方法2是将测量数据转换至J2000地心惯性坐标系下,以空间位置矢量的形式与精密星历数据进行比对。它们从测元精度和定位精度两个不同的角度检验测量数据的精度。这里给出方法2的计算模型。

由式(2)或式(8)已计算得到空间目标在地心地固坐标系下的位置矢量rDG,则计算J2000地心惯性坐标系下的位置矢量rJ2000的计算模型为[9]

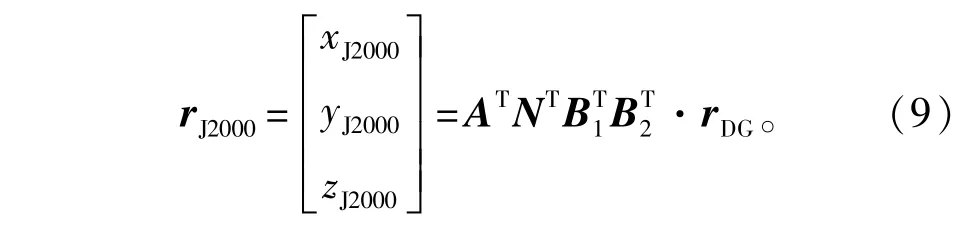
式中:ζA、zA、θA为赤道面进动的3个欧拉角(赤道岁差角);εA、Δψ、Δε分别为平黄交角、黄经章动、交角章动;SG为格林尼治真恒星时;xp、yp为极移的两个分量。

同样,若无法获取海基站测量海域的海洋垂线偏差ξc、ηc,由此产生的误差直接被引入到J2000地心惯性坐标系下空间目标位置矢量rJ2000中。

3 算例分析

3. 1 算例1:运载火箭发射段海基测量空间定位计算结果

我们使用某航天器发射任务中海基站对运载火箭(飞行轨道高度约200 km)的跟踪测轨数据,计算运载火箭在垂线发射坐标系下的空间定位结果。表1给出了跟踪仰角分别为10°、20°、30°、40°、50°时,修正与不修正任务海域垂线偏差的空间定位结果及其差异;表2给出了跟踪仰角10°～20°、20°～30°、30°～40°、40°～50°区间内修正与不修正任务海域垂线偏差的空间定位偏差的统计结果,其中,A表示不修正垂线偏差,B表示修正垂线偏差,B-A表示两者的差异;任务测量海域垂线偏差取值为ξ=10″,η=10″,下同。

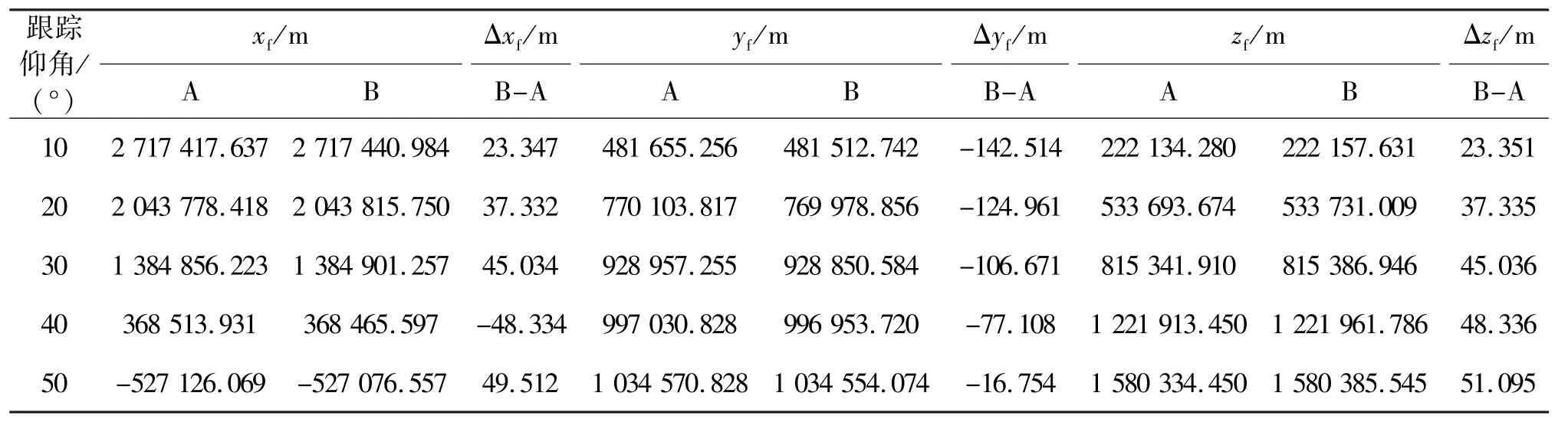
表1 运载火箭在垂线发射坐标系下的空间定位结果Tab. 1 Rocket localization in vertical launching coordinate system

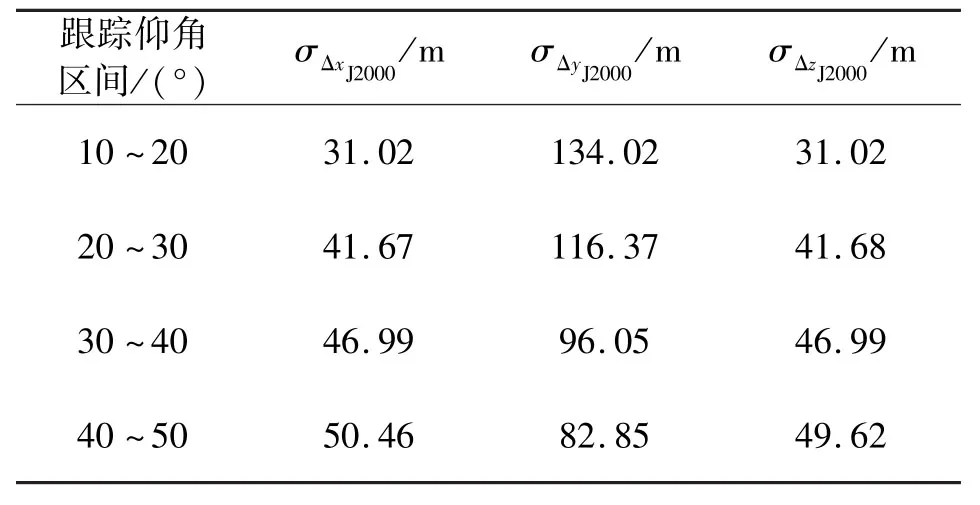
表2 运载火箭在垂线发射坐标系下的空间定位偏差统计结果Tab. 2 Statistical results of rocket localization in vertical launching coordinate system

3. 2 算例2:低轨航天器运行段海基测量空间定位计算结果

我们使用某次载人飞船发射任务中海基站对飞船运行段(飞行轨道高度约340 km)的跟踪测轨数据,计算飞船在J2000地心惯性坐标系下的空间定位结果。表3给出了跟踪仰角分别为10°、20°、30°、40°、50°时,修正与不修正任务海域垂线偏差的空间定位结果及其差异;表4给出了跟踪仰角10°～20°、20°～30°、30°～40°、40°～50°区间内,修正与不修正任务海域垂线偏差的空间定位偏差的统计结果。

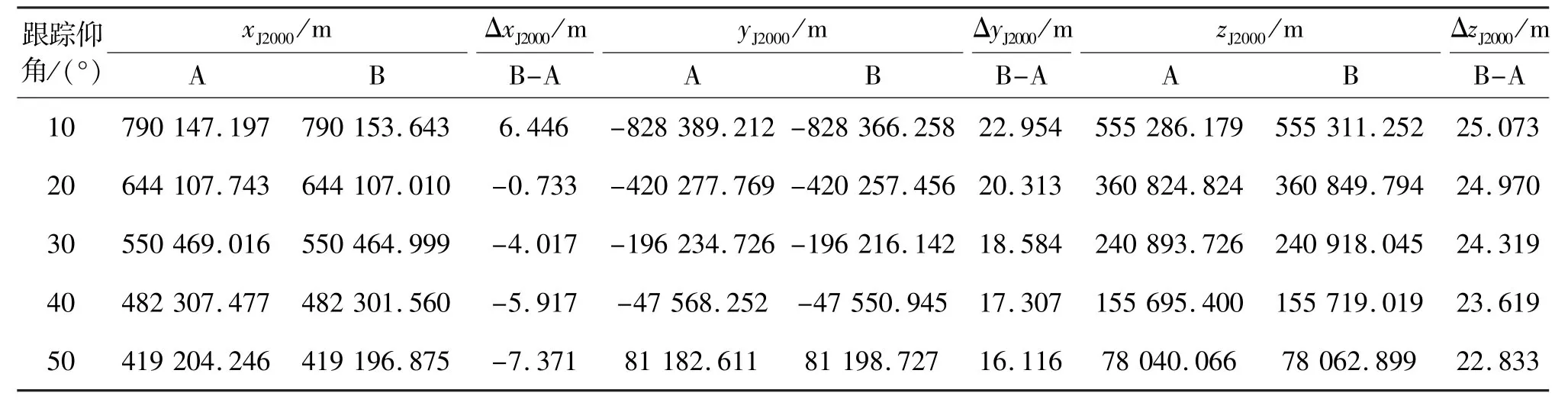
表3 飞船在J2000地心惯性坐标系下的空间定位结果Tab. 3 Spaceship localization in J2000 inertial coordinate system

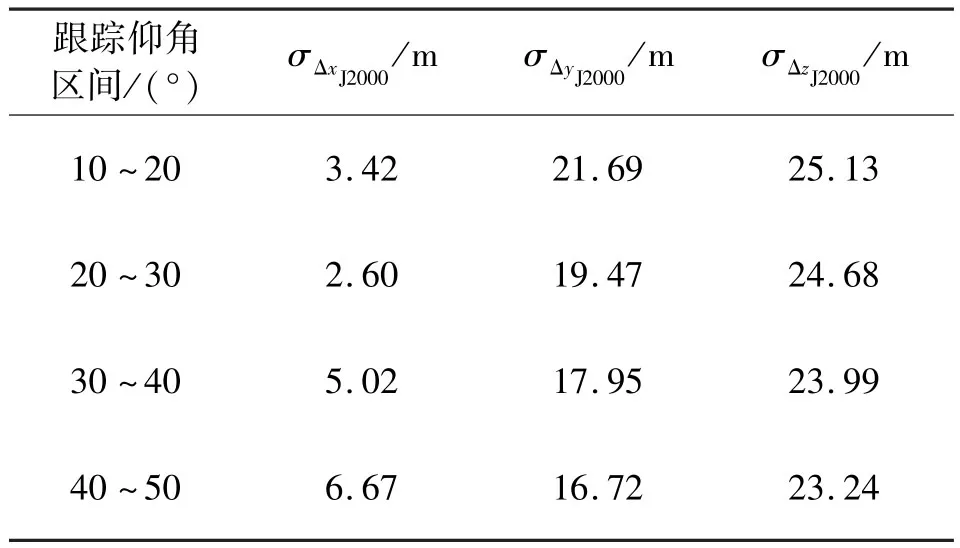
表4 飞船在J2000地心惯性坐标系下的空间定位偏差统计结果Tab. 4 Statistical results of spaceship localization in J2000 inertial coordinate system

3. 3 算例3:高轨航天器运行段海基测量空间定位计算结果

个人所得税可以统筹财政收入，而且可以调整社会经济，由于属于直接税，通过和财政收入的比较能够看出，调节居民收入分配以及保障社会公平是比较重要的。这次个税修正草案把各种劳动所得综合成综合所得，确保个税征收模式在综合和分类相联系的时候能够更加顺利。

我们使用某次同步卫星发射任务中海基站对卫星同步转移轨道段(测轨数据段的卫星飞行轨道高度约20 000 km)的跟踪测轨数据,计算卫星在J2000地心惯性坐标系下的空间定位结果。表5给出了跟踪仰角分别为10°、20°、30°、40°、50°时,修正与不修正任务海域垂线偏差的空间定位结果及其差异;表6给出了跟踪仰角10°～20°、20°～30°、30°～40°、40°～50°区间内,修正与不修正任务海域垂线偏差的空间定位偏差的统计结果。

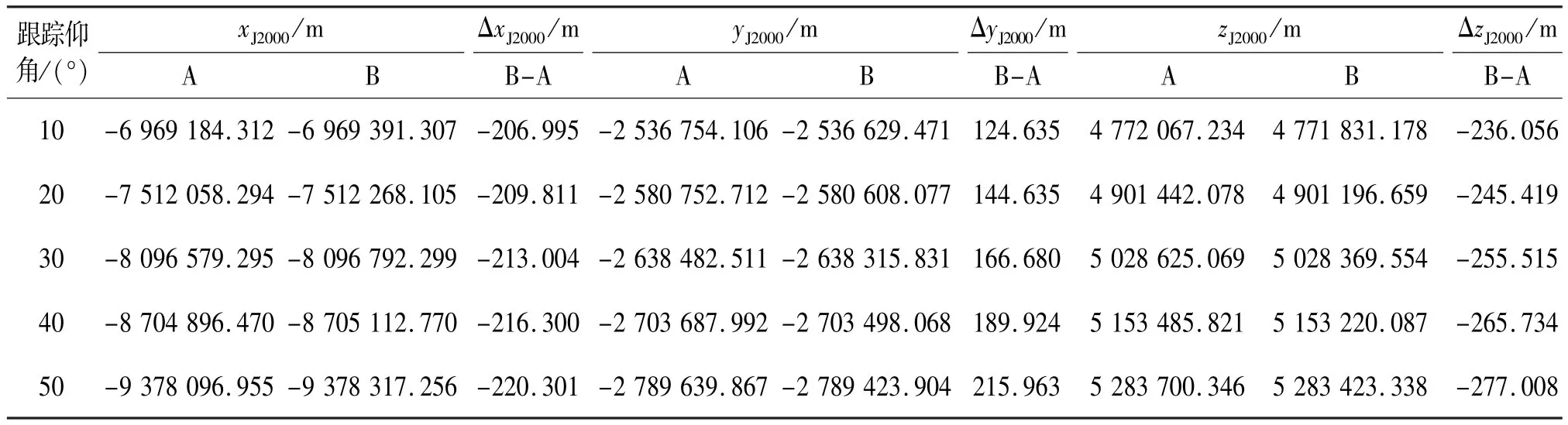
表5 卫星在J2000地心惯性坐标系下的空间定位结果Tab. 5 Satellite localization in J2000 inertial coordinate system

表6 卫星在J2000地心惯性坐标系下的空间定位偏差统计结果Tab. 6 Statistical results of satellite localization in J2000 inertial coordinate system

3. 4 结果分析

从计算结果来看,当任务测量海域的垂线偏差达到ξ=10″、η=10″时,对于发射段飞行轨道较低的运载火箭,海洋垂线偏差对垂线发射坐标系下的空间定位结果的影响达到-142. 5～51. 1 m;对于飞船运行段,海洋垂线偏差对J2000地心惯性坐标系下的空间定位结果的影响达到-7. 0～25. 1 m;对于同步转移轨道段远地点附近的卫星,海洋垂线偏差对J2000地心惯性坐标系下的空间定位结果的影响达到-277. 0～215. 9 m。而海基测量的任务海域是不固定的,因而海洋垂线偏差的大小也是不固定的,如果任务测量海域处于群岛、岛礁、海山、海沟附近,则海洋垂线偏差值更大(最大可达到30″以上),从而对运载火箭和航天器的空间定位结果的影响也更大。因此,为了提高海上测量精度或者说提高对海上测量数据使用时的处理精度,必须进行海洋垂线偏差修正。修正垂线偏差在具体实施时,可根据需要选择垂线发射坐标系下海基测量空间目标定位模型或J2000地心惯性坐标系下海基测量空间目标定位模型。

4 结束语

本文用3个算例分析了海洋垂线偏差对运载火箭和航天器空间定位精度的影响,旨在给广大读者一个启示。要重视广阔海洋的高分辨率垂线偏差数值模型的研究,需要建立我国专用的高精度高分辨率海洋垂线偏差数值模型,为我国航天器的高精度测量以及国防现代化建设奠定基础。由于目前国内尚未建立完善的远洋垂线偏差精确数学模型,本文的数据都为仿真数据,分析时结合了近海垂线偏差网格数值模型,只给出了空间定位结果的影响范围,未使用实际偏差数据进行验证。因此,还需要在取得具体远洋海域垂线偏差的基础上,对远洋航天测量垂线偏差的影响进一步研究。

参考文献:

[1] 孔祥元.大地测量学基础[M].武汉:武汉大学出版社,2010.

KONG Xiangyuan. Foundation of geodesy[M]. Wuhan: Wuhan University Press,2010. (in Chinese)

[2] 肖荣健,邹强.垂线偏差的确定方法[J].大众科技, 2009,120(8):58-59.

XIAO Rongjian,ZOU Qiang. Determination of deflection of the vertical[J]. Popular Science & Technology,2009, 120(8):58-59. (in Chinese)

[3] 郭金运,宋来勇,常晓涛,等.数字天顶摄像仪确定垂线偏差及其精度分析[J].武汉大学学报(信息科学版),2011,39(9):1086-1088.

GUO Jinyun,SONG Laiyong,CHANG Xiaotao,et al. Vertical deflection measure with digital zenith camera and accuracy analysis[J]. Geomatics and Information Science of Wuhan University,2011,39(9):1086-1088. (in Chinese)

[4] 胡淑梅,文汉江,李洪超,等.利用多种测高数据反演中国南海海域重力异常[J].大地测量与地球动力学, 2011,31(4):56-59.

HU Shumei,WEN Hanjiang,LI Hongchao,et al. Inversion of gravity anomalies over south China sea by use of combination of multi-satellite altimeter data[J]. Journal of Geodesy and Geodynamics, 2011, 31 ( 4 ): 56 - 59. (in Chinese)

[5] 柴华,王勇,王虎彪,等. GNSS/ SINS组合进行惯性重力测量误差分析[J].大地测量与地球动力学,2011, 31(6):73-78.

CHAI Hua,WANG Yong,WANG Hubiao,et al. Error analysis for inertial gravimetry by use of GNSS / Sins combination[J]. Journal of Geodesy and Geodynamics,2011, 31(6):73-78. (in Chinese)

[6] 王虎彪,王勇,陆洋.联合多种测高数据确定中国边缘海及全球海域的垂线偏差[J].武汉大学学报(信息科学版),2007,32(9):770-773.

WANG Hubiao,WANG Yong,LU Yang. Improve deflection of the vertical in China marginal sea together with multi-altimeter data[J]. Geomatics and Information Science of Wuhan University,2007,32(9):770-773. (in Chinese)

[7] 邓凯亮,暴景阳,章传银,等.联合多代卫星测高数据建立中国近海垂线偏差模型[J].海洋测绘,2008,28 (3):15-17.

DENG Kailiang,FU Jingyang,ZHANG Chuanyin,et al. Determination of vertical deflection over China sea by combination of multi-satellite altimeter data[J]. Hydrographic Surveying and Charting,2008,28(3):15-17. (in Chinese)

[8] 茅永兴.航天器轨道确定的单位矢量法[M].北京:国防工业出版社,2009.

MAO Yongxing. Unit vector method of spacecraft orbit determination [ M]. Beijing: National Defense Industry Press,2009. (in Chinese)

[9] 李济生.人造航天器精密轨道确定[M].北京:解放军出版社,1995.

LI Jisheng. Precise orbit determination of spacecraft [M]. Beijing:PLA Press,1995. (in Chinese)

向 颉(1982—),男,湖南龙山人,2014年于南京理工大学获硕士学位,现为工程师,主要研究方向为航天数据处理与精度分析;

XIANG Jie was born in Longshan,Hunan Province,in 1982. He received the M. S. degree from Nanjing University of Science and Technology in 2014. He is now an engineer. His research concerns aerocraft maritime measurement data processing and accuracy analysis.

Email:xiangjie100@163. com

茅永兴(1966—),男,江苏南通人,2005年获硕士学位,现为研究员,主要从事航天测控技术以及轨道确定方法研究;

MAO Yongxing was born in Nantong,Jiangsu Province,in 1966. He received the M. S. degree in 2005. He is now a senior engineer of professor. His research concerns aerospace TT&C and orbit determination.

Email:myx8282@ tom. com

李晓勇(1962—),男,湖南新宁人,高级工程师,主要研究方向为弹道数据处理与精度分析;

LI Xiaoyong was born in Xinning, Hunan Province, in 1962. He is now a senior engineer . His research concerns aerocraft trajectory data processing and accuracy analysis.

李辉芬(1968—),女,云南昭通人,硕士,研究员,主要研究方向为海上测量数据处理与精度分析;

LI Huifen was born in Zhaotong,Yunnan Province,in 1968. She is now a senior engineer of professor with the M. S. degree. Her research concerns maritime measurement data processing and accuracy analysis.

陈红英(1982—),女,四川营山人,2005年获硕士学位,现为工程师,主要研究方向为海上测量数据处理与精度分析。

CHEN Hongying was born in Yingshan,Sichuan Province, in 1982. She received the M. S. degree in 2005. She is now an engineer. Her research concerns maritime measurement data processing and accuracy analysis.

Influence of Deflection Vertical on Object Localization Accuracy in Aerocraft Measurement on Sea Base

XIANG Jie,MAO Yongxing,LI Xiaoyong,LI Huifen,CHEN Hongying
(China Satellite Maritime Tracking and Control Department,Jiangyin 214431,China)

Abstract:The inertial navigation horizontal coordinate system(vertical coordinate system) needs to be transformed into the local normal coordinate system in data processing of aerocraft measurement on sea base. In this progress,the local deflection vertical data is required. On the ocean away from the mainland, the deflection vertical data is lack. The vertical coordinate system is often used as the local normal coordinate system. The accuracy of object localization in aerocraft measurement on sea base is affected. In launch coordinate system and J2000 inertial system,the difference between object location model with deflection vertical and without deflection vertical is studied. The influence simulation calculation is performed for object localization model by 3 samples. The result is provided during rocket ascent and aerocraft in stage. When deflection vertical equals to 10 seconds of arc,the influence on object localization result can reach up to 200 meters. For improving aerocraft measurement accuracy on sea base,deflection vertical of aerocraft measurement data must be corrected.

Key words:aerocraft measurement on sea base;space localization;deflection vertical;localization accuracy

doi:10. 3969/ j. issn. 1001-893x. 2016. 02. 020引用格式:霍跃华,刘银龙.内容中心网络中安全问题研究综述[J].电讯技术,2016,56(2):224-232. [HUO Yuehua,LIU Yinlong. Survey on security issues in content-centric networking[J]. Telecommunication Engineering,2016,56(2):224-232. ]

作者简介:

中图分类号:TN911；V557

文献标志码:A

文章编号:1001-893X(2016)02-0218-06

*收稿日期:2015-05-15;修回日期:2015-08-11 Received date:2015-05-15;Revised date:2015-08-11