隐函数形式曲线的曲率和挠率的计算

黄　瑞，储亚伟（阜阳师范学院数学与统计学院，安徽阜阳236037）



隐函数形式曲线的曲率和挠率的计算

黄瑞，储亚伟
（阜阳师范学院数学与统计学院，安徽阜阳236037）

摘要：利用隐函数定理将平面曲线和空间曲线的一般方程化为微分几何中研究曲线的一元向量函数的形式，并使用微分几何中研究曲线的方法，将此类曲线的曲率和挠率的计算转化为实函数的偏微商的计算，从而实现对一般方程形式的曲线研究.

关键词：隐函数定理；曲率；挠率

0　引言

平面曲线和空间曲线是曲线论的两大研究对象，通过对曲线在一点处的渐近展开，曲线在该点处的曲率和挠率完全决定了曲线在该点邻近的近似形状，因此曲率和挠率是曲线的两个重要数字特征.在微分几何中，研究曲线时总是假设曲线的方程为一元向量函数的形式，文［1］给出形如r=(x(t),y(t))的平面曲线的曲率的计算公式，文［2］给出形如r=(x(t),y(t),z(t))的空间曲线的曲率和挠率的计算公式，文献［3，4］研究了具有某种特征的空间曲线的曲率和挠率.然而曲线的方程未必都能化为一元向量函数的形式，因此对一般方程形式的曲线的研究具有一定意义.本文将给出一般形式的曲线的曲率和挠率的计算公式及其在具体问题中的应用.

1　平面曲线(c):F(x,y)=0的曲率

设二元实函数F(x,y)在P(x,y)点的小邻域内满足隐函数定理［5］，不妨设Fy(x,y)≠0，则F(x,y)=0在x的小邻域内确定了唯一连续可导的隐函数y=f(x)，从而得到平面曲线(c):F(x,y)=0在x的小邻域内的一元向量函数形式.

证明不妨设平面曲线(c):F(x,y)=0在x的小邻域内可化为一元向量函数的形式r=(x,f(x))，其中y=f(x)为F(x,y)=0在x的小邻域内确定的隐函数.则

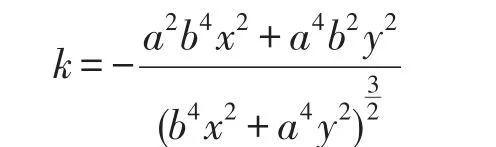
特别地，当a=b=r时，带入上式得到半径为r的圆的曲率为需要说明的是，平面曲线的曲率的符号反映了曲线的单位正法向量在单位圆周上的转动方向，单位正法向量逆时针转动时，曲率为正，单位正法向量顺时针转动时，曲率为负.

设曲面F(x,y,z)=0和G(x,y,z)=0相交，则交线为，也即是空间曲线的一般方程.设(c)在P(x,y,z)的小邻域内满足隐函数组定理的条件［5］，不妨设在P点的小邻域内确定了唯一连续可微的隐函数组x=φ(z),y=ψ(z)，从而空间曲线（c）在P点的小邻域内化为一元向量函数的形式r=(φ(z),ψ(z),z).

从而得到

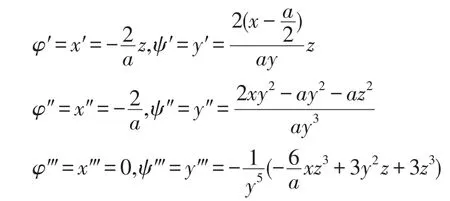
从而

代入定理2得

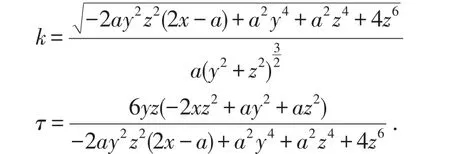
方法（二）.文［6］给出维维安尼曲线的一元向量函数的形式r=(acos2t,acostsint,asint)，并得到

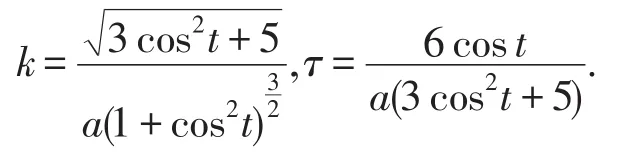
3　结束语

根据隐函数存在唯一性定理和可微性定理，文中将隐函数形式的曲线转化为微分几何中研究曲线的一元向量函数的形式，从而将曲线的曲率和挠率的计算转化为数学分析中的偏微商的计算，实现了对一般形式的曲线的研究.事实上，借助于这种转化，还能够求出隐函数形式的空间曲线在一点处的Frenet标架、切线、主法线、副法线、密切平面、从切平面和法平面等几何量.

参考文献：

［1］陈维桓.微分几何［M］.北京：北京大学出版社，2006：73.

［2］梅向明，黄敬之.微分几何［M］.北京：高等教育出版社，2008：42－43.

［3］刘学泳，滕超，肖前军.曲线的基本向量组合成的曲线的曲率和挠率的计算［J］.湘潭师范学院学报（自然科学版），2005，27（4）：17-20.

［4］崔凤午.一般螺线曲率中心轨迹的曲率与挠率［J］.白城师范学院学报，2009，23（6）：1-4.

［5］华东师范大学数学系.数学分析（下册）［M］.北京：高等教育出版社，2001：146-148.

［6］王亚玲.维维安妮曲线的曲率、挠率及伏雷内公式［J］.长春师范学院学报，2012，31（3）：19-21.

The Calculation of the Curvature and the Torsion of the Curve of Implicit Function Form

HUANG Rui，CHU Yawei
（School of Mathematics and Statistics，Fuyang Teachers College，236037，Fuyang，Anhui，China）

Abstract：Implicit function theorem is applied to change the general equation of the plane curve and space curve into the form of unitary vector function in studying the curve of differential geometry，and this method is used to convert the calculation of curvature and torsion into the calculation of partial derivative of real function，and thereby，to conduct the curve research of the general equation.

Key words：implicit function theorem；curvature；torsion

作者简介：黄瑞（1985-），女，安徽阜阳人，硕士，助教，研究方向：微分几何.

基金项目：国家特色专业建设项目（TS11496）；安徽省质量工程项目

收稿日期：2015-09-08

中图分类号：O 186.1

文献标识码：C

文章编号：2095-0691（2016）01-0072-03