一种具有免赔额保单的保费估计与优化研究
邱美玲, 程丛电
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
一种具有免赔额保单的保费估计与优化研究
邱美玲, 程丛电
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
基于具有免赔额保单的重要性与最近庄小红等的一项工作,研究免赔额设置与保费厘定问题。从设置免赔额后总赔偿额不应减少的观点出发,建立一种新式赔偿方案(EPM)和一个表现承保人相关期望经济效益的数学模型(OPM)。在各次索赔额彼此独立且服从于同一对数正态分布和具有一定的以往赔偿记录的条件下,遵照方差相关原理,根据庄小红等工作中的有关结论,导出下年度应收取保费的极大似然估计。依靠所得估计,运用分析方法研究OPM,发展了优化承保人期望经济效益的一种方法。所建立的赔偿方案与所发展的优化方法可为承保人确定具有免赔额保单的免赔额度与保费额度提供一定的参考与依托。
保费; 赔偿; 期望经济效益; 极大似然估计; 统计优化; 误差界
0 引 言
保费是保险公司为履行一定的保险责任向投保人收取的实际金额。它的收取是保险公司正常运营的基础,其合理的定价对于公司的生存和发展至关重要。保费定价过低会使保险公司陷入经营困境甚至会导致破产,定价过高会使保险公司降低市场竞争力且会增加被保险人的负担,因此保费定价对保险公司来说是非常重要的精算问题.保费的厘定就是要求出一个适当保费,它不仅可以应付赔偿(理赔),而且还会使得保单组合的盈余足够快的增长.保费的厘定,对保险公司的生死存亡至关重要,因此合理的定价模式,一直备受保险工作者和理论界的广泛关注.
早在上世纪中叶国外就已有不少学者致力于保费定价方面的研究,例如,MICHAEL等[1](1978)与 RAVIV[2]讨论了保费定价问题。近20年来,国内关于该方面的研究发展较快。例如,1997年,谢志刚[3]研究了如何收取合理的保费,并决定合理的自留额和准备金数额,使公司保持良好的运作状态。2004年,陈飞跃[4]探讨了效用理论在保险实务中的4个应用。2006年,邓志民[5]建立与研究了一种投资收益下的保费定价模型。2011年,王桂胜等[6]探讨了在完全竞争的保险市场条件下如何制定最佳非寿险保费策略以促进公司的发展;王兵娜[7]提出了一种基于效用函数的无套利保险定价思想;温利民等[8]在指数保费原理下讨论了保费的经验厘定问题。2012年,魏艳华等[9]引入效用函数来描述决策者的风险态度,并讨论了效用理论在保险产品定价及确定最优投保方式中的应用。2013年,方颢等[10]考虑了具有广义FGM相依结构的复合泊松过程的Esscher定价泛函。2014年,张立东[11]探讨了将数据挖掘的建模、验证和使用4个环节集成于保险企业的定价系统之中的可行性;同年,彭俊杰[12]研究了数据挖掘技术在汽车保险理赔风险控制中的应用。
当前,大多数的保险险种中都涉及到免赔条款,免赔条款是保险人对保险理赔进行限制的一种方式,其主要思想是: 通过设置免赔额,减少一些频繁发生的小额赔付支出,提高被保险人的责任心和注意力,从而降低风险,同时也降低保险公司的经营成本。免赔额的确定与相关保费定价是既古老又新颖的实际问题与研究问题,不少专著有所论述,如BEWERE的风险理论[13]。1978年MICHAEL[1]等讨论了具有免赔条款的保险人保费定价策略。2014年庄小红等[14]研究了关于具有免赔额保单下年度保费的矩估计与极大似然估计并进行了数值模拟与相关探讨。
基于上述工作,并鉴于保险市场日益繁荣的实际状况,本文对关于具有免赔额的保单,提出一种新的理赔方案,并参考庄小红等的工作,在方差相关保费原理下,给出一种基于以往赔付记录预测下次应收取保费的极大似然估计。此外,本文还将建立一个表现公司期望经济效益的数学模型,并进行一定的优化研究。
1 模 型
1) 预测模型
关于一份具有免赔额b且年索赔额为随机变量X的保单,假设实际年赔偿额为
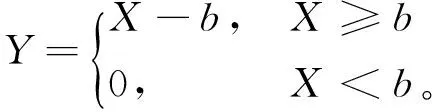
(1)
每年的索赔额Xi相互独立且服从于同一对数正态分布LN(μ,σ2)。文献[14]在观测到该保单前n年的索赔记录Y1,Y2,…,Yn,与方差相关保费原理,即第n+1年的保费为:Pn+1=E(Yn+1)+g(Var(Yn+1)),其中g(x)为[0,+∞]→[0,+∞]的单调连续递增函数,且g(0)=0的条件下,探讨了关于Pn+1的预测问题。鉴于该项工作和当前保险项目逐渐增多与繁荣,及合理的赔偿与收缴保费可以激发人们的投保热情,从而促进保险事业健康发展的观点,本文试进一步探讨下述保费预测问题EPM。
EPM:关于具有免赔额b且年索赔额为X的保单,假设实际年赔偿额为
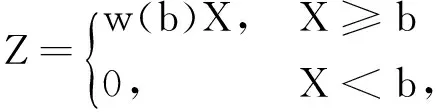
(2)
每年的索赔额Xi相互独立且服从于同一对数正态分布LN(μ,σ2),试在最近n次索赔记录Z1,Z2,…,Zn,与方差相关保费原理,即下年保费为:P=E(Z)+g(Var(Z)),其中g(x)为[0,+∞]→[0,+∞]的单调连续递增函数,且g(0)=0,的条件下探讨关于P的预测问题。

2) 优化模型

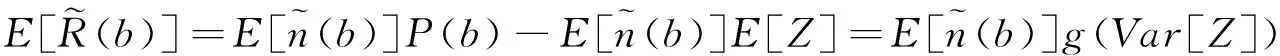


(3)
显然,寻求b使得R(b)最大形成一个优化问题,下面用OPM表示这一优化问题。依照统计优化的观点,对于该问题的研究可以帮助探索、寻找使得公司于该项目所获收入最大的免赔额b,从而优化公司的项目决策。
2 保费估计


定理1 关于问题EPM中的P的极大似然估计为
(4)
其中:
(5)
(6)
而
(7)
(8)
且
(9)

证明 易知
(10)
(11)
由式(10)与式(11)可得
(12)
另一方面
(13)
(14)
由式(13)与式(14)可得
(15)
最后,根据文献[14]知式(7),式(8)和式(9)成立;根据极大似然估计的不变性知式(4)成立;根据极大似然估计的不变性和式(12)与式(15)知式(5)与式(6)成立。综上,本定理正确。
3 优化研究
(16)

证明 易知存在i″使得xi″-1 证明 根据条件式(1)、式(2)和式(3)可得 由式(3), (17) (18) (19) (20) (21) 从而, (22) 本节汇报我们利用Mathlab对P(Z)的极大似然估计进行数值模拟结果。 表1 方差保费原理与标准差保费原理下极大似然估计的均方误差表 由表可见:随着样本容量n的增大均方误差递减趋近于0,这说明我们的方法对于大样本容量是有效的。 本文发展了一种新的免赔方案与一种表现承保人相关期望经济效益的数学模型,根据庄小红等最近的一项工作,在方差相关保费原理下,给出了一种基于以往赔偿记录预测下一年度应收保费的极大似然估计,并根据所建立的模型进行了一定的优化研究。改用其他方式预测该保险项目次年应收保费,在索赔额服从其他分布的条件下研究本文所讨论的问题,及探索更加先进的保险项目等是值得进一步考虑的问题。 [1]MICHAEL L S, GEORGE L H. Guidelines for insurers in pricing deductibles[J]. J Risk Insurance, 1978,45(2):217-238. [2]RAVIV A. The design of an optimal insurance policy[J]. Am Eco Rev, 1979,69(1):84-96. [3]谢志刚. 效用分析与保险定价决策研究[J]. 财经研究, 1997(8):27-31. [4]陈飞跃. 效用理伦在保险实务中的应用[J]. 中国保险管理干部学院学报, 2004(3):21-23. [5]邓志民. 投资收益下的保费定价模型[J]. 南开大学学报(自然科学版), 2006,39(6):95-97. [6]王桂胜,陈秉正.基于随机控制的非寿险保费定价策略[J]. 清华大学学报(自然科学版), 2011,51(6):827-830. [7]王兵娜. 基于效用函数的无套利保单定价模型[D]. 天津: 南开大学, 2011. [8]温利民, 吴贤毅. 指数保费原理下的经验厘定[J]. 中国科学:数学, 2011,41(10):861-876. [9]魏艳华,王丙参,孙春晓. 效用函数与保费定价原理[J]. 重庆文理学院学报(自然科学版), 2012,31(1):31-34. [10]方颢,王传玉,张大伟. 具有广义FGM相依结构的复合泊松过程的Esscher定价泛函[J]. 数学理论与应用, 2013,33(3):57-62. [11]张立东. 基于数据挖掘模型的车险保费个性化定价系统研究[D]. 秦皇岛: 燕山大学, 2014. [12]彭俊杰. 基于数据挖掘技术的汽车保险理赔风险控制研究[D]. 长春: 吉林大学, 2014. [13]BEWERE N L, GERBER H U, HICKMAN J C, et al. 风险理论[M]. 郑韫瑜,余跃年,译. 上海: 上海科学技术出版社, 1995:15-19. [14]庄小红,温利民,张溢. 方差相关保费原理下具有免赔额的保费估计[J]. 统计与决策, 2014(14):15-17. [15]ROSS S M. Stochastic processes[M]. New York: J Wiley, 1983. Cost estimation and optimization research for a new kind of deductible insurance QIUMeiling,CHENGCongdian, (School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China) The problems of setting up franchise and determining insurance premiums are studied based on the importance of insurance policy with franchise and the recent related work of ZHUANG Xiaohong et al. A new compensation scheme (EPM) and a mathematical model (OPM) which expresses the corresponding expected economic benefit of insurers are established from the viewpoint of total amount of compensation should not be reduced after setting up a franchise. Under the conditions that the amounts of insurance claims, which are all subject to a same lognormal distribution, are mutually independent and one has a certain past record of compensations, a maximum likelihood estimation on the premium of next year is derived based on the principle of correlation variance and the related conclusions in the work of ZHUANG Xiaohong et al. Further, an approach to optimize the expected economic benefits of insurers is developed by investigating the OPM analytically with the estimated premium of next year. The established compensation scheme and the developed optimization approach can provide references and suggestions for insurers to determine the franchise and premium of their insurance policy. premium; compensation; expected economic benefit; maximum likelihood estimation; statistical optimization; error bound 2015-09-14。 国家自然科学基金资助项目(11401393)。 邱美玲(1990-),女,辽宁凌源人,沈阳师范大学硕士研究生; 通信作者:程丛电(1966-),男,四川隆昌人,沈阳师范大学教授。 1673-5862(2016)01-0051-06 O212; O224;F840 A 10.3969/ j.issn.1673-5862.2016.01.012





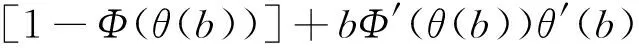




4 数值模拟


5 结 语

