基于利益相关者分析框架的房地产市场博弈均衡

文/柳翠连 华南理工大学广州学院 广东广州 510000



基于利益相关者分析框架的房地产市场博弈均衡

文/柳翠连 华南理工大学广州学院 广东广州 510000

【摘要】房地产市场有众多利益相关者参与其中，同老百姓的生活息息相关。本文从利益相关者视角出发，借助博弈模型对政府宏观调控政策的精准度进行分析，以期找出政府监管机构、地产商、购房者等利益相关方的博弈均衡关系，并分析宏观调控实效的成因。

【关键词】房地产；博弈；利益相关者

一、引言

我国政府从2003年开始进行了多番房地产市场宏观及中观调控，然而结果却不甚理想，房价在每次调控后都出现了不同程度的上涨。对此，业内的普遍从政策性失灵、供需结构性失衡、金融业与房地产业利益捆绑、居民购买力下降等方面进行讨论分析。但事实上，在房地产市场中各利益相关方对政府宏观调控着力点调控是否敏感、政府调控力度是否恰当及精准等问题的研究也十分必要。笔者将在下文通过构建房地产市场的博弈模型，从多个方面阐释调控失灵的主要原因并针对政府政策对房地产的影响进行重点分析说明。

二、房地产博弈因素与博弈结构

为探讨房市调控政策对各利益相关方的影响，有必要先理清这些相关方之间的关系。房地产市场的利益主体主要有四个，即政府（包括中央政府和地方政府）、开发商、银行（包括其他相关金融机构）、购房者。其中，开发商、银行、购房者（主要指投资性或投机性购房者）会从房价上涨中获益。政府在制定决策目标时要多重考虑利益方需要，既要拉动经济，又要服务民生，既要使自住型购房者以及未购房者从房价下跌中获益，又要平衡好经济发展与民生需要之间长远关系。

这些利益相关方都是这场博弈的参与人，他们的战略空间及相应的支付和信息集决定着最终的均衡，而从福祉经济学层面考虑，我们希望博弈的过程是一个帕累托改进的过程，最终的结果是一个增进社会福利的帕累托最优均衡结果，而实际上博弈的均衡具有多重性，即可能不止一个均衡解，最终的结果也可能由于参于人对其他参与人行动的预期不同而无法达成均衡，即便均衡达到，也未必是最优均衡。Kakutani不动点定理只告诉我们均衡的存在，却不能解决均衡的多重性困境。此外，房地产市场是一个高度信息不对称的市场，信息不完全也使房价长期以来在类似于无限期重复博弈中保持着向上的刚性，房市博弈中的大部分弱势参与人长期以来承受着较高的时间偏好率和负时间价值的威胁。这些理论上困境的现实意义是房地产市场博弈是极其复杂的过程，政府在调控房产市场时必须持有全局观念，全面统筹规划，进行合理的引导，向市场发送合理的预期信号，形成一致性预期，以期达成最优的均衡局面，这一决策理念必然和Aumann提出的“相关均衡”理论毫无二致。

三、房市利益主体的博弈行为分析

下文将应用抽象的经济数学模型来拟合现实中复杂的房地产市场，以期获得冰山一角的结论，以供探讨。

（一）政府机构对开发商的监督博弈模型

基于政府机构在房地产行业中的监督行为，这里先构造存在政府机构监督情况下开发商的行为选择模型。模型假设房产被开发后，政府可以获益t，政府对开发商的监督成本为S(t)，c表示开发商的合规成本，开发商按照政府的监管要求进行合规开发时，政府获益为C，若开发商出现不合规行为，则对社会损害为L，F为政府机构通过监督发现开发商不合规行为后对其进行的处罚。该模型的支付结构为{[监督，合规]-＞[C-S(t)，-c]}、{[监督，不合规]-＞[ C+F-S(t)，-c-F]}、{[不监督，合规]-＞[ C，-c]}、{[不监督，不合规]-＞[ -L，0]}。为考虑政策的动态性和信息的不完全，我们不分析纯策略而分析混合策略，我们用p代表政府监督机构检查的概率，q代表开发商合规的概率，求解该博弈的混合战略纳什均衡。给定q，政府监督机构的预期收益为：

q[C -S(t)]+(1-q)[C+F-S(t)]=qC+(1-q)(-L)

给定p地方政府的预期收益为：

p(-c)+(1-p)(-c)=p(-c-F)

联立上述两式可求得混合战略纳什均衡为：

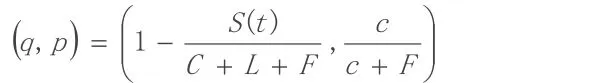
这表明，政府监察机构检查的概率以及开发商合规的概率受多个因素影响，主要包括该房产给政府所带来的收益C、监督成本S和处罚力度F这几个因素。根据上述均衡解，我们对此模型进行详细分析。

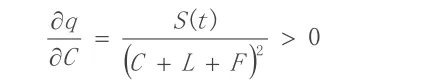
若上式说明政府从房产项目中获得的收益越高，则由于开发商不合规建设所造成的社会危害就越大。鉴于此，开发商只有更多地开发合规房产项目，才能有效降低对社会形成的负外部性，从而能够保证政府的收益不受影响。

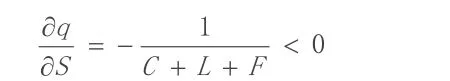
上式说明，S与q成反比例关系，即政府的监管成本越高，开发商合规开发房产的机率也就越低，一旦监管成本上升到一定额度，那么政府监管的支出将会大于收入，此时监查机构无法进行充分的监督检查，开发商就存在不合规的可能性。

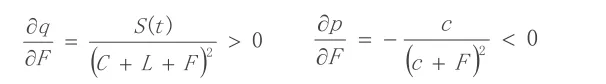
以上两式表明F降低之时，q随之减少，而p随之增大。这说明政府的处罚力度越低，对于开发商所形成的威慑力就越小，那么由于不合规开发所产生的风险效益会大大高于受到的处罚，这样开发商的不合规情况就有可能愈演愈烈；当F增大时，q将随之增大，而p将随之减小，这即意味着在威慑力较大的情况下，政府机构可以降低检查的必要性，同时提高开发商合规机率，但是如果只是毫无节制的提升惩罚力度，一旦开发商出现不合规行为就会造成巨大的经济损失，甚至血本无归，这时开发商就只能选择暂时性的不开发，这样房价就会因供给不足而呈现出一种虚高的态势。由此可见，有关惩罚力度F的探讨是值得考究的。

在上式中，c与p成正比例关系，两者同升同降，若开发商的合规成本越高，那么政府监管机构的检查概率也就越高。另一方面，由于政府监管力度的加大，开发商的合规成本也要随之加大，而合规成本的增加又会提升道德上的违规风险，那么这更要求政府要进一步加大监管督察力度。

通过上述分析可以得知，房地产行业是随时代的发展而不断发展变化的，政府不可固守陈规，要与时俱进、开拓进取，制定出符合市场实际情况的宏观调控政策，从而有效地引导和控制房地产走向更加经济的路径。

（二）政府机构对开发商的调控博弈模型

在开发商与政府的博弈之中，开发商可选高价或是低价作为策略，政府则可将维持或调控作为可选策略。假设开发商高价之时获取收益为P1，低价时收益为P2，且P1＞P2；如果政府对开发商行为进行调控，那么开发商需要付出C的成本；政府由增长带来的效用为E，房地产税费及土地出让金带来的收益为U，高价时的增长效用和房地产带来的税费收入比低价时更高，即E1＞E2，U1＞U2；若政府进行调控，则需付出I的成本，若高价时政府选择维持现有调控政策,则须承担地产泡沫破灭的风险R。调控模型该模型的支付结构为{[调控，高价]-＞[ E1+U1-I，P1-C]}、{[调控，低价]-＞[E2+U2-I，P2-C]}、{[维持，高价]-＞[E1+U1-R，P1]}、{[维持，低价]-＞[E2+U2，P2]}。从该模型可知，开发商的最优选择自然是房地产高价，此时博弈的均衡解是(高价，调控)或(高价，维持)；当I＞R时，政府会选择维持策略，博弈过程到此结束；而当 I＜R时，若政府和企业打交道是一次性的，则政府会选择调控，若政府和企业之间是一个重复博弈的过程，若在本次博弈政府选择调控，则房地产市场的发展可能变的较为平缓，这便会在一定程度上影响经济的增长，从而使政府的预期收益减少，进而影响下一轮博弈的收益支付，而事实上，政府和开发商的博弈必然是一个重复博弈，正的时间偏好率δ使政府陷入了一个进退维谷的两难困境。调控模型实质上表明了政府在调控房地产市场时，需要想方设法趋利避害，在经济与民生之间寻找最佳平衡点。

(三)开发商与购房者之间的博弈

开发商与消费者之间的博弈行为是房地产中最为显著的一种行为现象。为方便对此进行分析论述，我们可将购房者划分为“富人”（含投机性、投资性购房者）以及“穷人”（含自主需求类购房者、未购房者）这两种类型。购买者清楚自己经济状况，知道自己可以归结为哪种类型，而开发商却对购买者的经济状况一无所知，不知属于何种类型。假设房地产市场的活跃购买者是穷人的概率为q(0＜q＜1)，是富人的概率为(1-q)。消费者的支付函数为u=U(H,R)，H指房产所带来的效用满足，主要包括居住需求与投资需求两个方面。R指为了购买房产所需要支付的价格。开发商的支付函数为v=V(R,C)，R是收益函数，C是成本函数。高价房产和低价房产对应的开发成本分别为C2和C1(C2＞C1)；对应的收益分别为R2和R1(R2＞R1)；利润为P2和P1(P2＞P1)。假设H与R相互可以完全替代，那么穷人购买高价房产所得到的支付为-ΔR(Δ R=R2-R1＞0，因为穷人只要求低价房就得到完全的满足，而若购买了高价房则只能得到低价房的满足度，却做出了额外的支付)，购买低价房得到的支付为0。富人购买低价房产所得到的支付为-ΔR（富人需要高价房来使自己满足，若购买了低价房，则带来满足度的损失），购买高价房得到的支付为0。这样形成的不完全信息静态博弈格局的战略式表述为：对于开发商和穷人之间的博弈，{[高价，购买]-＞[P2，-ΔR]}、{[高价，不购买]-＞[-C2，-R1]}、{[低价，购买]-＞[0，P1]}、{[低价，不购买]-＞[-C1，-R1]}；对于开发商和富人之间的博弈，{[高价，购买]-＞[P2，0]}、{[高价，不购买]-＞[-C2,-R2]}、{[低价，购买]-＞[C1,-ΔR]}、{[低价，不购买]-＞[-C1,-R2]}；本模型对应的扩展式表述如下图的博弈树所示，开发商只有一个信息集，所以该模型是一个完全而不完美信息的静态博弈模型。

引入自然，根据图可的博弈树对上述博弈格局进行海萨尼转换，可得完全但不完美信息博弈，再将不完美信息博弈转化为等价的策略型博弈。可得到对应的扩充博弈格局。该博弈具有如下贝叶斯均衡解：

①富人：{[买，买]，高价}，如果R2≤2R1

②穷人：{[买，买]，高价}，如果R2＞2R1 且(1-q) ΔR-ΔC＞0

博弈均衡要求ΔR/ΔC≥1/(1-q)条件成立，这是利润函数在离散型条件下的结论，推广到连续的情况下，可以得到dR/dC≥1/(1-q)＞l条件成立，根据厂商理论可知，在充分竞争条件下有MR=MC，所以有MR/MC=dR/dC=l成立。由这些成立式可知作为非完全竞争的重要表现形式之一，房地产市场需要对开发商的边际利润以及居住需求的相对价格进行调整降低，这样才能够激发穷人购房欲望，才能有效改善社会的整体福祉。鉴于此，政府部门要尽可能地发挥在市场中的因势利导作用，采用多种方式来引导开发商根据市场实际情况制定合理的房价，与此同时，政府还要确保保障性住房的数量，通市场手段来引导房价回归合理区间。

参考文献

[1]Aumann, R, 1974. Subjectivity and Correlation in Randomized Strategies. Journal of Mathematical Economics,1:67-96.

[2]于维生,朴正爱.博弈论及其在经济管理中的应[M],清华大学出版社,2005.

[3]张维迎.博弈论与信息经济学[M],上海三联书店,1996:110-112.