桥梁流固耦合研究现状及进展

黎　亮，曾　勇

(贵州省交通规划勘察设计研究院股份有限公司， 贵阳　550081)



桥梁流固耦合研究现状及进展

黎亮，曾勇

(贵州省交通规划勘察设计研究院股份有限公司， 贵阳550081)

摘要：对目前桥梁流固耦合的分析方法和研究成果进行总结和评述，指出现有研究中存在的问题，为进一步深入研究提供参考。

关键词：流水压力；水浮力；流固耦合；地震响应

在如地震、山洪等动力作用下，水中的桥梁结构会产生一定振动和变形，致使周围水体产生振动；而振荡的水体会产生动水压强，其对桥梁结构产生作用，欲改变桥梁结构的运动状态。这种作用与反作用即为流固耦合效应，其会自始至终贯穿整个外动力作用过程[1]。流固耦合效应改变了桥梁本身的动力特性，加深了桥梁在外动力作用下的响应复杂程度。

流固耦合作为多学科综合问题的一个典型代表，其涉及固体力学、振动力学和流体力学，是两相物理介质之间的相互作用。本文对于流固耦合的研究，主要从2个角度出发，一是试验分析，二是理论研究。

1试验分析

2006年，赖伟[2]进行了水下桩基础桥墩的振动台试验研究，分析了桥梁桩基础桥墩在受到地震动力的过程中，动水压力对结构的影响程度。试验结果表明，流固耦合现象的产生与流体水的存在有关，其改变了结构的动力特性和地震动响应。2010年，杨吉新[3]对水中结构的振动特性进行了试验研究，其将3组不同尺寸的试件置于不同水深的试验水槽内，分别应用共振法和模态法对试件进行了动力特性测试，详细列出了试验步骤和所得结果，阐述了水深对悬臂结构振动特性的作用，指出随着水位深度变化，结构固有频率的变化程度逐渐增大，刚度较小的结构，其固有频率随水位的升高，受水的阻尼影响较大。

2理论研究

理论上，流固耦合的研究始于1933年。其时，H.W.westergaard[4]初次对水体-重力坝体系的动水压力进行研究。之后，大量学者对流固耦合相关问题进行了研究，如水库与坝体的相互作用、舰船运动、水工闸门振动、海岸工程、储液罐振动、水中球壳的振动等。Landweber L.、Liaw C Y.、李玉成等人[5-7]分别于1967年、1974年、1993年探索了流体-结构之间的相互作用，认为流体对结构动力特性的影响较大。所以，对水下结构进行动力分析时，要考虑结构-水的耦合效应。

流固耦合作用的分析方法大致分为3类：附加质量法、有限单元法、混合法。附加质量法属于解析法，有限单元法属于数值分析法，混合法是这2种方法的混合体。

2.1附加质量法(解析法)

附加质量法[8]是假设一定质量的水和结构一起运动，故这部分水的惯性力和水中结构物表面的实际动水压力相等。该方法的优点是物理意义明确、形式简单。大量研究认为，结构振动时水体会产生波浪，而波浪主要产生以下3种载荷，即惯性力、绕射力和拖曳力。对于面积大、尺寸大的结构，波浪的绕射力和惯性力是其主要分量；对于小尺度结构，波浪的惯性力和拖曳力是其主要分量。因此，在水工结构物中，对应于大面积刚度较大的结构物，如拱坝，一般较多使用Westergaard公式；而在现有桥梁结构研究中，对应的是横向尺寸较小的结构，如墩柱桩基，故通常使用Morison公式和它的修正公式。

2.1.1Westergaard公式

水下结构多以大面积的结构形式存在，且刚度较大。因此，Westergaard公式虽将坝体假设为刚体，仅考虑水体的动水压力，但在模拟坝体的流固耦合上，有较高精度，其解至今仍为许多国家坝工抗震设计规范所用。

Westergaard公式可分析垂直刚性坝面在地面水平简谐运动时的动水压力。坝面最大动水压力沿坝高呈抛物线变化[9]，即

(1)

(2)

式(1)中，参数C可根据效应相等原理求出，如坝体动水压力相等、总剪力相等、最大弯矩相等。根据最大弯矩相等求得的平均动水压力公式如下：

(3)

因为坝面动水压力的性质与惯性力的性质类似，即坝面动水压力的大小与加速度成正比，方向与加速度相反，故动水压力可用坝面一定质量的水体惯性力来替代。若将附加水体质量的宽度设为m(y)，则根据附加水体的惯性力同动水压力相等的条件：

αγwm(y)=p(y)

(4)

可解得

(5)

将水的容重γw=0.031 25ton-ft-3和式(3)代入式(5)，即可得出著名的Westergaard附加质量公式：

(6)

2.1.2Morison公式

在现有关于桥梁结构的研究中，研究对象多是墩柱桩基类横向尺寸较小的结构，较多使用Morison公式及其修正公式。该公式可表明水对柱体的影响是由作用于结构上的惯性力和粘性阻力组成[10]：

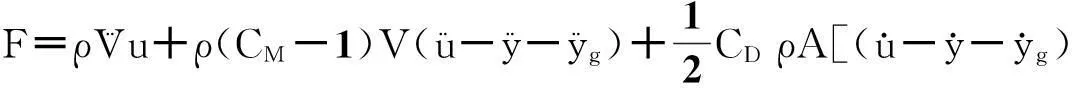
(7)

由式(7)可以明显看出，应用Morison公式计算动水压力时，2个水动力系数—等效惯性力系数CM和等效阻尼力系数CD的选取不同，得出的动水压力值也不同，且差别很大。水动力系数取值是应用Morison公式的关键，是研究Morison公式的重点。1998年，马良[11]应用量纲分析法，研究Morison方程中曳力系数CD与雷诺数Re的关系。同年，李玉成[12]研究了环境条件对水动力系数的影响，得到归一化的水动力系数。

2.2有限单元法(数值分析法)

有限单元法即是依据有限元理论，分别构建符合结构运动特征的结构运动方程、符合流体运动状态的流体运动方程，以及流固耦合的边界条件，并通过数值分析方法求解结构效应。

Zienkiewicz[13]给出了有限元求解流固耦合作用问题的一般格式。根据不同的目标函数，有限单元法可分为拉格朗日法和欧拉法2大类。拉格朗日法将流体域假定为弹性体，可在流体-结构结合面的位置较好地描述物质结构边界运动的轨迹。欧拉法在描述流体波动时，可选择相同的位势函数。同时，划分流体单元网格所采用的位移单元离散法可使得流场网格单元单独存在，以此保证求解过程中，网格位置可根据设定的参数进行调整。拉格朗日法重点关注质点，方便追踪结构运动；而重点关注空间坐标系的欧拉法则更适合于描述流体的运动。2种方法运动描述方式不同，其所采用的坐标参照系也不同。Nor、Hirt[14]、蒋莉[15]等提出了任意拉格朗日—欧拉法，其可以很好地解决流体与结构相互作用问题。任意拉格朗日—欧拉法以欧拉法、拉格朗日法为基点，并综合了两者的优点。其用于流体域分析时，网格点按照自由流体表面的运动或结构与流体接触面的运动变化，且该计算方法考虑了运动边界的非线性效应。任意拉格朗日—欧拉法对于解决大变形、非线性的问题非常适用。

2.3混合法(半解析半数值法)

Westergaard公式及Morison公式均具有适用性，但桥梁分析多采用Morison公式。然而Morison公式由于水动力系数的变异性而使得计算结果存在不确定性。在对动荷载影响下的水下墩柱动水压力研究过程中，赖伟[16-18]主要在寻求一种半解析半数值的方法来分析流体与固体之间的相互作用。2007年，他基于地震下弹性矩形空心桥墩上的水动力，提出了一个新的半解析半数值方法，即利用特征函数扩展法，采用线性辐射波浪理论来分析空心墩内部和外部水体作用于桥墩有限个作用节点上的动水力，得到矩形空心墩桥梁结构与水耦合振动的运动方程。2010年，他依据线性势波理论，描述了水中截断圆柱体作水平、竖向简谐运动时固体结构周边的辐射波浪。另外，他还利用分离变量法，分别得出含有未知常数的3个流体子域速度势的简谐表达式，并采取比较简单的匹配方法，使流体子域的共同边界满足压力和法向速度的连续条件，从而得到速度势，并进一步获得由等效附加质量和附加阻尼表示的柱体侧面、柱体、下表面的动水力。2014年，他通过Trefftz完备函数求得了流体控制方程的解，并通过有限单元法解得耦联运动方程。同年，他还基于流体速度势理论研究了水中桩基圆形承台作水平简谐运动时承台侧面的动水压力，并提出一个计算桩基圆形承台侧面动水压力的半解析半数值方法，由此得出一个新的附加质量系数。

3研究评述

通过上述对桥梁流固耦合的试验分析及实例研究，得出如下结论。

1) 流固耦合现象的产生和流体水的存在有关，其改变了结构的动力特性和地震动响应。

2) 在考虑流固耦合作用的动力分析中，水体对结构自振频率有一定影响，自振频率随水位升高而减小，且水位越高，自振频率减小速率越大。

3) 桥梁分析多采用Morison公式，而水动力系数取值是应用Morison公式的关键，是研究Morison公式的重点，故须予以重视。

4目前存在的问题

目前对桥梁流固耦合的研究仍不够系统和充分，主要体现在以下方面。

1) 由于流固耦合问题的复杂性，影响因素很多，很难进行综合性的全面考虑，一般需对其作一定假设，模型也需简化。

2) 目前，对于流固耦合作用而言，理论上还有有限单元法及半解析法。由于拱结构的特殊性，目前尚无成熟的研究理论，故应结合试件模型的试验研究进一步分析，以提高研究的可靠度。

5结束语

流固耦合问题复杂，影响因素很多，很难对其进行综合性的全面考虑。分析时一般需对其作一定假设，模型也需简化。静力分析时，由流水速度产生的侧向流水压力、桥墩淹没引起的竖向水浮力是桥梁静力响应的主要影响因素。为确保桥梁安全，准确评价其动力响应性能，对桥梁流固耦合作用下的结构行为进行系统的研究十分必要。

参 考 文 献

[1]WILSON J F.海洋结构动力学[M].杨国金，郭毅，唐钦满，等译.北京：石油工业出版社，1991.

[2]赖伟，王君杰，韦晓，等.桥墩地震动水效应的水下振动台试验研究[J].地震工程与工程振动，2006，26(6)：164-171.

[3]杨吉新，秦延飞，刘素云，等.水中结构振动特性的实验研究[J].武汉理工大学学报(交通科学与工程版)，2010，34(6)：1104-1107.

[4] WESTERGARRD H M.Water Pressures on Dams during Earthquakes[J].Transactions of ASCE，1933，98(2)：418-433.

[5]LANDWEBER L.Vibration of a flexible cylinder in a fluid[J].ship research，1967(11)：143 -150.

[6]LIAW C Y，CHOPRA A K. Dynamics of surrounded by water [J].Earthquake Structure. Dynamics, 2014，18(3)：32-33.

[7]李玉成，滕斌.波浪对海上建筑物的作用[M].北京：海洋出版社，1993.

[8]童予靖，刘正兴.流固耦合问题中的附连水质量研究[J].上海力学，2013，18(4)：312-320.

[9]傅作新.结构与水体的相互作用问题[J].水利水运科学研究，2012(2)：104-119.

[10]MORISON J R，O＇BRIEN M P，JOHNSON J W，et al.The force exerted to surface wave on piles[J].Petroleum Transaction，1950，2(5)：149-154.

[11]马良.对莫里森方程中曳力系数CD浅析[J].中国海洋平台，1998(3)：16-18.

[12]李玉成.Morison方程水动力系数归一化的探讨[J].水动力学研究与进展，1998(3): 329-337.

[13]ZIENKIEWICZ O C.The Finite Element Method[M].London：Mc Graw-Hill，1977.

[14]HIRT C W，AMSDEN A A，COOK J L.An arbitrary Lagarangian-Eulerian computing method for all flow speeds[J].Computation Physics，1974(14)：227-253.

[15]蒋莉，沈孟育.求解流体与结构相互作用问题的ALE有限元体积方法[J].水动力学研究与进展，2000(6)：148-155.

[16]赖伟，王君杰，胡世德.地震下桥墩动水压力分析[J].同济大学学报(自然科学版)，2014，32(1)：1-5.

[17]赖伟，谢凌志，高永昭.矩形空心墩地震动水效应的求解[J].四川建筑科学研究，2007，33(增)：67-71.

[18]赖伟，陈述清，吴东.沿竖向运动的水中截断圆柱体辐射波浪问题的解析解答[J].四川建筑科学研究，2010，36(3)：56-60.

Status Quo and Development of Research on Fluid-solid Coupling of Bridges

LI Liang, ZENG Yong

Abstract:This paper summarizes and reviews analysis methods and research achievements of fluid-solid coupling of bridges at present, and points out the problems in current research to provide a reference for further deep research.

Keywords:flowing water pressure; water buoyancy; fluid-solid coupling; seismic response

文章编号：1009-6477(2016)01-0057-04

中图分类号：U441+.2

文献标识码：A

作者简介：黎亮(1990-)，男，湖南省岳阳市人，硕士，助工。

收稿日期：2015-10-08

DOI:10.13607/j.cnki.gljt.2016.01.013