考虑风能随机性的V S C - H V D C风电并网优化方法研究

于永生，冯延晖，江红鑫，邱颖宁（南京理工大学能源与动力工程学院，江苏南京　210094）



考虑风能随机性的V S C - H V D C风电并网优化方法研究

于永生，冯延晖，江红鑫，邱颖宁
（南京理工大学能源与动力工程学院，江苏南京210094）

KEY W0RDS：VSC-HVDC；wind farm；genetic a1gorithm；simP1ex method；random wind

摘要：随着能源危机的日益临近和电力电子器件技术的大幅进步与应用，风电场经VSC-HVDC并网已经变成了一种可能。相对于其他诸如火力发电和水利发电等传统发电方式，风力发电不能够控制能量的注入与供给，所以风力发电的输出稳定与否主要取决于风速的变化。建立了风电场等效聚合模型和柔性直流输电（VSC-HVDC）的详细模型。为了平抑风电并网时风电场的功率波动，分别采用了单纯形法和遗传算法对柔性直流输电的控制器进行了优化，优化结果显示，两种优化方法均能平抑风电场的输出功率波动。

关键词：柔性直流输电；风电场；遗传算法；单纯形法；随机风

以风力发电为代表的新能源发电技术与传统的发电型式如火力发电的区别之一就是能量来源的不可控性，这就造成了风电场出力的不稳定性，表现在风电场输出功率稳定性的好坏取决于风能资源的稳定与否。基于IGBT的新型输电方式——柔性直流输电，以其高度可控性得到了风电并网领域内众多专家学者和工程师广泛关注[1]。

文献[2]对于采用双馈机组的风电场经柔性直流输电并网设计了一种新型控制方式，并通过风电场波动和负荷波动进行仿真验证该控制方式的正确性。文献[3]对柔性直流输电的风电场侧变流器设计了一种新的交流电压—功角控制方式，能够实现对波动风速的同步传送。文献[4]对于两端VSC-HVDC采用单纯形算法进行了优化，仿真结果显示单纯形算法对于VSC-HVDC优化有重要的作用，但该文所做研究是基于间接电流控制。间接电流控制动态响应慢，工程实际大多采用响应速度快、鲁棒性好的直接电流控制。文献[5]采用遗传算法对柔性直流输电控制器参数进行优化，优化后的系统响应特性较优化前有较明显改善。文献[6]采用单纯性法对风电场经多端柔性直流输电进行了优化，但文献[6]仅考虑到了稳态情况下的响应情况，并没有对随机风况下的柔性直流输电模型进行分析讨论。

鉴于大多数文献都没有涉及到风电场和柔性直流输电系统之间的相互作用，考虑到随机风速，即风速随机变化情况下风电场的输出特性，本文对于风电场在随机风条件下输出特性进行了讨论，并采用遗传算法和单纯形法两种启发式优化算法分别对柔性直流输电控制器参数进行了优化，最后将2种优化方法的优化结果进行了比较分析。

1　风电场模型

由于技术的限制和风力发电的特性，与其他传统的大型发电机组不同，风机的单机容量目前最大只有几个MW，一个风电场中风力发电机组数量众多，从几十台到上百台不等，如果所有风力发电机均采用发电机的全暂态模型来仿真，这样的仿真模型是一种很复杂的高阶模型[10]。仿真分析时，计算时间长，内存需求大，对计算机的配置要求较高。事实上，研究某个风电场对电力系统的影响，可以将整个风电场看作一个整体，并不需要考虑每一台风力发电机对电网的影响。因此在大规模风电场并网仿真计算中，不适合也没有必要采用详细模型来研究整个风电场对电网的动态性能的影响。研究电网和风电场通过输电系统之间的交互作用，可以将相同类型的风力发电机等效为一台机组[10-11]。对于有上百台机组的风电场，并网分析中采用这种聚合模型是很有必要的。在对于含风电场的电力系统暂态分析时，可以通过这种化简等值，降低仿真模型阶数，节约计算时间[13]。

将风电场等效为一台发电机的仿真方法的精度虽然略低于将风电场所有发电机的数学模型全部代入仿真模型中，但这种等效的方法仍然可以正确反映整个风电场在并网点的动态特性，显著减少了计算时间，具有很高的实用性[12]。本文将风电场等效为同一个聚合模型，风电场的聚合模型包含了风速模型，风力机的机械部分，等效的机组、母线、变压器等电气元件和等效风速[12]。引入等效风速是为了研究风能资源的特性对于风电场并网功率的影响。

对于等效风速的计算方法，文献[12]将整个风场机组功率求取平均值后，通过等效风功率曲线逆函数求取等效风速。

风力机模型

式中：Pw为风轮从风中捕获的风能；p为空气密度，kg/m3；CP为风力机的风能转换效率系数；AR为风轮扫过的面积；vw为风速，m/s；λ为叶尖速比；β为叶片桨距角，°。

目前风力发电的研究主要采用风速的四分量模型[21]。为了准确地模拟风电场风速对风电场出力的影响，以欧洲某个风电场的风速统计为基准，按四分量模型进行拟合，得到一个风速的随机数序列，作为风电场风速输入。

考虑到风电场需要能够反映风电场风机出力变化对风电场输出功率的影响，本文用一台大容量风力发电机来代表整个风电场的出力状况[10]。该等值机组在等效风速作用下所产生的风电功率与所有机组输出功率相等。等效风力发电机采用直驱型永磁同步发电机（PMSG）。由于实际中风力机转速很慢，需要安装齿轮箱等变速环节。本文主要研究风电场风速变化对风电场输出的影响，为了简化，本文省略了齿轮箱环节，即风力机中齿轮变比为1。风力发电机的极对数设置为100，此时在额定恒风速下运行风力发电机输出电压和电流频率为50 Hz。变流器和风电场以及变流器和电网之间的联结处含有等效变压器以及联结电抗和等效电阻。

风电场模型如图1所示，四分量风速模型输出为风速。风力机模型输入为风速和永磁同步发电机的转速，输出为转矩。风力机桨距角控制模型用来调节风力机的桨距角。

2　柔性直流输电模型

2.1换流器数学模型及其控制模型

目前工程上投入应用较多的柔性直流输电（VSC-HVDC）主要采用三相两电平结构[8]。

由Kirchhoff定律，可得如下暂态方程

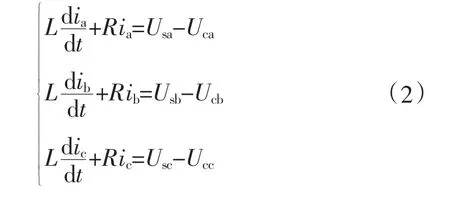
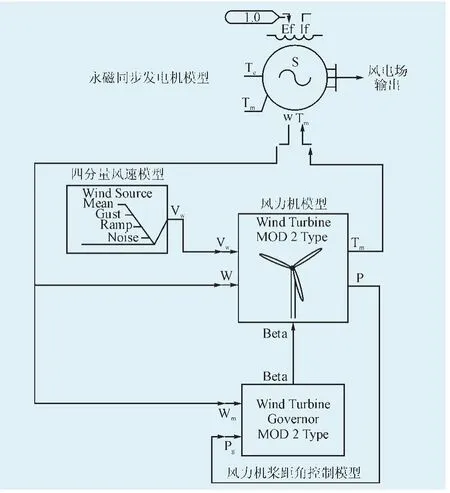
图1　PSCAD中的风电场模型Flg. 1 Wlnd farm model ln PSCAD

图2　柔性直流输电换流站模型Flg. 2 VSC-HVDC system dlagram

式中：ia，ib，ic为三相电流；Usa，Usb，Usc为风电场变压器一次侧三相电压；Uca，Ucb，Ucc为变流器交流侧基波三相电压。式（2）经过dq变换后为：

直流侧动态方程：

式中：ir为电容和变流器之间直流线路的电流；iL为电容右侧直流线路的电流；Ur为直流电压，该公式描述直流电容流入流出电流与电容电压的关系。

根据瞬时无功功率理论[8]，abc三相静止坐标系下换流站与交流系统交换的有功功率ps和无功功率qs为：

经过dq变换，在旋转坐标系中，风电场输出的有功功率ps和无功功率qs为：

当d轴以电网电压向量定位时，即Usq＝0，则式（6）变为

在式（7）中，分别控制id和iq可以调节换流站与交流系统交换的有功和无功功率。

对于直接电流控制，令：

又有

当标量函数V.L＜0时，系统处在稳定平衡点，ur能够跟踪urref，因此可以得出控制公式：

即为：

在大多数情况下，u.rref＝0，即可得到直流电压PI控制器。同理可以推导出其他控制量的控制器。

采用前馈解耦控制，可以得到电网侧换流站（G-VSC）的电流内环控制和风电场侧换流站（WFVSC）的电流内环控制。为了减小风电场侧换流站输出波动，风电场侧换流站采用改进的电流内环控制[17]。

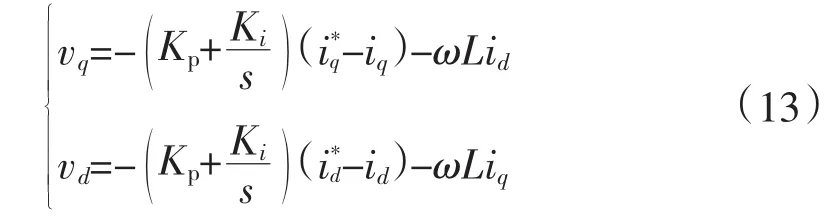
图3　风电场侧电流内环控制Flg. 3 Inner current control of the WF-VSC

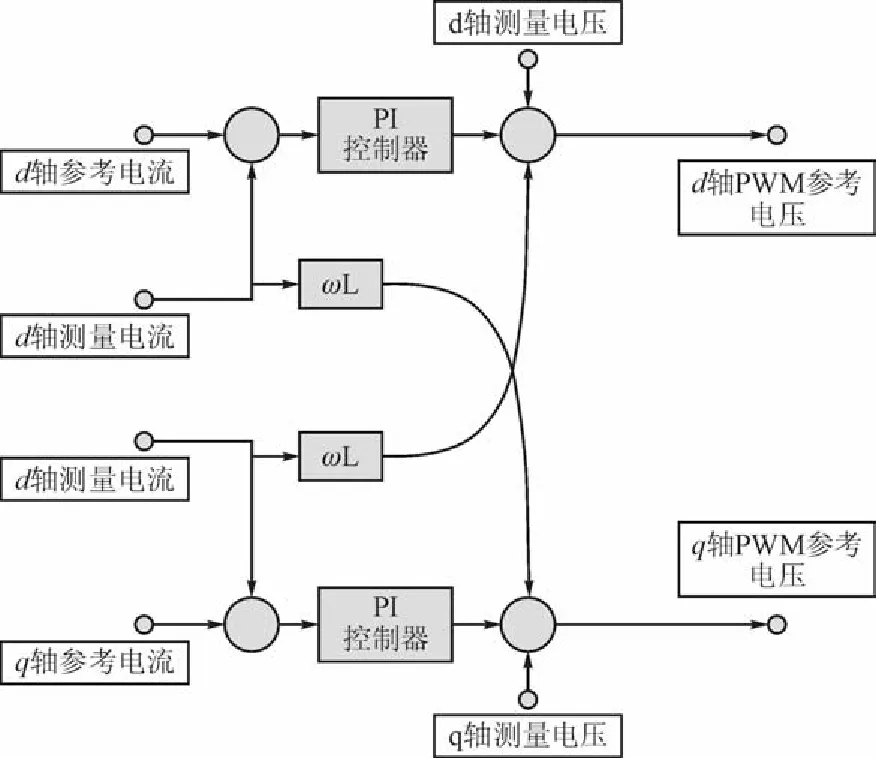
图4　电网侧电流内环控制Flg. 4 Inner current control of G-VSC

内环电流控制的传递函数[19]为：

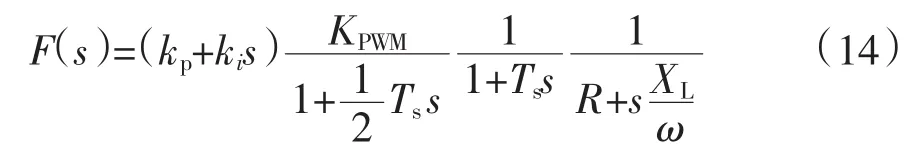
式中：（kP＋kis）为比例积分环节；1/（R＋sXL/ω）为等效电感和电阻的传递函数；KPWM/（1＋（1/2）Tss）为变流器传递函数；KPWM为PWM的等效增益，KPWM＝Udc/（2urms），urms为交流线电压有效值。1/（1＋Tss）为采样滤波环节。

本文所采用模型通过外环控制来区别不同换流站的控制职能。在连接有风电场的多端系统中，由于风电场无法提供一个稳定的电压，所以离线仿真时需要大电网先并入网络给柔性直流输电系统提供一个稳定的直流电压，然后风电场才能并入网络，否则容易引起风电场输出的波动[7]。

图5　外环电压控制器Flg. 5 Voltage outer control

外环电压控制的传递函数[19]为：

式中：（kP＋kis）为比例积分环节；1/（1＋Tss）为采样滤波环节；usq为交流侧三相电压经dq变换得到的q轴电压；Udc为直流电压；C为直流侧电容；1/（1＋3Tss）为电流内环的等效传递函数。

图6　外环有功控制器Flg. 6 Actlve power outer control

图7　外环无功控制器Flg. 7 Reactlve power outer control

外环有功和无功的传递函数[19]为：

式中：（kP＋kis）为比例积分环节；1/（1＋Tss）为采样滤波环节；usq为交流侧三相电压经dq变换得到的q轴电压；Udc为直流电压，1/（1＋3Tss）为电流内环的等效传递函数。

2.2电缆线路模型

电缆线路暂态模型[20]如图8所示。

图8　电缆线路的分布模型Flg. 8 Dlstrlbutlon model of the cable llne

式（22）为电缆线路的微分方程组。由于该方程组在电缆线路中很难找到解析解。在含有多导体的同轴电缆中，这个模型会更加复杂。因此，大多数情况下主要采用行波模型。行波模型如式（23）所示。其中ω为输电线传输正弦波角频率，χ和t分别为传播距离和时间。

省略对时间的导数，可以得到仅关于距离χ的微分方程组：

令Z0＝R0＋jωL0，Y0＝G0＋jωC0。对于含多导体的同轴电缆来说：

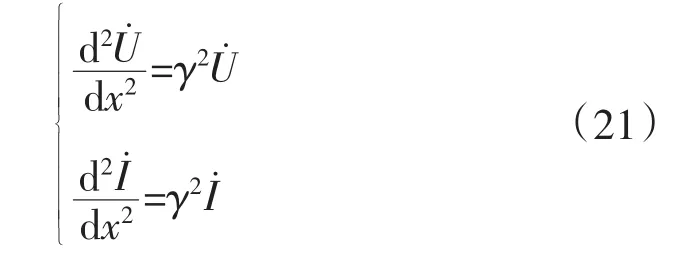
该方程的通解即为行波模型：

由于直流线路不同于交流线路，直流线路没有基波频率ω，所以为了降低模型的复杂度，电缆线路模型采用Bergeron模型，Bergeron模型基于行波理论，Bergeron是一连串π形等效电路，该模型能够准确反映电缆线路的电感和电容的分布特性。Bergeron模型的电阻参数基于半集总模型，电阻值有50%集中在电缆中心点，另外两端各占25%的阻值。

表1　电缆线路参数Tab. 1 Cable parameters

3　单纯形法

假设搜索空间中有m个点，每个点包括d个分量，记X＝｛χ1，χ2，…，χd｝，其中m＝d＋l。将m个顶点按照其对应的目标函数值从小到大排序（优劣排序），第i个顶点记作Xm，i，m个顶点的单纯形Sm表示为：S＝｛Xm，1，Xm，2，…，Xm，m｝。单纯形Sm的最差顶点记为Xm，w，Xm，w＝Xm，m；最好顶点记作Xm，b，Xm，b＝Xm，1；除最差顶点Xm，w之外的其他所有顶点的形心记作Xcm，w；除第i个顶点Xm，i之外的其他所有顶点的形心记作Xcm，i。

单纯形法的搜索步骤为：

1）给定初始顶点＝X＇m，0＝[χ0，1，χ0，2，…，χ0，m-1]

则单纯形其他初始顶点为：

2）a）检查收敛准则，若满足则终止优化。b）计算各顶点的目标函数，根据目标函数值从小到大顺序排序（优劣顺序）。排序后各顶点依次为Xm，1，Xm，2，…，Xm，m；确定最好顶点Xm，b、最差顶点Xm，w，计算形心设置一次成功搜索标志变量F1ag＝F。

3）单纯法寻优过程：

a）X*＝Xm，w；F1ag＝F；

b）计算反射点

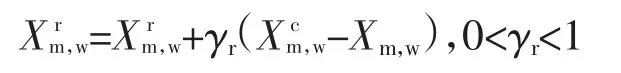
及其对应的目标函数之f（Xrm，w）；

c）如果f（Xrm，w）＜f（Xm，b），则计算扩张点

及其目标函数值f（Xem，w），

如果f（Xem，w）＜f（Xm，b），则

否则X*＝Xrm，w；

d）如果f（Xrm，w）＜f（Xm，m-1），则

e）如果

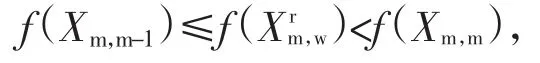
则计算内压缩点

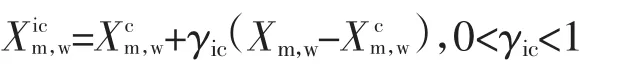
及其目标函数f（Xicm，w），

如果f（Xicm，w）＜f（Xm，m），则

否则X*＝Xrm，w；

f）如果f（Xrm，w）≥f（Xm，m），

则计算外部压缩点

及其目标函数值f（Xocm，w）；如果

则X*＝Xocm，w，F1ag＝T；

g）返回计算结果F1ag和X*；

4）if（F1ag＝T）｛Xm，w＝X*；Goto（2）｝

e1se｛

a）单纯性各顶点以最好顶点Xm，b为中心进行整体压缩，即

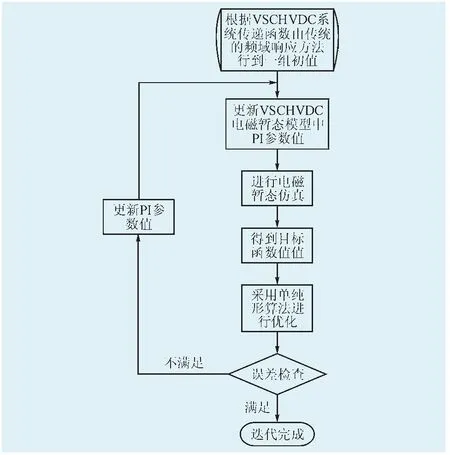
图9　单纯形法优化过程流程图Flg. 9 Flowchart of the slmplex method

b）Goto（2）

｝

由于目标函数是个具有凸性的超平面，故它的一个最优值（若存在的话）必在单纯形的某个顶点上得到[14]。

4　遗传算法

遗传算法作为一种启发式算法，模拟“物竞天择，适者生存”的生物进化理论，通过维护一个包含潜在解的群体执行多方向的搜索。遗传算法的步骤如下[16]：

1）对优化问题的解进行编码。按生物学术语，我们称一个解的编码为一个染色体，组成编码的元素成为基因。

2）适应度函数的构造和应用，适应度函数一般是依据优化问题的目标函数而定。适度函数对应于生物学中的环境，适度函数是用来淘汰掉劣等基因，即不满足适度函数的染色体将被淘汰掉。

3）（随机）产生初始种群并计算各染色体的适应度。

4）父母双亲的选择。衡量标准就是染色体的适应度。从生物学的角度讲，后代具有优良特性的先决条件是选出的双亲具有相对优良的特性。不满足给定条件的个体不能作为下一代的双亲，即被淘汰。

5）繁衍后代。应遵循两条自然法则：父母的优良特性得以遗传、后代能够产生新的优良特性。这可通过交叉和变异的协同作用来实现。

6）群体的换代。重复第4，5步直到新的群体全部产生，并计算各染色体的适应度。

7）进化过程终止判别。依据某种收敛准则进行判断，该收敛准则可以以目标函数的误差值，也可以用固定代数作为判别条件。如果满足则终止进化，否则重复第4～7步进行下一轮迭代。

本文所采用的遗传的参数为：群体规模为100，交叉率为0.8，变异率为0.1，选择方式为随机选择，以40代作为收敛依据。

遗传算法并不能保证获得问题的最优解，但是使用遗传算法的最大优点在于你不必去了解和操心如何去寻找最优解。而只要简单地淘汰掉一些表现不好的个体就行了。这样，经过若干次淘汰，剩下的个体即为满足条件的优良个体。

5　仿真结果与分析

由ITAE最小化准则[15]，本文设置优化系统的目标函数为：

式中：eP_rec为海上换流站（整流侧）有功功率给定值与测量值之间的差值；eP_inv为陆上换流站（逆变侧）有功功率给定值与测量值之间的差值；eUdc为直流侧电压给定值与测量值之间的差值。

由图10和图11我们可以看出柔性直流输电输送功率在趋势上跟随风速变化。由于风速的大幅波动导致能量来源的大幅波动，不可能使得风电场的输出波动为零。本文所做工作即在风速随机变化的情况下使得柔性直流输电的功率波动尽量减小。

图10　风速Flg. 10 Wlnd speed

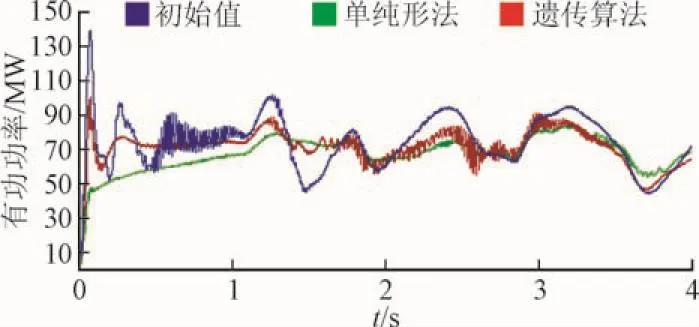
图11　风电场侧有功功率Flg. 11 The actlve power ln WF-VSC

由图11可以看出，在系统启动阶段，采用遗传算法优化的控制器能够使得整个系统的响应速度优于单纯形法的优化结果。系统启动阶段的最大超调量98.254小于系统初始值运行状态下的最大超调量139.463。而单纯形算法优化后的结果没有超调量，属于过阻尼系统，响应速度太慢。同时，采用遗传算法优化后的控制器输出功率在0.562 s后即接近风电场的额定功率75 MW，而采用单纯形法优化后的控制器则需要在1.373 s后才接近风电场的额定输出功率。

采用初始参数的控制器，柔性直流输电整流侧输入功率1～3 s之间有功功率标准差为13.316 7。整流侧控制器采用单纯形优化后，整流侧输入功率1～3 s之间有功功率标准差为4.451 7。整流侧控制器采用遗传算法优化后，整流侧输入功率1～3 s之间有功功率标准差为9.357。

由于柔性直流输电逆变侧控制柔性直流输电直流侧电压，因此在系统启动阶段，交流侧会向直流侧输送大量的有功功率，如图12所示。此时的初始控制器参数下的反向功率超调量达到367.278 MW。该反向超调量可以通过增设柔性直流输电启动电阻来消除，该问题不在本文讨论范围。

图12　逆变侧有功功率Flg. 12 The actlve power ln G-VSC

由图12可以看出，在系统启动阶段，采用遗传算法优化的系统的响应与单纯形类似，但系统的稳态误差要比单纯形小，而在超调量指标遗传算法要小于控制系统初始参数的动态性能。

采用初始参数的控制器，柔性直流输电逆变侧输出功率1～3 s之间有功功率的标准差为9.673 3。逆变侧控制器采用单纯形优化后，逆变侧输出功率1～3 s之间有功功率的标准差为3.714。逆变侧控制器采用遗传算法优化后，逆变侧输出功率1～3 s之间有功功率的标准差为7.956 5。

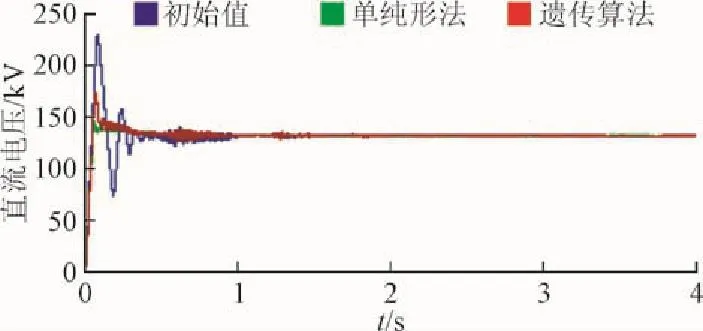
图13　直流电压Flg. 13 DC Voltage

由于柔性直流输电系统的直流电压是由逆变侧来来控制，而逆变侧系统连接的是无穷大电网，所以柔性直流输电直流侧电压不会随风电场的风速波动而波动。由于优化的目标函数中包含直流电压一项，所以直流电压的最大超调量由优化前的233.452降低至176.425（遗传算法）和151.63（单纯形法）。而优化后的系统中直流电压的震荡次数也明显减小。

由表2可以看出，无论在何种控制器参数下，逆变侧有功功率的波动都小于整流侧有功功率的波动，即柔性直流输电本身的特性即能够平抑风电场的输出波动，起到削峰填谷的效果，具有鲁棒性，适合风力发电并网。为了便于比较，本文中所做仿真采用同一个随机风速，优化后的参数能够使得风力发电机的输出波动减小，对于波动方差这一指标来说，单纯形法的优化结果要优于遗传算法。

表2　不同优化结果的输出方差Tab. 2 0utput varlance of dlfferent optlmlzatlon results

所做仿真中稳定额定风速情况下风电场有功功率额定值为75 MW。由表3可以看出，单纯形法优化后的结果均值偏离额定值较多，即单纯形优化后的控制系统使得风力发电机经柔性直流输电并入电网的能量相对减少，而遗传算法优化后的结果偏离额定值较小。由于积分时间常数是用来减小系统的稳态误差，这与表4中优化后的积分时间常数相一致。同时，表3中整流侧有功功率和逆变侧有功功率之间的差值是由换流站，输电线路以及变压器的损耗造成的。

表3　不同优化结果的输出均值Tab. 3 0utput mean values of dlfferent optlmlzatlon results

表4　不同优化结果的参数值Tab. 4 Parameters of dlfferent optlmlzatlon results

表4中，P1和I1是柔性直流输电风电场侧有功功率控制的PI控制器参数，P3和I3是柔性直流输电电网侧直流电压PI控制器的控制参数，P2，I2和P4，I4分别是整流和逆变侧的电流内环控制器参数。

为了测试该系统在故障情况下的动态响应，本文在系统仿真中的3 s时，在系统逆变侧交流电网引入三相接地短路故障，故障持续时间0.05 s。

如图14所示，在逆变侧发生故障后，整流侧有功功率输出迅速下跌，当柔性直流输电系统控制器采用初始值参数时，系统发生震荡，故障切除后最大超调量达到160 MW，系统失去稳定（恒定风速则不会失去稳定），而参数优化后，系统能够在故障切除后跟随风速变化，与图11稳态情况相一致。采用遗传算法优化后的控制器在发生故障后波动较为频繁，而采用单纯形法优化后的控制器能够恢复到稳定运行状态，与图11相一致。

图14　引入故障情况下整流侧有功功率Flg. 14 WF-VSC actlve power after fault ls lntroduced

如图15所示，系统受到故障扰动后，采用初始值参数的控制器使得系统在故障切除后失去稳定，发生震荡，最大超调量达到220 MW，采用单纯形优化后的控制器在故障切除后的0.01 s内恢复到稳定运行能够状态，且系统几乎无超调量，但在3.5 s后有功功率的波动又增加。采用遗传算法优化后的控制器需要在故障切除后的1s后恢复到稳定运行状态，遗传算法的有功功率的高频波动很少。

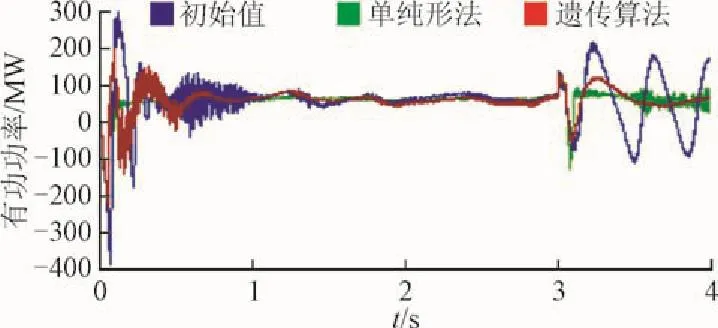
图15　引入故障情况下逆变侧有功功率Flg. 15 G-VSC actlve power after fault ls lntroduced

如图16所示，在原始参数情况下，故障切除后，直流电压发生振荡，最大超调量达到215 kV。采用单纯形改进的控制器超调量很小，能够在故障切除后的0.01 s内恢复到稳定状态。采用遗传算法优化后的控制器需要在故障切除后0.8 s后回到稳定运行状态，超调量为174.25 kV。

图16　引入故障情况下直流侧电压Flg. 16 DC Voltage after fault ls lntroduced

6　结论

本文建立了风电场的聚合模型以及柔性直流输电模型，风电场经柔性直流输电并入交流电网。采用单纯形和遗传算法两种启发式优化算法分别对该系统进行了参数优化，通过仿真结果可以得出如下结论：

1）在风电并网中，柔性直流输电逆变侧输出功率的波动要小于整流侧风电场输入功率的波动，仿真结果显示其波动方差减小了27.6%，柔性直流输电较好地平抑了风电场的功率波动。这说明柔性直流输电能够减小风电场的输出波动对电网的影响。

2）采用启发式优化算法优化后的控制器较好地减小了风电场输出功率波动对并网功率的影响，仿真结果显示采用单纯形法和遗传算法优化控制器参数后，并网有功功率方差比优化前减小了61.5% 和17.7%。使得风力发电并网功率变得更加平滑，风电场输出功率能够更好地适应电网所需要的并网准则。

3）2种优化算法各有优点：在启动阶段，遗传算法优化后的结果相比单纯形法优化的结果有更好的响应速度，控制器动态响应性能增强；启动完成后，单纯形法的优化结果对于平抑功率的波动好于遗传算法，控制器鲁棒性增强。

4）在故障响应情况下，故障切除后，优化后的控制器能够很快恢复稳定状态，而未优化参数的系统会容易失去稳定。单纯形法在故障切除后能够更快的恢复，且有较小的超调量。同时，直流电压的平衡决定着风电场并网的稳定与否。风速波动情况下，在遇到电网侧故障扰动时会使得风电场并入系统的功率发生振荡，通过优化参数能够改善这一情况。

综上所述，采用启发式优化算法能够改善风电场经柔性直流输电系统的动态响应能力。在风速大幅变化的情况中，优化后的柔性直流输电系统更能平抑风电场输出功率波动。2种遗传算法各有优劣，对于采用何种优化需要根据工程实际进行选择。

参考文献

[1]赵成勇.柔性直流输电建模和仿真技术[M].北京：中国电力出版社，2014.

[2]廖勇，王国栋.双馈风电场的柔性高压直流输电系统控制[J].中国电机工程学报，2012，32（28）：7-15. LIAO Yong，WANG Guodong. VSC-HVDC system contro1 for grid-connection of DIFG wind farms[J]. Proceedings of the CSEE. 2012，32（28）：7-15（in Chinese）.

[3]范心明，管霖，夏成军，等.风电场交直流混合输电并网中VSC-HVDC的控制[J].中国电机工程学报，2014，34（28）：4781-4790. FAN Xinming，GUAN Lin，XIA Chengjun，et a1. Contro1 of VSC-HVDC in AC/DC hybrid transmission with wind farms integrated[J]. Proceedings of the CSEE，2014，34 （28）：4781-4790（in Chinese）.

[4]郭春义，赵成勇，李广凯，等.基于SimP1ex算法的VSCHVDC控制参数优化[J].电力自动化设备，2010，30（9）：13-17. GUO Chunyi，ZHAO Chengyong，LI Guangkai，et a1. Contro1 Parameter oPtimization based on SimP1ex a1gorithm for VSC-HVDC[J]. E1ectric Power Au-tomation EquiPment，2010，30（9）：13-17（in Chinese）.

[5]陈蔓，陆继明，毛承雄，等.基于遗传算法的优化控制在VSC-HVDC中的应用[J].电力系统及其自动化学报，2006，18（4）：19-23. CHEN Man，LU Jiming，MAO Chengxiong，et a1. APP1ication of genetic a1gorithm based oPtima1 contro1 in VSC-HVDC[J]. Proceedings of the CSU-EPSA. 2006，18 （4）：19-23（in Chinese）.

[6]于永生，冯延晖，江红鑫，等.海上风电经VSC-MTDC并网研究[J].高压电器，2015，51（10）：26-33. YU Yongsheng，FENG Yanhui，JIANG Hongxin，et a1. Research on offshore wind farm integration via VSCMTDC[J]. High Vo1tage APParatus，2015，51（10）：26-33 （in Chinese）.

[7]陈树勇，徐林岩，孙栩，等.基于多端柔性直流输电的风电并网控制研究[J].中国电机工程学报，2014，34：32-38. CHEN Shuyong，XU Linyan，SUN Xu，et a1. The contro1 of wind Power integration based on mu1ti -termina1 high vo1tage DC transmission with vo1tage source converter[J]. Proceedings of the CSEE. 2014，34：32-38（in Chinese）.

[8]汤广福.基于电压源换流器的高压直流输电技术[M].北京：中国电力出版社，2010：132-144.

[9]张兴，张崇巍. PWM整流器及其控制[M].北京：机械工业出版社，2012：88-106.

[10]李环平，杨金明.基于PSCAD_EMTDC的大型并网风电场建模与仿真[J].电力系统保护与控制，2009，37（21）：62-66. LI HuanPing，YANG Jinming. Mode1 and simu1ation of 1arge grid connected wind farm based on PSCAD_EMTDC[J]. Power System Protection and Contro1，2009，37（21）：62-66.

[11] CONROY J，WATSON R. Aggregate mode11ing of wind farms containing fu11-converter wind turbine generators with Permanent magnet synchronous machines -transient stabi1ity studies[J]. IET Renewab1e Power Generation，2009，3（1）：39-52.

[12]夏玥，李征，蔡旭，等.基于直驱式永磁同步发电机组的风电场动态建模[J].电网技术，2014，38（6）：1439-1445. XIA Yue，LI Zheng，CAI Xu，et a1. Dynamic mode1ing of wind farm comPosed of direct—driven Permanent magnet synchronous generators[J]. Power System Techno1ogy，2014，38（6）：1439-1445（in Chinese）.

[13]杨勇波，江波，杨华云，等.风电场动态等值及其在暂态稳定分析中的应用[J].中国电力，2011，44（7）：66-70. YANG Yongbo，JIANG Bo，YANC Huayun，et a1. Dynamic equiva1ence of wind farms and its aPP1ication to Power systemtransient stabi1ity ana1ysis[J]. E1ectric Power，2011，44（7）：66-70（in Chinese）.

[14]肖宏峰.基于单纯形多向搜索的大规模进化优化算法[D].长沙：中南大学，2009.

[15]项国波. ITAE最佳控制[M].北京：机械工业出版社，1986.

[16]张勇军.电力系统无功优化的灾变遗传算法及MAS模型研究[D].广州：华南理工大学，2004：17-30.

[17]于永生，冯延晖，江红鑫，等.一种风电场经柔性直流输电并网控制方法改进探讨[J].电网与清洁能源，2015，31（7）：81-87. YU Yongsheng，FENG Yanhui，JIANG Hongxin，et a1. An imProvement on 1arge-sca1e wind Power grid integration through VSC-HVDC[J]. Power System and C1ean Energy，2015，31（7）：81-87（in Chinese）.

[18] ZHAO Xiaodong，LI Kang. Contro1 of VSC-HVDC for wind farm integration based on adaPtive backstePPing method[C]. IEEE Internationa1 WorkshoP on Inte11igent Energy System（IWIES），2013：64-69.

[19] WANG Liying，ERTUGRUL N. Se1ection of PI comPensator Parameters for VSC-HVDC system using decouP1ed contro1 strategy[C]. 20th Austra1asian Universities Power Engineering Conference（AUPEC），2010：1-7.

[20] YANG Jin，O＇REILLY J，FLETCHER J E. An overview of DC cab1e mode1ing for fau1t ana1ysis of VSC -HVDC transmission systems[C]. 20th Austra1asian Universities Power Engineering Conference（AUPEC），2010：1-7.

[21]陕华平，肖登明，薛爱东.大型风电场的风资源评估[J].华东电力，2006，34（2）：16-17. SHAN HuaPing，XIAO Dengming，XUE Aidong. Wind resource assessment for 1arge wind Power fie1ds[J]. East China E1ectric Power，2006，34（2）：16-17（in Chinese）.

于永生（1989—），男，硕士研究生，主要从事柔性直流输电，风电并网等方面的研究工作；

冯延晖（1977—），男，博士，副教授，主要研究方向为可再生能源发电，电力电子与电力传动，新能源并网控制。

（编辑徐花荣）

Project SuPPorted by Jiangsu ToP Six Ta1ent Summit Fund（ZBZZ-045）；Natura1 Science Fund of Jiangsu Province（BK 20131350）；the Fundamenta1 Research Funds for the Centra1 Universities（309150 11324）；Returned Overseas Students Preferred Funding.

0ptlmlzatlon of Wlnd Farm Grld Integratlon vla VSC-HVDC Conslderlng Randomness of Wlnd Energy

YU Yongsheng，FENG Yanhui，JIANG Hongxin，QIU Yingning
（Schoo1 of Energy and Power Engineering，Nanjing University of Science and Techno1ogy，Nanjing 210094，Jiangsu，China）

ABSTRACT：As energy crisis has draws more and more attention a11 around the wor1d，wind energy is getting more and more imPortant as a kind of renewab1e and c1ean energy. The outPut of the wind energy，however，is subjected to changes of wind sPeed，thus，the wind farm outPut often f1uctuates. This PaPer bui1ds the aggregate wind farm mode1 and the VSC -HVDC mode1. In order to stabi1ize the f1uctuation of the wind farm outPut，the PaPer adoPts the SimP1ex Method and Genetic A1gorithm resPective1y to oPtimize the contro11er of VSC-HVDC. The resu1t shows that both of these two different ways he1P to constrain the f1uctuation of the outPut of the wind farm and have strong engineering aPP1ication va1ue.

作者简介：

收稿日期：2015-06-17。

基金项目：江苏省六大人才高峰项目（ZBZZ-045）；江苏省自然科学基金面上项目（BK20131350）；中央高校基本科研业务费专项资金资助（30915011324）；留学回国人员择优资助项目。

文章编号：1674-3814（2016）01-0075-10

中图分类号：TM743

文献标志码：A