电网不确定运行环境下的发电计划鲁棒优化研究

李利利，丁恰，涂孟夫，戴则梅（国电南瑞科技股份有限公司，江苏南京　211106）



电网不确定运行环境下的发电计划鲁棒优化研究

李利利，丁恰，涂孟夫，戴则梅
（国电南瑞科技股份有限公司，江苏南京211106）

KEY W0RDS：generation schedu1ing；uncertainty of Power grid；robust oPtimization；security constrained unit commitment （SCUC）；economica1 disPatch

摘要：以风电和光伏发电为代表的大规模间歇式能源接入，显著增加了电网运行的不确定因素。鲁棒优化方法由于其具有的独特优势，目前已经被初步用于研究发电计划问题。介绍了鲁棒优化算法理论，建立了发电计划鲁棒优化的数学模型，提出了基于原始分解的求解算法。以IEEE RTS标准算例系统进行分析计算，验证了该算法的有效性。

关键词：发电计划；电网不确定性；鲁棒优化；安全约束机组组合；经济调度

发电计划是电网调度运行的重要环节，其关键内容为机组启停优化与出力分配[1]。基于电源的可靠性以及负荷的可预测性，传统发电计划决策是一个确定性的优化问题，以安全约束机组组合（security constrained unit commitment，SCUC）和安全约束经济调度（SCED）为核心的调度计划软件已在国内外大规模电力系统中得到成功应用[2-4]。

近年来，以风电为代表的新能源发电作为解决能源危机和环境问题的重要手段得到了快速发展。在新能源优先接纳的背景下，电网调度有责任通过最大程度的利用新能源来实现系统平衡。然而，新能源发电受自然因素的影响，具有波动性、低可控性和不完全可预测性等特点，大规模新能源发电并网带来了明显的不确定性因素，增加了电力系统调度的难度。不确定参数的引入给确定性发电计划决策带来了新的挑战。

目前，缺乏有效的技术手段应对电网运行不确定性带来的挑战，为了保证电网的安全稳定运行，即电力调度部门采用的是相对保守的发电计划，即电网必须预留足够的系统备用容量以应对新能源的不确定性[5]，从而降低了常规机组发电效率，这也影响了对新能源的有效接纳。

因此，面对电网运行中的大量不确定性，学者开始关注能否在发电计划编制过程中考虑各种不确定性因素，通过合理调用各种可用资源，制定出可行且优化的发电计划，充分消纳新能源发电，实现电网安全与经济运行的最佳协调[6]。

随机规划是发电计划优化中建模不确定性的传统方法[7-9]，其建立的是一种期望值模型，通过预先抽样典型离散场景进行优化决策。随机规划的不足之处在于需要不确定性因素的精确概率分布，而在实际应用中往往难以获得。同时，其优化结果只保证离散场景下的可行性，应用于电网调度时存在安全风险。

鲁棒优化能够基于适度的不确定性数据的分布信息来建模不确定因素，其计算结果对不确定集合内的任意元素都保证约束可行性[10]，应用鲁棒优化求解发电计划优化问题逐渐得到国内外学者的关注[11-13]。

本文建立和分析了发电计划鲁棒优化的模型和算法，采用电力系统的标准测试算例进行仿真测试，对优化结果从适应性与经济性2个方面进行分析，验证了鲁棒优化方法的有效性。

1　鲁棒优化理论

在传统数学优化模型中，通常假设模型中的参数是确切已知的，从而忽略了数据不确定性对模型可行性和最优性的影响，这种忽略可能会造成优化解无法满足关键约束情况的产生。因此，需要找到一种优化方法使得优化解能够满足不确定数据的所有实现，即鲁棒优化。

鲁棒优化是一种求解参数不确定优化问题的建模方法，其特点是：

1）鲁棒优化的约束强调的是硬约束，要求优化问题的解对于任何一个不确定参数的实现都必须可行，满足此要求的解称为鲁棒可行解。

2）鲁棒优化的目标是以最坏情况下的优化为基础来考虑不确定因素对优化目标的影响。目标函数采用极小化极大值结构（min-max），通过优化鲁棒可行解中的目标最坏解，进而获得最优结果，使得目标值对参数扰动不敏感。当参数在给定的集合内变化时，优化结果仍然是可行的，且目标值不会高于优化目标。

3）鲁棒优化不需要概率分布假设，只需要给出不确定参数的集合，集合内的所有值对于鲁棒优化而言是同等重要的，如图1所示。

对于电力系统而言，发电计划的实际不可行，会造成极大的运行风险，包括安全风险与经济代价。鲁棒优化在不确定信息的需求度以及优化结果的适应性方面，相比传统方法具有明显的优势。

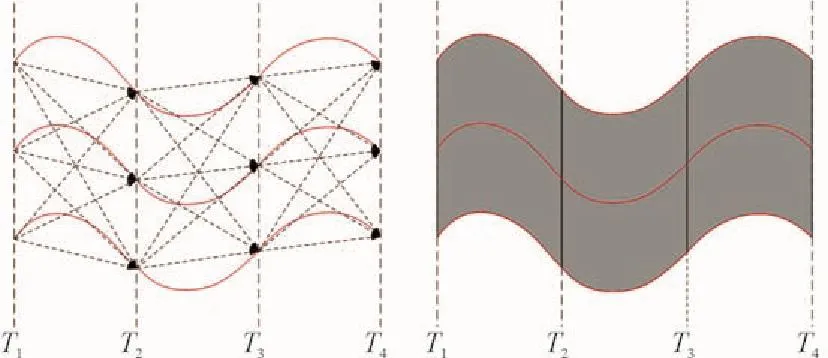
图1　鲁棒优化建模不确定性示意图Flg. 1 Schematlc of the uncertalny of the robust optlmlzatlon modellng

2　发电计划鲁棒优化模型

2.1不确定性集合

应用鲁棒优化需要对问题的不确定性因素进行有效描述。与随机规划采用概率分布描述不同，鲁棒优化把不确定性所有可能的实现预先限定在一个确定的集合中。对于该集合中的每个元素，鲁棒优化的最优解都能够保持可行性。

具体到电力系统发电计划领域，不确定参数主要来源于预测信息的不准确，如负荷信息、间歇式能源发电等。由于预测信息的误差往往具有连续性，通常采用区间形式的“盒式”不确定集合来描述不确定参数的波动范围。以负荷为例，系统负荷可以在区间[Lu，Ld]范围内波动，Lu、Ld分别为区间的上界和下界，其数值通常由历史数据或负荷区间预测获得。

2.2发电计划2阶段特性

电力不能大量存储的特点要求系统发电与用电保持实时平衡，这就需要调度中心根据对电网实际运行状态的预测，提前安排充足的发电资源，以满足实时阶段的供电可靠性要求。火电机组的启停响应较慢，需要一个时间过程，而开机之后机组的有功调节响应较快。发电计划从时序上划分为机组组合与经济调度2部分。

考虑电网预测信息的不确定性后，不确定因素在事前是不完全可知的，直到实际出现的时刻才是已知的。而此时，为保证供电的可靠性，需要调用系统在线的可用发电资源，实现电力的实时平衡。因此，机组启停决策变量应该在不确定因素实现之前，获得具体的求解结果。经济调度决策变量要求满足于负荷平衡的等式约束，从而依赖于不确定因素的实际值，需要在不确定因素实现之后，才能获得其具体的求解结果。因此，发电计划鲁棒优化也是一个2阶段的优化问题。

2.3鲁棒优化模型

基于鲁棒优化理论与发电计划2阶段决策特性，模型的优化目标为最小化给定不确定集合中最坏情况下的发电总成本。采用极小化极大值结构的目标函数，可最大程度地降低不确定因素对发电成本的影响，而不确定集合则控制着优化决策的保护水平。

在确定性发电计划模型的基础上，以负荷的不确定性为例建立鲁棒优化模型，其他连续的不确定性因素（如风电、光伏发电等）建模与之类似：

约束条件为：

式中：I为系统中参与调度的机组数；T为系统调度周期所含时段数；Si，t为机组i时段t的开机成本；Ci为机组i的成本曲线；ui，t、yi，t、zi，t分别为机组i在t时刻的启停状态、开机标志与停机标志；pi，t为机组i在t时刻的出力；UTi和DTi分别为机组i的最小开机时间和最小停机时间；lt为系统t时刻的总负荷；L为负荷的不确定集合；pi，max、pi，min分别为机组i输出功率的上下限；Δi为机组i爬坡速率的最大值；LiJ为支路i J的潮流上限；M为电网计算节点集合；li，t为节点负荷功率；Si，J，t为节点i的注入功率对支路i J的灵敏度。式（2）、式（3）为机组启停状态约束；式（4）、式（5）为机组最小开停机时间约束；式（6）系统平衡约束；式（7）为机组出力上下限约束；式（8）为机组爬坡速率约束；式（9）为电网安全约束。

需要指出的是，模型中系统负荷lt并不是确定值，而是由不确定集合L描述的随机参数。根据模型，在第一阶段的机组组合优化中，考虑了不确定集合L描述的所有可能的负荷情况，机组启停决策（ui，t、yi，t、zi，t）均保持可行性，因此结果是鲁棒的；在第二阶段的经济调度优化中，有功出力pi，t随着不确定性负荷值lt的变化而变化，目标为最小化不确定集合中最坏情况下的调度成本，从而降低考虑不确定因素后的发电总成本。

3　求解算法

第2节优化模型中，式（6）不再是常规的确定性的约束条件，而是依赖于不确定集合L的约束集，使得问题难以直接求解。普遍的做法是采用分解算法，通过分离模型中的机组组合（UC）与经济调度（ED）过程，将模型转化为显式的2阶段优化问题，从而迭代求解。鲁棒发电计划模型可以划分为的主问题与子问题。

主问题为机组组合模型，优化目标为：

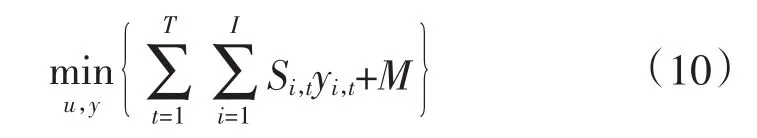
约束条件包括式（2）—式（5），并新增式（11）描述割平面约束。

子问题为经济调度模型，优化目标为：

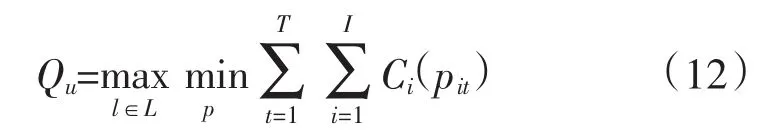
约束条件包括式（6）—式（9）。

模型中，全部离散变量以及只与其相关的约束条件归并到主问题中，连续变量及其相关的约束条件归并到子问题中。其中，M为主问题中的最坏情况下的调度成本变量；Qu为子问题的目标函数，且根据其结果信息生成主问题的割平面约束。

分解后，主问题转变为确定的混合整数规划问题，可以直接求解；而子问题的约束条件中仍包含不确定变量，无法直接求解。对于子问题，将其优化模型进行对偶转化，可以消去目标函数的max-min结构，并将约束条件中的不确定变量转化到目标函数中，消去了依赖于不确定集合L的约束集，使得问题转化为可以直接求解的优化问题。

基于分解算法原理，主问题在子问题产生的割平面的基础上，求解最优的开停机结果，并将其结果设为问题的下界；而子问题则在主问题产生的启停结果的基础上，求解最坏情况下的调度成本，将其结果设为问题的上界，并根据子问题结果中的最坏情况产生割平面返回至主问题。通过主问题与子问题之间的迭代，直至问题的上界与下界满足收敛条件，优化结束。

值得注意的是，不同于文献[11-12]采用的传统对偶分解方法，本文采用了与文献[14]相似的原始分解（Prima1 decomPosition）方法，该方法能够在每一次迭代过程中产生更多的割平面约束，从而可以获得更好的计算性能。

4　算例分析

采用IEEE RTS标准算例系统[15]测试发电计划鲁棒优化的计算效果。优化周期为1日24 h，共分为24个优化时段。设定系统负荷为不确定性因素，负荷在预测值的上下10%的波动区间内变化，以测试鲁棒优化模型对不确定因素的适应能力。

为评估鲁棒优化方法的计算效果，将其结果与备用调整方法进行对比。备用调整方法为基于负荷预测进行的确定性发电计划优化，其备用需求设定为与负荷的波动量一致。

评估过程为：

1）分别求解鲁棒优化模型与备用调整模型，获得相应的机组开停机结果。

2）在负荷波动区间范围内，随机模拟1 000个负荷场景。

3）基于上述确定的2种开停机结果，分别重复计算模拟场景下的经济调度问题。

4.1机组组合适应性分析

基于鲁棒优化获得的机组组合结果，计算1 000个场景下的经济调度问题，经济调度全部收敛。而基于备用调整获得的机组组合结果，同样计算1 000个场景下的经济调度问题，在多个场景下经济调度问题无法收敛，如表1所示。

表1　多场景下的经济调度收敛结果Tab. 1 Convergence result of the economlcal dlspatch wlth multlple load scenarlos

其中，基于备用调整方法获得的开停机结果计算经济调度问题，其中的不收敛场景如图2所示。

图2　备用调整方法的不可行场景Flg. 2 Infeaslble scenarlo of the reserve adjustment method

从图2可以看出，在该场景的第7时段与第8时段，负荷分别位于波动区间的下限与上限，经济调度问题受爬坡速率约束的限制而不收敛，亦即此机组组合结果不合理。虽然备用调整方法考虑了负荷波动的调峰因素，但没有精细考虑不同时段之间备用的可支持性，其获得的开停机结果难以适应所有区间内的负荷变化。而鲁棒优化方法要求优化问题的解对于任何一个不确定参数的实现都必须是可行的，机组组合结果能够适应负荷在区间内的任意变化，可有效提升系统运行的可靠性。

4.2经济性分析

为保证发电成本分析中经济调度问题的收敛性，松弛系统平衡约束，并设定松弛变量的惩罚因子为1 000 $/MW·h（算例中的机组平均发电成本为10 $/MW·h）。此设置的含义为，在目前确定的开停机基础上，实时调度阶段遇到发电能力不足的现象，因进行限电等操作而付出的代价。

在负荷预测的单场景下，基于机组组合结果计算经济调度问题，成本对比如表2所示。

表2　预测负荷下的经济调度成本对比Tab. 2 Cost comparlson of the economlcal dlspatch under the forecast load　$

由表2可知，在预测负荷条件下，基于鲁棒优化的经济调度总成本要高于备用调整方法，其中主要是组合成本相对较高。这是因为鲁棒优化不仅考虑了预测负荷的场景，还精细化地考虑了波动区间内的各种误差场景，从而造成预测负荷条件下的总成本相对较高，此即考虑不确定性的代价。

基于机组组合结果，分别计算1 000个模拟场景下的经济调度问题，平均成本对比如表3所示。

表3　多场景下的经济调度平均成本对比Tab. 3 Average cost comparlson of the economlcal dlspatch wlth multlple load scenarlos　$

由表3可知，当考虑多个场景时，虽然鲁棒优化的组合成本要高于备用调整，但是其惩罚成本为0，从而使得基于鲁棒优化的经济调度总成本要低于备用调整方法。鲁棒优化考虑了不确定集合内的所有场景，进而调用了更多的发电资源；而备用调整方法通过设置系统备用水平来考虑不确定性，并没有识别不确定因素的各种极端场景。

同时，基于备用调整结果的经济调度计算会产生惩罚成本，表明经济调度优化时存在约束松弛现象，这意味着备用调整只考虑预测负荷与备用约束，当考虑多个场景时，该确定性优化方法获得的机组组合结果不可行，而鲁棒优化获得机组组合结果则始终可行，具有更好的适应性。

5　结语

将鲁棒优化理论应用于考虑不确定性的发电计划优化问题，发电计划结果能够适应不确定集合内的所有可能运行场景，从而提高发电计划的鲁棒性。本文分析了发电计划鲁棒优化的数学模型和算法，并基于IEEE RTS标准系统构建算例，对发电计划的鲁棒优化方法与备用调整方法进行比较。结果表明鲁棒优化方法可以显著提升发电计划结果对不确定因素的适应性，并降低系统的平均发电成本，从而提高了电力系统实时运行的可靠性。

参考文献

[1]张智刚，夏清.智能电网调度发电计划体系架构及关键技术[J].电网技术，2009，33（20）：1-8. ZHANG Zhigang，XIA Qing. Architecture and key techno1ogies for generation schedu1ing of smart grid[J].Power System Techno1ogy，2009，33（20）：1-8（in Chinese）.

[2] STREIFFERT D，PHILBRICK R，OTT A. A mixed integer Programming so1ution for market c1earing and re1iabi1ity ana1ysis[C]// Proceeding of IEEE PES 2005 Genera1 Meeting，June 12-16，2005，San Francisco，USA：2724-2731.

[3]耿建，徐帆，姚建国，等.求解安全约束机组组合问题混合整数规划算法性能分析[J].电力系统自动化，2009，33（21）：24-27. GENG Jian，XU Fan，YAO Jianguo，et a1. Performance ana1ysis of mixed-integer Programming based a1gorithm for security constrained unit commitment[J]. Automation of E1ectric Power Systems，2009，33（21）：24-27（in Chinese）.

[4]陈之栩，李丹，张晶，等.华北电网安全节能发电优化调度系统功能设计[J].电力系统自动化，2008，32（24）：43-47. CHEN Zhixu，LI Dan，ZHANG Jing，et a1. Function design for north China grid security constrained convention dis-Patch oPtimization system[J]. Automation of E1ectric Power Systems，2008，32（24）：43-47（in Chinese）.

[5]王丹平，陈之栩，涂孟夫，等.考虑大规模风电接入的备用容量计算[J].电力系统自动化，2012，36（21）：24-28. WANG DanPing，Chen Zhixu，TU Mengfu，et a1. Reserve caPacity ca1cu1ation considering 1arge-sca1e wind Power integration[J]. Automation of E1ectric Power Systems，2012，36（21）：24-28.

[6] RUIZ P A，PHILBRICK C R，ZAK E，et a1. Uncertainty management in the unit commitment Prob1em[J]. IEEE Trans on Power Systems，2009，24（2）：642-651.

[7] WANG J H，SHAHIDEHPOUR M，LI Z Y. Security constrained unit commitment with vo1ati1e wind Power generation[J]. IEEE Transactions on Power Systems，2008，23（3）：1319-1327.

[8]叶荣，陈皓勇，王钢，等.多风电场并网时安全约束机组组合的混合整数规划解法[J]. 2010，34（5）：29-33. YE Rong，CHEN Haoyong，WANG Gang，et a1. A mixed integer Programming method for security constrained unit commitment with mu1tiP1e wind farms[J]. Automation of E1ectric Power Systems，2010，34（5）：29-33（in Chinese）.

[9]王林，杨佳俊，陈红，等.含风电场的电网潮流计算[J].电力电容器与无功补偿，2015，36（1）：49-53. WANG Lin，YANG Jiajun，CHEN Hong，et a1. Power f1ow ca1cu1ation of wind Power integrated systems[J]. Power CaPacitor & Reactive Power ComPensation，2015，36（1）：49-53.

[10] BEN-TAL A，NEMIROVSKI A. Robust oPtimization：methodo1ogy and aPP1ications[J]. Math. Program. Ser B，2002，92：452-480.

[11] JIANG R，WANG J，GUAN Y. Robust unit commitment with wind Power and PumPed storage hydro[J]. IEEE

Transactions on Power Systems，2012，27（2）：800-810.

[12]魏韡，刘锋，梅生伟.电力系统鲁棒经济调度：（一）理论基础[J].电力系统自动化，2013，37（17）：37-43. WEI Wei，LIU Feng，MEI Shengwei. Robust and economica1 schedu1ing methodo1ogy for Power systems Part one theoretica1 foundation[J]. Automation of E1ectric Power Systems，2013，37（17）：37-43（in Chinese）.

[13]魏韡，刘锋，梅生伟.电力系统鲁棒经济调度：（二）应用实例[J].电力系统自动化，2013，37（18）：60-67. WEI Wei，LIU Feng，MEI Shengwei. Robust and economica1 schedu1ing methodo1ogy for Power systems Part two aPP1ication examP1es[J]. Automation of E1ectric Power Systems，2013，37（18）：60-67（in Chinese）.

[14] SHAHIDEHPOUR M，FU Y. APP1ying benders decom-Position to Power systems[J]. IEEE Power Energy Magazine， 2005，33（2）：20-21.

[15] Re1iabi1ity Test System Task Force. The IEEE re1iabi1ity test system-1996[J]. IEEE Transactions on Power Systems，2012，27（2）：800-810.

李利利（1987—），男，硕士，工程师，主要研究方向为电力系统运行和优化；

丁恰（1974—），男，硕士，研究员级高级工程师，主要研究方向为电力系统运行与控制；

涂孟夫（1976—），男，硕士，高级工程师，主要研究方向为电力系统经济运行；

戴则梅（1973—），女，硕士，研究员级高级工程师，主要研究方向为电力系统自动化。

（编辑董小兵）

Project SuPPorted by Nationa1 High Techno1ogy Research and Deve1oPment Program of China（863 Program）（2012AA050207）；State Grid CorPoration of China.

Research on Robust 0ptlmlzatlon of Generatlon Schedullng under Uncertaln 0peratlng Condltlons of Power Grld

LI Li1i，DING Qia，TU Mengfu，DAI Zemei
（NARI Techno1ogy Co.，Ltd.，Nanjing 211106，Jiangsu，China）

ABSTRACT：Integration of 1arge-sca1e intermittent energy such as wind Power and Photovo1taic Power increases the uncertainty of the Power grid oPeration significant1y，bringing new cha11enges to the traditiona1 mode1s of the Power generation schedu1ing. Due to its unique advantages，the robust oPtimization has been used to study the Power generation schedu1ing initia11y. In this PaPer，the theory of robust oPtimization a1gorithm is introduced and the mathematica1 mode1 of the robust oPtimization is estab1ished and the so1ution a1gorithm based on the origina1 decomPosition is ProPosed. Fina11y，the effectiveness of the ProPosed a1gorithm is verified by the ana1ysis and ca1cu1ation of the examP1e system by the IEEE RTS standard.

作者简介：

收稿日期：2015-05-25。

基金项目：国家高技术研究发展计划（863计划）资助项目（2012AA050207）；国家电网公司科技项目“大规模新能源接入下基于概率分析的调度计划及安全校核关键技术研究”。

文章编号：1674-3814（2016）01-0014-05

中图分类号：TM734

文献标志码：A