基于JADE的室内多组分混合污染气体定量分析
王 骁,李 博,冯小琴
基于JADE的室内多组分混合污染气体定量分析
王 骁1,李 博1,冯小琴2
(1. 中北大学仪器科学与动态测试教育部重点实验室,山西 太原 030051;2. 北方自动控制技术研究所,山西 太原 030006)
检测室内有害气体得到的红外光谱为混合有害气体的红外光谱,针对吸收谱带相互交叠的混合气体定性定量不容易的问题,提出基于特征矩阵联合近似对角化(joint approximative diagonalization of eigenmatrix,JADE)的特征提取方法,该方法通过分析数据的高阶统计量信息,充分挖掘原始数据隐含的信息,以便准确地区分出混合气体中各物质的光谱,同时应用基于正则理论的支持向量机(SVM)对提取出来的独立信号源建立多维数据定量分析的模型。实验结果表明,混合气体中各组分的定量分析相关系数均保持在0.9991以上,验证了该特征提取方法的准确性。
特征矩阵联合近似对角化;定量分析;多组分;支持向量机
0 引言
随着社会进步,人类日常生活水平提高,人们对于居住房屋的环境和氛围要求逐渐增高,名类繁多的装修风格则为各类人群提供了满足需求的可能。我国房屋装修以及家居用品中使用的新型复合材料和化学合成材料质量参差不齐,大部分含有多类有毒有害的物质,长时间接触这些有害物质严重影响了人们的身心健康[1-3]。室内空气检测旨在分析室内空气质量现状给人们提供一个数据考量,这在降低室内空气污染中有着重要的意义[4-5]。
利用红外光谱表[6-7]征物质物理属性的良好能力对室内多种污染气体进行分析检测,对于各组分污染气体的定量分析则建立在良好的特征提取基础之上,合理充分地挖掘测试数据的信息是一项繁杂重要的工作。而基于高阶统计量信息的JADE有良好的盲源分离性能被用于矢量水听器阵列信号辨识[8],雷达信号抗主瓣干扰[9],假药快速检测分析[10]。对于实际红外测量应用中,目标光谱特征上存在各种未知干扰成分、基线漂移和噪声信号,吸收谱线上有较多的重叠,而我们感兴趣的光谱信号仅有一小部分,针对红外光谱数据的非线性、小样本以及空间光谱维数大等问题,适当利用高阶统计量挖掘信息全貌则为光谱的特征提取提供了一种新的尝试。
支持向量机(support vector machine,SVM)是建立在统计学习理论的VC维理论和结构风险最小原理基础上的机器统计学习方法[11],对于小样本、非线性高维模式识别有很大优势,两者结合使用对污染气体的高维度、非线性红外光谱特征进行快速提取与识别,并定量解析,有效地发挥了2种方法的统计优势,扬长避短的结合提高了各气体定性定量分析的准确度。
1 算法实现
1.1 特征矩阵联合近似对角化
特征矩阵联合近似对角化(joint approximative diagonalization of eigenmatrix,JADE)是由法国学者Cardoso提出的一种处理多导信号的方法,是独立分量分析的一种批处理算法[12-13]。JADE是对引入的多变量数据的四维计量矩阵对其特征分解的简化算法,它通过求原始数据球化后的全部四阶累积量构造一组加权重的阶累积量矩阵,然后寻求一个酉变换矩阵对这组四阶累积量矩阵进行联合对角化逼近从而估计出混合矩阵和信源。本文采用这种方法对混合气体红外光谱进行特征提取。
设一个待观测的维信号=[1,2, …,x]T由个源信号=[1,2, …,s]T线性混合而成:
=+(1)
式中:是线性混合矩阵;为噪声信号矩阵。通过JADE可计算出混合矩阵,解混矩阵和源信号。对于红外光谱信号来说,×(≤)可看做个测试点在处波长的红外光谱信号矩阵,用×(≤)表示单一物质的光谱矩阵,每一行均可看成是一种物质的光谱信息,×则是混合矩阵,能体现出混合光谱中的相对浓度。使用JADE完成各成分分离时,令=[1,2, …,z]T为原始数据=[1,2, …,x]T球化后的观察矢量,为任意×矩阵,的四阶累积量矩阵()的第,元素定义如下:
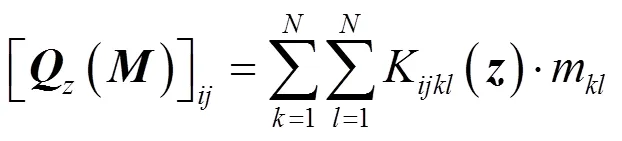
式中:K()是中的第,,,四个分量的四维累积量,()是×的对称阵,m是矩阵的第,个元素。()中,点上的元素反映了给定,下全部cum(x,x,x,x)的加权和,其权重是对应于,点的元素值。由此矩阵()概括了多通道数据的全部四维累积量。酉阵表示为混合矩阵和球化阵的乘积=,且=。令v,=1~代表中各列=[1, …,, …,],且=[1, …,]T,则阵可取为:

其第,个元素为m=vv。四阶累积量矩阵()可分解为:
()=(4)
其第,元素表示为[()]=m,式中=4()是信源的峰度,()的特征矩阵为,其特征值为=4()。由于[()]=4(),它的一个特征分解为=T,则()一定可表示为:


通过式(6)寻求能通过T()将()对角化的酉阵,对混合矩阵做出辨识和分解:
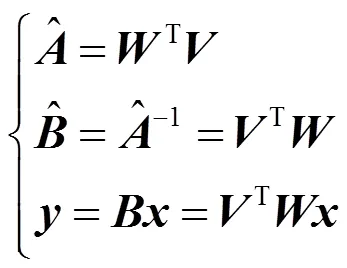
式中:为分离出的信源。
1.2 支持向量机
对多组分气体进行定量分析实质上是考虑实值函数的估计问题,目标是估计一个几乎没有先验知识的函数()[14],其满足:
=()+(8)
式中:为预估的偏差;是一个维输入向量;是室内混合污染气体的标定浓度。估计是基于个样本来实现的,Z~(x,y),=1, 2, …,是服从独立同分布(,)=()(|)的概率。因此预估式(8)可以表示为:

学习过程中,选择最优函数(,0)来最小化预测的期望风险,∈是预测函数集合的广义参量。通过方差损失函数进行回归估计,以表征预测结果的好坏:

但学习方法所支持的函数集合(,)不一定包含式(9)所对应的回归函数,因此学习的问题是仅使用训练样本数据寻找预测函数(,0)实现最小化期望风险[15]:
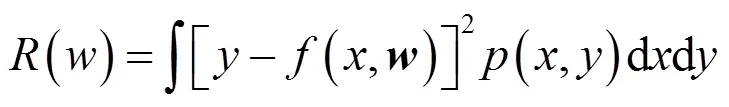
函数泛化能力通常用风险大小来表示,实际中我们往往认为未知的函数()或是样本分布()都是非时变的,所以利用先前的数据所做的估计才是有意义的,按照经验风险最小实现实际模型的参量估计:

建模的目标是最小化经验风险,虽说理论上许多分类函数在样本集上的准确率很高,但是实际分类的结果却不尽人意。因此即使确定了预测函数最小的经验风险,也还是无法保证期望风险为最小。因此统计学习的就是为了寻求结构风险的最小化:
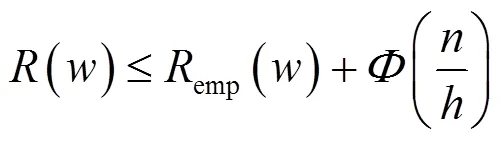
式中:(/)是学习的置信区域;是预测函数的VC维数(Vapnik-Chervonenkis dimension)。SVM正是这样一种努力最小化结构风险的算法。样本数量与分类函数的VC维决定了置信风险的结果,大量的给定样本数量和越小的VC维数会保证越小的置信风险。在根据式(12)中在有关学习复杂控制的结构风险最小化框架下,可以依靠样本灵活的适应性把预测函数集(,)排列成一序列子集的嵌套。式S={(,),∈}中元素的VC维都具有有限性,为了确保在同一个预测函数都的置信范围相同,必须利用式(13)使函数子集能够分别按照VC维的大小进行排列,同时遵循结构逢小最小化原则,为最优模型提供最小真实风险的上界函数。为了确保在这个空间中可构造最优分类超平面作为决策曲面,最大化正例和反例之间的隔离边缘。因此输入向量可通过已确定的非线性映射映射到高维特征空间中内,所以在权空间中的优化可以表达为:


式中:是调和常量,():R® R是核空间的映射函数,是均方误差和正则量化之和的损失函数,映射函数与核函数可根据Mercer条件表示为:

因此最优化的预测函数为:

2 结果与讨论
2.1 JADE光谱分离
使用北京瑞利分析仪器公司生产的WQF-520型傅里叶变换红外光谱仪搭建实验系统,配套其提供的100mm常规密闭气室。采用七星华创电子股份有限公司生产的质量流量计精密的控制气体浓度,为了保证实验的准确性,需要对仪器用高纯的N2进行冲洗,然后通入混合气体,不同浓度的氨气(NH3)、甲醛(CH2O)、氮气(N2)通过流量计进入密闭气室,经过重复多次实验采集到100条混合气体样品的光谱如图1所示,其中光谱分辨率为4cm-1,波数范围大气窗口700~1300cm-1。

图1 采集到的100条样品透过率光谱
采集到的混合气体的光谱数据经过JADE算法的处理,将吸收峰交错重叠的两种纯物质气体分离出来,并反演出两种纯物质的光谱。
图2为JADE分离出的独立成分分量,其中上面的独立成分为甲醛(CH2O)的透过率特征谱图,下面的独立成分为氨气(NH3)的透过率特征谱图。

图2 JADE分离出的独立成分
图3是恢复重建的浓度分别为1000mol/L的氨气(NH3)和95mol/L甲醛(CH2O)的透过率光谱。

图3 恢复某浓度下的NH3和CH2O透过率光谱
2.2 SVM定量分析
根据上述分离实验得到的100条氨气和甲醛光谱透过率数据,各自从中随机挑选出80组数据作为训练样本,剩下的20组数据作为建立浓度预测模型的测试样本,利用SVM建立浓度预测模型,定量分析得到的测试集输出浓度和相对误差结果,如图4和图5所示。
由图4、图5的结果可计算得到NH3与CH2O相关系数分别为=0.9992和=0.9991,二者均方根误差分别为MSE=27.9312和MSE=0.7931,相关系数和均方根误差说明定量分析结果比较精确,从而说明JADE方法在多组分混合气体定性分析中具有很高的分离性能,能够精确的将吸收峰混叠的2种气体区分开来。
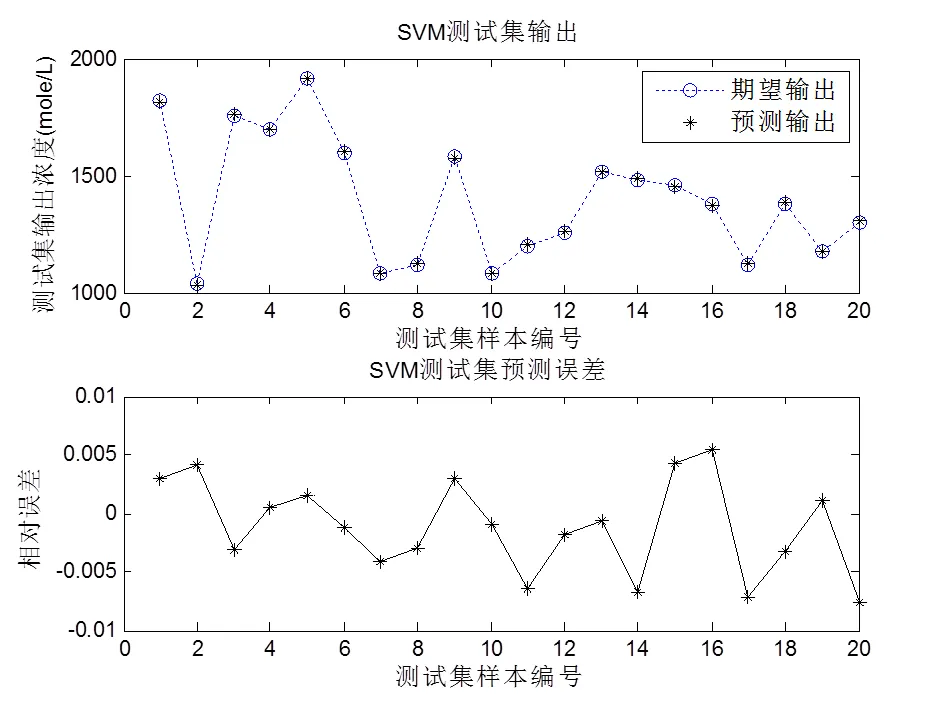
图4 NH3测试集预测结果
3 结论
将特征矩阵联合近似对角化算法应用到室内污染气体检测中,提高了定性分析的稳定性,结合支持向量机良好的泛化学习能力和推广能力构建出混合污染气体的定性定量分析模型,两种算法的有机结合取长补短,基本能够达到混合气体的定性定量要求,而且这样的结合也为精确测量多组分混合气体提供了参考。
[1] 刘紫红, 洪琦. 室内装修污染源分析及防治措施[J]. 绿色科技, 2015(5): 197-199.
LIU Zihong, HONG Qi. Analysis and prevention of indoor decoration pollution source[J]., 2015(5): 197-199.
[2] 郑家鑫. 住宅装修甲醛的释放因素探究[J]. 产业与科技论坛, 2015, 15: 79-80.
ZHENG Jiaxin. Research on releasing factor of formaldehyde in residential decoration[J]., 2015, 15: 79-80.
[3] 陈猛. 试论室内空气污染危害与解决措施[J]. 黑龙江科技信息, 2014(4): 2-2.
CHEN Meng. Study on harm and solution of indoor air pollution[J]., 2014(4): 2-2.
[4] 陈希尧. 浅谈室内装修带来的环境污染及预防措施[J]. 资源节约与环保, 2014(11): 88-88.
CHEN Xiyao. Pollution and prevention of indoor decoration[J]., 2014(11): 88-88.
[5] 王登山. 室内空气污染危害及其净化技术的探究[J]. 洁净与空调技术, 2015(2): 33-36.
WANG Dengshan.Research on health hazard and purification technology of indoor air pollution[J]., 2015(2): 33-36.
[6] 宋英华. 红外光谱技术在环境安全领域中的应用与展望[J]. 能源与节能, 2015(08): 104-105.
SONG Yinghua.On the application and prospect of infrared spectrum technology in the environmental safety field[J]., 2015(08): 104-105.
[7] 李吉光. 在线红外结合独立成分分析研究含能化合物合成反应机理[D]. 西安: 西北大学, 2014.
LI Jiguang. Investigating the synthetic mechanism of energy compounds by on-line IR spectroscopy combined with independent component analysis[D]. Xi’an: Northwest University, 2014.
[8] 肖大为, 程锦房, 张景卓,等. 基于JADE算法的矢量水听器阵列信号盲估计研究[J]. 武汉理工大学学报: 交通科学与工程版, 2013(5): 1012-1016.
XIAO Dawei, CHENG Jinfang, ZHANG Jingzhuo, et al.Blind signal estimation based on JADE algorithm for an vector hydrophone array[J].:, 2013(5): 1012-1016.
[9] 王文涛, 张剑云, 刘兴华,等. JADE盲源分离算法应用于雷达抗主瓣干扰技术[J]. 火力与指挥控制, 2015(09): 104-108.
WANG Wentao, ZHANG Jianyun, LIU Xinghua, et al.Radar anti-mainlobe-jamming based on blind source separation algorithm of JADE[J]., 2015(09): 104-108.
[10] 宋清. 独立组分分析在光谱分析中的基础与应用研究[D]. 上海: 第二军医大学, 2012.
SONG Qing. The basic and applied research of independent component analysis in spectral analysis[D]. Shanghai: The Second Military Medical University, 2012.
[11] 边双微. 田纳西—伊斯曼化工过程的故障诊断[D]. 武汉: 华中科技大学, 2011.
BIAN Shuangwei.Fault diagnosis on Tennessee-Eastman process [D]. Wuhan:Huazhong University of Science and Technology, 2011.
[12] Cardoso J F. Higher order contrast for independent component analysis[J]., 1999, 11(1): 157-193.
[13] Cardoso J F, Souloumiac A.Blind beam forming for non-gaussian signals[J].(), 1993, 140(6): 362-370.
[14] 林继鹏, 刘君华. 光谱分析中的支持向量机方法及其性能优化[J]. 光谱学与光谱分析, 2006, 26(12): 2232-2235.
LIN Jipeng, LIU Junhua. Support vector machine and optimized method for spectral analysis[J]., 2006, 26(12): 2232-2235.
[15] 林继鹏, 刘君华. 光谱严重交叠的多组分混合气体红外定量分析技术[J].现代科学仪器, 2006(1): 53-57.
LIN Jipeng, LIU Junhua. A new technology study based on seriously overlapped spectrum of quantitative analyzing on multi-component hybrid gas[J]., 2006(1): 53-57.
Quantitative Analysis of Indoor Multi-component Gas Mixture Based on JADE
WANG Xiao1,LI Bo1,FENG Xiaoqin2
(1.,,030051,; 2.,030006,)
The infrared spectrum obtained by indoor air pollution monitor is a variety of harmful mixture gas and absorption bands of mixture gas overlap makes qualitation a difficult question. A feature extraction method based on joint approximative diagonalization of eigenmatrix (JADE) is proposed. The method can fully mine implicit information in the original data by analyzing the Higher-order statistics information so that we can separate mixture gas spectrum into each material’s spectrum. SVM (support vector machine) based on the regular theory is applied to establish a multi-dimensional data quantitative analysis model by the extracted independent source. The experimental result shows that the relevant factors of mixture gas component quantitative analysis are maintained at 0.9991, which proves the accuracy of this feature extraction method.
joint approximative diagonalization of eigenmatrix,quantitative analysis,multi-component,SVM
TM930
A
1001-8891(2016)03-0255-05
2015-10-13;
2015-12-23.
王骁(1990-),男,硕士研究生,主要研究信号处理。E-mail:valor98@aliyun.com。
李博(1972-),硕士生导师,副教授,主要研究方向为精密检测设备、信号采集与处理。E-mail:libo@nuc.edu.cn。
国家自然科学基金仪器专项基金项目(61127015)。

