多扫描周期摆镜伺服系统设计与实现

王志林，杨 帆，蒋 砾，罗志斌，朱光明



多扫描周期摆镜伺服系统设计与实现

王志林，杨 帆，蒋 砾，罗志斌，朱光明

（昆明物理研究所，云南 昆明 650223）

扫描摆镜伺服系统是扫描型热像仪的核心部件之一，扫描摆镜摆动周期需适应热像仪视频制式的要求。为了支持扫描型热像不同速率视频输出的需求，基于双向扫描摆动方式，设计并实现了多扫描周期摆镜伺服系统。给出了基于FPGA、MCU构架的硬件方案、目标轨迹特性及控制算法的设计方法。实验测试结果表明本扫描摆镜伺服系统具有跟踪精度高、频率切换时间短和运行稳定等特点，具有很强的工程实践性。

扫描摆动；双向扫描；状态反馈；前馈控制器

0 引言

基于凝视型焦平面探测器的热像仪不采用复杂的光机扫描机构，简化了系统设计[1]，但是凝视型探测器同时也具有成本较高、均匀性差[2-4]和盲元多[5-6]等缺点。扫描型探测器较之凝视型探测器由于探测元的大幅度减少，器件成本低，非均匀性处理和盲元替换易于实现，扫描型热像仪仍是红外夜视技术中极具性价比的解决方案。

扫描型探测器主要有线列（128×1）与带TDI的N系列（288×4）两类，必须采用“时间换空间”的策略，光机扫描器作为扫描型热像的重要组成部分即完成该功能[7]。光机扫描器的类型主要有：摆动平面镜、旋转镜鼓、旋转折射棱镜和旋转折射光楔等[7]，其中以摆动平面镜最为常见，也称为扫描摆镜。扫描摆镜的摆动频率和摆动方式与扫描型热像的图像帧频相关。扫描摆镜的运动轨迹主要有2种，锯齿波与三角波，锯齿波摆动即为单向扫描，三角波摆动方式也成为双向扫描。两者的特点是锯齿波的带宽较大，探测器积分区间线性度难以保证，系统设计难度大；三角波的带宽较窄，但要求探测器具有双向积分功能，并且支持积分方向的场周期切换。为了保证良好的摆动线性度，本文采用双向摆动方式进行摆镜伺服系统的设计。

区别于传统单一扫描周期摆镜伺服系统，本文设计实现多扫描周期摆镜伺服系统，在低频摆动阶段可提供较大的摆动范围，用于目标搜索；在高频摆动阶段，提供高速时间采样频率，用于追踪快速运动目标，可有效降低目标在低频采样间隙内逃逸的风险。介绍了基于FPGA、MCU构架的多扫描周期摆镜伺服组成与原理、详细分析了被控对象的组成环节，建立了准确的被控对象线性模型，并基于状态观测器与前馈校正的复合控制手段完成了算法设计。系统的特点是摆动线性度高、摆动频率切换迅速，同时可对外提供精确的摆镜轨迹相位信号，便于系统集成。

1 扫描摆镜伺服系统组成原理

1.1 系统组成

伺服系统主要由3部分组成：扫描器组件、驱动电路和运算控制电路，系统构成如图1所示。

图1 扫描摆镜伺服系统框图

扫描器组件的核心是永磁式有限摆角力矩电机和位置传感电路，可实现摆镜的驱动及位置测量并对外提供摆镜位置数据传输接口，其构成原理如图2所示。驱动电路属于控制环路中的电流环，功能是完成控制电压到控制电流的转换，并将电流控制信号输出到摆动电机，其输入电压控制信号来自运算控制电路。运算控制电路上的核心器件为FPGA与MCU，MCU内存中包含了摆镜的目标轨迹，依据FPGA在中断时刻提供的摆动频率、目标索引与摆镜的实际位置等信号，运行控制算法，输出控制电压。

1.2 软件原理说明

软件部分包含FPGA软件与MCU软件。FPGA采用低成本的Spartan6系列器件实现，时钟管理模块产生16.8MHz的工作时钟，并向MCU及其他模块提供16.8kHz周期信号；摆镜接口模块提供扫描组件接口的时钟信号，并在在检测到16.8kHz周期信号的上升沿后，产生扫描摆镜位置采样信号，进行一次位置采集与接收，将12bits的位置数据缓存，提供给MCU接口模块；索引生成模块根据摆动频率选择信号与16.8kHz脉冲信号生成目标轨迹查找表的索引号提供给MCU接口模块，并对外提供场同步信号，轨迹索引为9bits的无符号数，可给出0～511的索引号，对16.8kHz脉冲信号进行计数，并在场同步信号开始处清零。索引生成模块输出场同步信号，便于与上位系统集成，同时将摆动频率选择信号与索引信号组成一个12bits的数据发给MCU接口模块。图3显示了场同步信号、轨迹索引信号与摆动频率选择信号之间的关系以及摆镜由高频到低频、低频到高频进行切换时的各个信号与数据之间的时序关系。

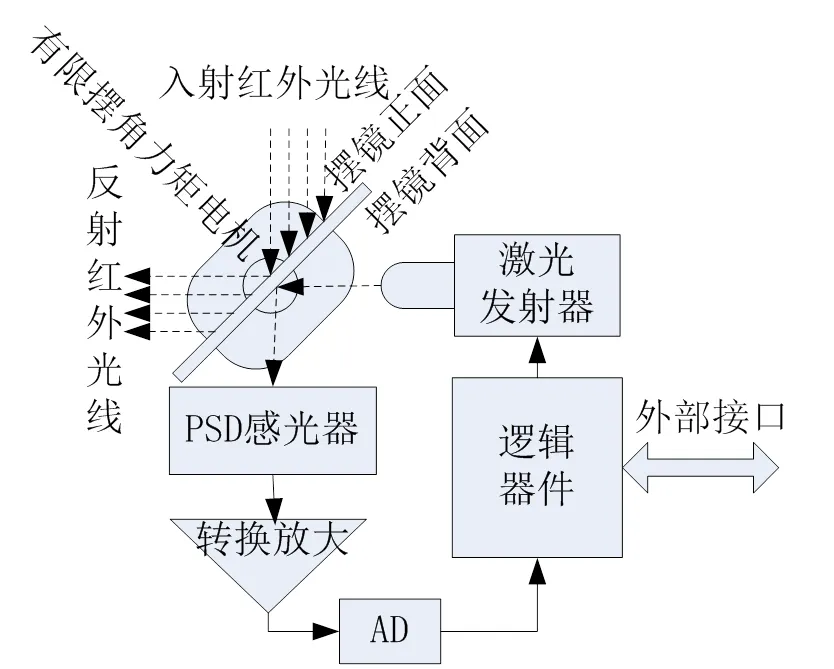
图2 扫描摆镜组件原理

图3 索引生成模块的各信号时序关系

MCU接口模块负责FPGA与MCU之间的数据传递，包含的引线有：输出到MCU的12bits的数据信号、1bit中断信号；由MCU输入的1bit数据选择信号。MCU接口模块在检测到16.8kHz的上升沿后，将索引生成模块的12bits数据挂接在MCU的数据接口上，同时向MCU发送中断信号，之后检测到数据选择信号置高后，再将摆镜接口模块提供的12bits位置数据挂接在数据接口上。

运算控制电路的MCU采用德州仪器piccolo系列的F28035实现，该型号MCU兼有小封装高性能特点，时钟上限为60MHz，支持浮点运算。MCU采用的外部时钟源频率为16.8MHz，采用控制芯片内部锁相环倍频3倍得到50.4MHz时钟作为MCU的运行时钟。中断运算频率为16.8kHz，当摆动频率为25Hz时，每个摆动周期包含的中断周期数为672，同时该数值也是25Hz目标轨迹的离散化样点数。进入到中断服务程序后，MCU首先读取FPGA发送的扫描频率与目标值索引数据，根据扫描频率信号，确定目标轨迹查找表，依据9bits的索引数据，找到查找表中的当前时刻的目标值；之后设定数据选择IO为高电平，通知FPGA输入位置反馈数据，MCU在获取了位置反馈数据后即可运行扫描控制算法，计算出控制量，发送到驱动电路；最后，程序设置数据选择IO为低电平，并清除中断标志，退出中断。

2 扫描摆镜目标轨迹与控制系统带宽

目标轨迹是扫描摆镜的跟踪轨迹，也就是在时间轴上，扫描摆镜位置传感器的位置测量数值需与目标轨迹保持一致，误差越小，则跟踪的性能越好。设计目标轨迹主要用到3个重要参数：线性区扫描速度line、线性区最大角度line以及扫描周期cyc。目标轨迹的设计原则是尽可能占据少的带宽，一方面，目标轨迹的带宽制约闭环控制系统的设计带宽b，b越小，则进入到系统的噪声越小，可提高系统抑制噪声的能力；另一方面，目标轨迹的变化越平缓，则扫描电机所需的电压与电流就越小，可有效降低功耗。本文仅给出25Hz与75Hz目标轨迹特性，具体参数如下，扫描速度：0.38°/ms；25Hz线性区最大摆角：±3.42°；75Hz线性区最大摆角：±0.95°。可以计算出扫描效率：

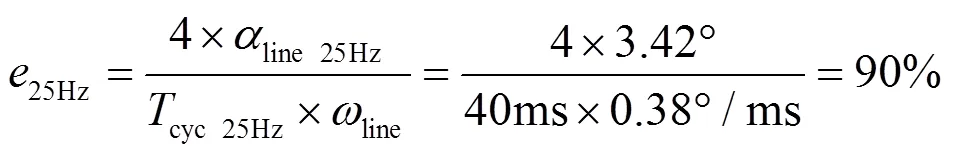
设计得到的扫描轨迹如图4。

对25Hz目标轨迹进行傅里叶级数分解[8]，得到的频谱图如图5所示。

可见随着频率的增加，幅度迅速衰减，功率集中于低频区域。仿真得出采用16（包含直流分量）条谱线即可复现25Hz目标轨迹，因此25Hz目标轨迹带宽为：

b 25 Hz＝2p×25×(16－1)＝2356rad/s

采用同样的方法可以得出采用9条谱线可复现75Hz目标轨迹，其带宽为：

b 75 Hz＝2p×75×(9－1)＝3770rad/s

闭环控制系统的带宽在满足各个目标轨迹的最大带宽需求，同时又不能过宽，否则一方面设计难度大，另一方面过大的带宽易受噪声的影响，不利于系统线性度与稳定性。

3 控制算法设计

3.1 被控对象模型

电压平衡方程表述了摆动电机输入电压到绕组电流的转换关系，由于采用了驱动电路完成电压到电流的控制，其作用相当于一个压控电流源，可以采用一阶惯性环节进行描述，如下：

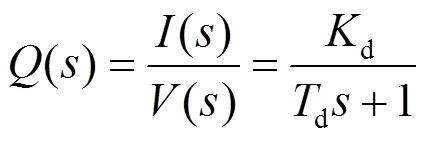
式中：d为电压到电流转换增益；d描述了转换的延时。绕组电流到输出角度之间的关系由力矩平衡方程为[9-10]：

式中：为摆镜角度，rad；为转动部件总转动惯量，kg×m2；f为速度阻尼系数，N×m×s×rad－1；t为挠性枢轴扭转刚度，N×m×rad－1；为电磁转矩，N×m。

＝Ki(5)

式中：T为电机转矩常数，N×m×A－1；为绕组电流，A。力矩方程的拉式变化如下：

可以得到被控对象的总体方程为：

即：

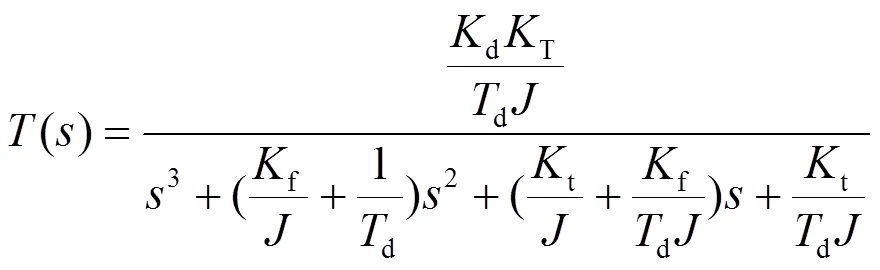
被控对象的阶跃响应特性如图6。

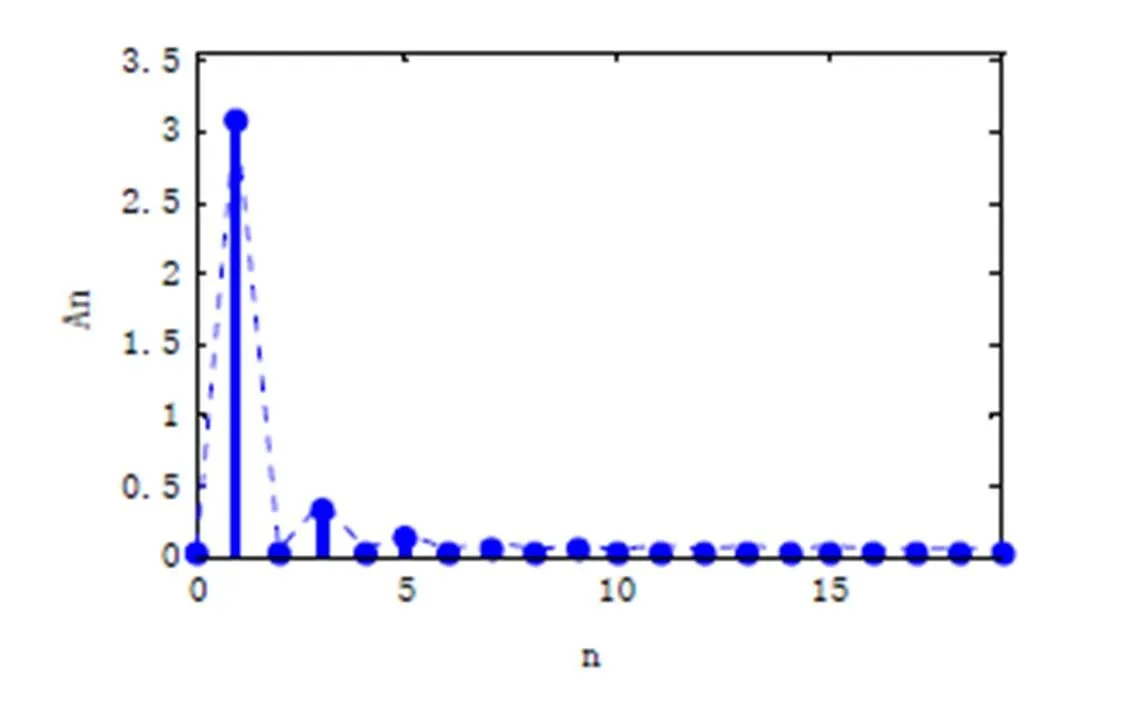
图5 25Hz目标轨迹频谱

图6 被控对象时域特性

3.2 控制器设计

在进行控制器设计时，分别尝试了PID与串联超前、滞后校正等手段[11]，但由于系统对带宽与稳定性有较高的要求，以上几种方法的设计难度较大，效果不明显。考虑到被控对象满足可控可观的要求，因此采用状态反馈的方式，对被控对象的极点进行重新分配[11-13]，之后根据稳态误差的要求设计开环增益，在满足相位裕量的前提下，尽可能取较大的开环增益。将传递函数模型转化为标准可控型状态方程：

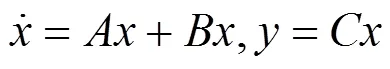
利用全维状态观测器提供的状态变量，对被控对象的极点进行重新配置：

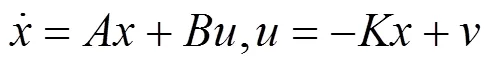
完成极点重配的被控对象称为被控系统，得到重配极点后被控系统状态方程：

(－)的特征根即为期望的新极点位置。极点位置决定了被控对象的频谱特性，极点重配的原则是使低频增益尽量大，以保证稳态误差的要求，中频段对数幅频特性的斜率一般为－20dB/dec，并占据充分的带宽，以保证具备充裕的相角裕度，高频段迅速衰减，以减小噪声的影响。较为合适的新极点位置如图7所示。

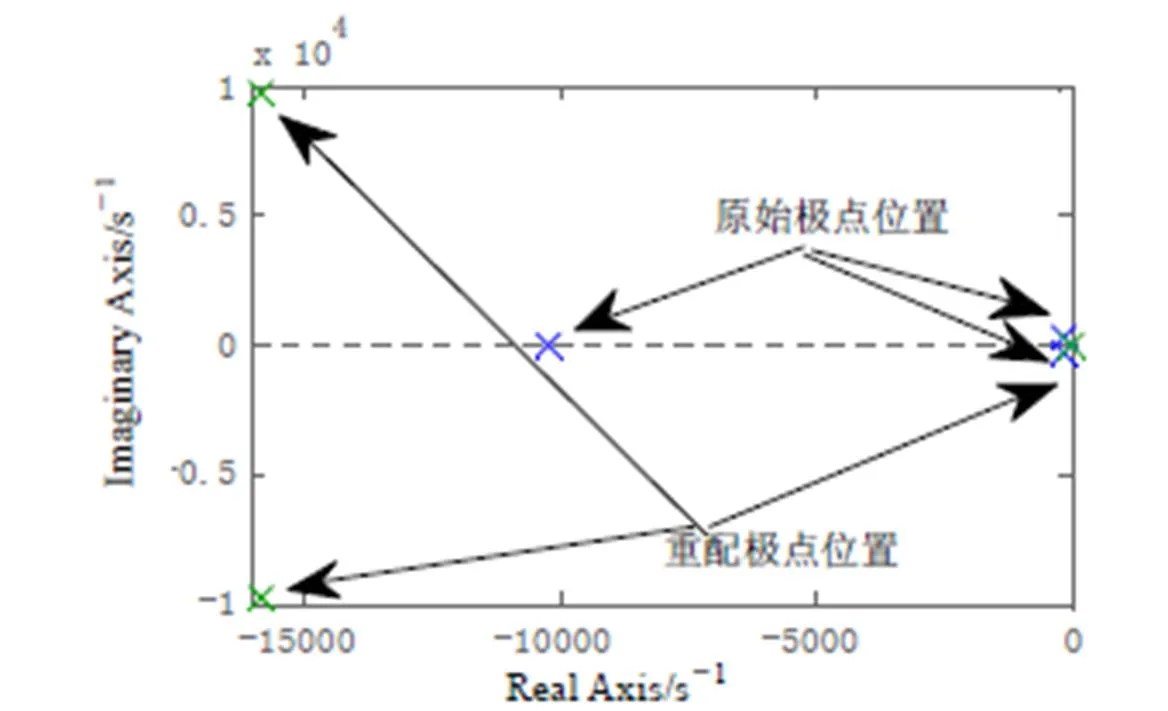
图7 极点重配

相应的开环传递函数伯德图如图8所示。

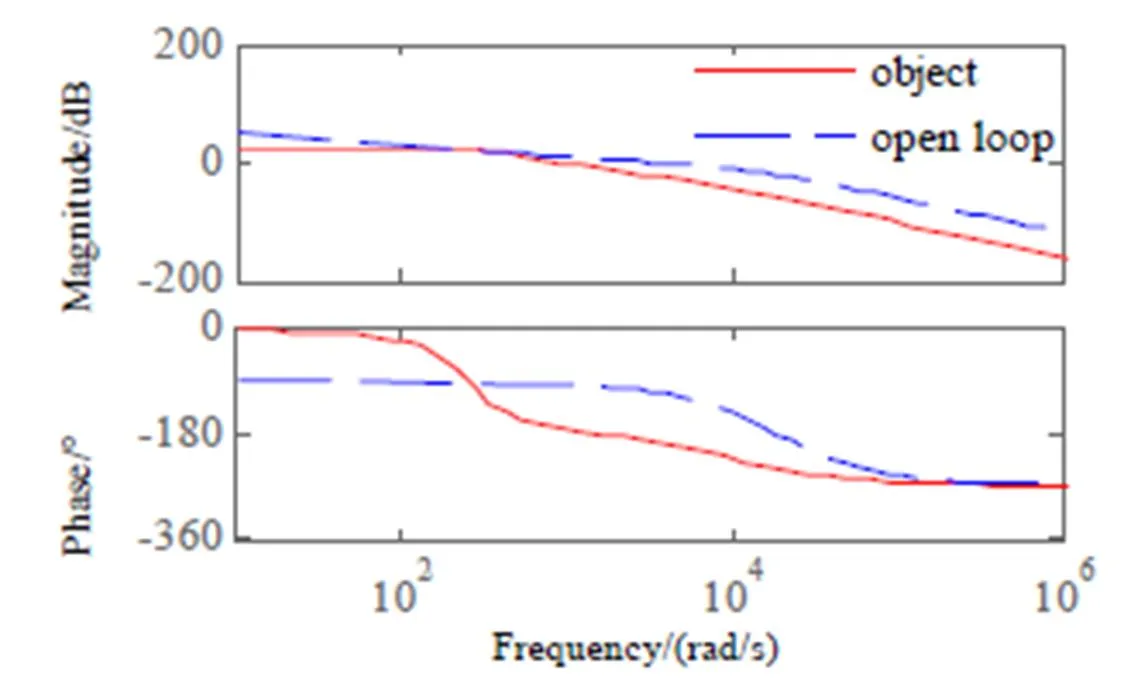
图8 开环传递函数的频率特性

最终得到的系统控制参数如表1。

表1 控制系统参数

可见系统的幅值裕度与相角裕度充分，能保证闭环系统的稳定性，同时带宽也覆盖了25Hz与75Hz目标轨迹的最大带宽要求。开环增益与系统的稳态误差相关，开环增益越大误差越小，同时也对系统稳定性造成影响，故不宜过大。有效的方法是采用前馈校正器进一步减小误差[14]，所采用前馈校正器原理如图9所示。

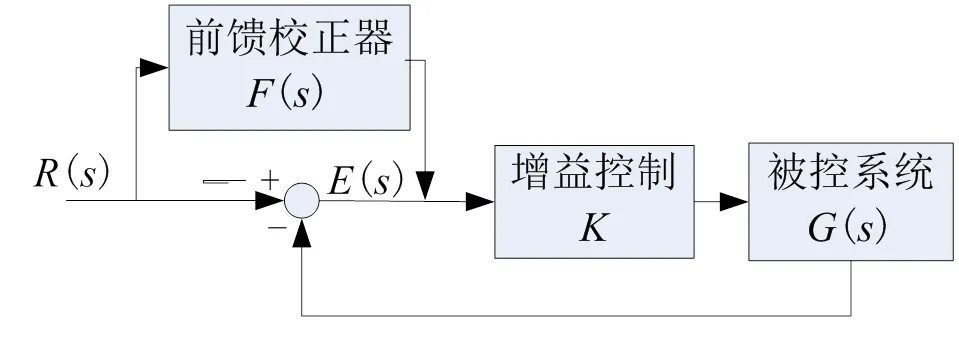
图9 前馈校正器

可以计算出输入到误差的传递函数为：

使右侧为零，则有：

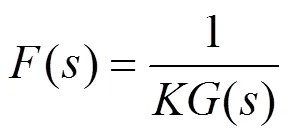
前馈传递函数实际上是被控系统的逆系统，而被控系统由被控对象极点重配得到，仍然为三阶传递函数，即()包含了常数项、一次微分项至三次微分项。由于()逆系统中常数项与三次微分项的比重很小，则简化得到前馈控制器的传递函数为：

(s)＝s＋s2(14)

式中：s相主要用于补偿轨迹线性区的误差；s2主要用于补偿轨迹非线性区误差。图10显示了被控系统有无前馈下的仿真效果对比。

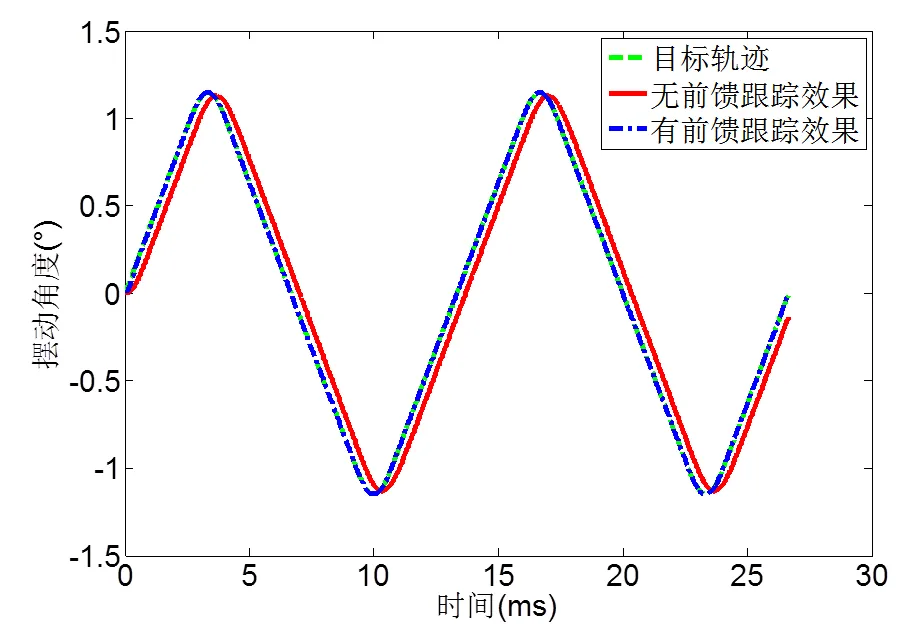
图10 前馈校正的作用

4 实现效果

将整个控制算法离散化处理后，采用C语言重新描述算法，在CCS环境下完成编译链接，生成可执行程序，并移植到MCU芯片flash中。采用示波器测量同步信号与位置测试信号，得到摆镜跟踪目标轨迹的实际效果图，图11、图12为示波器显示的25Hz、75Hz扫描模式时的摆镜位置信息与场同步信号，摆镜的跟踪特性较好，跟踪轨迹无畸变，线性区跟踪角度误差控制在（－0.005°, 0.005°）内。

图13、图14显示了摆动频率切换过程，示波器显示了切换命令信号线、摆镜位置反馈与场同步信号的变化情况。

可以看到摆镜频率切换时间极短，自收到切换命令起，会在一个当前周期时间内完成切换任务，同时，频率切换未对扫描摆镜线性度造成冲击，在切换完毕后的第一个周期即保持了良好的线性性能。

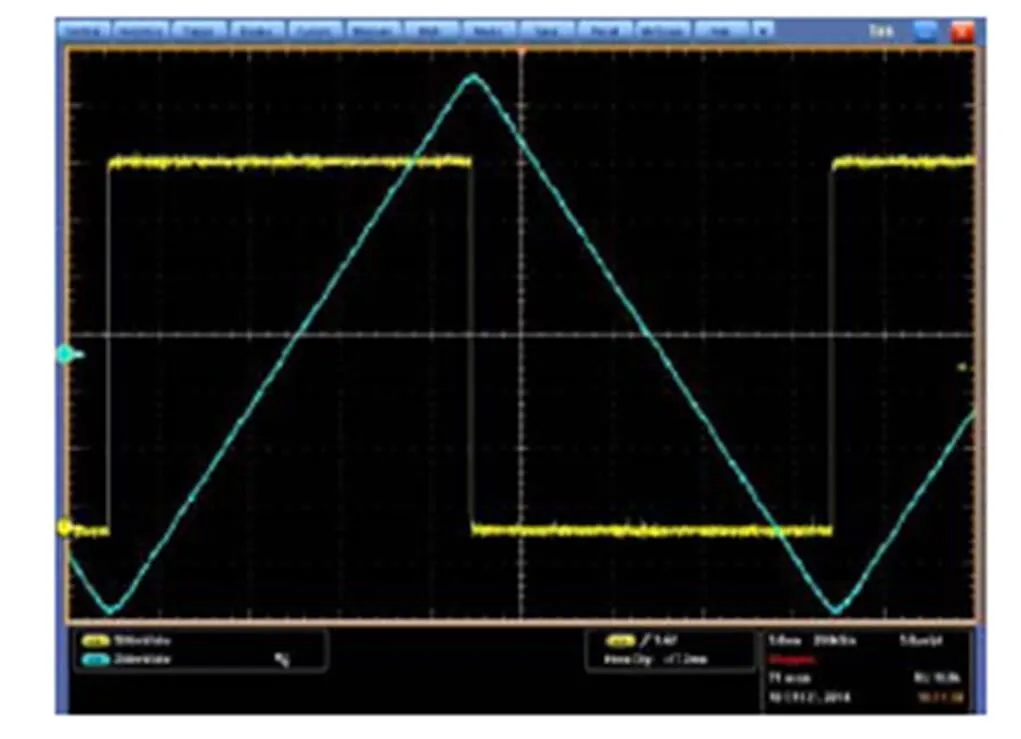
图11 25Hz摆镜位置反馈与场同步信号

图12 75Hz摆镜位置反馈与场同步信号

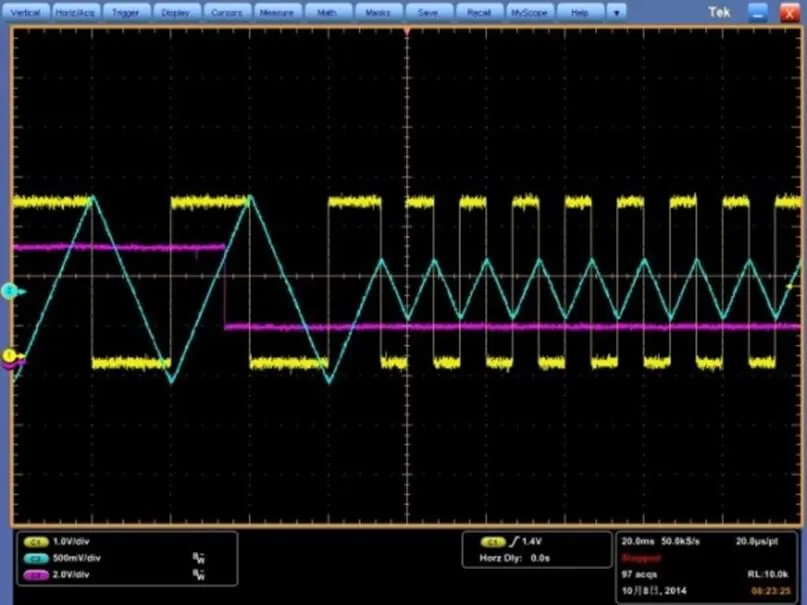
图13 25Hz扫描频率向75Hz扫描频率切换

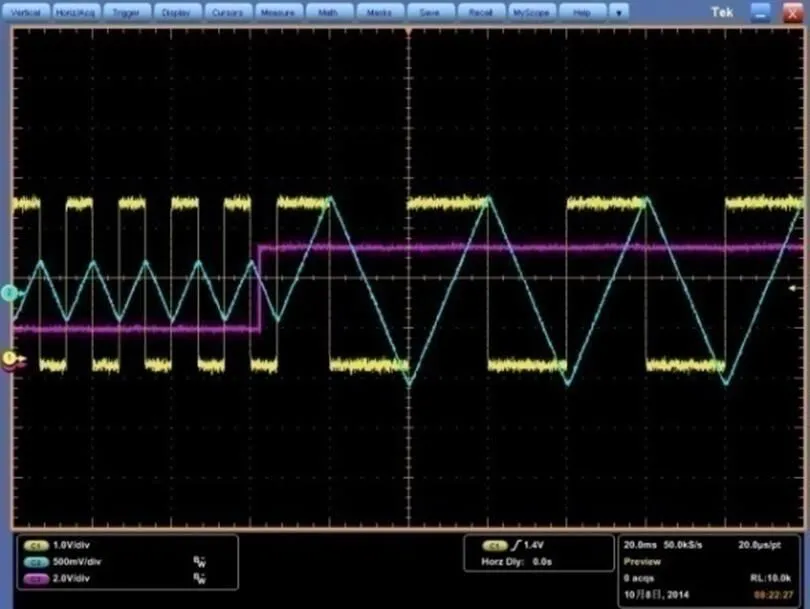
图14 75Hz扫描频率向25Hz扫描频率切换

5 结论

本文根据热像系统的实际需求，进行了多摆动周期扫描伺服系统的设计与实现，采用FPGA、MCU构架完成了接口与控制功能，结构紧凑，便于嵌入热像系统中，并且测试效果表明在跟踪精度、切换速度及抗干扰性方面表现良好。但是由于扫描器组件所提供的摆镜位置频率是固定的，进而决定了控制算法的离散化周期，粒度过粗的控制、位置采样周期不利于更高频率与更大摆角控制系统的设计与实现，因此基于更高位置采样频率的扫描器组件，依据不同的摆动频率开发变中断周期控制系统是后续研究的重点。

[1] 蔡毅. 红外系统中的扫描型和凝视型FPA[J]. 红外技术, 2001, 23(1): 3-7.

CAI Yi. The scanning and starring FPA in infrared systems[J]., 2001, 23(1): 3-7.

[2] Milton A F, Barone F R, Kruer M. Influence of nonuniformity on infrared focal plane arrayperformance[J]., 1985, 24: 855-862 .

[3] Mooney J M, Shepherd F D. Characterizing IR FPA nonuniformity and IR camera spatial noise[J]., 1996, 37(5): 595-606 .

[4] Jonathan M Mooney, Freeman D Shepherd, William S Ewing, et al. Responsivity nonuniformity limited performance of infrared staring cameras[J]., 1989, 28(11): 1151-1161.

[5] Zhang Ke, Zhao Guifang, Cui Ruiqing, et al. Method of improving bad pixel detection precision of IRFPA[J]. I, 2007, 36(4): 453-456.

[6] Jose´ Manuel Lo´ pez-Alonso,Javier Alda. Bad pixel identification by means of principal components analysis[J]., 2002, 41(9): 2152-2157.

[7] 周世椿. 高级红外光电工程导论[M]. 北京: 科学出版社, 2014.

ZHOU Shi-chun.[M]. Beijing: Science Press, 2014.

[8] Alan V Oppenheim, Alan S Willsky, Hamid Nawab S.[M]. NJ: Prentice Hall, 1997.

[9] 陈杰, 朱江, 浦文昌, 等. 高线性大摆角扫描技术研究[J]. 红外技术, 2013, 35(12): 793-797.

CHEN Jie, ZHU Jiang, PU En-chang, et al. Research on the high linearity and large swing angle scanner technique[J].2013, 35(12): 793-797.

[10] 赵建辉, 田信灵, 李帆, 等. 小角度摆动扫描控制系统的分析与实现[J].红外与激光工程, 2007, 36(3): 357-360.

ZHAO Jian-hui, TIAN Xin-ling, LI Fan, et al. Analysis and implementation of limited angle swing scanning control system[J]., 2007, 36(3): 357-360.

[11] 胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2013.

HU Shou-song.[M]. Beijing: Science Press,2013.

[12] Chen J, Prempain E, Wu Q H. Observer-based nonlinear control of a torque motor with perturbation estimation[J]., 2006, 3(1): 84-90.

[13] 郑泽东, 李永东, FADEL M.基于状态观测和反馈的伺服系统位置控制器[J].清华大学学报: 自然科学版, 2008, 48(1): 24-27.

ZHENG Ze-dong, LI Yong-dong, FADEL M. Position controller for servo systems based on state observer and feedback[J]., 2008, 48(1): 24-27.

[14] 胡庆波, 吕征宇. 全数字伺服系统中位置前馈控制器的设计[J].电气传动, 2005, 35(5): 24-27.

HU Qing-bo, Lv Zheng-yu. Feed-forward position controller design of full-digitalized servo system[J]., 2005, 35(5): 24-27.

Design and Implement of a Multi-swing Cycle Scanning Servo System

WANG Zhilin，YANG Fan，JIANG Li，LUO Zhibin，ZHU Guangming

(,650223,)

Scanning servo system is one of the core components of the scanning thermal imager. Scanning mirror swing cycle needs to adapt to the imager video system requirements. In order to meet the needs of multi-rate scanning thermal imaging video output, a multi-swing cycle scanning servo system is designed and achieved based on bi-directional swing scanning mode. This paper presents the hardware components of the servo system, characteristics of the target trajectory and the method of designing the control algorithm. With FPGA-MCU architecture, the servo system is implemented. The test results show that the servo system has the characteristics of high tracking accuracy, short frequency switching time, good stability characteristics and high practical value.

scan swing，bi-directional scanning，state feedback，feed-forward controller

TN216

A

1001-8891(2016)01-0071-06

2015-07-04；

2015-10-26.

王志林（1986-），男，满族，河北省承德，硕士，主要研究方向：光电伺服系统控制，E-mail：kwzx_wzl@sina.cn。