球面与粗糙平面电接触模型的理论分析及实验研究

瞿 航，陈 宁

（国网浙江省电力公司宁波供电公司，浙江 宁波 315000）

球面与粗糙平面电接触模型的理论分析及实验研究

瞿 航，陈 宁

（国网浙江省电力公司宁波供电公司，浙江 宁波 315000）

球面与平面接触是电触头中最常见的接触形式之一，其接触电阻的计算和分析是电触头设计过程中重点关注的。通过对工程粗糙表面进行分析，引入球面与平面接触的粗糙表面力学模型，结合经典的电接触理论，从而首次建立了球面与粗糙平面的电接触模型。并对模型进行了详细分析，定量研究了压力、塑性指数以及表面粗糙度等因素对接触电阻的影响。设计了接触电阻测量装置，对接触电阻的影响因素进行了实验测试，并对比分析理论模型计算数据和实验数据。结果表明，压力较小时，理论模型计算的接触电阻和实验数据测试较为吻合；压力较大时，理论模型有一定的局限性。

粗糙表面；接触电阻；实验测试

0 引言

电流通过接触界面时，被收缩以通过斑点，由于电流收缩产生的接触电阻称为收缩电阻，收缩电阻与金属的电阻率相关，还与接触硬度等材料表面特性相关。接触电阻包括收缩电阻和表面膜电阻，清洁表面则可以忽略金属表面的膜电阻。

接触电阻是电气连接中的关键参数，直接影响电气连接的发热与温升，进而影响电气设备的整体性能，小而稳定的接触电阻是电气连接设计的最终目标。触头的接触电阻和触头的材料、形状、接触压力以及表面状态等参数密切相关，精确且符合实际的接触电阻计算分析是触头设计的关键。

关于接触电阻的数值计算，国内外的学者做了许多研究[1-2]，提出了很多接触电阻的数值计算方法，如基于分形法描述的触头表面粗糙形貌的接触电阻数值计算方法。影响接触电阻阻值大小的电接触面积和机械接触密切相关，通过研究触头表面的机械接触可以对接触电阻进行比较真实的分析。

Li首次提出了包含弹性、弹塑性和塑性变形的粗糙表面机械接触模型[3]，并对3种变形情况下的接触压力和接触面积计算进行了总结，给出了接触压力和接触面积的通用表达式。Li的模型主要分析了平面与平面接触、球面与平面接触2种接触方式。贾丹在Li平面与平面接触模型分析的基础上，对粗糙表面的接触电阻和接触热阻进行了详细分析，并采用数值计算得到了接触电阻与表面塑性指数等的关系，对经典的电接触理论进行了对比[4]。

球面与平面接触是电触头中最常见的接触形式之一，在许多电气连接中均有运用。以下在Li和贾丹的研究基础上，结合粗糙表面力学接触模型和电接触理论相关假设，首次对球面与平面接触的接触电阻进行了理论计算。

1 电阻理论模型的建立

1.1 理论背景与假设

2个金属接触时，经典的接触电阻认为单个斑点的收缩电阻RC可以表示为[5]：

式中：ρ1和ρ2是接触金属的电阻率（文中所有分析的接触材料均为铜）；a是导电面积的半径。当接触面发生弹性变形时，在Herz弹性变形的假设下，得到接触电阻的计算式：

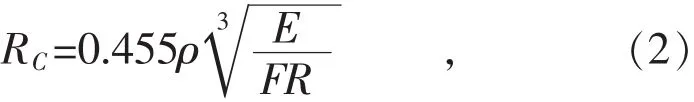
式中：F为正向压力；E为导体的杨氏模量；R为两接触表面的曲率半径。

当接触面发生塑性变形时，接触电阻可以用式（3）表示[6]：

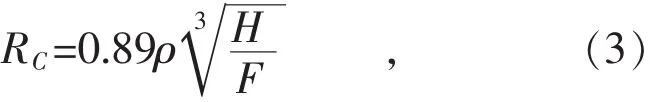
式中：H为材料的洛氏硬度。

上述接触电阻理论均假设接触表面是光滑的，未引入粗糙表面的特性参数，且认为只存在单一变形。然而任何的工程表面均是粗糙的，可以认为通常的加工表面的粗糙峰高度符合高斯分布[7]。粗糙峰高度的概率密度函数φ（z）用式（4）表示：

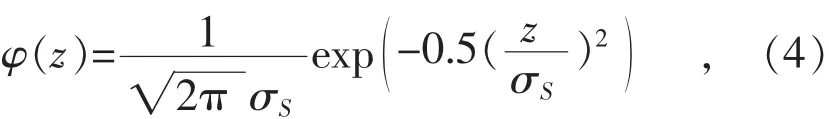
式中：z表示粗糙峰的高度；σS表示粗糙峰高度的均方差值。

可以用表面的均方根粗糙度Rq衡量σS，其和算术平均粗糙度满足

为便于分析，以下将平面假定为粗糙平面，球形表面为光滑表面。图1为光滑球面与粗糙平面接触的示意图。

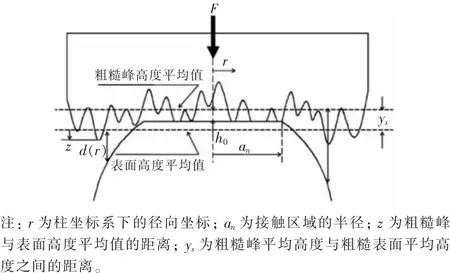
图1 光滑球面与粗糙平面接触示意

如图1所示，h（r）表示从光滑表面到粗糙峰平均高度的距离；d（r）表示从光滑表面到粗糙表面平均高度的距离。σ表示表面高度的均方差值。σs/σ和粗糙表面的特征参数β满足式（5）[9]：

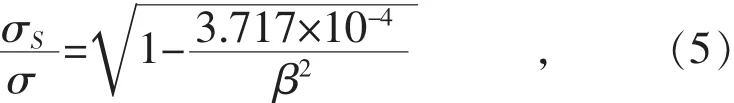
式中：β为描述表面特性的无量纲表面粗糙特性参数。β=ηρrσ，η为粗糙峰的面密度；ρr为粗糙峰的曲率半径。

假设球面与粗糙表面发生接触时，球面最高点与粗糙表面平均高度的距离为d（易知d＞0），令则在r处粗糙表面平均高度与球面的距离d（r）可用式（6）、式（7）表示：

文中的推导采用Li两粗糙表面接触理论模型的假设条件，并引入接触电阻分析中常用的假设条件[10]，模型基于以下假设：

（1）接触表面是各向同性的，接触表面的宏观基体无形变。

（2）各个粗糙峰的顶点是球形的，且有相同的曲率半径ρr，粗糙峰的高度符合高斯分布。

（3）各个粗糙峰之间有一定的距离并且不存在相互作用。

（4）粗糙峰在接触压力作用下可以发生弹性变形、弹塑性变形以及塑性变形。

（5）各个粗糙峰发生实际接触形成接触斑点的位置均导电，且各个粗糙峰之间的接触电阻没有相互作用，形成电阻并联关系。

将粗糙峰高度z进行无量纲处理，令z*=z/σ，并代入式（4）得到式（8）：

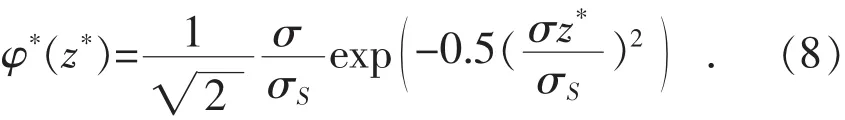
对粗糙峰的形变位移ω采用σ进行无量纲化，定义为：

由以上分析易知，只有正位移的粗糙峰才是实际接触的。通过计算单个粗糙峰的接触压力、接触面积和接触电阻，即可得到总的接触压力、接触面积和接触电阻。接触压力F、接触面积A以及接触电阻RC可由式（10）—（12）给出[11]：

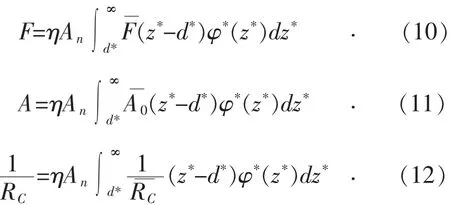
然而在电接触表面发生接触时，由于单个粗糙峰高度的差别，并不是所有表面的变形情况均一致。高度值较小粗糙峰的变形很小，可认为是完全弹性变形；高度值较大粗糙峰的变形很大，可以认为是发生完全塑性变形；粗糙峰也可能发生弹塑性变形。下面在对3种变形情况下的接触压力、接触面积和接触电阻进行分析。

1.2 模型建立

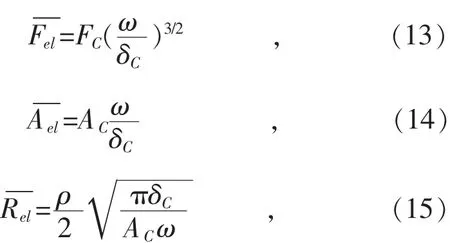
式中：FC，δC，AC分别为完全粘着条件下，光滑球体由弹性变形向弹塑性变形过渡时的临界法向作用力、临界位移、临界作用面积。

当法向位移ω满足δC＜ω＜110δC时，粗糙峰发生弹塑性变形，接触力Fep、接触面积Aep和接触电阻Rpl分别用式（16）—（18）表示[12]：

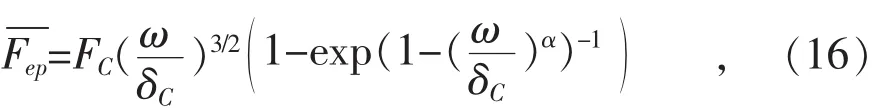
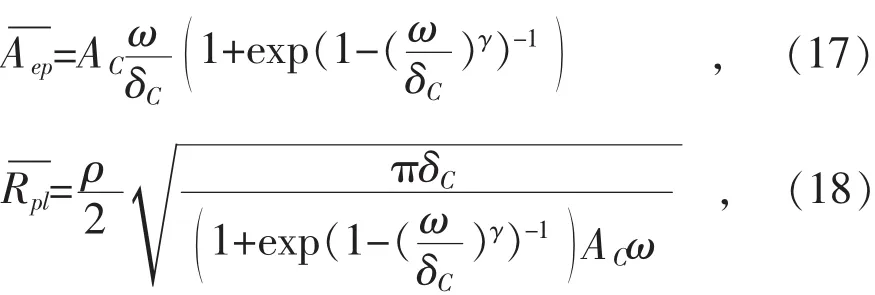
式中：α，γ为泊松比υ的函数（见表1）。此时ω＞110δC，单个粗糙峰完全塑性，Jackson和Green利用有限元仿真并拟合，得到接触力和实际接触面积的经验计算式，如式（19）—（21）所示[13]：

根据文献[10]，临界接触压力、临界位移、临界接触面积满足式（22）—（26）：

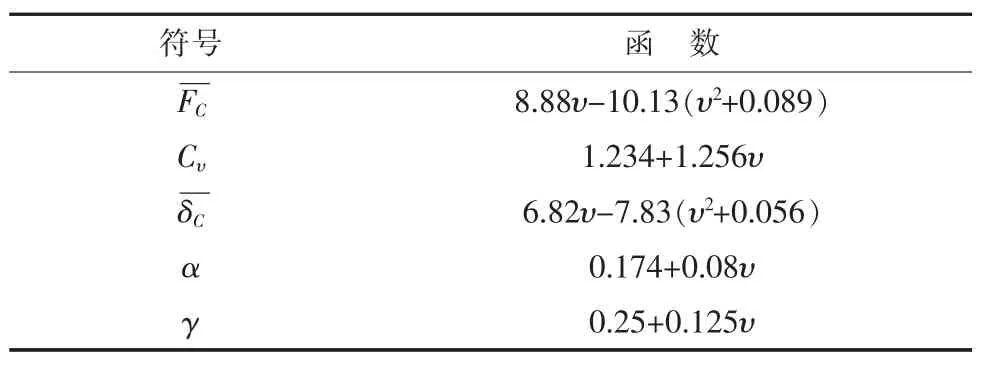
表1 泊松比函数

引入衡量表面特性的参数，塑性指数ψ。根据文献[9]，无量纲临界位移和塑性指数ψ满足关系式（27）：

结合式（25）和式（27）可得塑性指数满足式（28）：

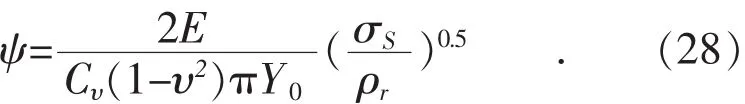
由式（28）可知，塑性指数由材料特性和表面粗糙度决定。Y0与材料的接触硬度H相关，材料硬度越小，塑性指数越大；表面越粗糙时，塑性指数越大。

引入Ig对式（25）和式（26）进行简化，令Ig满足式（29）：

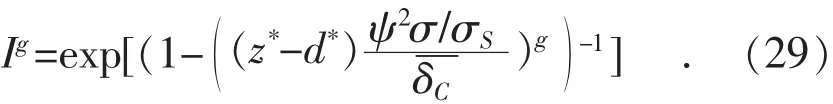
引入AC按式（30）对接触电阻进行无量纲化：

球面与平面接触时，总的接触压力、接触面积和接触电阻可以根据不同变形情况下的粗糙峰叠加而得，式（10）—（12）进一步可化为式（31）—（33）：

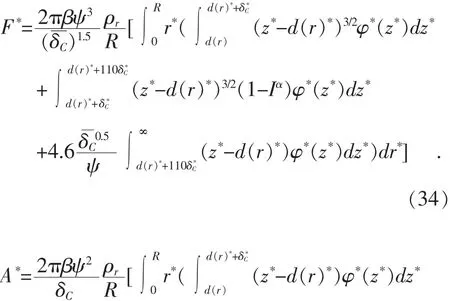
球面与平面接触时，无量纲接触压力、无量纲接触面积、无量纲接触电阻的表达式如式（34）—（36）所示。影响粗糙表面接触的无量纲接触电阻的因素有：粗糙表面的穿刺距离d；粗糙表面的特性参数 β，ρr，σS；材料参数如杨氏模量E，屈服强度Y0，泊松比υ以及接触表面曲率半径等，下文对其进行分析。

2 模型分析

式（34）—（36）均是复杂的二重积分，无法得到其具体的函数表达式。根据文献[11]，表面粗糙特性参数通常取β=0.04，微观粗糙峰的曲率半径和球面的曲率半径满足R/ρr=100。接触压力和接触面积的表达式只与塑性指数有关，而接触电阻的表达式还与接触表面的曲率半径有关。

在给定的塑性指数和表面曲率半径下，粗糙表面无量纲接触力、无量纲接触面积、无量纲接触电阻只和粗糙表面与球面的无量纲穿刺距离d*有关。应用Matlab软件，采用数值积分对公式（34）—（36）进行求解，从而得到无量纲接触压力、无量纲接触面积以及无量纲接触电阻与穿刺距离d*之间的关系。微观的穿刺距离是无法精确测量的量，而实际的接触压力则可以精确测得。接触压力是电接触过程中需要重点关注的参数，文中主要分析接触压力与接触面积、接触电阻之间的关系，以及相关参数如塑性指数、表面粗糙度对这种关系的影响。

粗糙表面的接触面积和接触压力均与塑性指数有关。通过对式（34）和（35）的数值求解，得到了塑性指数取不同值时，无量纲接触面积A*与无量纲接触压力F*的关系如图2所示。

图2 无量纲接触面积与无量纲接触压力的关系

由图2可知，在压力相同时，当表面塑性指数越小，接触面积越大；塑性指数越大时，实际接触面积越小。

对式（35）和（36）数值求解，得到塑性指数取不同值时，无量纲接触电阻与无量纲接触压力F*的关系如图3所示。

图3 无量纲接触电阻与无量纲接触压力的关系

由图3可知，塑性指数一定时，接触压力越大，接触电阻值越小。塑性指数越小，接触电阻趋于稳定的临界接触压力越小。并且塑性指数越小，稳定阶段的接触电阻越小。

接触电阻随接触压力的变化过程可以分为2个阶段，即不稳定阶段和稳定阶段。随着接触压力增大，接触电阻下降幅度较大，此时接触电阻处于不稳定阶段。接触力达到接触压力时，接触电阻减少的幅度越来越小并趋于平缓，接触电阻处于稳定阶段。

在接触电阻处于不稳定阶段时，接触电阻随着实际接触压力的增大降低。塑性指数越小（即表面越光滑）时，需要较小的作用力来增大实际接触面积；塑性指数越大（即表面越粗糙）时，需要较大的作用力来增大实际接触面积。

在实际的接触过程中，由于材料加工等原因，实际表面的塑性指数范围较小。以通常的电触头为例，常用材料为铜，表面镀银。为便于分析，忽略触头表面的银镀层。表面粗糙度在通常的加工情况下分别为0.8，1.6，3.2，6.4（单位为μm），此时塑性指数的取值分别为8.95，12.65，17.89，25.30。假设电触头接触球面的几何尺寸R=0.072 m，粗糙表面模型表面形貌及材料参数见表2。

表2 粗糙表面模型表面形貌及材料参数

通过对式（34）和（35）的数值求解，得到了不同粗糙度值时，接触面积A与接触压力F的关系如图2所示。在相同的接触压力下时，粗糙度越大，实际接触面积越小。粗糙度对塑性系数的影响较小，所以接触面积之间的差别很小，几乎可以忽略不计。通过对式（34）和（36）的数值求解，可得在不同粗糙度下接触电阻随压力的变化情况（如图4）。

图4 接触电阻与接触压力的关系

相同的接触压力下时，粗糙度越大，实际接触电阻越大，临界接触压力越大。当接触表面越光滑时，实际接触电阻越小，接触效果越理想。

根据式（2）和（3）可以得到Herz接触理论不同接触压力时的接触电阻；对式（34）和（36）的数值求解可以得到粗糙表面接触电阻模型下不同接触压力时的接触电阻。

由图4可知，Herz接触理论模型计算的接触电阻值小于粗糙表面接触电阻模型的计算值。随着压力增大，Herz接触理论模型的接触电阻值和粗糙表面模型的接触电阻值基本相同。可以认为Herz接触理论模型是粗糙表面模型的一种极限情况。

同样，由图4可知，Herz接触理论模型的临界压力小于粗糙表面模型的临界接触压力。Herz接触理论模型中，当接触压力到达临界接触压力时，实际接触表面发生塑性变形，接触压力增大，而实际接触面积基本不发生变化。粗糙表面模型中，由于粗糙表面存在多个粗糙峰，各个粗糙峰的高度不一。当接触压力增大到使较高的粗糙峰发生塑性变形时，稍低的粗糙峰与表面产生新的接触，从而增加了接触面积。只有在大部分粗糙峰都发生塑性变形时，实际接触压力才达到临界接触压力。

3 实验研究

3.1 实验概述

为了评估理论模型的正确性，测试实际工作中触头的电阻值是否和理论计算值相符。主要实验内容包括接触电阻值与压力、表面粗糙度之间的关系。

测试平台包括压力加载和测试装置、电阻测量装置以及支撑部分。根据接触电阻测量思路，设计的触头接触电阻测试装置如图5所示。

图5 接触电阻测量装置

推力球轴承的作用可以保证施力装置只给触头间施加正压力而不施加旋转力矩，保证触头在加压过程中不产生切向滑动。通过旋转上端的施力螺杆对触头施加压力。

接触电阻采用四点法测量，实验测试电流为1 000 A，采用稳态直流电流源（华泰HAP300-15）给触头供电，采用电流传感器（CHB-2KB）对电流进行测试。

当接触压力小于临界接触压力时，由于接触电阻随压力的变化比较敏感，实验压力间隔较小；当接触压力大于临界接触压力时，接触电阻随压力变化较小，压力间隔较大。触头之间的压力值可以通过压力传感器测得。

接触电阻理论计算值在30～200 μΩ，所以接触压降在30～200 mV，接触压降的测量采用Agilent 34420 A纳伏表。实验过程中，待接触压力和接触压降稳定后，读取仪器指示值并记录。

用酒精清洗接触表面，除去表面氧化膜，注意保持触点干净。在进行接触电阻测量之前，对接触表面进行粗糙度测量，测量仪器采用接触式表面粗糙度测量仪。注意表面清洗与接触电阻测量之间尽量缩短时间，防止触头表面被氧化。

在测试过程中，球面触头均采用标号1 000的砂纸进行表面打磨，以使其表面尽量接近光滑表面，对平面静触头进行不同粗糙度的打磨。

3.2 接触电阻与压力的关系

加工完成的电触头结构如图6所示。图6（a）为球面触头，图6（b）为平面触头，其表面粗糙度为Ra=0.91 μm。对单触点的电触头结构进行接触电阻测试。

图6 电触头结构

实验测试过程中，接触压力逐步从10 N增至750 N，测得接触电阻随压力的变化曲线如图7所示。由图7可知，当压力较小时，随着接触压力增大，接触电阻快速下降；当压力大于200 N时，随着接触压力增大，接触电阻基本不发生变化。最终触头的接触电阻稳定在37 μΩ左右。

图7显示，接触电阻的测量值随着压力的增大逐渐变小，最终趋于稳定的接触电阻值比粗糙表面接触模型的计算值明显偏大。原因一方面是测量时不可避免地引入了体电阻；另一方面，不是所有机械接触斑点均导电。

3.3 接触电阻与表面粗糙度的关系

触头表面按加工方式的不同，粗糙度实测值分别为0.91，1.52，3.11和6.02，测试触头的接触电阻随压力的变化情况，图8分别显示了不同粗糙度下接触电阻随压力的变化情况。

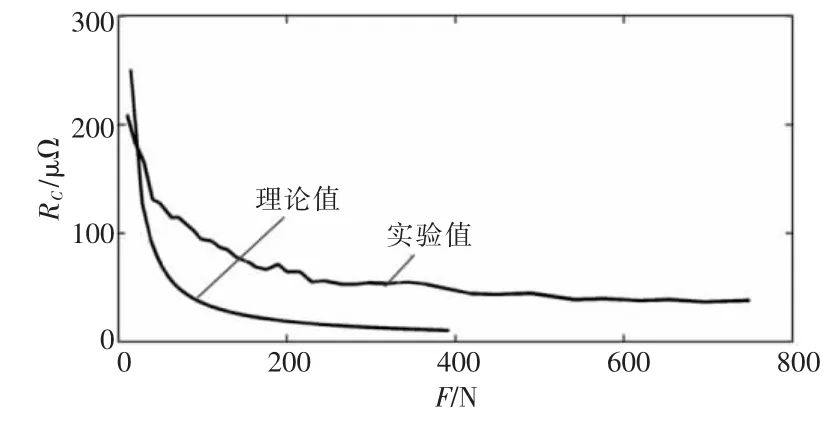
图7 接触电阻理论计算值和接触电阻测量值比较

图8 接触电阻与粗糙度的关系

由图8可知，在接触压力较小时，粗糙度越大，接触电阻越大；粗糙度越小，接触电阻越小。当压力增大时，粗糙度对接触电阻的影响很小，几乎可以忽略不计。

在理论模型中，表面粗糙度对接触电阻的影响较大，但是在实际测量过程中，仅在压力较小时粗糙度对接触电阻有影响，在较大压力时，粗糙度对接触电阻几乎没有影响。主要原因是：当压力较大时，接触部位的微观粗糙峰均发生塑性变形，各个微观粗糙峰之间由于接触压力而存在相互作用，使前述接触力学的假设不再成立。

3.4 实验分析

当接触压力较小时，接触电阻随接触压力增大有较大幅度的减小；但当触头压力较大（如大于200 N）时，接触电阻随接触压力增大只发生很小幅度的减小。实验结果同样表明，只有在较小接触压力时，表面粗糙度对接触电阻阻值有影响；当接触压力较大时，实验测试范围内的表面粗糙度对接触电阻几乎没有影响。

上述实验测试的接触电阻值比粗糙表面电接触模型的计算值略大，原因是：在接触电阻测试时引入了一部分体电阻，以及不是所有机械接触面积均导电。

通过仿真分析和实验数据的对比，提出的粗糙表面电接触模型在压力较小时能比较好地反映实际接触表面的接触电阻，有较好的实际应用价值。但是当压力较大时，接触模型几乎失效。这是因为在较大压力时，微观粗糙峰基本发生塑性变形，微观粗糙峰之间存在相互作用，上述模型的假设条件不再成立。

4 结语

在粗糙表面力学模型分析的基础上，结合经典电接触理论，首次建立了球面与粗糙平面接触的接触电阻计算模型。引入塑性参数、表面粗糙度等参量并对接触电阻进行了分析，得到粗糙表面接触电阻与塑性指数、粗糙度、压力之间的关系，并对比分析了经典电接触理论和粗糙表面电接触理论。

对接触电阻进行了实验测试，主要测试内容有接触电阻与接触压力、粗糙度之间的关系。实验结果表明，在接触压力较小时，粗糙表面电接触模型具有比较好的实用性，在接触压力较大时，粗糙表面电接触模型不再适用。

[1]谭志龙.电接触现象数值模拟的研究现状及发展趋势[J].电工材料，2010（1）∶3-8.

[2]WEIβENFELS，C P WRIGGERS.Numerical modeling of electrical contacts[J].Computational Mechanics，2010，46（2）∶301-314.

[3]LI L，ETSION I，TALKE F E.Contact area and static friction of rough surfaces with high plasticity index[J].Journal of Tribology-transactions of The ASME，2010，132（3）∶1-10.

[4]贾丹.微纳米开关多物理场复合接触研究[D].哈尔滨：哈尔滨工业大学，2011.

[5]HOLM R.Electric Contacts-Theory and Application[M]. Springer-Verlag∶Berlin，1967.

[6]张海泉.接触电阻的分析研究[J].商丘师范学院学报，2004（5）∶40-43.

[7]GREENWOOD，G A TRIPP，J H.The Elastic Contact of Rough Spheres[J].ASME Trans.J.Appl.Mech.，1967（34）∶153-159.

[8]MILENKOBRAUNOVIC，VALERYVKONCHITS，NIKOLAI.Myshkin，Electrical Contacts Fundamentals,Applica-tions and Technology[M].许良军，译.北京：机械工业出版社，2010.

[9]L KOGUT，I ETSION.A Finite Element Based Elastic-Plastic Model for the Contact of Rough Surfaces[J].Tribol.Trans.，2003（46）∶383-390.

[10]LI L，ETSION I，TALKE F E.Contact Area and Static Friction of Rough Surfaces With High Plasticity Index[J]. Journal of Tribology-transactions of The Asme，2010，132（3）∶1-10.

[11]COHEN D，KLIGERMAN Y，ETSION I.The Effect of Surface Roughnesson Static Friction and Junction Growth of an Elastic-Plastic Spherical Contact[J].Trans. ASME,J.Tribol.,2009（131）∶4-10.

[12]COHEN，D，KLIGERMAN，Y，ETSION，I.A Modelfor Contact and Static Friction of Nominally Flat Rough Surfaces Under Full Stick Contact Condition[J].Trans.ASME, J.Tribol.,2008（130）∶1-3.

[13]JACKSON R L，GREEN I.A Finite Element Study of Elasto-Plastic Hemispherical Contact against a Rigid Flat[J]. JournalofTribology，2005，127（2）∶343-354.

（本文编辑：方明霞）

Theory Analysis and Experiment Research on the Electric Contact Model in Spherical-Flat Rough Surface Contact

QU Hang，CHEN Ning

（State Grid Ningbo Power Supply Company，Ningbo Zhejiang 315000，China）

Spherical-flat surface contact is one of the most common electric contacts.Calculation and analysis of the contact resistance are the key focus in electric contact design.By analyzing the rough surface，the paper introduces a mechanical model of spherical-flat surface contact and establishes the first contact resistance model of the spherical-flat surface on the basis of the classic electric contact theory；in addition，it analyzes the model and the impact of the load，plasticity index and the influence of surface roughness on the contact resistance.A contact resistance measurement unit is designed，and the influencing factors on contact resistance are tested.In the final，the calculation data and experiment data of the theory model are compared and analyzed. The result shows that when the contact load is small，the calculated contact resistance of the theory model is coincident with the experiment data；when the contact load is high，the theory model has its limitations.

rough surface；contact resistance；experimental measurement

TM501+.3

A

1007-1881（2016）12-0036-07

2016-10-17

瞿 航（1990），男，助理工程师，从事变电运维工作。