基于业扩报装的月度负荷预测
龙厚印,刘卫东,黄锦华,李 黎
(国网浙江省电力公司经济技术研究院,杭州 310000)
基于业扩报装的月度负荷预测
龙厚印,刘卫东,黄锦华,李 黎
(国网浙江省电力公司经济技术研究院,杭州 310000)
随着我国经济进入新常态,产业结构调整加大了电力中短期负荷预测难度。采用支持向量机法、业扩增量调整法、温度调整法和K-L信息量法,充分考虑温度、经济等主导因素的影响,使用2007—2015年业扩报装数据,建立训练样本,利用历史数据检验模型的效性,并与其他方法进行比较,剖析了2016年下半年浙江省月度负荷。结果表明所选方法选取合理,预测结果相对较优。
业扩报装;支持向量机;负荷预测
0 引言
中短期负荷变化涉及具体经济走势、行业景气、消费水平,也跟气候变化及人们生活习惯有关。我国经济进入新常态,产业结构转移对负荷预测提出新的要求,很大程度上加大了负荷预测难度。常规的基于自然增长率式的分析预测已经无法适应时代发展的要求,迫切要求电力公司深入了解电力市场的内在发展变化机制,探寻其影响因素和规律性,更加科学地预测市场未来走势。
经典负荷预测方法包括产值单耗法、电力消费弹性系数法、负荷密度法、增长率法、人均电量法、分部门法等;传统负荷预测方法包括时间序列法、趋势外推法、回归分析法、灰色预测法等[1-2];新兴负荷预测方法包括专家系统法、神经网络法、SVM(支持向量机法)、模糊预测法、组合预测法等[3-7]。其中,SVM相较于其他方法对训练样本数量的要求少,预测值是恒定的,因此以下选用此方法开展负荷预测。
任何电力客户的用电必须基于一定的容量,即容量是制约客户用电需求的重要因素。容量包括存量容量和新增容量(业扩容量)。电力需求的变化由存量容量的利用变化和业扩容量的利用情况2部分共同构成。存量容量是电力市场的基础,其需求直接决定了负荷需求基值;而业扩容量则对未来负荷产生绝对影响。以下基于存量容量与业扩报装的新型负荷、电量预测方法,旨在从用电根源出发,提取销售市场不同成员的容量利用特征和业扩报装特征,揭示电力需求发展变化内因与外在驱动因素,为未来电力需求发展走势提供科学的判断依据。
1 模型简介
1.1 实际业扩增量提取
业扩报装容量对电力负荷的影响存在滞后性,当月业扩报装容量与当月的负荷情况没有直接的联系。应考虑如何求取对当月负荷具有实际影响的业扩报装增量。
假设负荷稳定月份为n个月,第k月的业扩申请容量为Uk,逐月负荷投运比例为a1,…,an,则第k月的业扩申请容量对第j月有影响的实际业扩容量yj满足式(1):
yj=Ukaj-k+1,k≤j≤k+n-1 . (1)
比如负荷稳定月份为n=3个月,逐月负荷投运比例为a1,a2,a3,用户在1—4月的业扩申请容量分别为U1,U2,U3,U4,则实际业扩增量如表1所示。

表1 各月份实际业扩增量
将7种业扩报装业务在该月的业扩增量进行累加,即为影响当月负荷的实际业扩增量。
1.2 负荷主导因素辨识
负荷需求的变化受众多外在因素的影响,在此研究了经济环境、主导行业发展产业链、上下游相关行业等影响浙江电力市场的外在相关因素,并进行大范围的外部数据收资。不同因素对负荷的影响程度不同,将所有因素都列入考虑范围来修正负荷既不现实也降低了计算效率,所以需要量化各因素的影响,筛选出和负荷关联较大的影响因素。利用K-L信息量法,定量分析影响因素,并求出其中的主导因素。
1.3 SVM理论
SVM法受到了国际学术界重视,并广泛用于解决分类和回归问题。在处理非线性问题时,SVM首先将非线性问题转化为高维空间中的线性问题,然后用一个核函数来代替高维空间中的内积运算,从而巧妙避免了复杂计算问题,并且有效克服了维数灾难及局部极小问题。
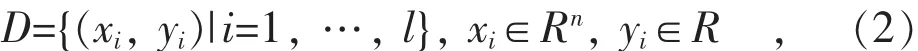
SVM回归算法中假设样本数据D如式(2)所示:式中:i为样本数;xi为输入变量;yi为输出变量。则通过SVM来回归得到函数f(x),满足由该函数得到的输出值与实际输入样本的输出变量相差不超过一定偏差,同时要求该回归函数尽量的平滑。
目前在回归问题中使用较多的是ε-SVR(ε型支持向量回归),它首先定义了不敏感损失函数如式(3)所示:
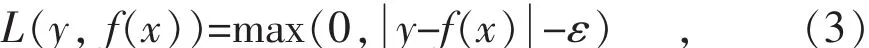
式中:ε为不敏感损失系数。该式表示在函数f(x)值的上下各设定宽度为ε的不敏感区域,当实际值y落在该区域以内时不计及误差损失。
当样本数据为线性关系时,回归函数用式(4)表示:

式中:ω为权值向量;b为常数。
对于非线性关系的情况,SVM构造出一个映射φ(x),把样本的输入变量xi从原空间Rn映射到高维空间Rm(m>n)中,使得映射后的样本数据{(φ(xi),yi)}满足线性关系。这里将输入变量映射成自身也加入映射φ(x),则高维空间Rn变为高维空间Rm(m>n)。此时不管样本数据为线性还是非线性,其回归函数都可以用式(5)表示:

根据结构风险最小化原则,ε-SVR的目标函数为:
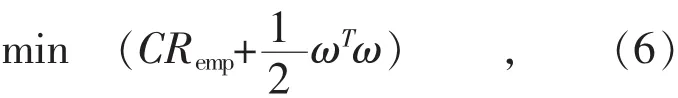
式中:C>0为惩罚参数。式(5)的前一项代表了经验风险,其值通过不敏感损失函数式(3)计算;后一项代表了函数集合的复杂度。两者之间的数值关系由惩罚参数C来平衡。惩罚参数越大,表明经验风险对目标函数的影响越大,也就是越看中回归函数的训练误差。
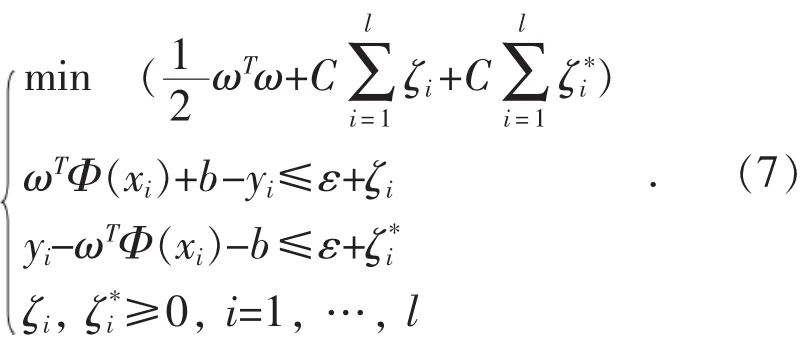
引入Lagrange函数,并利用对偶原理可以得到式(7)的对偶最优化模型如式(8)所示。
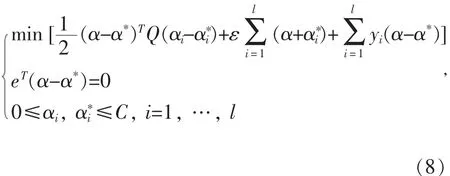
求解以上二次优化问题,进而得到回归方程的解:
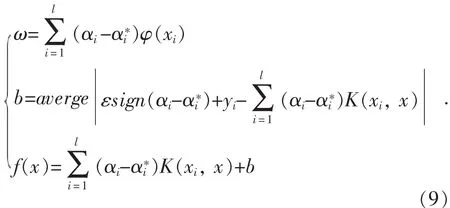
2 研究步骤
采用SVM开展负荷预测的具体步骤如下:(1)根据业扩报装的容量和逐月影响比例,计算每个月的实际业扩增量,并作为样本。
(2)收集与负荷相关的影响因素数据,采用K-L信息量法选取影响负荷的主导因素,并加入样本。
(3)构建训练样本,每个样本集输出为预测月负荷数据,输入为影响该月的因素,并对负荷数据进行气温修正。
(4)对数据进行归一化处理。归一化的目的是将输入向量中的各属性之间的数量级拉近,避免因量级相差过大而致使预测失真。首先要确定输入向量各属性数据的最大值ximax和最小值ximin,然后利用式(10)将数据归一化到[0,1]之间。
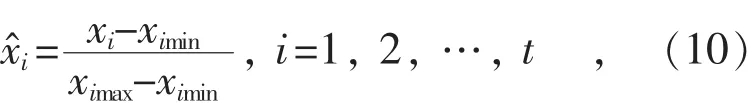
式中:t为输入向量中属性的个数。
(5)根据新建样本,利用智能算法寻找最优参数。
(6)将最优的参数赋值给SVM预测模型,得到决策回归方程。
(7)建立与表1类似的预测样本,将预测样本输入值代入决策回归方程,再将输出值进行气温调整,从而获得预测结果。
3 结果检验
利用浙江省2007—2014年统调月最大负荷历史数据验证负荷预测模型的有效性。将负荷数据分成2部分,以2007—2013年数据作为训练样本,代入基于SVM的负荷预测模型进行建模;以2014年的数据作为基准,与预测的负荷数据相比较,来判断模型的有效性。
(1)提取统调月最大负荷的主导因素。选用的影响因素分为3大类,其中经济形势包括GDP和人均GDP,产业结构包括一、二、三产的GDP产值和一、二、三产的GDP比重,其他因素包括固定投资资产和工业增加值。其中,GDP的数值由平减指数转化为2005年人民币不变价以便比较。另外,由于GDP数据只以每季度形式发布,为了与每月的最大负荷进行比较,将每月的GDP用当季度GDP数值进行代替。最后通过K-L信息量法计算的结果如表2所示。
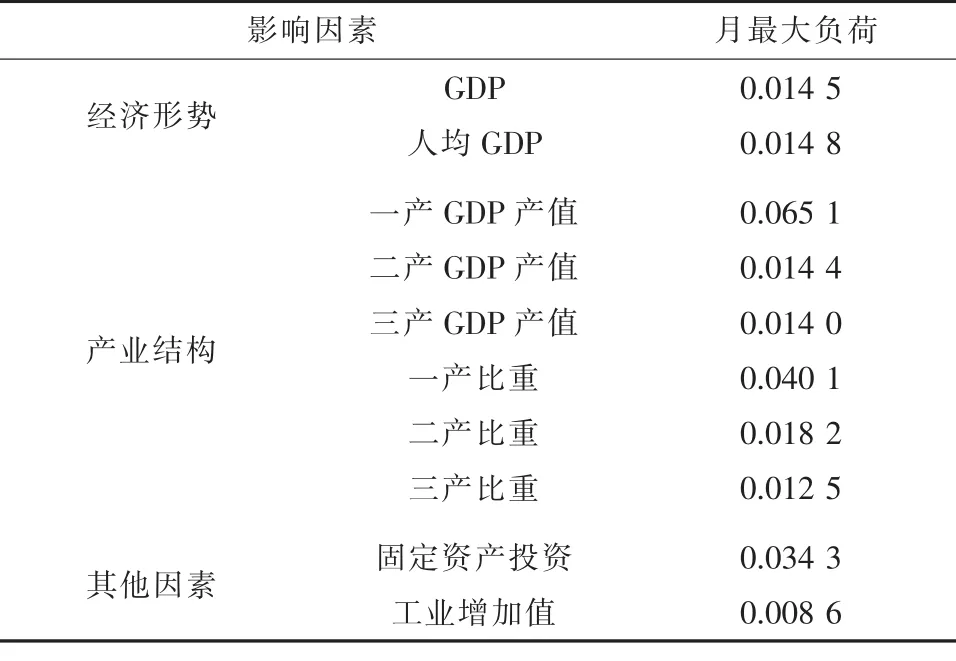
表2 统调月最大负荷K-L信息量
由表2可知,K-L信息量较低的影响因素有GDP、人均GDP、二产以及三产的GDP产值和GDP比重、工业增加值。在各影响因素中,工业增加值的K-L信息量远远低于其他影响因素,仅为0.008 6,这说明统调月最大负荷的变动与工业增加值的联系最大,则可以认为工业增加值是影响统调月最大负荷的主导因素。
(2)对负荷进行气温影响修正。以9月份的负荷数据为例,修正结果如图1所示。可以看出:2012年9月的平均最高气温较总体水平低1℃,而2013年则高1℃。这使得2011—2014年9月的负荷变化出现波动,2012年负荷低于2011年,而2013年负荷相对2012年大幅上升,并高于2014年。气温影响修正之后,可以看到9月份的负荷符合常规的增长趋势。
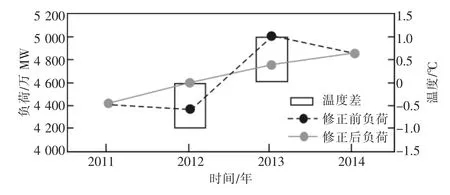
图1 9月份负荷气温影响修正
SVM模型的固定参数设置如下:SVM类型选择epsilon-SVR;核函数选择高斯径向基核函数;损失函数参数选择0.01,即误差小于0.01,则认为没有误差;交叉验证参数选择3;其余参数需要根据样本数据自动寻优。将2007—2013年数据代入负荷预测模型,得到SVM模型自动寻优后的最优参数如下:高斯径向基核函数参数为3.9;惩罚函数参数为3。
(3)结果比较。2014年月度负荷预测数据和实际数据如表3所示,可见负荷预测值和实际值比较接近,相对误差都在6%以内,其整体的平均相对误差为2.4%,因此建立的基于SVM的负荷预测模型能有效预测未来负荷数值,且精度较高。
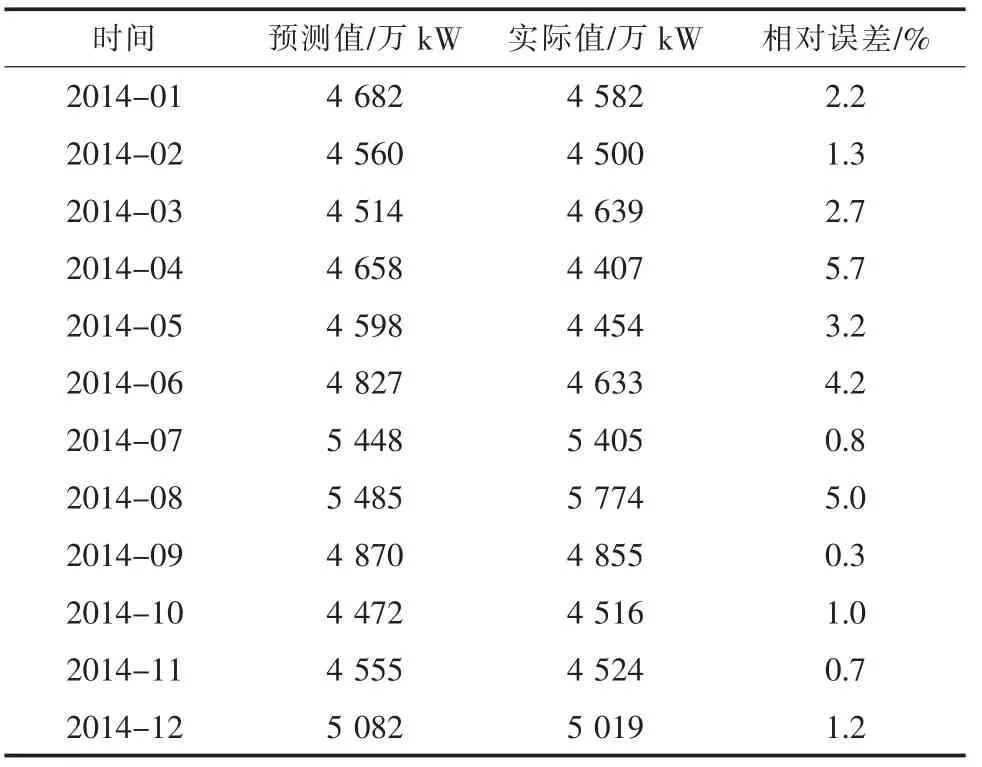
表3 误差分析
为了验证该方法的优势,将其与其他传统预测方法进行比较,对比结果见表4和表5。可以看出:考虑影响因素的SVM法无论是平均相对误差还是最大相对误差均比较占优,并准确预测出2014年的最高负荷在8月出现。对比SVM和BP(神经网络)模型的预测结果,同样SVM模型无论是平均相对误差还是最大相对误差均低于BP模型。上述结果表明:SVM模型泛化能力更强,预测精度更高。
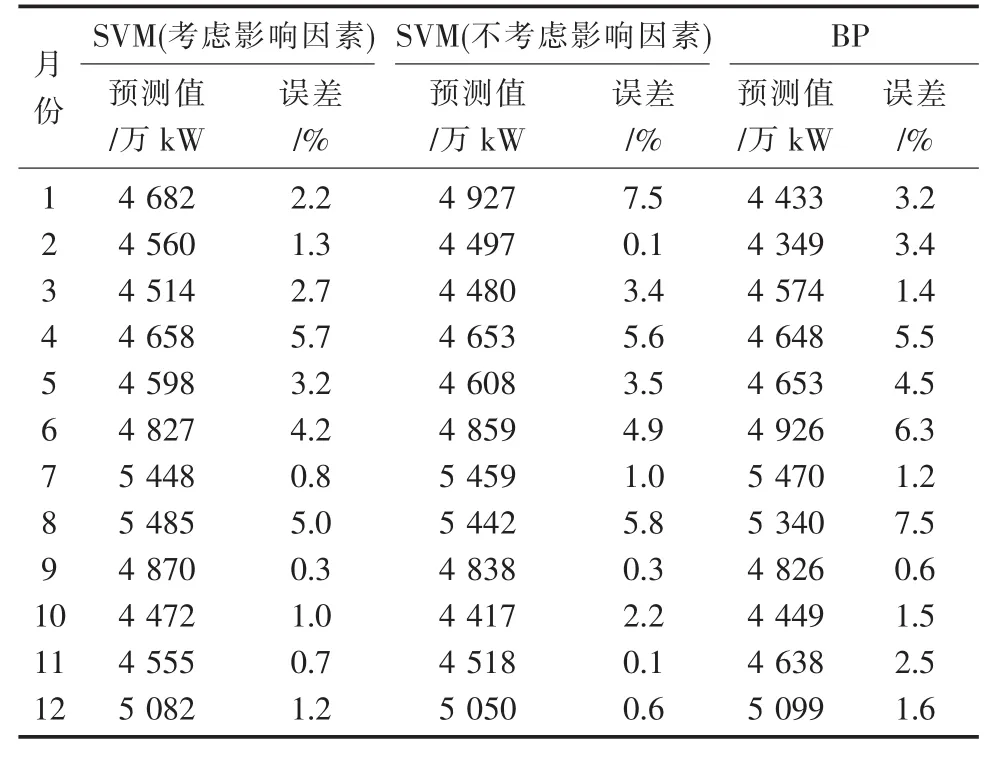
表4 不同方法预测结果
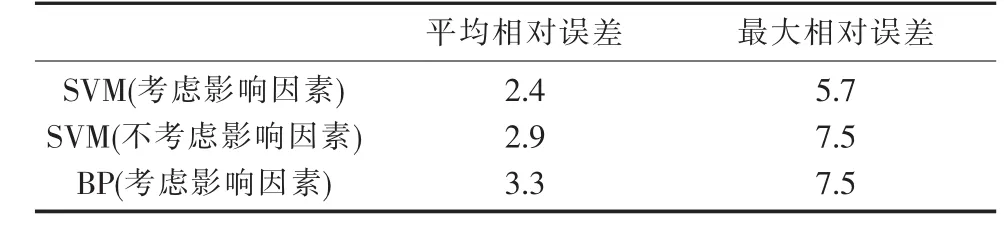
表5 不同方法预测精度分析%
4 负荷预测
利用历史数据为训练样本,预测得到浙江省2015—2016年的统调月最大负荷如表6所示。预计2016年的统调最大负荷在8月,为5 911万kW,同比增长2.6%。

表6 2016年下半年预测负荷万kW
5 结语
深入考虑目前经济形势和产业结构调整对中短期负荷的影响,使用SVM法,利用微观大用户数据,探讨2016年下半年负荷预测问题。研究表明SVM法优于其他短期负荷预测模型,负荷预期结果为:2016年的统调最大负荷在8月,为5 911万kW,同比增长2.6%。
[1]刘晨晖.电力系统负荷预报理论与方法[M].哈尔滨:哈尔滨工业大学出版社,1987.
[2]王锡凡.电力系统规划基础[M].北京:中国电力出版社,1994.
[3]李春祥,牛东晓,孟丽敏.基于层次分析法和径向基函数神经网络的中长期负荷预测综合模型[J].电网技术,2009,33(2)∶99-104.
[4]何川,舒勤,贺含峰.ICA特征提取与BP神经网络在负荷预测中的应用[J].电力系统及其自动化学报,2014,26(8)∶40-46.
[5]刘文颖,门德月,梁纪峰,等.基于灰色关联度与LSSVM组合的月度负荷预测[J].电网技术,2012,36(8)∶228-232.
[6]吴钰,王杰.基于加权最小二乘支持向量机的月度负荷预测[J].水电能源科学,2012,30(5)∶174-177.
(本文编辑:方明霞)
A Monthly Load Forecasting Method Based on Business Expansion and Installation
LONG Houyin,LIU Weidong,HUANG Jinhua,LI Li
(State Grid Zhejiang Economy Research Institute,Hangzhou 310000,China)
With China′s economy entering a new normal,industrial restructuring makes medium and shortterm load forecasting more difficult.The paper adopts support vector machine method,business expansion and installation adjustment method,temperature regulation method,K-L information and completely takes important influencing factors including temperature and economy into account;besides,it uses business expansion and installation data from 2007 to 2015 to acquire training sample and compares with other methods to analyze monthly load in Zhejiang province in the second half of 2016.The result implies that the methods are reasonable and superior in prediction.
business expansion and installation;support vector machine;load forecasting
TM715+.1
B
1007-1881(2016)12-0011-04
2016-10-17
龙厚印(1985),男,工程师,从事电网规划工作。

