定量危害性矩阵分析方法研究

王锦妮，火建卫

(中国航空工业集团公司 第一飞机设计研究院，西安　710089)



定量危害性矩阵分析方法研究

王锦妮，火建卫

(中国航空工业集团公司 第一飞机设计研究院，西安710089)

摘要：危害性矩阵分析中，由于同一个严酷度类别在矩阵图中是一个区间，容易出现当几个故障模式的严酷度相同时，在矩阵图中无法精确标识，从而使得得出的危害度有偏差。同时，利用作图法，分析效率较低。本文首先对目前的危害性分析方法进行改进，将区间进行再次划分并用显性直观的数值进行度量；然后，以某型飞机升降舵操纵分系统为例，进行危害性分析。结果表明：该方法可以对各故障模式或产品的危害度给出精确的量化值，为改进决策提供支持。

关键词：故障模式、影响及危害性分析；危害性矩阵；危害度

0引言

故障模式、影响及危害性分析(Failure Mode, Effect and Criticality Analysis，简称FMECA)是分析产品所有可能的故障模式及其可能产生的影响，并按照每个故障模式产生影响的严重程度及其发生概率予以分类的一种归纳分析方法，是一种单因素的分析方法。FMECA由故障模式及影响分析(Failure Mode and Effect Analysis，简称FMEA)和危害性分析(Criticality Analysis，简称CA)两部分组成，CA是FMEA的补充和扩展[1-2]。

FMECA是产品可靠性分析的一项重要的工作项目，也是开展维修性分析、安全性分析、测试性分析和保障性分析的基础。大多数的复杂系统在使用过程中一旦出现故障，由于故障模式的多样性，影响不确定性高，危害度往往超出人们的预期。因此，对危害性大的故障模式进行排序，进而根据排序结果进行改进设计显得极其重要。

针对FMECA风险评价和排序方法的研究主要集中在模糊数学方法的处理上，John B.Bowles等[3]将模糊数学引入到危害性分析中，提出了基于模糊理论的FMECA评价方法。崔文彬等[4]利用模糊理论对影响故障模式危害性的各因素进行了模糊处理，建立了故障模式危害性评定的模糊评判模型，阐述了模糊评判方法的基本步骤。刘娜等[5]提出了基于故障发生频率、严重程度以及检测难度三因素的模糊危害度评价模型，以评分方式解决实际工作中精确值难以获取的困难。以上方法从不同的角度提出了危害度的度量模型，但并没有解决采用传统的定量危害性矩阵分析时，在危害性矩阵图中如何精确描述和确定代表某个特定故障模式点的位置。

通常，故障模式点纵坐标的确定方法是明确的，但其横坐标的确定方法不清晰，缺少指导依据和参考标准。同时，利用作图法，存在较大的误差。为了解决上述问题，本文对目前的危害性分析方法进行改进，将每个等级的严酷度又划分为5个层次，并用显性直观的数值进行度量，然后以某型升降舵操纵分系统为例，进行实例验证，以期有效解决精确度和效率低的问题。

1定量危害性矩阵分析方法

1.1绘制危害性矩阵图的目的和方法

(1) 目的

比较每个故障模式影响的危害程度，为确定改进措施的先后顺序提供依据。危害性矩阵是在某个特定严酷度类别下，对每一个故障模式危害程度或产品危害度的结果进行比较，危害性矩阵与风险优先数一样具有指明风险优先顺序的作用[6]。

(2) 方法

横坐标一般按照等距离表示严酷度类别(Ⅰ、Ⅱ、Ⅲ、Ⅳ)；纵坐标为产品危害度、故障模式危害度，或故障模式发生概率等级(采用定性分析方法时)。其方法是：首先按照产品危害度、故障模式危害度的值或故障模式发生概率等级在纵坐标上查到对应的点，再在横坐标上选取代表其严酷度类别的直线，并在直线上标注产品或故障模式的位置(利用产品或故障模式代码标注)，从而构成产品或故障模式的危害性矩阵图[7-8]，即得到各产品或故障模式危害性的分布情况。

1.2危害性矩阵图的应用

危害性矩阵图如图1所示。从其中所标记的故障模式分布点向对角线(虚线0P)作垂线，以该垂线与对角线的交点到原点的距离作为度量故障模式(或产品)危害性大小的依据，距离越长，其危害性越大，即越应优先采取改进措施[9]。在图1中，因0-1距离比0-2距离长，则故障模式M1比故障模式M2的危害性大。当采用定性分析时，大多数分布点是重叠在一起的，此时应按照区域进行分析。

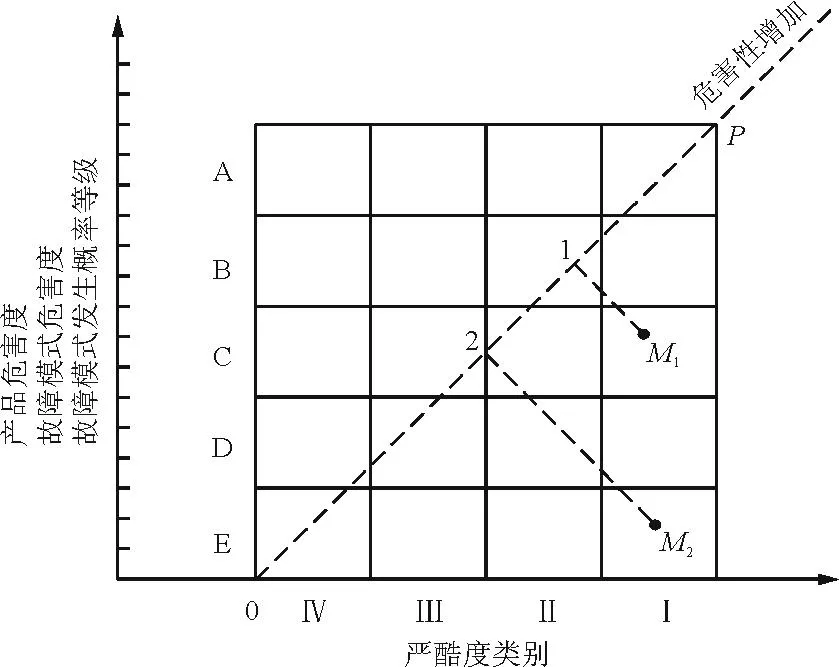
图1　危害性矩阵图

定量危害性矩阵分析方法主要是按照相关公式分别计算每个故障模式的危害度和产品危害度，并对求得的不同产品危害度和故障模式危害度的值分别进行排序，或应用危害性矩阵图对每个故障模式的危害度和产品的危害度进行危害性分析。

1.2.1故障模式的危害度

故障模式的危害度是产品危害度的一部分。计算产品在工作时间t内，第j个故障模式发生的某严酷度类别下的危害度(Cmj)，计算公式为

Cmj=αj×βj×λp×t

(1)

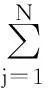
1.2.2产品的危害度

产品危害度(Cr)是该产品在给定的严酷度类别和任务阶段下的各种故障模式危害度之和。

(2)

1.3危害性分析的实施

CA的实施与FMEA相同，采用填写表格的方式进行，CA表中的故障模式编码应该与FMEA表中的一致。典型的CA表如表1所示。

表1　CA表

第(1)～(7)栏的内容与FMEA表中对应栏的内容相同；在第(8)栏记录危害性分析时所采用的故障数据(含故障率数据和故障模式频数比数据)来源，当采用定性危害性分析方法时，此栏记录故障模式概率等级；第(9)～(14)栏记录危害度计算的相关数据及计算结果；第(15)栏记录对其他栏的注释和补充。

2定量危害性矩阵分析方法的不足

在现有的FMECA指导标准、可靠性工程手册和参考资料中，关于定量危害性矩阵分析方法的内容基本相同。在工程应用中，进行定量危害性矩阵分析时，均参照GJB/Z1391-2006或型号可靠性工程手册中的方法，现阶段的定量危害性分析方法存在以下不足：

(1) 严酷度类别在矩阵中无法精确标识

利用危害性矩阵图进行定量危害性分析时，要在危害性矩阵图确定代表某个故障模式点的位置。代表某个故障模式点的纵坐标依据产品危害度或故障模式危害度的值确定，纵坐标的确定方法清晰明确。但是，危害性矩阵中图中的横坐标一般按等距离表示严酷度类别(Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类)，对于Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类严酷度类别，在危害性矩阵图的横坐标上分别是四段线段，对于严酷度类别已确定的某个故障模式，如何在对应的线段上确定代表该故障模式点的横坐标(确定代表某个故障模式的点在横坐标轴上的位置)，缺少指导依据和参考标准。

目前在工程应用中进行定量危害性矩阵分析时，对于代表某个故障模式点的横坐标，在危害性矩阵图中，通常仅要求将其确定在与其严酷度类别相对应的线段范围内即可，这样的处理方式影响定量危害性矩阵分析结果的准确性。

(2) 手工绘图误差大、效率低

定量危害性矩阵分析方法是一种手工绘图分析方法，绘图测量的方法存在作图误差，分析时先确定代表各个故障模式的点在危害性矩阵图上位置，测量这些点在危害性矩阵图对角线上的垂足(垂直投影点)与原点之间线段的长度，依据垂足点与原点之间线段长度值进行大小排序，比较故障模式(或产品)危害性，为确定产品改进措施的先后顺序提供依据。

FMECA要结合产品设计状态的更新迭代进行，危害性矩阵分析也应进行迭代。当产品的的设计状态变化较频繁、产品的故障模式较多时，定量危害性矩阵分析的手工绘图、测量分析方法的工作效率低。

3定量危害性矩阵分析方法的改进

3.1故障模式横坐标的确定

严酷度类别是对故障模式导致最坏的潜在影响的一种度量，严酷度类别的划分应依据故障模式对“初始约定层次”最终可能出现的人员伤亡、任务失败、产品损伤(或经济损失)和环境损害等方面的影响程度进行确定的。在研究危害性矩阵图中代表某个故障模式点横坐标的确定方法时，既要考虑不同严酷度类别的的差别，还应考虑相同严酷度类别的不同故障模式，其最终影响的严酷程度可能会有差别。产品的FMEA报告中有明确的严酷度类别及定义，工程中常用的严酷度类别划分为：Ⅰ类(灾难的)、Ⅱ类(致命的)、Ⅲ类(中等的)、Ⅳ类(轻度的)，若将Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类看成评分的分数值，这种严酷度类别的划分方法是一种评分法。

进行定量危害性矩阵分析时，用Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类的严酷度类别划分方法，不能准确地确定代表故障模式的点的横坐标，需要定义可操作性好的评分规则，便于用数学方法进行处理，方便在危害性矩阵图上确定代表某故障模式点的横坐标数值，以提高定量危害性矩阵分析结果的准确性。

为了提高分析的效率和精度，将Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类的对应评分划分为5档，另外，考虑要在同一坐标系反映，因此，分别对应20-16,15-11,10-6，5-1，每档的5个整数，分别对应于导致某类严酷度的可能性，由高到低依次为“绝对会导致”、“肯定会导致”、“一般会导致”、“有可能会导致”、“导致该类严酷度的可能性很低”。

本文推荐的故障模式严酷度评分及标准表如表2所示。

表2　严酷度评分数值表

在进行定量危害性矩阵分析时，为了确保评分结果的正确性，可请熟悉产品的多名专家(或设计人员)对故障模式的严酷度进行打分，用平均值作为故障模式严酷度类别的评分值(F)，然后计算代表该故障模式点的横坐标数值。

x=F×Kx

(3)

式中：Kx为危害性矩阵图横轴(x轴)的作图比例，其单位可取mm/min。

3.2定量分析算法研究

依据定量危害性矩阵分析的原理和方法，进行定量危害性矩阵分析的算法研究。定量危害性矩阵分析算法的推导过程如下：

首先推导危害性矩阵图上的点在对角线垂足点坐标的计算公式。

设：在危害性矩阵图上有点M(x1，y1)，危害性矩阵图对角线0P的斜率为k，过点M做对角线0P的垂线，垂足为N(x2，y2)，如图2所示。

图2　定量危害性矩阵分析的解析图

从图2可知，线段0N的长度计算公式为

(4)

由上述推导过程可知，在定量危害性矩阵分析时，危害性矩阵图对角线的斜率为k，代表某个故障模式点的坐标为(x,y)，点(x,y)在矩阵图对角线的垂足点与原点(0,0)之间的距离Lj用式(5)进行计算。

(5)

(6)

式中：Ky为纵轴(y轴)的作图比例，其单位可取mm/危害度。

FMEA中，产品的各部件、零件会有多个故障模式，各个故障模式的严酷度类别会有不同，在进行定量危害性矩阵分析时，可采用求和的方法计算产品危害度的比较数值L(将产品的故障模式点与原点在矩阵图对角线上的投影距离Lj相加)，数值L可用式(7)计算。

(7)

4定量危害性矩阵分析实例

以某型飞机升降舵操纵分系统为例，进行故障模式、影响及危害性分析。飞机升降舵操纵分系统的功能是操纵升降舵，保证飞机的纵向机动飞行。升降舵操纵分系统的约定层次划分如图3所示，任务可靠性框图如图4所示，FMEA分析的严酷度定义如表3所示。

图3　升降舵操纵分系统的组成

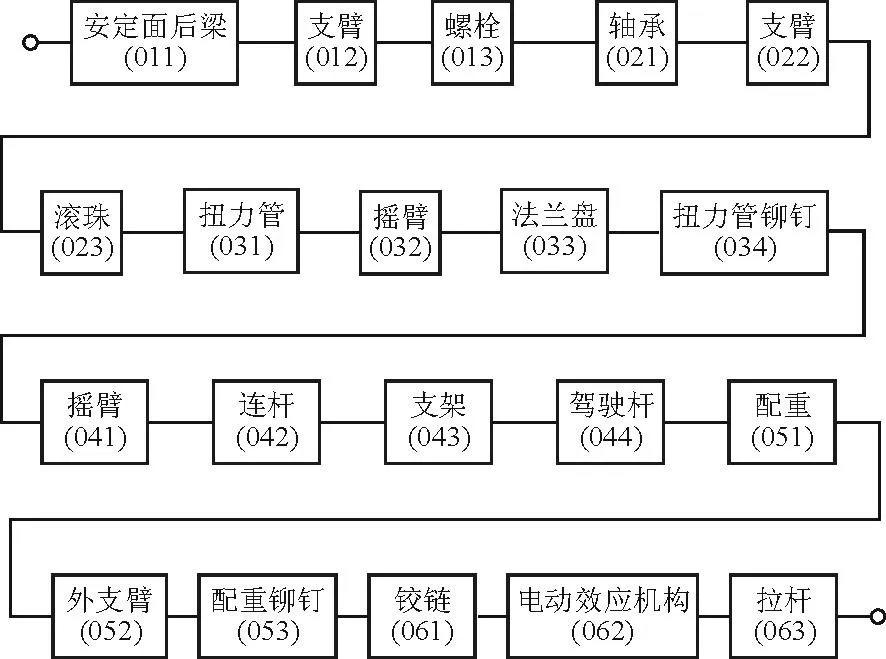
图4　某型飞机升降舵操纵分系统的任务可靠性框图

严酷度类别定 义Ⅰ类(灾难的)危及人员安全或飞机安全及重大环境损害Ⅱ类(致命的)人员损伤或飞机部分损坏及严重环境损害Ⅲ类(中等的)人员中等程度伤害或影响任务完成Ⅳ类(轻微的)无影响或影响很小,增加非计划性维护或修理

某型飞机升降舵操纵分系统的FMEA分析如表4所示，危害性分析 (CA)如表5所示，CA分析中对常用的表格进行改进，按照表2的规定进行故障模式严酷度类别的评分，定量危害性矩阵分析时的计算常数取值如下：①对角线斜率k=1；②横轴的比例Kx=5；③纵轴的比例Ky=400。表5的故障率数据λp来源于统计，可以计算各个故障模式的Lj值，进而计算产品的L值。

表4　某型飞机升降舵操纵分系统FMEA表

表5　某型飞机升降舵操纵分系统CA表

根据各部件危害度的数值 ，确定某型飞机升降舵操纵分系统改进措施的先后顺序为：调整片(06)→操纵组件(04)→轴承组件(02)→扭力臂组件(03)→配重组件(05)→安定面支撑(01)。

然而，依据表5，按照传统作图方法绘制的升降舵分系统的CA矩阵图如图5所示。经计算，各部件对应的危害度排序为：调整片(06)→操纵组件(04)→轴承组件(02)→扭力臂组件(05)→安定面(03)→配重组件支撑(01)。

配重组件(05)与扭力臂组件(03)的L值非常接近，分别为91.9和92.7，用作图法，这两个值难以区分,甚至会出现本例中的顺序刚好相反。借助本文中的计算方法，则可以很容易地进行精确排序。

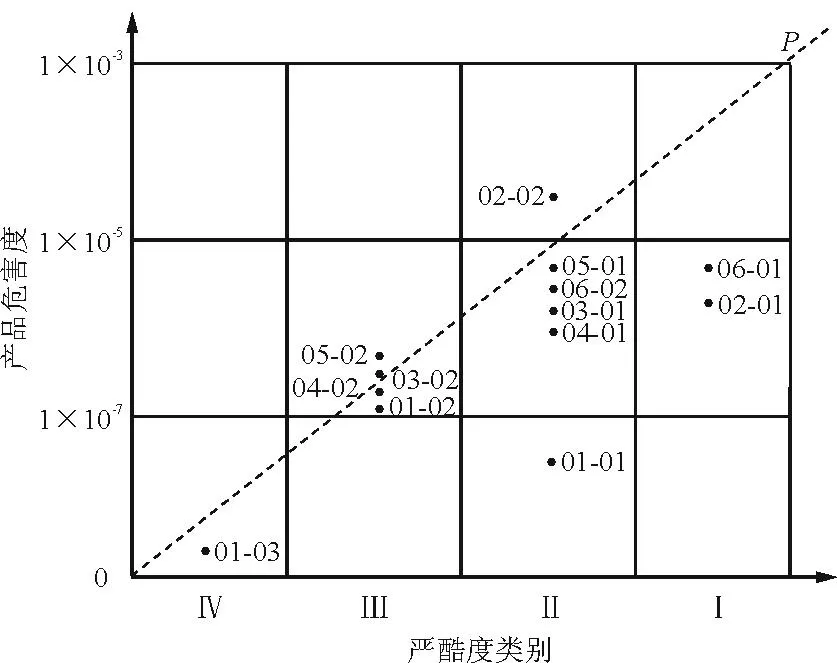
图5　传统方法的升降舵分系统CA矩阵图

5结论

(1) 对目前的FMECA中定量危害性矩阵分析方法进行了改进，将每个等级的严酷度划分为5个层次，并用显性直观的数值进行了度量。

(2) 本文的定量危害性矩阵分析的计算方法可以有效解决作图法中如果几个故障模式的严酷度相同时，由于作图法的误差导致难以判断危害度的大小，从而无法提出改进设计的优先顺序的问题。

(3) 本文的定量危害性矩阵分析的计算方法在工程中易操作，可以较好地解决目前标准、资料中方法所存在的精度差和效率低的问题，具有良好的工程指导意义和应用价值。

参考文献

[1] GJB/Z 1391. 故障模式、影响及危害性分析指南[S]. 北京: 总装备部军标出版发行部, 2006: 95-98.

GJB/Z 1391. Failure mode, effects and criticality analysis guide[S]. Beijing: The General Armament Department of Military Standard Publishing Department, 2006: 95-98.(in Chinese)

[2] 赵东元. 可靠性工程与应用[M]. 北京： 国防工业出版社， 2009: 141-143.

Zhao Dongyuan. Reliability engineering and application[M]. Beijing: National Defense Industry Press, 2009： 141-143.(in Chinese)

[3] John B Bowles, C Enrique Peláez. Fuzzy logic prioritization of failures in a system failure mode, effects and criticality analysis[J]. Reliability Engineering and System Safety, 1995, 50(2): 203-213.

[4] 崔文彬， 吴桂涛， 孙培廷, 等. 基于FMEA和模糊综合评判的船舶安全评估[J]. 哈尔滨工程大学学报， 2007， 28(3)： 264-267,276.

Cui Wenbin, Wu Guitao, Sun Peiting, et al. Ship safety assessment based on FMEA and fuzzy comprehensive evaluation methods[J]. Journal of Harbin Engineering University, 2007， 28(3)： 264-267,276.(in Chinese)

[5] 刘娜, 梁国栋, 王刘芳， 等. 电力变压器故障模式的分析及危害评估[J]. 高电压技术, 2003, 29(2)： 3-8.

Liu Na, Liang Guodong, Wang Liufang, et al. Failure mode effect and criticality analysis for condition maintenance of power transformer[J]. High Voltage Engineering， 2003, 29(2): 3-8.(in Chinese)

[6] 张大钢, 刘雁潮, 韩静. 故障模式影响及危害性分析(FMECA)技术标准发展和应用研究[J]. 质量与可靠性, 2013, 165(3): 48-51.

Zhang Dagang, Liu Yanchao, Han Jing. Failure mode effects and criticality analysis(FMECA) technology standard development and application research[J]. Quality and Reliability, 2013, 165(3): 48-51.(in Chinese)

[7] Stamatis D H. Failure mode and effect analysis: FMEA from theory to execution[M]. USA： ASQ Quality Press, 1995.

[8] Li Jun, Xu Huibin. Reliability analysis of aircraft equipment based on FMECA[J]. Physics Procedia, 2012, 25: 1816-1822.

[9] 康锐, 石荣德. FMECA技术及其应用[M]. 北京： 国防工业出版社, 2006: 35-40.

Kang Rui, Shi Rongde. FMECA technology and its application[M]. Beijing: National Defense Industry Press, 2006: 35-40.(in Chinese)

[10] 火建卫. 危害性矩阵分析中故障模式影响概率的确定方法[J]. 航空工程进展， 2015, 6(2): 229-231.

Huo Jianwei. Determination method of failure effect probability in criticality matrix analysis[J]. Advances in Aeronautical Science and Engineering, 2015, 6(2)： 229-231.(in Chinese)

王锦妮(1982-)，女，硕士，工程师。主要研究方向：飞机可靠性工程。

火建卫(1974-)，男，高级工程师。主要研究方向：可靠性设计、分析等。

(编辑：赵毓梅)

Research on Quantitative Criticality Matrix Analysis Method

Wang Jinni，Huo Jianwei

(The First Aircraft Institute, Aviation Industry Corporation of China, Xi’an 710089, China)

Abstract:In the criticality matrix, the horizontal axis is severity level and the vertical axis is criticality value of the failure mode or product. However, the failure modes can not be accurately identified while they have the same severity level. At the same time, that will lead to criticality with deviation. In addition, the efficiency of graphic method is low. A new modified calculation method of quantitative analysis of criticality matrix based on the current method is improved. An elevator sub-system is demonstrated as an example. Results show that quantitative value of failure mode or product criticality can be obtained easily, which is the basis for supporting improvement decisions.

Key words:failure mode, effect and criticality analysis; criticality matrix; criticality

作者简介：

中图分类号：TH114.3

文献标识码：A

DOI：10.16615/j.cnki.1674-8190.2016.01.010

文章编号:1674-8190(2016)01-070-08

通信作者：王锦妮,wangjinni0155362@163.com

收稿日期：2015-11-19；修回日期：2016-01-29