雷达散射截面积研究

李京娓

（四川大学计算机学院，成都 610065）

雷达散射截面积研究

李京娓

（四川大学计算机学院，成都 610065）

目标的雷达散射截面积对雷达工作性能的发挥影响很大。介绍雷达作用距离与目标雷达散射截面积的关系以及缩减目标雷达散射截面积的一些技术手段，此外还介绍一些简单和复杂目标的雷达散射截面积特性，并进行实验仿真。

雷达散射截面；雷达作用距离；RCS缩减

0 引言

雷达的基本任务是探测感兴趣的目标，测定有关目标的距离、方问、速度等状态参数。雷达信号照射到目标上时，一般会朝各个方向折射或散射。这些散射波中一部分与雷达接收天线具有相同极化，而另一部分具有不同极化，雷达接收天线不会对其做出响应。目标的雷达散射截面积（Radar Cross Section，RCS）就由与接收天线具有相同极化的后向散射能量强度来定义。雷达目标通过应用隐身技术可以大大降低自身的雷达散射截面积，影响雷达性能的发挥。即便没有应用隐身技术，目标在运动过程中，由于姿态变化或背景因素的影响，其雷达散射截面也会随其相对雷达入射波的姿态角变化而变化，因此雷达的探测距离也会不断受到缩减或放大，从而对目标追踪的性能产生影响。为了维护雷达工作的性能，对目标的RCS特性进行研究就十分必要。

目标的雷达散射截面是表征雷达目标对照射电磁波散射能力的一个物理量，是描述雷达目标信息最重要、最基本的一个参数。

1 雷达作用距离

雷达最大作用距离Rmax示如下：

其中:Pt为发射功率；G为天线增益；λ为雷达工作波长；σ为目标的雷达散射截面；n为脉冲数；Ei（n）是整合效率；k=1.38×10-23J/K为波尔兹曼常数；T0=290°为标准温度；Bn为接收方的带宽；Fn为噪声因数；S/N为单个脉冲的信噪比。

由公式可知，雷达的探测距离Rmax的四次方与目标的散射截面积σ成正比。所以目标RCS的缩减将会缩短雷达作用距离，影响雷达性能的发挥。

2 RCS缩减技术

目前已有各种有效的技术手段能够减少目标的雷达散射截面积，例如正在迅猛发展的隐身技术。隐身技术即低可探测技术，通过利用各种不同的技术手段改变目标的可探测性信息特征，最大程度降低目标被探测系统发现的概率。进行科学的外形设计或使用雷达吸收材料制造目标或覆盖目标表面，能大大降低目标的雷达散射截面积，这也是隐身技术的一个热门研究领域。

外形设计是减小雷达散射截面积的主要方式。对于外形方面的设计，其主要是高频散射机理，通过改变目标的几何外形达到使电磁波不返回发射源的目的。目前，外形设计主要基于融合式设计思想与平面设计思想两种设计理念。

使用雷达吸收材料是另一种有效实现RCS缩减的方法。雷达吸收材料能够吸收或衰减入射波，从而实现没有或只有极少的电磁反射波被反射回雷达。通过使用雷达吸收材料覆盖目标表面形成反雷达涂层或使用能吸收雷达回波的复合材料制作目标，都能有效缩减目标RCS。反雷达涂层根据对电磁波吸收原理的不同，可以分为吸收型涂层、干涉型涂层、谐振型涂层和放射性同位素涂层四类。

此外还可以使用无源对消和有源对消技术实现目标雷达散射截面积的缩减。无源对消技术又称自适应阻抗加载技术。一般通过精密加工，在目标表面形成孔洞或缝隙等，在不影响目标启动外形的前提下，改变目标表面的电流分布，被动地产生与雷达回波频率振幅相等，相位相反的附加波，与雷达回波相抵消。有源对消技术通过在飞行器上装备有源对消设备，对入射波进行处理，通过相消干涉减弱或消除反射波。这一方法要求飞行器上具有能够探测入射雷达波频率、入射角、波形和强度的高性能传感器等设备，并实时产生对消所需的电磁波信号，技术难度较高。

3 简单物体的雷达散射截面积

下面将介绍几个简单形状物体的雷达散射截面积特性，并对其进行仿真。

假设物体的极坐标为（ρ，θ，φ），则距离雷达为ρ的目标的RCS是关于（θ，φ）的函数。令（θs，φs）为散射波的传播方向。则目标的RCS为：

假设椭球体中心在(0，0，0)，由下式描述：

椭球体的雷达散射截面积为：

当a=b=c时，椭球体将变成球体，σ=πc2定义了球体的雷达散射截面积。

图1给出了椭球体（a，b，c）=（0.1，0.2，0.6）m时，分别取φ=0°，45°，90°时，椭球体的RCS关于视角θ的变化情况。

图1 椭球体RCS与视角的关系

考虑一个中心在原点，半径为r的圆形平板。由于圆具有对称性，所以圆板的RCS与φ无关，只与视角θ有关。

当法线入射即θ=0^°时，圆板的RCS为：

其他情况下则有：

其中，k=2π/λ，J1（α）为第一阶球贝塞尔函数在α处的计算值。

当取半径r=0.3m，入射频率为109Hz时，圆板的RCS与视角的关系如图所示：

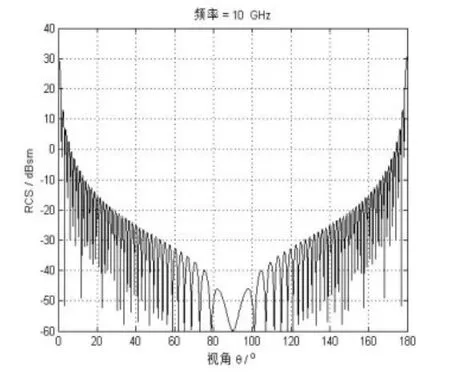
图2 圆板RCS与视角的关系

假设一个椭圆截面的圆柱体，其截面短轴半径为r1，长轴半径为r2，高为H。其法向入射的RCS为：

非法向入射RCS为：

当r1=r2时，圆柱体变为圆截面圆柱体，上式可化简为其对应的RCS公式。

当取截面半径r1=0.125，r2=0.25，圆柱体高H= 0.5m，且φ=45°、入射频率为109Hz时，圆柱体的RCS与视角的关系如图所示:

图3 圆柱体RCS与视角的关系

4 复杂目标的雷达散射截面积

复杂目标的RCS可以视为由分布在目标表面的多个散射点的贡献构成。其中，散射点通常被称为散射中心。复杂目标的RCS可以通过将组成目标的简单形状的RCS相干组合来计算。

例如，假设有一个两端为两个理想导电圆板的圆柱体。该物体是可以用很多相同的散射中心进行建模，即它是Swerling I或II型目标。

Swerling I是自由度为2的χ2分布，其概率密度函数为：

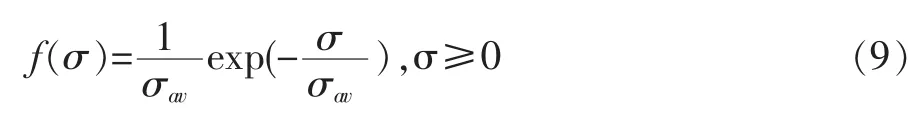
其中σav表示总的目标起伏的平均RCS。

令圆板与圆柱体截面的半径r=0.25m，圆柱体高为H=0.75m。则这个目标RCS与视角的关系如图所示:

图4 带有圆板的圆柱体RCS与视角的关系

综合图与图可以看出，在视角接近0°或180°时，目标的RCS主要由圆板决定，当视角接近90°时，目标RCS则主要由圆柱体决定。

5 结语

目标RCS的缩减将会影响雷达工作的性能，但通过对目标RCS特性的仿真可以看出，目标RCS变化与雷达视角有关，因此通过进行雷达组网，对目标区域进行多重覆盖能够增强雷达对目标的探测能力。

[1]雷达系统设计MATLAB仿真[M].电子工业出版社，2009.

[2]多源信息融合[M].清华大学出版社，2006.

[3]雷达信号处理和数据处理技术[M].电子工业出版社，2008.

[4]雷达数据处理及应用[M].电子工业出版社，2006.

[5]曾勇虎,王国玉,陈永光,等.动态雷达目标RCS的统计分析[J].电波科学学报,2007,22(4):610-613.

[6]郭琳,周德云,汪凌霄.低可探测性飞机威胁建模及航迹规划仿真研究[J].计算机仿真,2009(2):89-92.

[7]David C J.Radar and Laser Cross Section Engineering[J]，1995.

[8]曾勇虎,王国玉,陈永光,等.基于χ~2分布的目标RCS起伏特性分析[J].雷达科学与技术，2007(2):115-117.

Research on Radar Cross Section

LI Jing-wei

（College of Computer Science,Sichuan University，Chengdu 610065）

Radar cross section reduction has a huge impact on the performance of radar.Describes the relationship between RCS and radar range, and introduces some techniques for RCS reduction.It also analyzes characteristics of some simple and complex targets,and does the sim-ulation.

Radar Cross Section;Radar Range;RCS Reduction

1007-1423（2016）08-0021-04

10.3969/j.issn.1007-1423.2016.08.004

李京娓（1990-），女，山东烟台人，硕士研究生，研究方向为信息处理技术

2016-01-08

2016-03-08