大数据存储系统中负载均衡的数据迁移算法

李甜甜　王智　宋杰

摘要：认为在大数据时代，数据迁移已成为以数据为中心的挖掘分析操作的基础环节。通过对大数据存储系统中的数据迁移进行需求分析，首先提出了数据迁移模型，并分析了影响迁移性能的因素；然后基于上述模型，从作业层面提出一种负载均衡的数据迁移算法。该算法能够规避数据访问热点，提高数据迁移效率。

关键词：大数据；数据迁移；负载均衡

Abstract：In the big data era， data migration has become the basis for data centric mining analysis. In this paper， we analyze the requirements of data migration in big data storage systems and propose the corresponding migration model. We then analyze the factors affecting the migration performance. Then， using our proposed model， we design a load balanced migration algorithm from the aspect of job level， which can efficiently improve migration performance through avoiding data retrieving hotspots.

Key words：big data； data migration； load balance

随着云计算、物联网等的发展，各行业产生的数据爆炸性增长，人类已经进入大数据时代。互联网数据中心（IDC）曾在2012年的报告中指出：全球数据量每两年翻一番，至2020年将增至40 ZB[1]。大数据时代，能否从海量数据中快速获取知识来指导业务发展很大程度上决定了企业的竞争力，如何将企业各业务沉淀的数据进行全面汇总并快速返回分析结果是大数据分析亟待解决的问题。

海量数据分析往往依赖于分布式环境，然而由于业务数据类型各异，数据迁移汇总将是首要任务。能否高效、稳定地将源数据迁移到目标存储系统很大程度上决定了数据的分析效率，因此一个高效的数据迁移方法亟待发现。现有迁移技术按照应用对象不同大致可分为两类：面向虚拟机和面向存储。面向虚拟机[2-4]主要解决整个虚拟系统在不同物理环境之间的迁移问题，是整个逻辑系统或计算容器的迁移，它更多关注于实时（服务不间断）和无缝（迁移之后切换对用户透明）两个特性，与文中关注的分布式存储系统间的数据迁移不同。面向存储主要解决数据在存储系统之间或同一存储系统的不同实例之间的迁移问题，系统之间的迁移重点考虑数据的存储格式、传输路径、网络状况等因素[5-8]，实例之间的迁移重点考虑存储系统的存储形式、接口性能等一系列因素（如数据库[9-10] 、VxVM[11]、独立冗余磁盘阵列[12-13]（RAID）、云数据库[14-17]）。

文中我们研究分布式系统间的数据迁移方法，属于面向存储的数据迁移，主要关注数据的迁移性能。虽然也有类似文献同样关注于迁移性能，但大部分文献仅考虑了集群单方面的均衡，而忽略了集群间迁移作业的负载均衡性。文中我们首先结合现有需求给出数据迁移的抽象模型并分析影响迁移性能的因素；其次，基于上述模型从作业层面提出一种负载均衡的数据迁移算法；最后，通过大量实验模拟分析了该算法的均衡效果。

1 数据迁移模型

我们将数据源构成的集合记作DS={D1， D2，…， DM}，其中M代表数据源的个数，|Di|为数据源的规模；将迁移作业构成的集合记作JS={J1， J2，…， JN}，其中N代表迁移作业的个数；将每个迁移作业需要访问的数据源构成的集合记作DSj={D1j， D2j，…， DMjj}，其中Mj代表Jj需要访问的数据源个数，DSj?DS，迁移作业的规模|Jj|=∑|Dij|；将Jj从Di拉取数据的迁移任务记作P（Di， Jj），所用时间记为Tij。

迁移策略好坏最直观的衡量方式是性能，而时间是性能的最好表征，我们首先给出迁移性能的评估函数，见式（1）。其中，CJS是包含所有串行执行的作业集合中执行最慢的那些迁移作业，CDSj是Jj中包含最后结束的P（Di， Jj）的、串行运行的数据集集合，Tj表示Jj的运行时间。

从性能评估函数中可以看出：影响迁移性能的因素有CJS、CDSj和Tij，而并发度和负载均衡又是影响这三者的因素。迁移并发度越高，|CJS|和|CDS|越小，同时迁移的数据量就越多，Tij越短；数据迁移的负载越均衡，任务相互等待的时间越短，从而降低迁移作业的运行时间。

2 负载均衡策略

基于前面给出的数据迁移模型以及对性能影响因素的分析，我们设计了如图1所示的数据迁移系统，包括数据源层、作业调度层以及迁移目标层。

数据源层将不同类型的数据源水平扩展成分布式数据源；作业调度层使用MapReduce框架作为分布式程序的基础，使用YARM精确控制数据迁移使用的资源；迁移目标层使用分布式文件存储系统将目标集群虚拟为一个整体存储系统。

从上述架构中可以看出，提高迁移效率可从两方面着手：在数据源层和迁移目标层内部进行数据移动以充分利用闲置资源，从数据角度避免访问热点；在作业调度层设计实现负载均衡的迁移策略，从作业角度避免对同一块数据的热点访问。对于前者，一种称作间接迁移[18]的技术可用来实现集群内部的负载均衡，这种技术已被证明在闲置资源较多的环境中能够有效提高性能。此外，数据源层和迁移目标层的优化还可通过Sharding技术[19-20]直接保证数据的均衡分布，为高效率的数据迁移提供保证。因此，文章中我们着重研究第2种方法，通过合理调度作业尽可能错开访问同一数据源任务的执行时间。

2.1 问题定义

基于第1节给出的迁移模型，本节对迁移任务层的负载均衡问题进行形式化描述。

对给定的JS和DS，矩阵A=[aij]M×N描述Di和Jj的对应关系，矩阵B=[bjk]N×C描述Jj和Pk的对应关系，计算方法见式（2）和（3）；定义Pk的热度hk为Pk中作业运行时需要访问的所有Di中的热度最大值，Di的热度hik计算见式（4）。负载均衡的目标为寻找JS上的一个划分P_JS={Pk}并且使其满足以下约束条件：[?k∈{1，2，…，C}， Jj∈Pk|Jj|≤Ω]，且[1Chk]最小，其中Ω为目标集群的容量。

然而通过进一步分析我们发现：保证P_JS的热度总和最小并不能等价保证执行时间最短。这是因为热点访问会带来明显的性能下降。执行时间T与访问并发数b之间具有以下关联特征：T随b的增大而增大；T增长的速度随b的增大而增大。那么，必然存在一个临界点b0，使得当b>b0时并发执行的总时间大于串行执行b次的总时间，也即T>b×T0，其中T0为b=1时的执行时间。根据本文研究对象的特点，数据源的吞吐量是被严格限制的，又由于迁移作业的容器分配了足够的资源，因此b0≤1，这一结论在实际业务环境中得到了验证。

因此，P_JS还需满足以下条件：Pk包含的任意一个Jj涉及的Di的热度为1。由此可得hk=1且P_JS的热度总和[1Chk]=C。此外，鉴于迁移任务是高度并行的，且数据源又通过已有技术保证是均衡分布的，设单个迁移作业的执行时间为T0，则迁移作业的执行总时间T=C×T0，其中C=|P_JS|。至此，优化目标最终等价转换为寻找JS的一个包含元素个数最小的划分P_JS，该划分满足以下约束条件：

P_JS的最优解获取问题（记为Q0）可以归约到一个经典的NP完全（NPC）问题（均分问题），也即该问题至少是一个NP-hard问题，无法在可接受的时间范围内求解，因此文章提出Astraea近似求解算法。

2.2 近似求解

Q0的最优解需要满足式（5）中的3个条件，近似求解算法Astraea则满足了前2个条件，放宽了条件③的约束。为了量化解的近似性，文章基于数据源的访问热度与运行时间之间的关联关系给出一个近似评价函数Approxi（P_JS），见式（6）。

其中，hik为Pk中作业涉及到的Di的访问热度，hk为Pk的热度。这里，之所以选择（e-1）作为时间随热度的增速是因为它比线性增长快（与事实相符）又不至于过快而影响到解的准确性。

通过对问题Q0的解空间进行分析，发现该问题并不适合采用绝大多数传统的启发式优化算法求解，因此我们提出了Astraea近似求解算法，它运用了贪婪算法的思想，利用每一步Set Packing结果的评价值对结果集进行过滤，并使用一个树形结构对每一次Set Packing的结果进行记录，不断迭代直至算法结束，再从树中取出最优结果。

Astraea将Q0看成C次Set Packing问题，每次求得矩阵B的一列。实际运行环境中，大部分情况下|DS|比较大，但|JS|比较小，因此我们采用简单的蛮力算法解决Set Packing问题。

运行过程中，Astraea构造一个B的解空间搜索树，并对树中每个节点进行搜索。节点可以找到其父节点和子节点集合，通过序列号记录其所在层级（Pk的下标），保存第k次Set Packing得到的Pk（记作node.p，即node.k和node.p构成了Pk），记录其是否为最终节点及其评分。当前节点到根节点的路径上的所有p构成了当前解X。

Astraea的求解过程就是构造“B的解空间搜索树”的迭代过程，包含以下7步：

（1）对于任意叶子节点，根据当前节点到根节点上的所有p，构造当前调度计划X；

（2）根据X和node.p判断是否每个作业都被分配，若是则标明节点结束；否则，进入下一步；

（3）遍历所有可能的Pk，并结合X判断其是否满足条件②，保留满足条件的Pk，记为List_P。其中，Pk遍历过程的复杂度已被充分降低，后文会详细解释，条件①也在这里满足；

（4）按公式（7）计算Pk评分，Pk的热度越低越好，包含的作业个数越多越好；

（5）采用加权贪婪策略，保留前[γ]×size（List_P）个Score最大的Pk，其中[γ]是过滤参数；

（6）将剩余的Pk构造成新节点添加到当前节点的子节点中；

（7）返回第（1）步，对所有子节点进行迭代。

迭代过程结束时，Astraea得到一棵B的解空间搜索树，其叶子节点全为结束状态。这时，任意叶子节点通往根节点的路径上的Pk都可以构造一个完整的调度计划X。Astraea对所有X进行评估，近似度最高的X就是所求解。

Astraea的输入为A=[aij]M×N、可行解的过滤比例[γ]以及目标集群能容纳的任务数量[?]；输出为最优的近似解X。第（3）步的Pk遍历过程，是指在当前调度计划X的基础上，遍历下一个批次的作业集合Pk所有可能情况的过程。构造List_P实际上就是构造Pk所有可能的取值，并排除不满足条件的取值。一方面，条件①要求已分配的作业不能再次分配，因此Pk可以填入1的位置组成的集合可以通过对当前调度计划X的分析得到；另一方面，Pk中1的总数就是本次调度的作业数量。由于资源限制，每次最多处理[?]个数据集，所以Astraea可以得到当前调度计划X下最少还需要运行min个批次的作业。min个Pk中至少有一个包含的作业个数≤|NS_JS|/min，其中NS_JS为当前调度计划X下未被分配的作业集合。因为B各个列的顺序与最终运行时间无关，Astraea可以将当前的作业批次包含的作业数量的上限设置为|NS_JS|/min。

3 实验验证

针对第2节提出的Astraea近似求解算法，本节设计大量实验进行验证分析。

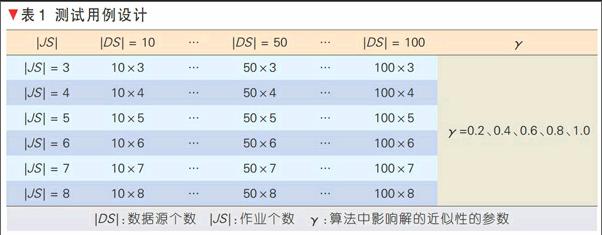
测试用例设计如表1所示，包含3个变量：作业个数|JS|、数据源个数|DS|以及算法中影响解的近似性的参数γ。其中，|JS|取值为3、4、…、 8；|DS|取值为10、 20、…、100；γ取值为0.2、0.4、0.6、0.8和1。|JS|、|DS|和γ均能够影响Astraea所求解的近似性以及算法性能，我们通过控制它们的变化来分析算法的有效性。

3.1 3个因素对解的近似性的影响

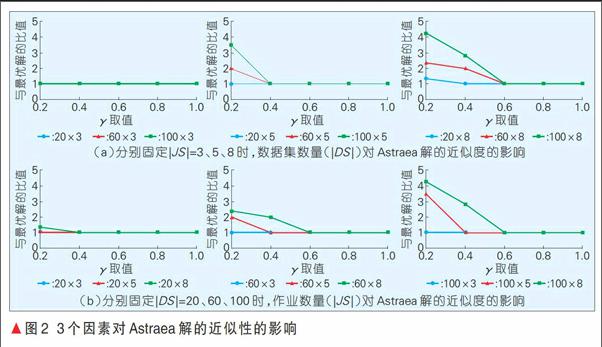
本实验主要分析|JS|、|DS|和γ对Astraea所求解的近似性的影响。当γ=1时，需对整个解空间进行遍历，此时Astraea所求解即是最优解。文中我们采用近似解与最优解执行时间之间的比值来衡量解的近似度，该比值越小越近似。此外，鉴于实验数量较多，仅选取具有代表性的几组进行展示。

图2分别展示了5组γ设置下， |DS|和|JS|对Astraea所求解的近似性的影响。在图2（a），分别固定|JS|的值为3、5和8，研究|DS|取值为20、60和100时对解的近似性的影响。从图中可以看出：当|JS|较小时（取值为3），无论|DS|取值多少，Astraea获取的解都是最优解（近似度为1）；当|JS|取值为5时，解的近似程度随着|DS|的增大而变小，但最多都在γ=0.4的时候取得最优解；当|JS|较大时（取值为8），解的近似程度也随着|DS|的增大而变小，但最多都在γ=0.6的时候取得最优解。在图2（b），分别固定|DS|的值为20、60和100，研究|JS|取值为3、5和8时对解的近似性的影响。从图中可以看出：当|DS|较小时（取值为20），解的近似程度随着|JS|的增大而变小，但最多都在γ=0.4的时候取得最优解；当|DS|取值为60和100时，解的近似程度也随着|JS|的增大而变小，但最多都在γ=0.6的时候取得最优解。

综上所述，Astraea算法获取的解与最优解之间的差距主要取决于|JS|、|DS|和γ3个因素，当|JS|和|DS|较大时，要获取较优的近似解就需要设置更大的γ。

3.2 3个因素对算法性能的影响

本实验主要分析|JS|、|DS|和γ对Astraea算法性能的影响。衡量性能最常用的指标是时间，因此本节选取算法在不同实验设置下的执行时间来衡量Astraea的性能。同样，仅选取具有代表性的几组进行展示。

图3分别展示了5组γ设置下，|DS|和|JS|对Astraea算法性能的影响，图中的纵坐标采取对数坐标轴。在图3（a）中，分别固定|JS|的值为3、5和8，研究|DS|取值为20、60和100时对Astraea算法性能的影响。从图中可以看出：算法的执行时间均随|DS|以及γ的增加而增大，并且|JS|越大，这种增长效果越明显。在图3（b）中，分别固定|DS|的值为20、60和100，研究|JS|取值为3、5和8时对Astraea算法性能的影响。从图中可以看出：算法的执行时间均随|JS|以及γ的增加而增大，并且|DS|越大，这种增长效果越明显。此处，γ是影响解的近似性的重要因素，当对Astraea算法求解的近似性越高时，γ的值就需要设置越大，进而执行的时间就越长。

综上所述，Astraea算法的性能主要取决于|JS|、|DS|和γ3个因素，|JS|和|DS|较大时，获取较优的近似解就需要设置更大的γ值，需要更长的执行时间。

4 结束语

大数据时代，高效地从数据中发现知识已经成为企业重要的竞争力之一，而存储系统间的数据迁移则是知识发现的一个基础环节。我们首先给出数据迁移模型并对迁移性能影响因素进行分析，接着基于迁移模型从迁移任务层面提出负载均衡的优化方法，最后通过实验验证提出的优化方法的有效性。迁移任务层的优化方法主要通过调控迁移任务的执行顺序使得包含同一数据源的作业尽可能避免在同一时间执行，尽可能避免迁移时的数据访问热点，从而提高迁移任务的并行性，改善迁移效率。作业调度的最优解获取问题可以证明是一个NP-hard问题，因此文中提出Astraea近似的求解算法来获取一个可接受范围内的问题解。

本中提出的负载均衡的数据迁移方法能够应用到很多系统中，例如淘宝商品搜索的索引数据存储处理系统，该系统的输入数据往往来自于多个存储系统，不同存储系统组成了一个拥有海量数据的数据源集群，需要该系统同步这些数据到Hadoop分布式文件系统（HDFS）、HBase等分布式存储系统。数据同步过程中，该系统一方面要保证数据的同步性能，同时还要尽可能降低对数据源系统查询性能的影响。文中提出的负载均衡的数据迁移方法能够成功地避开数据源的热点访问问题，从而实现系统的上述目标。

参考文献

[1] GANTZ J， REINSEL D. The Digital Universe in 2020： Big Data， Bigger Digital Shadows， and Biggest Growth in the Far East [EB/OL].[2012-03-22]. www.emc.com/leadership/digital-universe/index.htm

[2] AHMAD R W， GANI A， HAMID S， et al. A Survey on Virtual Machine Migration and Server Consolidation Frameworks for Cloud Data Centers[J]. Journal of Network and Computer Applications， 2015， 52： 11-25

[3] DERBEKO P， NATANZON A， EYAL A， et al. System and Method for Live Migration of a Virtual Machine with Dedicated Cache： US Patent 8，930，947[P]， 2015

[4] FORSMAN M， GLAD A， LUNDERG L， et al. Algorithms for Automated Live Migration of Virtual Machines [J]. Journal of Systems and Software， 2015， 101： 110-126

[5] LI C. Transforming Relational Database into HBase： A Case Sudy [C]// 2010 IEEE International Conference on Software Engineering and Service Sciences （ICSESS）. USA： IEEE， 2010： 683-687

[6] LIU C， FU Z， YANG Z， et al. General Research on Database Migration from RDBMS to Hbase[C]// 2015 International Symposium on Computers & Informatics. French： Atlantis Press， 2015： 124-237

[7] VUKOTIC A， FOX D， Partner J， et al. Neo4j in Action [M]. USA： Manning Publications， 2014

[8] SHIRAZI M N， KUAN H C， DOLATABADI H. Design Patterns to Enable Data Portability between Clouds Databases[J]. Computational Science and Its Applications （ICCSA）， 2012： 117-120

[9] PANT P， THAKUR S. Data Migration Across the Clouds [J]. International Journal of Soft Computing and Engineering （IJSCE）， 2013， 3（2）：14-21

[10] LONEY K. Oracle Database 10g： the Complete Reference [M]. USA： McGraw-Hill/Osborne， 2004

[11] MADELL T. Disk and File Management Tasks on HP-UX [M]. USA： Prentice-Hall， 1997

[12] ZHENG W， ZHANG G. FastScale： Accelerate RAID Scaling by Minimizing Data Migration [J]. FAST， 2011： 149-161

[13] KING A， CHIU D C. Efficient Fault-Tolerant Preservation of Data Integrity During Dynamic RAID Data Migration： US Patent 6，530，004[P]. 2003

[14] Chodorow K. MongoDB： the definitive guide [M]， 2nd Edition. USA： OReilly Media， 2013

[15] CHANG F， DEAN J， GHEMAWAT S， et al. Bigtable： A Distributed Storage System for Structured Data [J]. ACM Transactions on Computer Systems （TOCS）， 2008， 26（2）： 4

[16] GEORGE L. HBase： the Definitive Guide [M]. USA： OReilly Media， 2011

[17] ANDERSON JC， LEHNARDT J， SLATER N. CouchDB： the Definitive Guide [M]. USA： OReilly Media， 2010

[18] ANDERSON E， HALL J， HARTLINE J， et al. An Experimental Study of Data Migration Algorithms [M]. British： Springer， 2001

[19] BAGUI S， NGUYEN L T. Database Sharding： To Provide Fault Tolerance and Scalability of Big Data on the Cloud [J]. International Journal of Cloud Application Computing， 2015， 5（2）：36-52. http：//dx.doi.org/10.4018/IJCAC.2015040103

[20] LIU Y， WANG Y， JIN Y. Research on the improvement of MongoDB Auto-Sharding in Cloud Environment[C]// 2012 7th International Conference on Computer Science & Education （ICCSE）. USA： IEEE， 2012： 851-854