灌区尺度遥感蒸散发模型时间尺度提升方法研究

陈 鹤，蔡甲冰，张宝忠，白亮亮(1.中国水利水电科学研究院，流域水循环模拟与调控国家重点实验室，北京 100038；2.国家节水灌溉北京工程技术研究中心，北京 100048)

0 引 言

随着遥感技术的成熟与发展，采用遥感数据模拟灌区尺度蒸散发成为可能，但卫星遥感通常仅提供每日1～2次卫星过境时刻的瞬时数据，卫星过境重现期约为1～16日，在应用过程中还需要将受云层遮挡日期的数据剔除。因此，在计算灌区作物耗水量时，需要先将遥感模型得到的瞬时蒸散发，通过时间尺度扩展方法转化为日蒸散发量，再将不连续的日蒸散发进行尺度提升，得到全生育期的蒸散发。遥感蒸散发模拟的精度除了受到模型精度本身的影响外，更大程度上受到时间尺度提升方法精度的影响。因此一方面要优化遥感蒸散发模型时间尺度提升方法，减小从瞬时到日时间尺度提升带来的误差；另一方面要最大程度地利用获取的遥感数据，减小从日到生育期时间尺度提升带来的误差。所以，本文构建了日内代表性参数方法实现由瞬时到日的尺度提升，优化了传统遥感蒸散发模型中时间尺度扩展的步骤，避免了气象数据降尺度和遥感蒸散发升尺度造成的二次误差，该方法采用日内代表性参数直接计算日蒸散发，同时采用逐象元进行插值的方法进行从数据日到全年的时间尺度提升，最大化利用有效遥感数据，提高了估算精度。

1 材料及数据

1.1 研究区概况

本文以河套灌区解放闸灌域(106°43′～107°27′E，40°34′～41°14′N)为研究对象(图1)。灌域总土地面积约2 345 km2，其中70%以上为耕地，粮食作物以夏玉米和春小麦为主，经济作物以向日葵为主，伴有一定比例的瓜果、蔬菜。灌域地处干旱半干旱内陆地区，海拔高程在1 030～1 046 m之间，年平均降雨量151.3 mm，年均蒸发量(20 cm蒸发皿)达2 300 mm，年内平均气温9 ℃[1]。

1.2 数据来源

1.2.1遥感数据及数据预处理

本文用到的遥感数据来源于Terra和Aqua卫星上搭载的 MODIS 传感器观测的标准陆地产品，其中Terra卫星的过境时间为10∶30 左右，Aqua卫星的过境时间为13∶30 左右。MODIS传感器提供空间分辨率为250～1 000 m，时间分辨率为1～16日。以上遥感数据通过NASA数据平台下载( http:∥reverb.echo.nasa.gov/reverb/)，遥感标准陆地产品已经过辐射、大气和几何校正，通过MRT工具重投影到WGS84/UTM(北48区)坐标系统，空间分辨率重采样到250 m，并进行质量控制、数据插补及平滑[2]等预处理环节，得到最终的遥感数据集。

1.2.2气象数据

本文用到的气象数据来源于灌区内及周边的10个国家气象站，观测项目包括日降水量，日内最高、最低气温及日平均气温，日平均相对湿度，日平均风速及日照时数等。采用距离方向加权平均法对气象数据进行空间插值[3]，得到250 m空间分辨率的逐日气象数据集。

1.2.3土地利用数据

土地利用数据来源于清华大学遥感中心制作的2010年30 m分辨率土地利用图(图1)[4]，研究区域主要土地利用类型为农田(76.81%)，其次为灌木(11.52%)和草地(10.29%)，其他土地利用类型占比极低，城镇面积仅为0.86%。

图1 2010年研究区域30 m分辨率土地利用图

2 时间尺度提升方法

2.1 瞬时到日的时间尺度提升

以往遥感蒸散发模型的计算日蒸散发的流程是：①根据卫星过境时刻的遥感数据，反演瞬时地表参数；②对气象数据进行降尺度，得到卫星过境时刻的气象数据；③建立遥感蒸散发模型，计算瞬时蒸散发；④将瞬时蒸散发进行时间尺度提升计算日蒸散发。在此过程中，除去遥感模型本身的误差，对气象数据降尺度和对瞬时蒸散发进行升尺度均会带来不可避免的误差。本文提出日内代表性参数法，规避了将气象数据降尺度来计算瞬时蒸散发的过程，利用对瞬时遥感数据进行积分得到日内代表性遥感数据，通过气象站获取的日内代表性气象数据，直接计算日蒸散发。

采用日内代表性法计算日蒸散发的遥感模型有两个优点：①日蒸散发量直接由模型计算，避免了尺度扩展过程中的误差，从而提高模型模拟精度；②对模型输入气象数据的要求降低，避免了气象数据降尺度的过程，减小了计算误差。

假定地表温度在白天的变化规律符合正弦曲线，通过遥感卫星反演，得到Terra和Aqua卫星过境时刻的2次地表温度观测值，因此假定地表温度在白天的变化为一段正弦曲线：

Tt=asin(bt+c)

(1)

式中：下标t表示当地时间；a，b，c分别是正弦曲线参数，由下式计算：

a=TAqua

b=[arccos(TTerra/TAqua)]/(tAqua-TTerra)

c=π/2-tAquab

(2)

式中：tAqua和tTerra分别是Aqua和Terra卫星过境的时间；TAqua和TTerra分别是Aqua和Terra卫星过境时刻的地表温度。则日内代表性地表温度为：

(3)

式中：Ts为日内代表性地表温度；tsunrise和tsunset分别为日出及日落时刻(见表1)。

表1 研究区域日出日落时刻

由于地表反照率在日内变化幅度很小[5]，日内代表性地表反照率采用Terra和Aqua卫星过境时刻地表反照率平均值。风速、相对湿度和空气温度采用气象站观测的日平均值作为代表性参数。以日内代表性参数为模型输入，通过下节中介绍的遥感蒸散发模型，即可直接计算日蒸散发。

2.2 遥感蒸散发模型

本文采用基于能量平衡原理的SEBS(Surface Energy Balance System)模型[6]，SEBS模型区别于其他单层模型的特点在于通过引入剩余阻抗的概念来描述植被冠层和地表间热量及动量粗糙长度的差异。SEBS模型包含以下4个模块：①基于遥感空间反照率和辐射率的地表物理参数反演；②热量粗糙长度的计算；③显热通量的计算；④潜热通量的计算。与其他基于能量平衡原理的单层模型相比， SEBS 模型的优点在于每一个象元的计算都是独立的，因此即使在某天某些象元因为阴雨或云等影响缺乏遥感数据，也并不影响其他象元的计算结果，可以最大化地利用遥感数据。

SEBS模型中需要计算不同土地利用类型及下垫面的动量粗糙长度(z0m)，其中非作物的z0m取值见表2，作物的z0m根据下式计算：

(4)

X=CdLAI

式中：h为冠层高度；Cd为叶片拖曳系数，通常取值为0.2；z0s为底层粗糙长度，通常取值为0.01；LAI为叶面积指数；d为零平面位移。

计算公式如下：

d=1.1 ln(1+X1/4) (5)

2.3 日到全年的时间尺度提升

卫星遥感观测数据受天气影响较大， 在有降雨或者受云层遮挡的日子，没有可用的遥感影像，无法利用模型模拟日蒸散发，需要对数据缺失日期进行插补。

以往遥感蒸散发模型从日到全年的时间尺度提升通常以整个灌区为单位，先筛选可用的遥感影像(有效象元占整个研究区域90%～95%)，再填补可用遥感影像间的缺值日期。为最大化利用遥感数据，本文对遥感蒸散发模型从日到全年的提升以象元为单位，首先计算全年内所有日期有效遥感象元的日蒸散发，再逐象元填补该象元的缺值日期。尺度提升方法采用蒸发比插补法，假定蒸发比(潜热通量与有效能量的比值)在全年呈现连续变化的趋势，对有值日蒸发比进行插值计算无值日蒸发比，进而得到无值日蒸散发，从而实现日蒸散发的连续模拟。

图2是基于遥感数据的灌区尺度ET计算流程图。

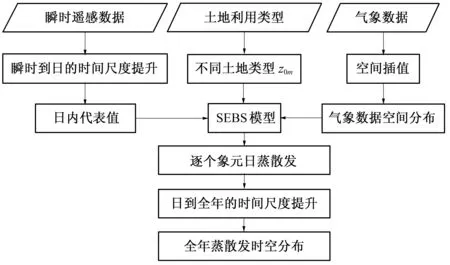
图2 计算流程图

3 结果与讨论

3.1 日蒸散发尺度提升及插补

图3为日内代表性参数法计算得到的日蒸散发，从图3中可以看出，2014年8月14日有大量象元受到云层遮挡没有可用遥感数据，8月15日整个研究区域遥感数据均可用，这代表了利用遥感数据计算蒸散发的两种情况。

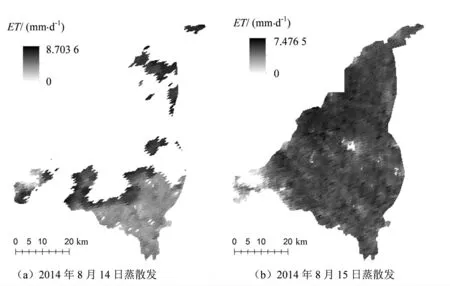
图3 遥感蒸散发模型模拟日蒸散发空间分布

以区域内第(200，200)号象元为例，进行日尺度到全年尺度插值(图4)并计算该象元每日蒸散发。对研究区域内每个象元进行时间尺度提升，得到每日连续的蒸散发空间分布，以图5中8月14日的结果为例。

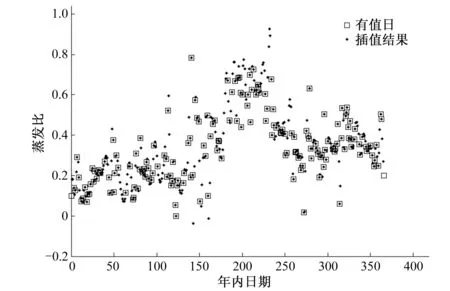
图4 日尺度到全年尺度蒸发比插值结果

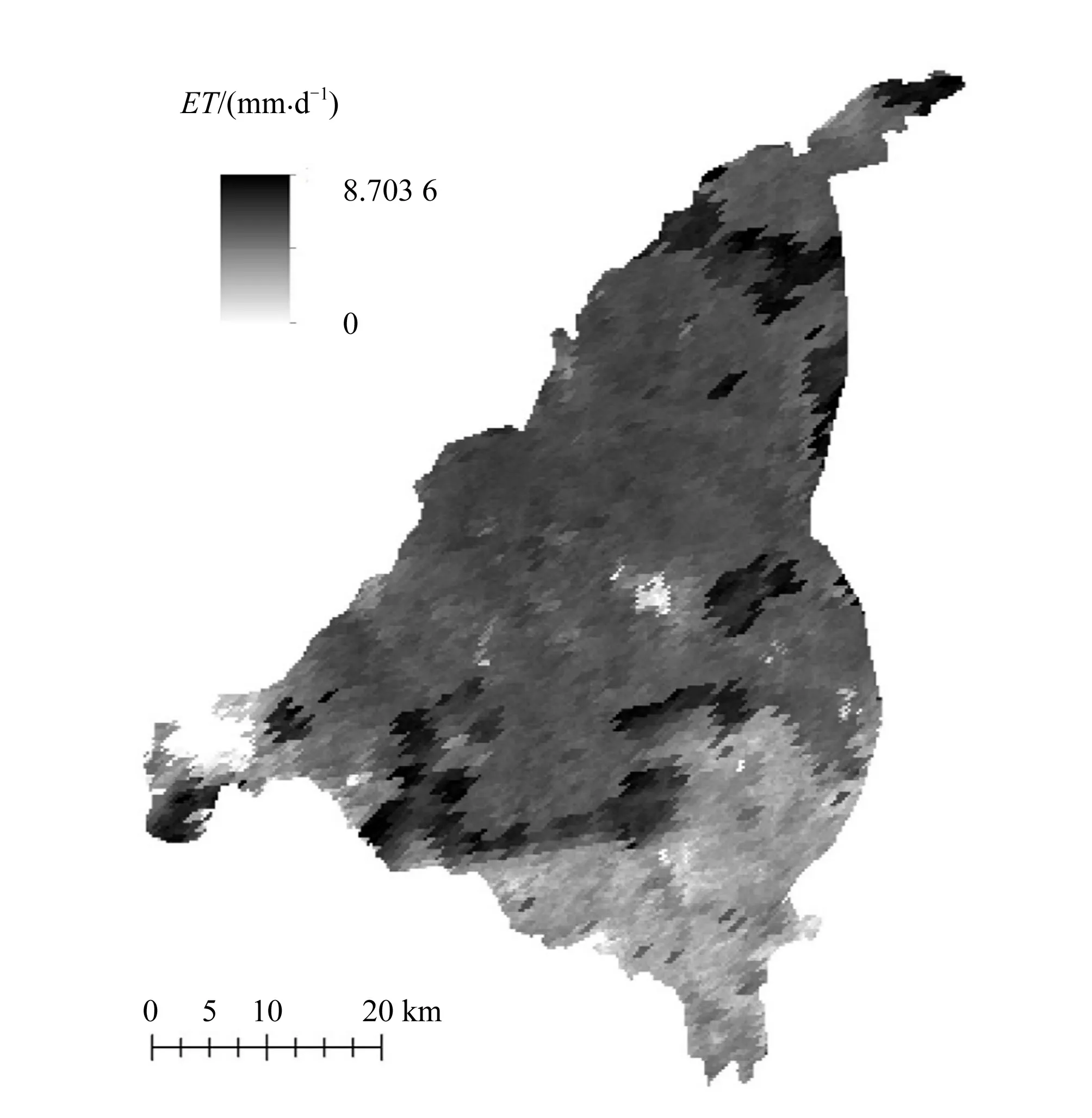
图5 数据插补后2014年8月14日蒸散发空间分布

从图中可以看出，通过插补得到的无值区的蒸散发结果要小于通过遥感模型直接计算的有值区结果，这是因为在受到云层遮挡的情况下，向下短波辐射值比较小因此有效能量较小，与实际情况是相符的。

3.2 灌区蒸散发时空变化

在对蒸散发模型进行尺度提升后，得到如图5所示的每日灌区蒸散发空间分布，进而得到全年的蒸散发空间分布(图6)。2014年解放闸灌域全年降雨量126 mm，实际蒸散发899 mm，其中作物生长季(4-9月)为650 mm，占全年蒸散发总量的72.3%。从蒸散发的空间分布情况来看，灌域北部要高于南部，尤其灌域西南角由于耕地荒漠化的原因，蒸散发量小于北部。

图6 2014年解放闸灌域实际蒸散发空间分布

3.3 讨 论

对2014年遥感数据进行分析，若采用以往常规的日尺度到年尺度提升方法，全年可利用影像(有值象元占全区域95%以上)为52幅，其中最早可用日期为3月26日，最晚可利用日期为10月8日。而利用逐象元的时间尺度提升方法，灌区内所有象元平均可利用天数为139日，最好的象元可利用天数为211日，最差的象元可利用天数也达到92日，采用逐象元提升的方法可将遥感数据利用率提高1倍以上。

4 结 语

本文探讨了利用遥感数据计算灌区蒸散发的时间尺度提升方法，分别从瞬时到日以及日到全年两个尺度进行研究。在瞬时到日尺度，采用日内代表性参数法结合SEBS模型，规避了以往传统蒸散发模型中先计算瞬时蒸散发，在进行时间尺度提升计算日蒸散发的过程。在日到全年尺度，采用逐象元进行插值的方法，最大化利用遥感数据。将SEBS模型应用于内蒙古河套灌区解放闸灌域进行一整年的连续模拟，并得到研究区域的实际蒸散发时空分布。

本文构建的遥感蒸散发模型时间尺度提升方法，相比于传统的遥感蒸散发模型，步骤简单，遥感数据利用率高，为灌区实际蒸散发模拟提供了极具操作性的参考价值。

□

[1] 茌伟伟．基于分布式水温模型的灌区用水效率评价[D]．北京：中国水利水电科学研究院，2013．

[2] Velleman P. Definition and comparison of robust nonlinear data smoothing algorithms [J]. Journal of the American Statistical Association, 1980,75(371):609-615.

[3] 杨大文，李 翀，倪广恒，等．分布式水文模型在黄河流域的应用[J]．地理学报，2004，59(1)：143-154.

[4] Gong P, Wang J, Yu L, et al. Finer resolution observation and monitoring of global land cover: first mapping results with Landsat TM and ETM+ data[J]. International Journal of Remote Sensing, 2013,34(7):2 607-2 654.

[5] Chen H, Yang D, Remote sensing based continuous estimation of regional evapotranspiration by improved SEBS model[C]∥ Land Surface Remote Sensing, eds. Entekhabi Dara, et al. Proceedings of SPIE, Vol. 8524, 852401. Kyoto, Japan, 2012.

[6] Su Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes [J]. Hydrology and Earth System Sciences, 2002,(6):85-99.