基于MODIS数据的土壤水分空间变异规律

汝博文 ，缴锡云，王耀飞，郭维华

(1.河海大学水文水资源与水利工程科学国家重点实验室，南京 210098；2.河海大学水利水电学院，南京 210098；3.河南省水利勘测设计研究有限公司，郑州 450000)

土壤水分空间变异的研究对于高效监测土壤水分动态变化、改善农业灌溉决策管理和提高农业用水效率有重要的意义。 Herbst等[1]分析德国一小尺度田块(0.29 km2)0～20 cm土层土壤水分的空间变异，并用10 m×20 m的网格在1 hm2的田块内取样，发现土壤含水率变异函数符合球状模型，其变程约为53.8 m。Brocca等[2,3]在100 m×50 m和110 m×80 m的网格中取样，分析了0～150 cm深度的土壤水分空间变异性，认为变异函数符合指数模型，变异系数分别为11%～20%和11%～16%，其变程约为10～15 m。张淑娟等[4]在13.3 hm2的区域内用50 m×50 m的网格取样，分析冬小麦褐土0～20 cm深度内土壤水分的空间变异，发现变异函数符合球状模型，变异系数约为15.11%，变程为246.8 m。目前国内外对中小尺度区域的土壤水分空间变异性进行了大量的研究[5,6]，然而对大尺度区域土壤水分空间变异性研究却鲜有涉及，这主要是因为获取墒情的传统方法一般为手工或半自动的方法，只能获取点或者小范围的墒情信息，而对于尺度较大的研究区域，大范围的墒情采集存在着较大的难度，对于这一问题，卫星遥感技术的发展为大范围的土壤墒情采集提供了可能。遥感影像能够反映地物目标电磁辐射特性的能量分布，它能够将地表的信息特征客观、真实、连续地记录下来[7]。近年来，MODIS和TM等高分辨率数据被越来越多的应用于土壤水分信息的提取。Modis是搭载在Earth Observation System(包括Terra和Aqua)卫星上的一个重要的传感器，具有较高的时间分辨率和空间分辨率，因此本文以Modis数据为研究对象，结合实测含水率数据，运用植被供水指数法[8-11]构建土壤水分遥感模型，进而得到沧州地区整体的土壤墒情状况，并以此为基础，运用经典统计学和地统计学理论研究不同尺度下的土壤水分空间变异规律，对于提高农田墒情信息的采集效率具有重要意义。

1 研究区概况与数据来源

(1)研究区概况。本文以河北省沧州市为研究区域，地理坐标北纬37°29′～38°57′，东经115°42′～117°50′，总面积约为1.4万km2，全境年平均干燥度1.2～1.5。由于季风气候的影响，年降水量约为400～500 mm，年平均水面蒸发量1 500～1 800 mm，主要集中在夏季(七八月份)。研究区域光热资源丰富，多年平均日照时间2 318 h，太阳总辐射2 342.1 kJ/cm2，年积温大于4 300 ℃。

(2)数据来源。本文所需要的MODIS数据从http:∥ladsweb.nascom.nasa.gov/data/search.html网站下载，选用的数据为MODIS数据的2级产品：MODIS 1B数据影像产品。实测土壤含水率采集于沧县、盐山、献县、南皮、青县、河间、泊头等7个县市，土样采集时间尽量与卫星过境时间同步，每个采样点分两层取土，采样深度分别为0～20、20～40 cm。

2 研究方法

2.1 植被供水指数

植被指数(Vegetation Index)是指能够反映绿色植物分布和生长状况的特征指数[12]，植被供水指数与土壤水分状况存在着十分密切的关系，当植被供水正常时，植被指数在一定的生长期内保持在一定的范围；如遇干旱，植被供水不足，植被供水指数会因为植被生长受到抑制而降低。在计算植被指数时，常选用近红外波段和可见光波段，因为该波段对植被指数最为敏感。本文利用第1、2、31、32等波段值计算植被供水指数：

(2)

式中：VSWI是植被供水指数；NDVI是归一化植被指数；Ts是植被冠层温度，℃；ρ1、ρ2分别为MODIS第1、2波段反射率。

利用遥感得到的植被供水指数，可以通过统计分析软件SPSS，建立植被指数与实测土壤水分之间的关系模型，进而估算墒情。

2.2 墒情采集

在通过遥感得到沧州地区墒情的基础上，选取面积为4.5 km×4.5 km、18 km×18 km、56 km×56 km的区域进行墒情信息的采集。对于面积为4.5 km×4.5 km的区域，在该尺度区域内内嵌250 m×250 m的网格进行取样，取点324个。在面积为18 km×18 km的区域内内嵌1 km×1 km的网格取样，取点324个。在面积为56 km×56 km的区域内内嵌4 km×4 km的网格取样，取点196个。上述3种取样尺度分别对应小、中、大尺度。

2.3 数据处理及分析

采用ENVY软件对MODIS数据进行处理，通过SPSS 13.0软件构建植被供水指数与实测土壤含水率之间的关系模型。运用GS +7.0软件对遥感得到的研究区域内的土壤含水率进行空间变异性分析，并使用Arcgis10.0软件的地统计分析模块对研究区域内的土壤含水率进行普通克里格插值，在得到土壤含水率分布图的基础上确定研究区域内土壤水分监测点的合理取样数目，进而为确定土壤墒情监测点的合理布设提供一定的理论和基础。

3 结果分析

3.1 植被供水指数-土壤含水率模型

利用SPSS软件将地面采集到的0～20、20～40 cm深度处的土壤含水率(体积)数据与遥感数据计算得到的植被供水指数进行拟合，绘制植被供水指数(VSWI)与0～20、20～40 cm深度处的实测土壤含水率的关系散点图(见图1和图2)，并对二者进行相关分析，构建植被供水指数-土壤含水率模型，见表1和表2。在模型的构建过程中，为便于分析，将植被供水指数VSWI放大10 000倍，土壤体积含水率以百分比的形式表示。

图1 植被供水指数与0～20 cm深度处土壤含水率散点图Fig.1 Scatter of vegetation supply water index and 0～20 cm soil water content

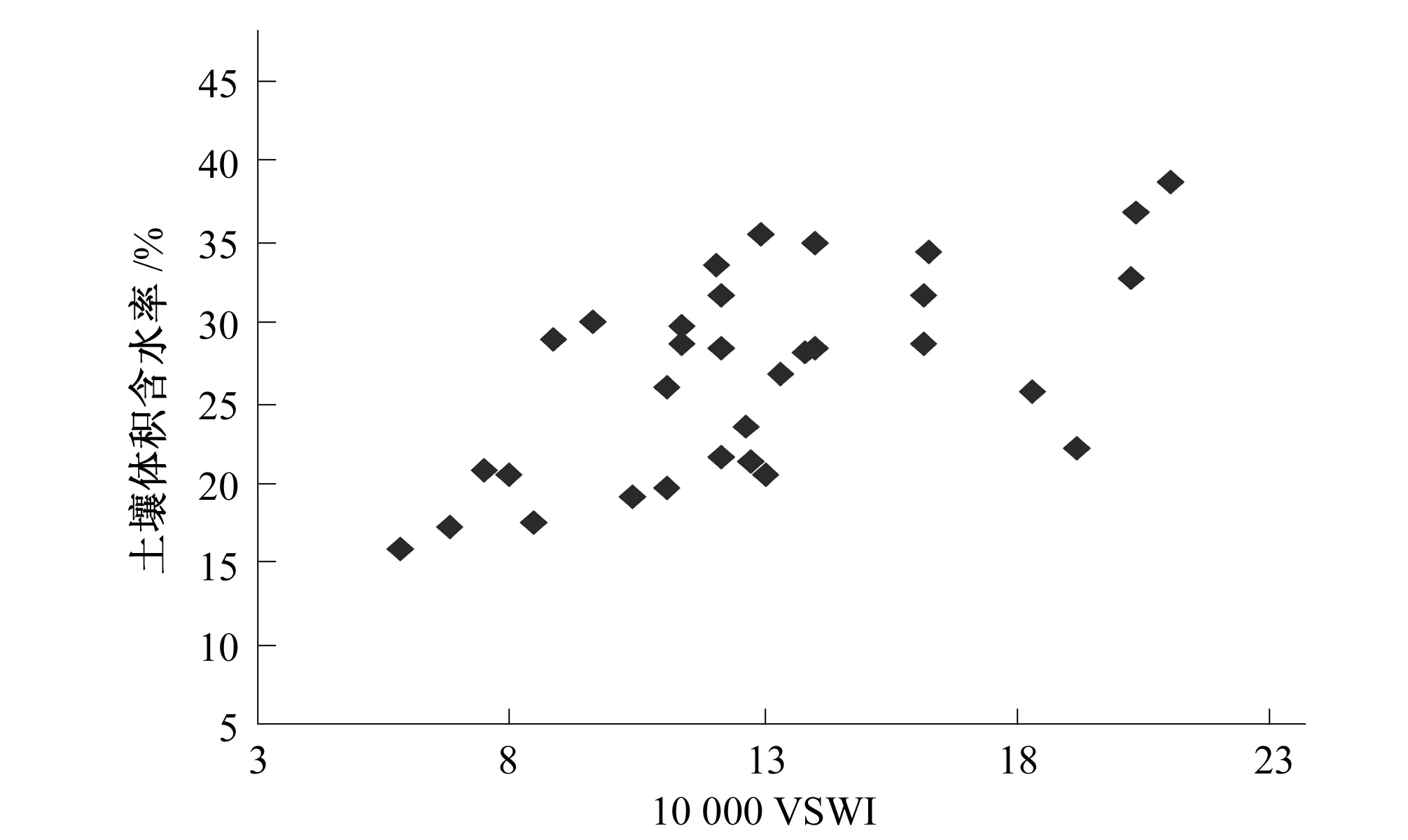
图2 植被供水指数与20～40 cm深度处土壤含水率散点图Fig.2 Scatter of vegetation supply water index and 20～40 cm soil water content

由表1、表2植被供水指数与0～20、20～40 cm深度处土壤含水率所构建的模型可知，以上各模型均通过了置信度为0.001的F检验，表现出了极显著的相关性，并且均有较高的相关系数值，其中线性模型使植被供水指数与0～20 cm深度处土壤含水率的拟合程度达到最好，相关系数R2为0.621。幂函数模型使植被供水指数与20～40 cm深度处的土壤含水率的拟合程度达到最好，相关系数R2为0.642。本研究中植被供水指数与0～20 、20～40 cm深度处的土壤含水率的相关性较为显著，与之建立的相关模型的精度较高，故可以利用植被供水指数-土壤含水率模型对0～20 、20～40 cm深度处的土壤含水率进行评估并计算得到整个研究区域0～20、20～40 cm深度处土壤含水率。在此基础上对土壤含水率进行基于专家知识的决策树分类，绘制出0～20、20～40 cm深度处土壤水分的分布状况，分别如图3和图4所示。

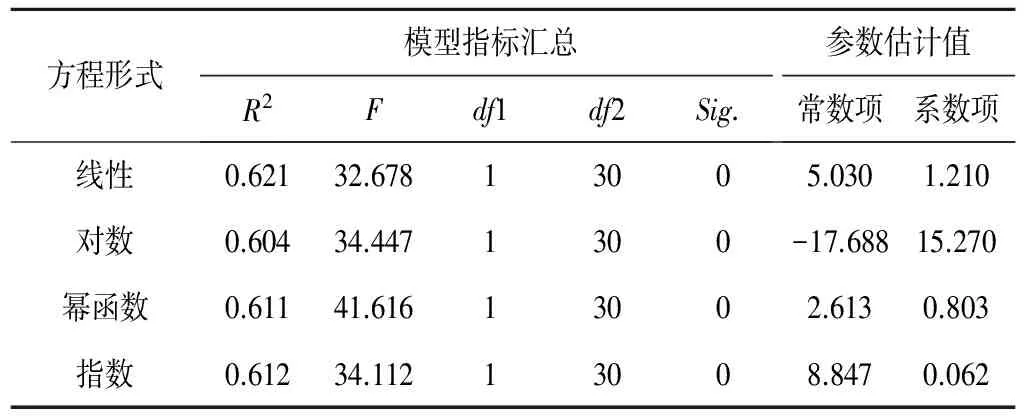
表1 植被供水指数与0～20 cm深度处土壤含水率模型拟合参数表Tab.1 The fitting parameters of vegetation supply water indexand 0～20 cm soil moisture content

表2 植被供水指数与20～40 cm深度处土壤含水率模型拟合参数表Tab.2 The fitting parameters of vegetation supply water indexand 20～40 cm soil moisture content

图3 2013年5月20日沧州市0～20 cm农田墒情分布图Fig.3 The 0～20 cm soil moisture distribution of Cangzhou on May 20,2013

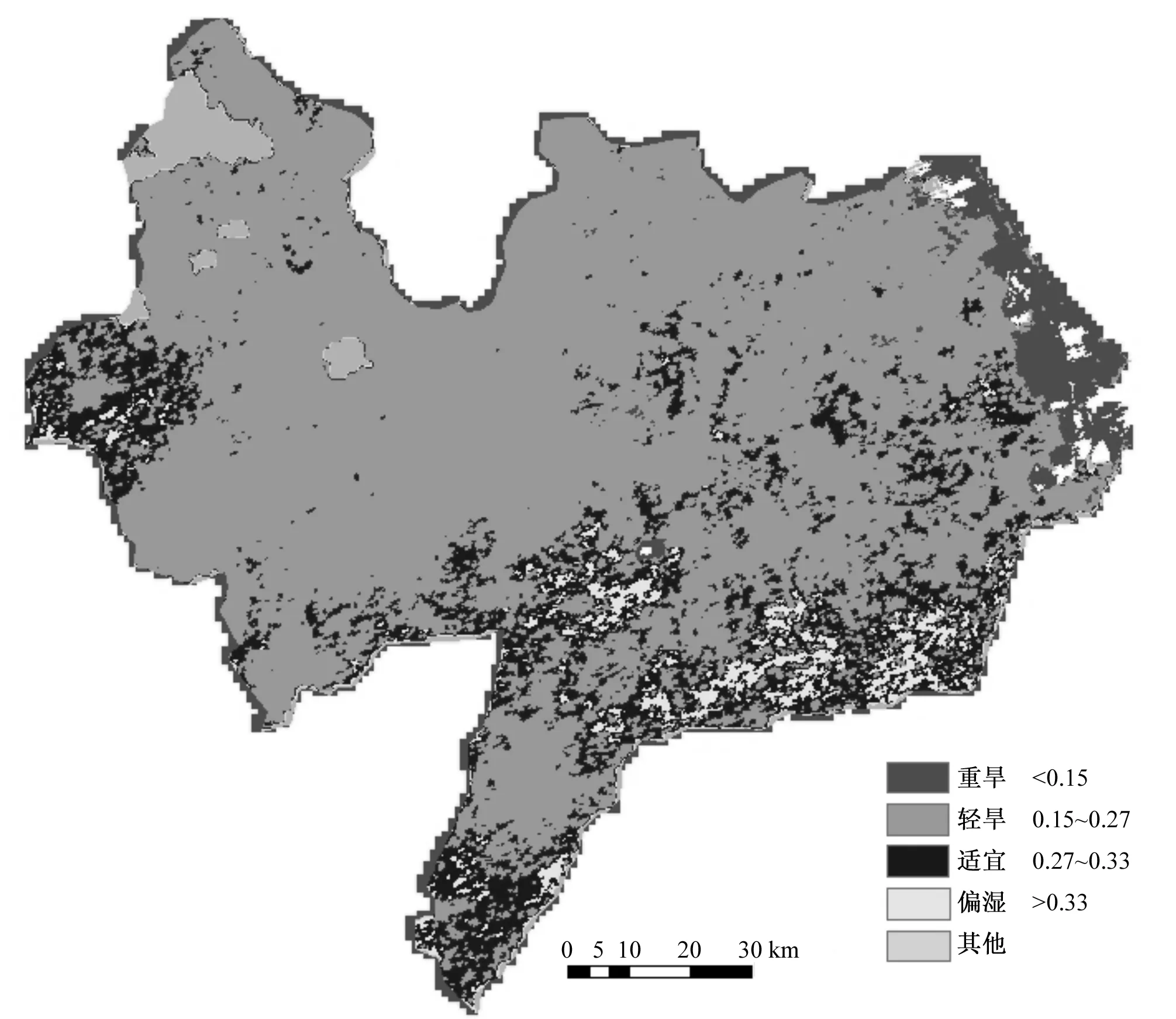
图4 2013年5月20日沧州市20～40 cm农田墒情分布图Fig.4 The 20～40 cm soil moisture distribution of Cangzhou on May 20,2013

3.2 土壤水分的统计分析

对不同尺度下0～20、20～40 cm深度处的土壤含水率进行统计分析，其土壤含水率统计特征值见表3。

土壤含水率的变异系数反映了各个区域内土壤含水率样本的离散特征。一般将变异系数小于0.1时定义为弱变异性，将变异系数大于0.1且小于1.0时定义为中等变异性，将变异系数大于1.0时定义为强变异性[13]。由表3可知不同尺度下0～20 cm深度处土壤含水率均表现为中等变异性，其中小尺度下的土壤含水率的变异系数最小，中尺度次之，大尺度变异系数最大。而对于20～40 cm深度土壤含水率，小尺度下的土壤含水率表现为弱变异性，而中尺度及大尺度的土壤含水率均表现为中等变异性，其中大尺度的变异系数最大。由此可见随着研究尺度的增大，变异系数随之增大。这主要是因为在面积较小的区域内，土壤含水率之间的相关关系较强。而随着研究尺度(研究区域面积、采样间距)的增大，土壤含水率之间的相关关系逐渐减弱，变异性逐渐增强。此外，所有尺度的土壤含水率均表现弱变异性或中等变异性，可能是因为此时整个沧州地区土壤含水率处于相对较低的水平，导致其变异性减弱。

表3 不同尺度土壤含水率统计特征值Tab.3 Statistical characteristics of soil moisturecontent at different grid scale

3.3 土壤水分的空间变异性分析

土壤水分的空间变异性不单服从经典统计学规律，同时也具有一定空间结构性特征，其变异函数会随着研究尺度的变化而变化。本文在通过遥感信息反演沧州地区墒情信息的基础上，研究不同尺度下土壤水分在二维平面上的空间变异结构特性。利用GS+7.0软件分别对不同尺度0～20、20～40 cm的土壤含水率数据进行统计分析，计算其半方差函数值并得到半方差模型参数(见表4)。一般认为块金值(C0)表示由随机因素引发的空间变异程度，基台值(C0+C)则表示变量的最大变异程度。二者的比值[C0/(C0+C)]表示随机部分引起的空间变异占系统总变异的比值。比值越高，由随机部分引起的空间变异程度越大；比值越小，则说明由随机部分引起的空间变异程度越小。当块金基台比小于25%时，表明空间变量之间具有强烈的空间相关性；当块金基台比大于25%且小于75%时，表明变量之间具有中等程度的空间相关性；当块金基台比大于75%时，则表明变量之间的空间相关性较弱，空间变异主要由随机因素引起[14]。

表4 不同研究尺度土壤含水率的半方差函数理论模型及其相关参数Tab.4 Variation model for soil moisture content andits relative parameters at different grid scale

由表4可知，3种不同尺度下0～20、20～40 cm深度处土壤含水率的半方差函数最佳理论模型均为球形模型，其决定系数大部分接近于1，说明球状模型能够很好地反映土壤水分的空间结构特征。

3种尺度下0～20 cm深度处的块金值大于20～40 cm深度处的块金值，说明土壤上层水分的空间变异更容易受随机因素的影响。小尺度下0～20、20～40 cm深度处的土壤含水率的块金基台比均小于0.25，表现为强烈的空间相关性，说明该尺度各层土壤水分的空间变异主要由结构因素引起。中尺度及大尺度下0～20、20～40 cm深度处的土壤含水率的块金基台比介于0.25～0.75之间，表现为中等的空间相关性，表明各深度土壤水分的空间变异由随机因素和结构因素共同作用。研究尺度不同，块金基台比表现出一定的差异。随着研究尺度的增大，块金基台比逐渐增大，空间相关性逐渐减弱，由随机因素引起的空间变异逐渐增强，由结构因素引起的空间变异逐渐减弱，这可能是因为研究尺度(研究区域面积、采样间距)的增大，导致土壤水分的细小结构被掩盖，结构性变异减小，随机性变异变大。变程表示样本点之间达到最大变异程度的空间距离[15]，样本之间的距离在变程范围内，则样本之间存在空间相关性，若样本之间的距离大于变程，则样本之间的空间相关性消失。从表4中可以看出，3种不同尺度下0～20 cm深度处土壤含水率的变程在2 488～11 806 m，20～40 cm深度处土壤含水率的变程在2 233～11 296 m，随着土层深度的增加，变程值减小，随着研究尺度的增大，各层土壤水分的变程值逐渐增加。

3.4 基于普通克里金插值法的土壤水分空间分布图

为更加直观的反映研究区域土壤水分的空间分布，使用ArcGIS10.0软件的地统计分析模块对各区域的土壤含水率进行普通克里格插值，绘制出各区域0～20、20～40 cm深度处土壤水分的空间分布图，见图5。

以小尺度不同深度土壤含水率为例，可以看出随着土层深度的增加，土壤含水率趋于变大，各层土壤含水率分布大体一致，表现为东北高而西南低。0～20 cm土壤含水率的空间变异性大于20～40 cm土壤含水率的空间变异性。随着研究尺度的增大，土壤含水率的空间变异性逐渐增强，但部分区域插值后的土壤水分连续性反而增大，土壤水分分布更加均匀，这主要是因为随着采样间距的增大，插值所用的有效变程也随之增大，从而掩盖了土壤水分分布的一些细微结构，使得插值后的土壤水分连续性增大，水分分布更加均匀。

3.5 土壤水分监测点的合理布设数目

确定合理的土壤水分监测点数目，即要求工作量最小，又要满足一定的精度要求。本文依据经典统计学理论，采用如下公式确定显著性水平为α时土壤水分监测点的合理采样数目。

(3)

式中：tα,f为自由度为f时的T分布的特征值，可以从统计表中查到；S为样本的标准方差；d为采样误差即样本总量均值与测量值均值之间允许的偏离值，一般取d=kμ，其中k取5%、10%、15%、20%等。

依据上述公式，分别选取置信度α=0.10和0.05，确定每一种置信度在不同采样误差(5%，10%，15%，20%)条件下的土壤水分监测点的合理采样数目，如表5所示。

表5 土壤水分监测点的合理采样数目Tab.5 Reasonable sampling numbers for monitoring soil water content

图5 土壤水分空间分布图Fig.5 Spatial distribution of soil moisture content

由表5可知，在相同研究区域、相同置信水平情况下的合理采样数目随着采样误差的增加而减少，而在相同研究区域、相同采样误差条件下，采样数目则随着置信水平的降低而减少。固定置信水平和采样误差，随着研究尺度的增加，0～20和20～40 cm处的合理采样数目均随之增加，其中0～20 cm处的合理采样数目明显多于20～40 cm处的合理采样数目。在95%的置信水平，采样误差为5%的情况下，合理采样数目为13～83个；在90%的置信水平，采样误差为5%的情况下，合理采样数目为9～58个。

4 结 语

本文通过modis数据计算得到植被供水指数，结合实测含水率数据分析建立植被供水指数和实测土壤含水率之间的相关模型，通过该模型反演得到整个沧州地区的土壤墒情状况，并以此为基础，通过经典统计学理论和地统计学理论分析研究了沧州地区土壤水分的空间变异规律，得到以下结论。

(1)在面积较小的研究区域内，土壤含水率之间存在着一定的相关关系，而随着研究尺度(研究区域面积、采样间距)的增大，变异系数也随之增大，土壤含水率之间的相关关系逐渐减弱。

(2)小尺度的土壤水分表现了较强的空间相关性，而大、中尺度的土壤水分则表现了中等的空间相关性，随着研究尺度的增大，土壤水分的变程值增大，空间相关性逐渐减弱，由随机因素引起空间变异逐渐增强。

(3)随着研究尺度的增加，土壤各层水分监测点的取样数目亦随之增加。在95%的置信水平，采样误差为5%的情况下，合理采样数目为13～83个；在90%的置信水平，采样误差为5%的情况下，合理采样数目为9～58个。

□

[1] M Herbst B D. Modelling the spatial variability of soil moisture in a micro-scale catchment and comparison with field data using geostatistics[J]. Physics and Chemistry of the Earth, Parts A/B/C, 2003,28(6):239-245.

[2] L Brocca R M, F Melone, T Moramarco. Soil moisture spatial variability in experimental areas of central Italy[J]. Journal of Hydrology, 2007,333(2):356-373.

[3] Brocca L, Melone F, Moramarco T, et al. Spatial-temporal variability of soil moisture and its estimation across scales[J]. Water Resources Research, 2010,46(2):56-70.

[4] 张淑娟,何 勇,方 慧.基于GPS和GIS的田间土壤特性空间变异性的研究[J].农业工程学报, 2003,19(2):39-44.

[5] V V Ju′Nior M P C, J Dafonteb. Spatial variability of soil water content and mechanical resistance of BraZilian ferralso[J]. Soil & Tillage Research, 2006,85(1):166-177.

[6] 李子忠.不同尺度下农田土壤水分和无机氮的空间变异性[D]. 北京:中国农业大学, 2000.

[7] 陈 瑜.将 MODIS 遥感数据应用于墒情信息提取的研究[D]. 成都：四川大学, 2006.

[8] Lynn B H, Carlson T N. A stomatal resistance model illustrating plant vs. external control of transpiration[J]. Agricultural and Forest Meteorology, 1990,52(1):5-43.

[9] Liang Y, Zhang F, Han T. Monitoring soil humidity by using EOS/MODIS VSWI product in Qingyang[J]. Arid Meteorology, 2007,(1):7.

[10] 刘 丽,刘 清,周 颖,等.卫星遥感信息在贵州干旱监测中的应用[J].中国农业气象,1999,20(3):44-48.

[11] Yang S, Gao Y, Xu Y. Summer drought assessment based on vegetation supply water index in Chongqing[C]∥ International Conference on Remote Sensing, Environment and Transportation Engineering (RSETE 2013). Atlantis Press,2013:953-956.

[12] 陈述彭.遥感大词典[M].北京:科学出版社,1991.

[13] 雷志栋,杨诗秀.土壤特性空间变异性初步研究[J].水利学报, 1985,9(2):10-21.

[14] Miller M P, Singer M J, Nielsen D R. Spatial variability of wheat yield and soil properties on complex hills[J]. Soil Science Society of America Journal, 1988,52(4):1 133-1 141.

[15] 张仁铎.空间变异理论及应用[M].北京:科学出版社, 2005:13-19.