松花江干流依兰-佳木斯段近40年径流量时间序列分析

王春雷，邢贞相，付 强，闫丹丹，刘美鑫

(1.黑龙江省黑河水文局，黑龙江 黑河 164300；2.东北农业大学水利与建筑学院，哈尔滨 150030)

径流作为地貌形成的外营力之一，参与在地壳中的化学过程，影响土壤发育，植物生长以及湖泊、沼泽形成等。径流量作为地区工农业供水的重要来源，制约着地区社会经济的发展规模，在国民经济中具有十分重要的意义。

中国东北地区的松花江、乌苏里江、黑龙江汇流而成的三江平原腹地，是国家重要的商品粮基地的重要组成部分，2014年实现粮食总产量实现“十一连增”，对保障我国粮食安全做出了巨大贡献。近些年来，由于盲目扩展水田面积，加之农民节水意识淡薄，使得地下水位普遍下降，进而诱发了一系列水资源短缺问题。

对流域年径流量进行时间序列分析[1-3]，对研究旱涝变化规律，水资源量评估及农业水资源的可持利用都具有重要的意义。松花江干流依兰-佳木斯段地处三江平原西部，流经依兰、曙光农场、汤原农场多个国有农场，径流量是水资源重要的自然补给来源和灌溉水源。为此，陆志华[4,5]曾对松花江干流中游段的年内分配规律进行了研究，结果发现该河段径流年内分配极不均匀。为进一步获取松花江干流年径流总量的多年变化趋势性和周期性规律，本文拟采用趋势分析法、Mann-Kendall突变检验法和小波分析技术研究松花江依兰-佳木斯段的年径流量的变化特征。

1 研究区概况

松花江流域介于北纬41°42′～51°38′、东经119°52′～132°31′，流域面积为55.68万km2，约占黑龙江总流域面积的30.2%。流域西部以额尔古讷河、大兴安岭为界，海拔高度介于700～1 700 m之间；北部以黑龙江、小兴安岭为界，海拔高度介于1 000～2 000 m之间；东南部以张广才岭、完达山脉与乌苏里江、图们江等为界，海拔高度介于200～2 700 m之间；西南部以辽河、松花江的松辽分水岭为界，海拔高度介于140～250 m之间。于同江附近汇入黑龙江的松花江，与黑龙江、乌苏里江下游的广袤土地共同构成著名的三江平原。

本文主要以松花江干流依兰站、佳木斯站为研究对象，探究其径流量的时间变化特征，以期为今后工农业生产规划的制定提供依据(见图1)。

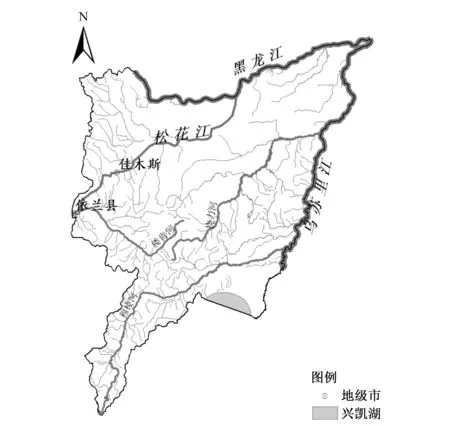
图1 研究区域概况Fig.1 The geographic location of the Sanjiang Plain

2 数据与方法

2.1 基本气象数据

径流量数据摘录自《黑龙江省水文年鉴》。根据收集的已有年鉴整理结果，分析发现1972-2010年期间的依兰、佳木斯两站的径流资料均包含丰水年13 a、平水年12 a、枯水年14 a，具有较好的代表性，因此选取该时段内的径流量观测数据作为本次研究的基础资料，通过进一步分析和计算得到依兰站和佳木斯站的年径流量。

2.2 径流量时间序列分析

本文从趋势性、突变性和周期性三方面分别对径流量时间序列分析。其中，趋势性分析采用趋势分析法，该方法能够较好地获取长序列总体变化趋势特征，但无法分析序列内部的具体突变特征，因此，本文在进行径流序列突变性分析时选用世界气象组织(WMO)推荐的Mann-Kendall突变分析法[6-9]，该方法可获取长序列内部具体突变点和突变特征；以上两种方法均无法确切地分析长序列周期性变化特征，故在分析径流序列周期性时采用Morlet小波分析法[10-13]对其进行综合判断，该方法能够准确地确定序列各个主周期，获取序列的周期性变化特征。

2.2.1趋势分析法

将样本量为n的某气候变量用xi表示，其所对应的时间用ti表示，建立用以描述xi与ti关系的一元线性回归方程：

xi=a+bi(i=1,2,…,n)

(1)

式中：a为回归常数；b为回归系数。a、b均用最小二乘法对其进行估计。

对观测数据及其所对应的时间ti、回归系数b、常数a进行最小二乘估计，分别为：

(2)

(3)

(4)

其中b为趋势分析系数。对于线性回归的计算结果，主要分析回归系数b的正负表示气候变量的趋势倾向，即b>0时x随时间t的增加呈上升趋势，b<0时x随时间t的增加呈下降趋势。b值的大小反映了上升或下降的倾向程度。

2.2.2突变分析法

设有一时间序列如下：x1,x2,…,xn构造秩序列ri，ri表示当xi>xj(1≤j≤i)时的样本累积数。定义：

(6)

sk均值E(sk)与方差Var(sk)的定义如下：

(8)

假定时间序列随机独立，对统计量UFk作如下定义：

(9)

其中UF1=0。UFk为标准正态分布，k给定一显著水平α，查正态分布表得到临界值Uα，当|UFk|>Uα，表明序列存在一个明显的趋势变化，UFk表示为UF。把此法应用到反序列中，重复以上计算过程，将计算值乘以-1得到UBk，UBk用UB表示，令UB1=0。

通过统计序列UFk和UBk可对序列x的变化趋势进一步进行分析，同时明确突变时间，指出突变区域。若UFk>0，则序列呈上升趋势；若UFk<0，则序列呈下降趋势；当它们超过临界直线时，则序列变化趋势显著。

2.2.3小波分析法

小波分析是将一簇频率各异的振荡函数作为窗口函数φ(t)对信号f(t)进行扫描和平移。时间序列f(kt)(k=1,2,…,N；Δt为取样的时间间隔)的小波变换：

(10)

式中：a为尺度因子；b为平移因子；Wf(a,b)称为小波系数。

基本小波函数涵盖墨西哥帽小波(Mexican hat)、Morlet小波和Wave小波等。本文采用Morlet小波，小波系数：

(11)

式中：c为常数；i为虚数。

它是周期函数经由Gaussian函数平滑得到，其伸缩尺度a与Fourier分析中的周期T有如下关系：

(12)

因此当取c=6.2时，周期T可以近似用a来替代。时间域上将与a相关的全部小波变换系数进行平方然后积分，即为小波方差：

(13)

式中：Var(a)为小波方差；Wf(a,b)为小波系数。

小波方差反映的是波动能量随尺度a的分布，可用以确定各尺度在一个时间序列中扰动的相对强度，与峰值处相对应的尺度即为该序列的主周期。

3 结果分析

3.1 趋势性分析

年际变化上，近40年来松花江依兰站和佳木斯站年径流量均呈下降趋势(见图2)，年际倾向率分别为-2.532 3、-5.142 4 亿m3/a。依兰站2010年径流量为603.111亿m3，同1972年径流量相比，增加了7.72%；佳木斯站2010年径流量为621.495亿m3，同1972年径流量相比，减少了10.40%。为消除周期变化对数据进行五年滑动平均，结果表明近40年来径流量无明显的总体变化趋势，呈波动状态。

图2 1972-2010年径流量总体变化特征Fig.2 The overall variation characteristics of annual runoff from 1972 to 2010

3.2 突变性分析

为进一步分析松花江依兰-佳木斯段径流量变化趋势，现采用M-K方法深入分析径流量的突变特征。M-K突变检验分析研究结果见图3(图3中虚线表示α=95%的显著性水平的临界值)。

根据图3分析可知：依兰站UF和UB两条曲线可知，依兰站径流量在1973年之前为上升趋势，1974-1983年为下降趋势，1984-2004年为上升趋势，2004年之后为下降趋势；突变发生在1975、1976和2004年。佳木斯站UF和UB两条曲线可知，佳木斯站径流量在1973年之前为上升趋势，1974-1984年为下降趋势，1985-2002年为上升趋势，2002年之后为下降趋势；突变发生在1975、1976和2000年。

综合两站径流的突变特征，两站年径流量突变点均发生在20世纪70年中期、80年代中期和21世纪初，这与20世纪70年大规模农业开垦加剧流域蒸发而致使径流量减少有关；而自20世纪80年代中期“家庭联产承包责任制”实施以来，农业种植积极性得到极大提高，中国农业产业结构调整初见成效，农业生产力极大发展，工农业水资源消耗量剧增，致使年径流量恢复能力减弱；21世纪初，随着黑龙江省粮食产能的连续提升，水资源用量尤其是水稻种植面积进一步扩大，加之水利工程建设日益增多，致使研究河段的年径流复又下降，为此，黑龙江省正在大力推进“节水增粮食”行动、积极推广“水稻节水控制灌溉技术”和加快“两大平原”现代农业综合配套改革实验方案的实施，以提高水资源的利用效率。

图3 年径流量M-K突变分析结果Fig.3 The M-K mutation analysis on annual runoff

3.3 周期性分析

图4为小波变换系数实部时频分布图，从图4可以看出，近40 a来松花江依兰站和佳木斯站包含了不同尺度的周期变化。图5为松花江依兰站、佳木斯站Morlet小波方差分布，可对图4中所识别出的周期进一步判断。综合分析图4和图5可知：18、8和5 a左右尺度波动相对较为明显，存在径流量偏多偏少的循环变化，且2010年后上述尺度的小波正在形成且为正值，因此预测在这3种尺度上未来径流量均呈现偏多趋势。

图4 小波变换系数实部的时频分布Fig.4 The time-frequency distribution of real parts of wavelet transform coefficient

图5 小波变换方差Fig.5 The variance distribution of real parts of Morlet wavelet

本文得出的佳木斯站年径流序列趋势分析结果和突变分析结果与文献[4]的研究成果具有较好的一致性。此外，与文献[4]相比，本文延长了径流序列长度，同时增加了依兰站进行对比分析，使本文结果可靠性更强。

4 结 语

本文运用松花江干流依兰站和佳木斯站1972-2010年逐年径流量资料，采用趋势分析法、Mann-Kendall突变分析法和Morlet小波分析法，对松花江依兰-佳木斯段年径流量进行时间序列分析，得到出以下几点结论。

(1)年际变化上，近40 a来松花江依兰站和佳木斯站年径流量表现出总体微弱下降趋势，且伴随明显的波动特性。这与全球气候变暖使蒸发加剧和水文过程的周期性有密切关系。

(2)时间突变上，两站年径流量均存在多个 突变点，且突变点具有较好的同步性，这与该地区的人类活动、社会生产力和上下游的水文联系有极大关系。因此，欲控制年径流的突变，应从规范人类活动、推广高效节水技术等方面入手，同时要注意考虑上下游的影响。

(3)周期变化上，松花江依兰站和佳木斯站包含了不同尺度的周期变化，18、8和5 a左右尺度波动相对较为明显，存在径流量偏多偏少的循环变化，且2010年后上述尺度的小波正在形成且为正值，因此预测在这3种尺度上未来径流量均呈现偏多趋势。

□

[1] 王 英,曹明奎,陶 波,等. 全球气候变化背景下中国径流量空间格局的变化特征[J]. 地理研究,2006,25(6):1 031-1 040.

[2] 袁 喆,严登华,杨志勇,等. 1961-2010年中国400 mm和800 mm等雨量线时空变化[J]. 水科学进展,2014,25(4):494-502.

[3] 徐利岗,周宏飞,梁 川,等. 中国北方荒漠区降水多时间尺度变异性研究[J]. 水利学报,2009,40(8):1 002-1 011.

[4] 陆志华，夏自强，于岚岚. 松花江佳木斯站径流变化规律及演变趋势分析[J].水电能源科学，2011,29(4)：14-17.

[5] 陆志华，夏自强，于岚岚，等.松花江干流中游段年内分配变化规律[J].河海大学学报(自然科学版)，2012,40(1)：63-69.

[6] 胡 刚,宋 慧. 基于Mann-Kendall的济南市气温变化趋势及突变分析[J]. 济南大学学报(自然科学版),2012,26(1):96-101.

[7] Z X Xu, K Takeuchi, H Ishidaira. Monotonic trend and step changes in Japanese precipitation[J]. Journal of Hydrology, 2003,279(3):144-150.

[8] Henry B Mann. Nonparametric tests against trend[J]. Econometrica, 1945, 13(3):245-259.

[9] M G Kendall. Rank correlation methods[M]. London: Charles Griffin, 1948: 202.

[10] 邵晓梅,许月卿,严昌荣. 黄河流域降水序列变化的小波分析[J]. 北京大学学报(自然科学版),2006,42(4):503-509.

[11] 祝青林,张留柱,于贵瑞,等. 近30年黄河流域降水量的时空演变特征[J]. 自然资源学报,2005,20(4):477-482.

[12] 刘 勤,严昌荣,张燕卿,等. 近50年黄河流域气温和径流量变化特征分析[J]. 中国农业气象,2012,33(4):475-480.

[13] 李占杰,鱼京善. 黄河流域降水要素的周期特征分析[J]. 北京师范大学学报(自然科学版)，2010，46(3):401-404.

[14] 邢贞相，闫丹丹，刘美鑫，等. 三江平原近60年降水量时空变异特征分析[J]. 农业机械学报,2015,46(11):337-343.