基于SAMCEF Rotor的高速泵转子临界转速分析

段小辉，孔繁余，冯子政，黄 丹，宋艳文( 江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 03； 哈尔滨电机厂有限责任公司，哈尔滨 50040)

0 引 言

为确保机器在工作转速范围内不致发生共振，临界转速应适当偏离工作转速。尽量避免转子在受到某种激励之后产生的共振给转子带来的严重损坏。国内外很多学者在转子动力特性研究领域进行过大量的探索，内容十分广泛[1-4]。王海朋[5]等针对某小型涡喷发动机转子的实际结构，在ANSYS中建立了三维有限元模型，计算了前两阶固有模态和振型，并对转子的临界转速进行了计算；在热度场对转子系统临界转速的影响上，朱向哲[6]等利用热-结构-动力学耦合理论，对某汽轮机转子临界转速的影响进行了探讨；叶大庆[7]等应用影响系数法研究支撑刚度对轴系临界转速影响。周文霞[8]计算分析了核主泵的地震谱响应以及转子的临界转速。这些研究方式沿用传统的转子动力学分析即采用传递矩阵方法进行，由于将大量的结构信息简化为极为简单的集中质量——梁模型，不能确保模型的完整性和分析的准确度，同时忽略了轴承的周向刚度和阻尼，且转子的“陀螺效应”一直是制约转子动力学有限元分析的瓶颈问题。有限元软件ANSYS虽然解决了动力特性分析中“陀螺效应”影响的问题，但是其计算过程需要编写命令流，直观性较差，对于初学者来说，掌握起来比较困难[9-12]。专业的转子动力特性分析软件SAMCEF Rotor能够较好的解决这些问题，可以极大地提高工作效率[13]。

1 有限元模态分析理论

模态分析是研究结构动力特性的一种近代方法，是系统辨别方法在工程振动领域的应用，其主要用于确定设计结构或机器部件的振动特性，即结构的固有频率和振型，它们是承受动载荷结构设计中的重要参数。模态分析的实质是计算结构振动方程的特征值和特征向量[14]。

动力学基本方程可表示为：

[M]+[C]+[K]{U}={F(t)}

式中：分别为各质点的加速度、速度和位移向量；[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；{F(t)}为载荷向量。

采用有限元方法计算转子临界转速时，转子会出现正进动和反进动。由于陀螺效应的作用，随着转子自转角速度的提高，反进动固有频率降低，而正进动固有频率将提高。根据临界转速的定义，应只对正进动固有频率进行分析[15]。在后处理中首先剔除反进动固有频率，然后分析各阶模态模型确定同一阶振型的正进动与反进动固有频率。改变转子自转角速度ω，计算出新的进动角速度Ω，最后画出曲线Ω～ω，即转子坎贝尔曲线。根据临界转速定义，当Ω=ω时，Ω即所求临界转速。

2 模型建立

2.1 结构与参数

本次设计的高速矿用抢险泵结构如图1所示，其中转子系统的主要部件有泵主轴、叶轮、轴套、推力盘、电机转子、副叶轮等。性能参数：流量Q=150 m3/h，扬程H=700 m，转速n=6 000 r/min，配套功率P=600 kW。

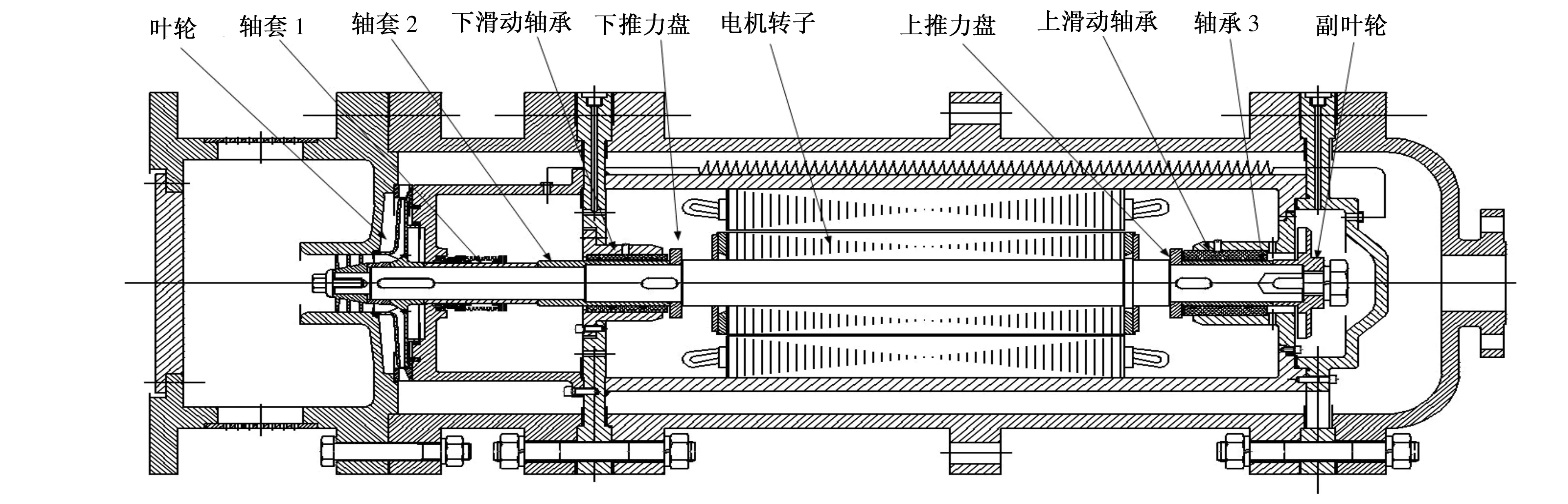
图1 高速矿用抢险泵结构图Fig.1 The structure of High-speed mine rescue pump

2.2 三维造型及材料特性

根据高速泵转子系统各部件的二维图，利用UG软件对转子的主要部件进行三维造型，并结合图1将转子系统各部件进行装配，高速矿用抢险泵的转子系统三维模型如图2所示。利用UG的模型分析功能定义各部件的密度、计算各部件的质量及转动惯量等，转子部件的材料特性及质量属性分析如表1所示。

图2 高速泵转子系统三维模型图Fig.2 3D model of rotor system

表1 转子各部件材料特性Tab.1 Material characteristics of rotor system

2.3 轴承的支承模型建立

轴承对于转子系统的动力特性影响很明显，轴承是阻尼的主要来源，控制着转子的响应；轴承的刚度和阻尼又影响着转子的临界转速和稳定性。轴承动力学模型如图3所示，其中kxx、kyy和cxx、cyx为主刚度系数和主阻尼系数；kxy、kyx和cxy、cyx为交叉刚度系数和交叉阻尼系数，它们表示液膜力在两个互相垂直方向的耦合作用，交叉动特性系数的大小和正负在很大程度上影响着轴承工作的稳定性。 本次模拟的湿式电机径向轴承动力学特性参数由哈尔滨电机厂有限责任公司提供，如表2所示。其中，输入轴承刚度矩阵需要注意，Samcef中轴承刚度矩阵为6×6矩阵，其中1、2和3为位移刚度，4、5和6为转角刚度。对角线的主位移刚度为11、22和33。程序规定11和22为垂直于旋转轴方向，33为沿着旋转轴方向。轴承单元参数设置如图4所示。

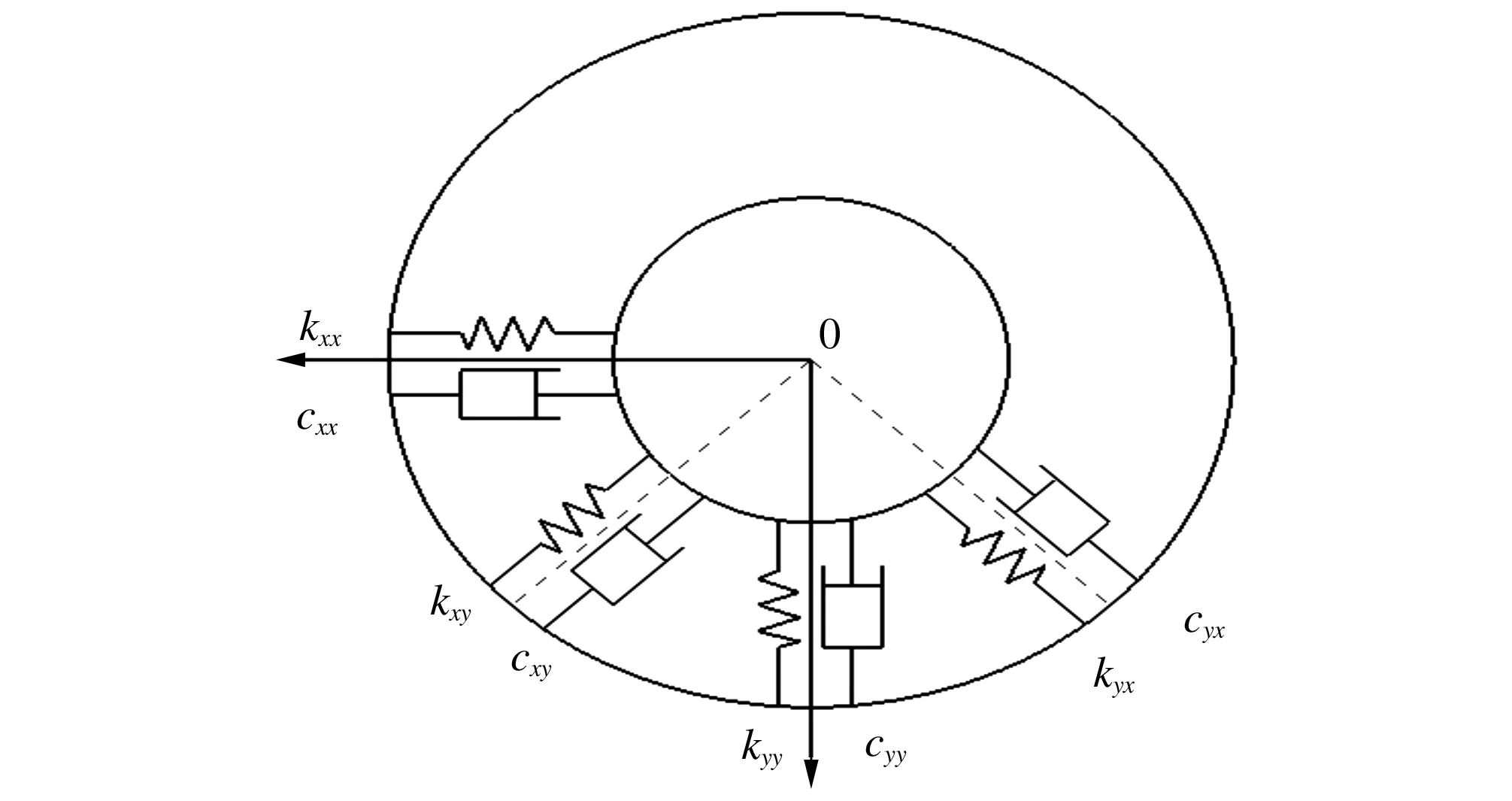
图3 轴承动力学模型Fig.3 Dynamical model of bearings

图4 轴承单元参数设置Fig.4 Parameters of bearing units

表2 轴承支承刚度(N/m)和阻尼(Ns/m)Tab.2 Bearing stiffness(N/m) and damping(Ns/m)

3 临界转速及振型分析

SAMCEF Rotor软件有三种有限元模型可用来描述转子系统。

(1)一维模型：转子系统用梁，弹簧和集中质量单元来模拟，该模型计算速度快，适用于有大量参数需要调整的初期设计分析。

(2)二维傅里叶级数模型：转子采用2D傅里叶多谐波单元模拟。该模型适合创建旋转设备更精细的计算分析模型，以及带有多数目叶片的旋转机械的建模。

(3)三维模型：采用三维实体建模，用体单元(六面体、棱柱或四面体)或者壳单元描述转子系统。

分别采用以上三种模型对临界转速及振型进行比对和分析。其中，一维和二维模型需要将转子系统各部件作为集中质量单元处理，利用UG的模型分析功能计算出各部件集中质量特性如表3所示。

表3 转子系统各部件集中质量特性Tab.3 The lumped mass of rotor system

3.1 一维模型转速及振型

利用SAMCEF Rotor软件建立转子系统的梁-轴承-集中质量单元模型，根据实际情况将转子系统中的轴承单元设置为弹性支承，定义轴承的动力特性系数，对转子系统进行模态分析。弹性支承转子系统的前三阶临界转速及振型和坎贝尔图如图5所示。

图5 一维模型临界转速、振型及坎贝尔图Fig.5 Critical speed、vibration mode and Campbell chart of 1D model

3.2 二维模型临界转速及振型

二维模型采用轴对称傅里叶级数展开单元模拟转子。这种单元可以更好地模拟转子的结构和特性。集中质量和转动惯量采用lumped mass(集中质量单元)，轴承支承单元采用Ground Bearing(接地轴承单元)模拟，设置轴承的刚度矩阵和阻尼矩阵。二维模型的前三阶临界转速及振型和转子系统坎贝尔图如图6所示。

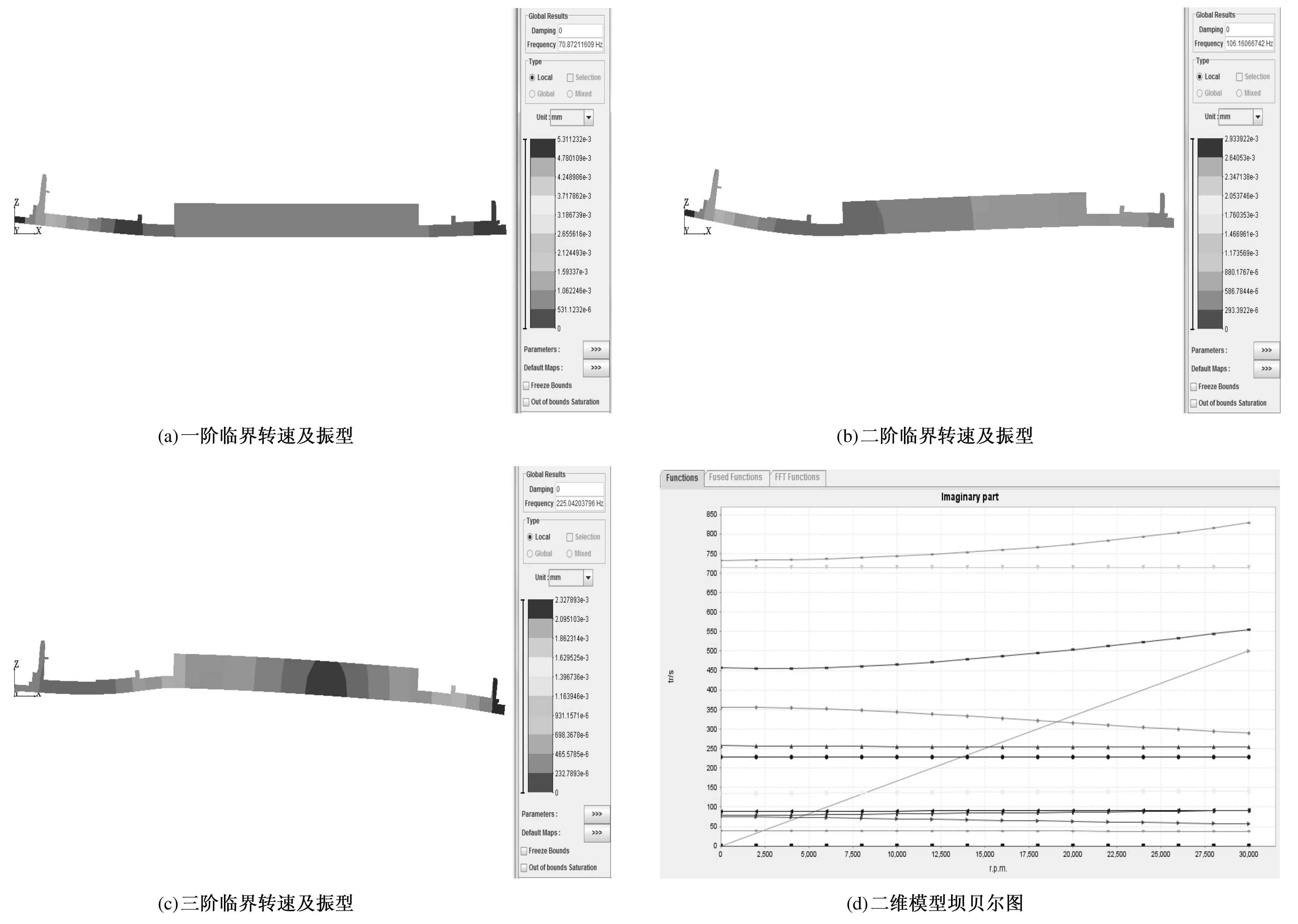
图6 二维模型临界转速、振型及坎贝尔图Fig.6 Critical speed、vibration mode and Campbell chart of 2D model

3.3 三维模型临界转速及振型

在三维模型中，各转动部件之间均采用Glue(黏接)方式，即假设转子各部件的接触位置不发生松动，并且在单元特性或者材料特性定义时可以区分开。若使用布尔运算处理，各个部件将成为一个几何体，无法区分不同的材料特性。在SAMCEF Rotor中进行装配，定义材料属性及约束条件，并进行网格划分。三维模型的前三阶临界转速及振型和转子系统的坎贝尔图如图7所示。

图7 三维模型临界转速、振型及坎贝尔图Fig.7 Critical speed、vibration mode and Campbell chart of 3D model

3.4 模拟结果对比分析

从模型大小和计算时间对比可知，采用一维和二维模型所表示的自由度与三维模型相当，说明三者对转子结构的描述基本一致，但在节点数和CPU计算时间上，一维和二维模型明显占优，减少了对计算机资源的占用，节省了大量的计算时间。

从不同模型的振型对比可知，一阶临界转速以转子前部的振动为主，表现为离心叶轮的摆动；二阶临界转速以转子前部和后部的振动为主，表现为离心叶轮和副叶轮的摆动；而第三阶临界转速以转子中部的振动为主，表现为电机转子的摆动。不同模型在相同临界转速所表现出来的振型基本一致，体现了模型建立及结果分析的准确性。

不同模型的各阶临界转速对比如表4所示。从不同模型的坎贝尔图和临界转速的对比可知，选用一维及二维模型和选用三维模型进行计算所反映的临界转速分布基本一致。转子系统各阶正、反进动固有频率都是稳定的，随着转子转速的提高，各阶正进动固有频率将逐渐上升，而各阶反进动固有频率将逐渐下降。在不平衡力驱动下，转子将作正向同步涡动，由临界转速的定义，对于正向同步涡动的临界转速应予以重视，故只对正进动固有频率进行分析。如前所述，一维及二维模型将叶轮等简化为集中质量施加于主轴上，如果转动惯量很大，采用这种描述方式就会带来一定的误差。转动惯量分为极转动惯量(绕转子转轴)和直径转动惯量(绕轮盘任一直径)，本文的算例中，一阶临界转速表现为离心叶轮的摆动，二阶临界转速表现为首尾两端的摆动，摆动是直径转动惯量的体现，通过计算，离心叶轮的直径转动惯量是副叶轮的10.1倍，由于一阶临界转速主要受离心叶轮的影响，二阶临界转速同时受到离心叶轮和副叶轮的影响，理论上离心叶轮简化后引起的临界转速误差应该比副叶轮引起的临界转速误差大。同样，由于一维和二维模型采用集中质量单元，相比三维模型采用实体也会产生误差。

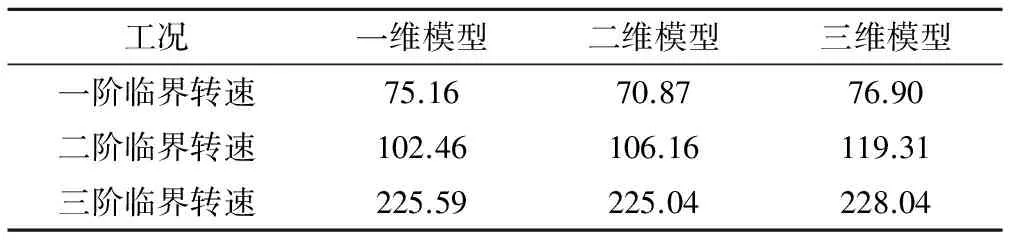
表4 不同模型临界转速计算结果 HzTab.4 Critical speed of different models

针对模拟的高速矿用抢险泵而言，转子系统运行到额定工作转速将经过一阶临界转速，最大振幅1.3 mm，能够在额定工作转速范围内平稳运行，且额定工作转速n=6 000 r/min远离临界转速，可知本文研究的高速矿用抢险泵转子系统能够在额定转速下安全运行。

4 结 论

(1)通过SAMCEF Rotor软件对高速矿用抢险泵转子系统进行初步的动力学特性分析，得到了临界转速和转子的振型变化情况，表明该设计方案能够满足转子系统的动力学设计要求。

(2)对于复杂的结构设计及需要反复修改的初始设计阶段，SAMCEF Rotor一维梁单元模型和二维傅里叶单元模型较三维实体模型更加简便和实用。基于SAMCEF Rotor转子动力学软件通过不同的模型进行临界转速的计算和对比分析，证明其计算结果精度较高。

(3)建议在工程研制初期，采用一维及二维模型计算临界转速及振型，便于尽快对方案进行筛选和调整，避免工作转速达到临界转速产生共振现象。在详细的设计结构完成后，选用三维实体模型进行临界转速的计算，通过三维实体的振型图可以更好地观察转子系统外缘如叶轮出口的振动情况，通过计算仿真数据为实际试验提供参考和理论依据。

□

[1] Gautam Das，Ashok Kumar Ray，Sabita Ghosh. Fatigue failure of a boiler feed pump rotor shaft[J]．Engineering Failure Analysis，2003,10(6):725-732．

[2] Stephan Nackel，Per Karlsson． Submerged vertical safety concept [J].World Pumps, 2009,513:12-15．

[3] Bert R． Jorgensen，Yung C． Shin． Dynamics of Machine Tool Spindle /Bearing Systems under Thermal Growth[J].Journal of Tribology，1997，119 (10):875-882．

[4] Qiu Baoyun，Lin Haijiang，Yuan Shouqi． Guide bearing probability load theory of large vertical pump[J]．Mechanism and Machine Theory，2007，42(9):1 199-1 209．

[5] 王海鹏，戴 勇，张志清，等.基于ANSYS的发动机转子临界转速计算[J].航空发动机，2009,35(5)：30-31.

[6] 朱向哲，袁惠群，贺 威.稳态热度场对转子系统临界转速的影响[J].振动与冲击，2007,26(12)：113-116.

[7] 叶大庆，张 雷，林建中，等.支承刚度对600 MW汽轮机发电机临界转速的影响[J].振动与冲击，2004,23(2)：61-63.

[8] 周文霞.核主泵地震谱响应及转子临界转速分析[D].上海：上海交通大学，2010.

[9] 王宁峰，王桂红.基于ANSYS的转子临界转速计算[J].青海大学学报，2007,25(5)：18-21.

[10] 曹卫东，高 一，王秀兰，等.基于ANSYS的矿用潜水电泵转子系统的优化设计[J].排灌机械工程学报，2012,30(2)：157-161.

[11] 汪家琼，孔繁余，钱永康.多级离心泵临界转速计算分析[J].矿山机械，2014,42：56-59.

[12] 孔繁余，陈 浩，王 婷，等.基于流固耦合的减压塔底泵强度分析[J].机械工程学报，2013,49(2)：159-164.

[13] 周传月.SAMCEF有限元分析与应用实例[M].北京：机械工业出版社，2009.

[14] 顾家柳等.转子动力学[M].北京：国防工业出版社，1985.

[15] 钟一諤，何衍宗，王 正，等.转子动力学[M].北京：清华大学出版社，1987.