基于灰色理论及BP神经网络的尿素水解预测模型研究
雷 涛,孙西欢,马娟娟,郭向红,冯 玚,王宏宇
(太原理工大学水利科学与工程学院,太原 030024)
尿素具有价格低廉[1]、高含氮量[2]、安全等诸多优点,因此它成为了农业生产中使用最为广泛的氮肥之一。但不合理的施用同样也会引起作物烧苗,氮素气态损失[3],环境污染等问题[4]。因此,开展不同水热条件下尿素水解定量研究,对于揭示尿素水解动力学特性,提高氮素利用效率等方面都具有重要的作用和意义。
尿素进入土体后,会在土壤脲酶催化作用下发生水解反应,水解过程如下:

(1)
土壤尿素水解是一个较为复杂的化学反应过程,常受到温度[5],含水量[5],施肥方式[6],尿素颗粒大小[7],土壤类型[8],施肥浓度[9]等诸多因素的影响。国内外学者围绕这些因素开展了一系列的试验研究,取得了丰硕的研究成果,这方面的研究多集中在定性分析方面。尿素水解动力学模型研究方面,有部分学者认为尿素水解过程符合米氏动力学或者零级动力学模型[5]。传统的参数估算法进行参数估计时最大的困难就在于样本点过少,很难保证其预测精度,但灰色预测理论的处理方法能有效避免小样本的限制,预测精度相对较高。BP神经网络具有较强的非线性映射能力,高度的自学习和自适应能力,以及出色的泛化能力和容错能力。基于灰色理论及神经网络理论的尿素水解定量预测研究也未见相关报道。本研究通过室内培养试验,定时监测土壤尿素水解动态变化过程,结合灰色理论算法与BP神经网络算法,旨在构建不同水热条件下的尿素水解定量预测模型。
1 材料与方法
1.1 试验材料
土壤样品采自山西省太谷县有代表性的果园土壤,取土深度为30~200 cm,将各深度土壤样品中的石头、根系等杂物剔除后,带回实验室,阴凉处风干后,过2 mm筛备用。土壤质地为沙壤土,pH值为8.84,含水率21.6 g/kg,田间持水量217.8 g/kg,硝态氮含量0.41 mg/kg,铵态氮0.59 mg/kg。
1.2 试验设计
本试验采用室内培养法,进行不同含水量、温度条件下土壤尿素水解试验研究,含水量设3个水平(W60,W80,W100),分别为60%、80%、100%田间持水量;培养温度设4个水平(T15,T20,T25,T35),包括15、20、25、35 ℃,采用全面试验设计,共12个处理,每个处理设置3个重复。采用称重法补充培养过程中损失的水分,并分别间隔24 h对土壤进行取样,采用液相色谱法测定各处理下的土壤尿素残余量。
1.3 模型建立
1.3.1BP神经网络
本研究采用3层BP神经网络对尿素态氮含量进行预测,主要包括输入层、隐含层和输出层。选取温度、含水量、时间作为输入因子,尿素态氮含量作为输出因子,本文所构建的拓扑结构为3-2-1,其中,隐含层包括2个单位(图1)。在水热耦合条件下尿素态氮动态含量数据集中,选取70%的样本数据作为训练集,其余30%的样本数据作为预测集。因此,训练样本数为53,预测样本数为22。网络中间层神经元传递函数采用双曲正切函数,输出层神经元传递函数采用恒等函数,优化算法采用调整的共轭梯度法。训练目标误差为0.000 1。

图1 尿素水解BP神经网络模型结构图Fig.1 BP neural network structure of Urea hydrolysis
1.3.2Verhulst灰色预测模型
对土壤尿素态氮含量进行等时距测定,定义X(0)(i)为i次观测的尿素态氮含量,即:
X(0)=[X(0)(1),X(0)(2),…,X(0)(n)]
(2)
对观测数据X(0)(i)作一次累加,得到:
X(1)=[X(1)(1),X(1)(2),…,X(1)(n)]
(3)
式中,X(1)(k)=∑ki=1X(0)(i),k=0,1,…,n。
Verhulst灰色预测模型方程为:
(4)
式中:a为发展系数;b为灰色作用量。
上式的唯一解为
(5)
式中:X(1)(1)=X(0)(1)为初值,该式为尿素态氮含量计算及预测模型。
根据最小二乘法和极值原理求解,灰色Verhulst 模型的参数向量为:
[a,b]T=(BTB)-1BTY
(6)
参数矩阵为:
(7)
YT=[X(0)(2),X(0)(3),…,X(0)(n)]
(8)
式中:B、Y为与X(1)(i)和X(0)(i)相关的模型参数矩阵。
1.3.3零级动力学模型
化学反应动力学是研究反应速率和机理历程的科学。零级动力学模型是动力学机理模型中最简单的一种形式。目前,零级动力学模型在土壤尿素水解中的应用比较常见,其模型如式(9)所示。在零级反应中,反应物浓度随时间呈现线性下降趋势,反应速率并不随时间的变化而变化。常见的零级反应包含了脲酶催化水解反应,反应速率取决于脲酶催化剂的有效表面活性位或酶的浓度。
(C0-Ct)=a-Kt
(9)
式中:C0、Ct分别为初始及t时刻的尿素态氮含量,mg/kg;a为系数;K为水解速率常数,mg/(kg·d);t为水解时间,d。
1.4 模型评价指标
对模型预测性能的评价指标包括:决定系数R2,平均相对误差MAPE,相关系数r,其计算公式如下:
(12)

2 结果分析
2.1 灰色理论模型
如表1所示,为不同水热条件下尿素水解Verhulst灰色预测模型参数及模拟精度。图2为Verhulst模型的模拟值与实测值相关性图。结合表1及图2,可以看出,两者的相关系数分别达到了0.989 6~0.999 2,均在0.01水平下极显著相关,相关性方程的斜率为0.983 9~1.040 3,这充分说明了模拟值与实测值之间具有较好的一致性。经计算,分别在15、20、25、35 ℃时,平均相对误差介于4.83%~8.74%,2.87%~3.05%,5.94%~14.46%,13.13%~32.53%,说明在低温时(15~25 ℃),Verhulst模型的模拟相对误差较小,但到35 ℃时,模拟效果会明显变差。决定系数(R2)达到了0.979 0~0.997 0。并对模拟值与实测值的差异性进行配对t检验,经计算,在不同水热条件下,|t|值全都小于t检验临界值,p值也全都大于0.05,结果表明两者之间并无统计学差异。综上所述,模拟值与实测值之间具有较好的一致性和较高的模拟精度,可以用于模拟土壤尿素水解动态变化过程。

表1 尿素水解Verhulst灰色预测模型参数及模拟精度表[t0.05(8)=1.860, t0.05(5)= 2.015, t0.05(3)= 2.353]

图2 尿素水解Verhulst灰色预测模型模拟值与实测值相关性分析Fig.2 Relativity analysis between simulated and measured values of Urea hydrolysis
2.2 BP神经网络模型
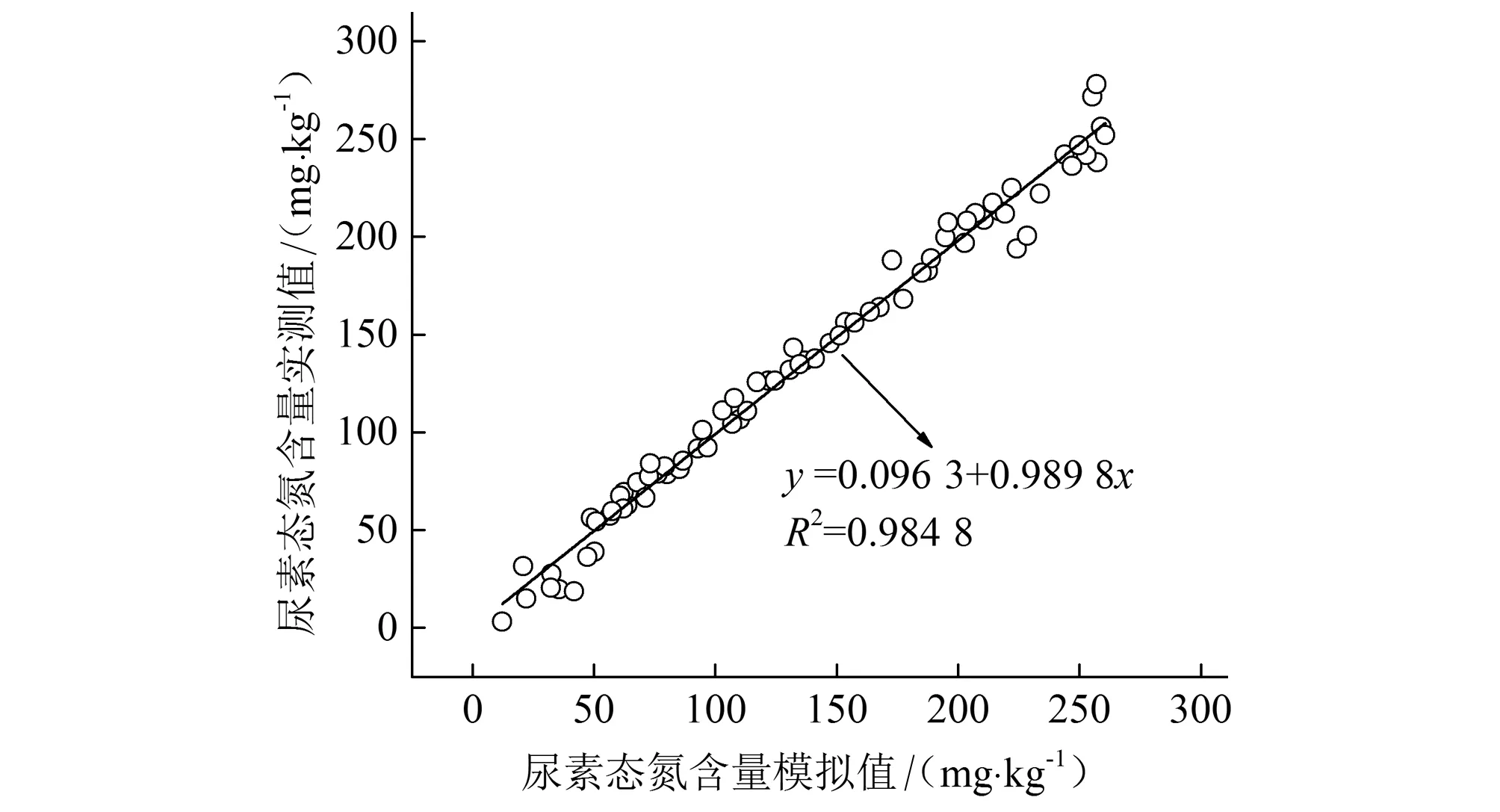
图3 尿素水解BP预测模型模拟值与实测值相关性分析Fig.3 Relativity analysis between simulated and measured values of Urea hydrolysis

rMAPE/%R2t值Sig0.99242.39000.9845-1.22120.2258
BP模型的预测值与实测值相关性如图3及表2所示。预测值和实测值之间呈极显著(p<0.01)的线性相关,相关系数达到了0.992 4。模拟值与实测值的决定系数为0.984 5。BP神经网络法预测值与实测值之间存在一定程度的误差,训练集和预测集的平均相对误差分别为1.16%和2.39%,并对模拟值与实测值之间的差异性进行配对t检验,经计算|t|
2.3 零级动力学模型
结合尿素水解动态变化曲线以及各个动力学模型特点,认为本研究中尿素水解过程可用零级动力学模型表示,反应速率、动力学常数项与水热之间关系均用Rational2D模型表示,并且决定系数R2分别达到0.972 1,0.991 5。将此关系代入零级动力学模型中, 得到供试土壤不同水热条件下的尿素水解动力学方程,如表3所示。零级动力学预测值与实测值之间的相关系数达到0.991 2,并已达到极显著水平。模拟值与实测值的决定系数、平均相对误差分别为0.984 5和13.27%。经配对t检验结果表明,模拟值与实测值之间的差异性并未达到显著水平。说明该模型也可用于预测尿素水解动态变化过程。

表3 包含温度、含水量因子的尿素水解零级动力学模型[t0.05(74)=1.993]
2.4 不同模型比较
如图4所示,分别采用3种模型对尿素态氮含量进行预测,并与实测值进行对比研究。在15 ℃时,对于同一含水量条件时,初始时刻,3个模型的模拟效果基本相当,在中间时刻(2~7 d),零级和灰色模型会出现比真实值偏大问题,BP模型仍能与真实值保持一致,在序列末端时BP模拟出现略微不稳定状况。在60%与80%田间持水率时,3个模型的差异比较明显,在100%田间持水率时,零级模型与灰色模型模拟效果基本接近[图4(a)];在20 ℃时,三者模拟效果基本接近,灰色预测模型预测效果会更好一些[图4(b)]。25与35 ℃时,零级与灰色预测模型离实测值偏离会更为明显,而BP模型具有良好的稳定性,模拟效果占优势地位[图4(c)、(d)]。
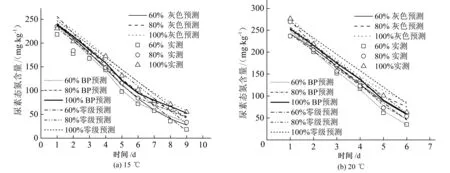

图4 不同预测模型的模拟值与实测值比较Fig.4 Comparison of measured values and simulated values calculated by different models
由图4及表1~表3看出,BP、灰色和零级3个模型的预测值与实测值之间的决定系数大小为:灰色(0.990 6)>BP(0.984 5)>零级(0.974 9),BP模型的平均相对误差明显小于其他两个模型。说明对于同一时间序列,预测模型不同导致预测结果也截然不同;在15、20、25 ℃时,灰色模型的平均相对误差基本小于10%,在35 ℃时数值会增大到13.13%~32.53%。零级模型同样存在随温度升高,模拟精度下降的问题,说明对于不同的时间序列,相同的预测模型预测精度也并不相同。综上所述,预测效果不仅与预测模型有关,还与时间序列本身有关。从图4还可以看出,灰色预测模型和零级预测模型相对实测值会普遍偏大,后者偏离更为严重一些。而BP神经网络的绝对误差有正有负,说明BP神经网络预测模型对尿素态氮含量的预测是均衡的,不会总是预测偏大或者总是预测偏小的现象。
灰色模型在20 ℃的预测效果较好,与真实值吻合较好,在15 ℃时预报误差较大的时期主要集中在时间序列的中段,25与35 ℃条件时,整体偏差都较大,零级模型具有相似的特点。BP模型整体偏差都较小,较大相对误差出现在序列初始及末端时刻。造成误差的可能原因:本研究中土壤含水率是采用称重法,通过逐日补水来维持设计水平的;在序列末端,尿素态氮含量非常低;预测模型的机理并不完全符合尿素水解机理,具体算法有待改进等。这些因素可能会导致模拟值与实测值存在一定偏差。
综合以上分析可知,良好的样本拟合效果并不能代表一个好的预测结果,因此在使用模型进行实际预测之前,需要不断确认模型预测方法。鉴于误差分析和精度比较,3种不同模型的模拟效果好坏呈现如下关系:BP>灰色>零级。并且BP的预测结果相对误差仅为2.39%,其预测效果要显著优于零级模型和灰色预测模型。表明上述建立的BP预测模型合理可靠,能有效表征土壤尿素水解动态变化情况。因此在尿素水解定量研究中,建议使用BP模型进行预测。
3 结 论
针对土壤尿素水解定量预测问题,采用Verhulst灰色模型,BP神经网络模型,以及零级动力学模型进行了预测模拟,对模拟精度和模型适用性进行了验证和评价,对模拟结果进行了误差分析,并对3种模型的模拟效果进行了比较。结果表明,3种模型基本都能满足尿素水解动态变化过程的预测精度要求,误差可能由试验系统误差和模型算法等原因造成,3种模型的预测效果好坏表现为:BP>灰色>零级,BP模型的预测结果相对误差仅为2.39%,BP神经网络预测模型具有更好的非线性拟合能力和更高的预测精度。土壤内部环境极其复杂,影响尿素水解的因素相对庞杂,如何确定尿素水解关键影响因子,并在此基础上,将筛选好的因子作为BP模型输入端,从而提高模拟精度有待进一步研究,此外,多种预测模型的相互结合,以及模拟算法的改进,也是进一步的研究方向。
[1] Campana M,Alves AC,Anchão de oliveira PP, et al. Ammonia Volatilization From Exposed Soil and Tanzania Grass Pasture Fertilized with Urea and Zeolite Mixture[J]. Communications in Soil Science and Plant Analysis, 2015, 46(8):1 024-1 033.
[2] Glibert PM,Harrison J,Heil C, et al. Escalating worldwide use of urea-a global change contributing to coastal eutrophication[J]. Biogeochemistry, 2006,77(3):441-463.
[3] Rodhe L,Pell M,Yamulki S. Nitrous oxide, methane and ammonia emissions following slurry spreading on grassland[J]. Soil Use and Management, 2006,22(3):229-237.
[4] Rodhe H,Dentener F,Schulz M. The global distribution of acidifying wet eeposition[J]. Environmental Science & Technology, 2002,36(20):4 382-4 388.
[5] 李世清,李生秀. 影响土壤尿素水解速率的一些因子[J]. 植物营养与肥料学报, 1999,5(2):156-162.
[6] 戴腾飞,席本野,闫小莉,等. 施肥方式和施氮量对欧美108杨林地土壤氮素垂向运移的影响[J]. 应用生态学报, 2015,26(6):1-8.
[8] 冉 炜,沈其荣,郑金伟. 尿素浓度, 培养时间和温度对3种土壤尿素水解过程的影响[J]. 南京农业大学学报, 2000,23(2):43-46.
[9] 汪建飞,盛 蒂,段立珍. 土壤外源尿素水解速率影响因子研究[J]. 安徽技术师范学院学报, 2004,18(5):15-20.

