可靠性理论在强风化岩石边坡稳定性分析中的应用

徐根洪

（浙江树人大学城建学院，杭州 310015）



可靠性理论在强风化岩石边坡稳定性分析中的应用

徐根洪

（浙江树人大学城建学院，杭州 310015）

摘 要：为了对强风化岩块组成的岩石边坡的稳定性进行评价，通过一次二阶矩法、蒙特卡罗模拟和有限差分数值分析相结合的方法对其进行了可靠性分析和研究。首先，将岩石边坡等效为连续介质体，利用等效连续模型获得强风化岩石边坡的特征参数，之后，将岩石边坡的岩土材料参数定义为二维空间变异参数，并通过一次二阶矩法建立了变异参数的不确定性模型；然后，利用蒙特卡罗模拟了岩土参数的空间变异性；最后，利用有限差分的方法研究了协方差、相关距离对安全系数和可靠性指标的影响。结果表明：岩土工程参数空间变异性对特定岩石边坡的稳定性评价具有很大的影响；强风化岩石边坡的安全性评价不能仅凭单一参数值确定；随着岩石边坡参数协方差的增大，可靠性指标值逐渐减小，安全系数逐渐减小；随着自相关距离的增大，可靠性指标逐渐增大。因此，应在边坡常规分析和设计过程中充分考虑岩土工程参数空间变异性。

关键词：岩石边坡；可靠性分析；强风化；空间变化特性；稳定性

1 研究背景

边坡安全性问题作为岩土工程界的重要研究课题，长期以来一直得到学者和工程师们的重视。边坡岩体处于自然环境中，持续遭受风吹日晒、冰冻雨淋等风化作用，显著降低原岩的力学性质，易造成边坡的变形或失稳。无论是岩石边坡还是土质边坡都可能发生失稳问题，即使是过去长期处于稳定状态的边坡也会突然发生失稳。此外，强风化岩块组成的岩质边坡更易于失稳，因此对其进行稳定性评价显得尤为重要。

众所周知，岩土工程最主要的特性是岩土体的不确定性和不确定性诱发的相关风险。岩土工程系统是一个受到多空间变化、多因素作用下的复杂系统，其复杂性特征在于它具有独特的非确定性。在岩土工程实践中，不确定性因素主要来源于以下3个方面：①自然异质性或固有的可变性（物理现象导致的变化）；②测量误差（由于设备、随机测试产生的错误）；③模型转换的不确定性（与设计参数相关的基于经验、半经验或理论模型的估算）。近年来，概率方法在岩土工程及其相关领域中得到了广泛的应用，国内外学者对这方面进行了一系列的研究工作，如：谭晓慧［1］和杨建贵等［2］对边坡稳定性问题进行模糊随机可靠性分析；王宇等［3］利用模糊点估计法对边坡进行模糊随机可靠性分析；杨坤等［4］对边坡块状结构岩体进行模糊随机可靠性分析；王亚军［5］、蒋建群等［6］、贾厚华等［7］、付士根［8］和陆黎斌等［9］对边坡进行模糊随机可靠度分析；Dodagoudar等［10］利用模糊集理论分析了边坡的可靠性；Giasi等［11］利用概率和模糊集对特定边坡进行了分析；Li等［12］利用随机响应面法对岩石边坡进行了可靠性研究；庞小朝等［13］将协方差分解技术和谱代替法分别应用于蒙特卡罗随机有限元法，分析了边坡的局部失效概率。

本文通过一次二阶矩法（FORM）、蒙特卡罗模拟（MCS）和有限差分数值分析相结合的方法对强风化岩石边坡进行了可靠性分析，其中岩石边坡的岩土材料参数定义为二维（2D）空间变异参数，基于实验室或原位测量得到的数据，利用统计和概率理论建立，该参数的不确定性模型。利用乔里斯基分解的随机场理论定义2D空间变异的岩土参数，如凝聚力（c）、内摩擦角（φ）和重度（γ′），进而通过有限差分数值分析研究岩土参数变化和自相关距离对边坡安全系数和可靠性指标的影响。

2 可靠性分析模型

2．1 等效连续模型

岩体力学强度是由岩体的不连续程度、结构面数量和岩块强度共同决定。强风化岩石边坡是由许多不同岩体节理面切割形成的，边坡稳定性情况不能够由单一的岩块强度来决定，必须充分考虑节理因子、节理方向、节理间距、节理强度等参数对边坡稳定性的影响。为了考虑节理面对边坡的影响，将拟研究边坡等效为连续介质体，并采用基于经验公式得到的等效连续介质模型，获得高风化岩石边坡的特征参数。当从完整岩体中获得岩石裂隙特征时，即含有节理岩石的强度受以下的因素影响：①节理间距Jn；②节理方向，通常采用倾角α和节理倾向参数n进行表示；③节理强度γ。倾角α与节理倾向参数n的变化关系如表1所示，节理强度参数γ与完整岩体的单轴抗压强度σci变化关系如表2所示。

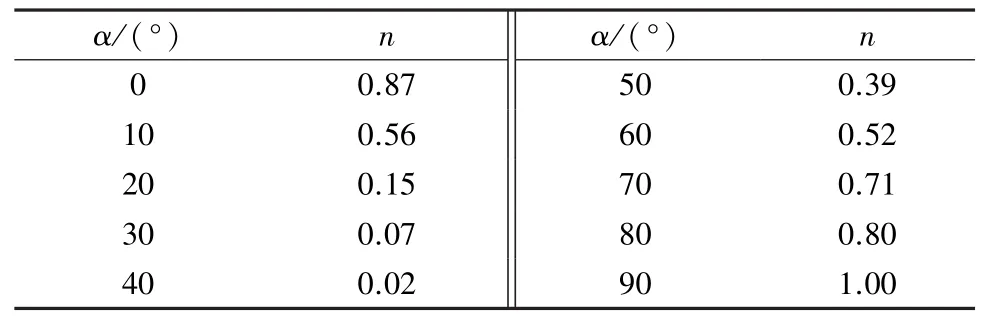
表1　倾角α与节理倾向参数n的变化关系Table 1 Variation of joint inclination parameter n with inclination angle α

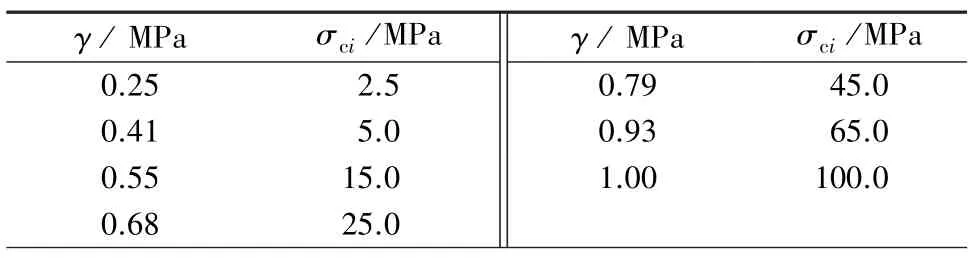
表2　γ与完整岩体单轴抗压强度σci的变化关系Table 2 Variation of γ with uniaxial compressive strength σciof intact rock

对于特定裂隙的岩体，其节理因子Jf为

式中Jf，Jn，n和γ分别表示节理因子、节理间距、节理倾向参数和节理强度。

当得知完整岩体的力学特性和节理因子时，裂隙岩体的力学特性就可以根据式（2）和式（3）的统计关系方程得到。

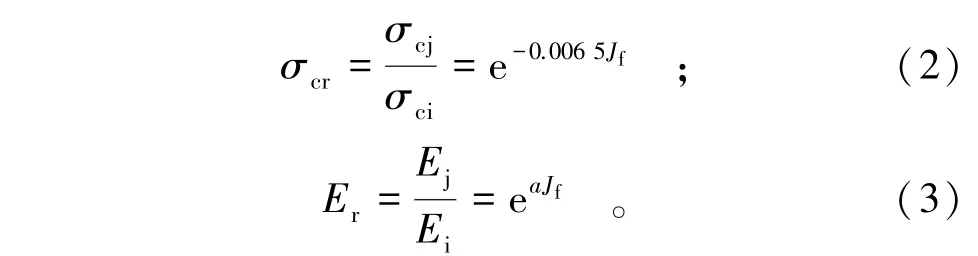
式中：σcr表示单轴抗压强度率；σcj表示裂隙岩体的单轴抗压强度；σci表示完整岩体的单轴抗压强度；Er表示切线模量率；Ej表示裂隙岩体的切线模量；Ei表示完整岩体的切线模量；σ3表示围压；a表示不同围围压下的经验常数，其取值如表3所示。

表3　不同围压下的a值Table 3 Values of empirical constant a under different confining pressures

在本文研究中，含有节理岩体的等效连续介质模型的特征参数取值如下：弹性模量（E）、凝聚力（c）、内摩擦角（φ）和重度（γ′）分别为5 GPa，58 kPa，30°和18 kN／m3，并假定服从摩尔－库伦破坏准则。

2．2 岩土材料参数的空间变异

岩土工程和地质工程最主要的特性是他们的工程参数不确定性和潜在不确定性带来的相关风险。岩土工程参数不确定性模型，需要利用统计和概率分析的方法对实验室或原位测量得到的数据进行定量评估建立。

在概率分析中，参数定义为概率密度函数的连续随机变量和分布函数的参数。在岩土工程实践中一般认为，岩土工程的参数或是服从均匀分布的变量，或是服从对数正态分布的连续随机变量，均匀分布和对数正态分布情况下的概率分布函数的参数直接与统计时的无偏估计相关，即测量数据集的样本均值（μ）和标准方差（σ）。协方差cov（即σ／μ），作为一个无量纲变量，可以有效评判比较数据样本集中与样本均值离散程度的大小，从而常被用来量化岩土工程的不确定性。当特定场地的数据不能提供估计随机变量参数时，其不确定性通过假设参数的协方差与其他地点相同量级来实现。表4为本文选定岩土参数的协方差变化范围。

表4　选定岩土参数协方差变化范围Table 4 Range of covariance variation of selected geotechnical parameters

众所周知，只有2个二阶矩统计数据，无论是在实验室测试或者现场测试，观测测量样本的均值（μ）和标准方差（σ）是不足以描述岩土工程特性的空间变异。这主要因为岩土工程特性在二维和三维空间是变化的，于是需要引入空间自相关参数。

空间自相关的定义是指一些变量在同一个分布区内的观测数据之间潜在的相互依赖性。空间变异模型参数中的自相关距离（γO），反映了岩土工程特性参数在空间范围内与其他位置参数依赖性的强弱，γO越大，表明岩土工程参数在空间范围内与其他位置参数的依赖性越强，反之亦然。

2．3 参数空间变异模型

近年来，随着计算机性能和随机场仿真算法效率的进一步提高，越来越多的研究人员逐渐开始利用随机有限元来分析和模拟材料特性空间变异。在随机有限元分析中，建立具有统计属性有限元方程，在每次蒙特卡罗模拟开始时将岩土参数作为多维数随机场，多次循环进行蒙特卡罗模拟。用均值（μ）、二维空间中的协方差（cov）和相关距离（δv）代表原位岩土工程参数的特性，最终得到用于设计的参数。例如，岩土工程特性参数（k）被视为空间随机变量并假设服从自相关对数正态分布，其参数均值为μk、标准方差为σk、相关性距离为δk。在一个随机场模型中，假设岩土工程特征参数服从对数正态分布，则一个对数正态分布的随机场可以表示为

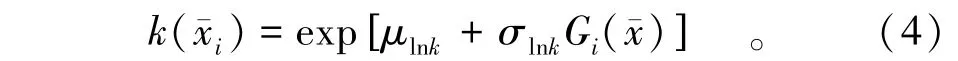
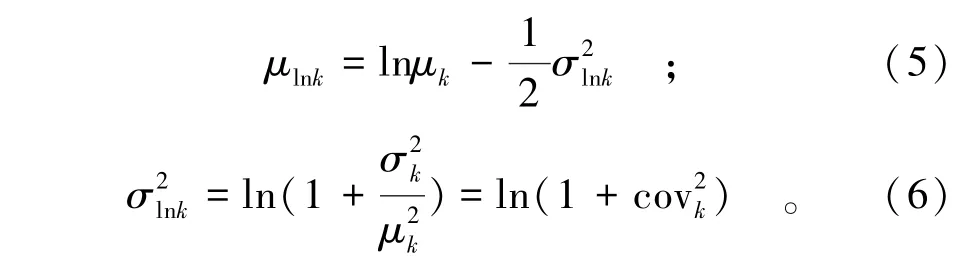
相关函数方程服从指数衰减，即

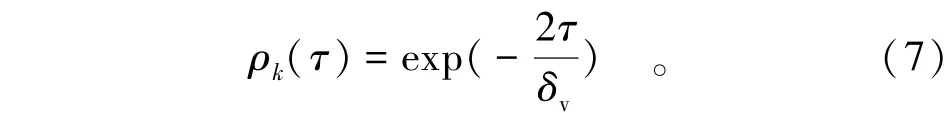
ρk＝L×LT。（8）

对于给定矩阵L，相关标准正态随机场为

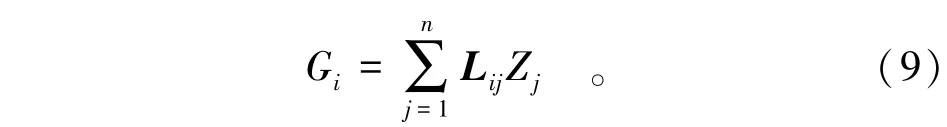
式中Zj表示服从独立标准正态分布的随机变量序列。

2．4 可靠性分析

如果通过定义需求值为D、能力值为C，对于相互独立均匀分布的C和D，则安全边际或性能函数G（x）或M可以定义为G（x）＝M＝C－D 。（10）

计算可靠性指标β为

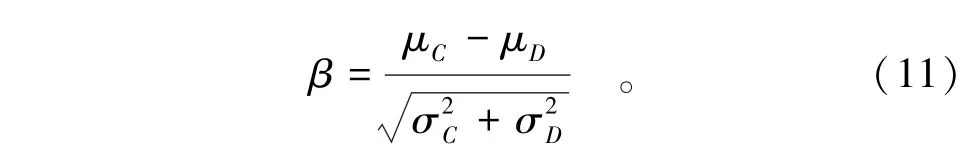
在相互独立对数正态分布的情况下，均匀分布C和D的性能函数G（x）可以定义为

G（x）＝M＝C／D 。（12）

则可靠性指标β可以进一步表示为

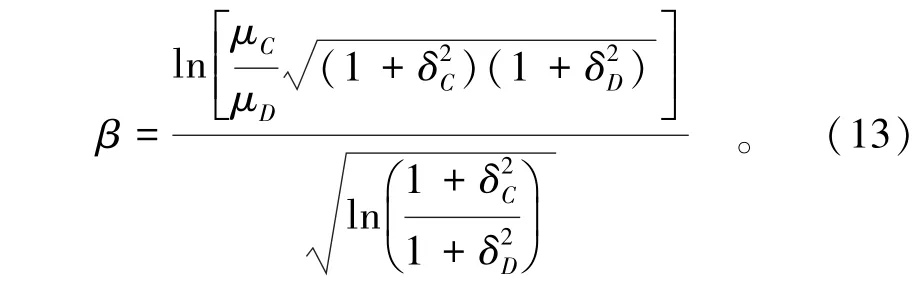
式中δC和δD分别代表C和D的协方差。美国陆军工程兵团（USACE）特别探讨了岩土工程和基础设施项目中的目标失效概率ρf和可靠性指标β，提出了可靠性指标的建议指导值。当可靠性指数β＞4．0时，则表示系统具有良好的性能；当可靠性指数β＞3．0时，则表示系统性能高于平均水平。

3 算例分析

对于一个强风化岩石边坡工程（高度为2．5 m，坡度角为30°），进行考虑岩土工程参数空间变异的可靠性分析，在参数分析研究中，考虑岩土工程参数，如凝聚力、内摩擦角和重度的空间变异性，协方差典型值认为在5%～30%之间和自相关距离典型值认为在0～15 m范围内，凝聚力参数呈现线性变化，其中顶部的c＝20 kPa，这个假定实现了在原位条件下考虑了上覆岩层的影响以及岩体风化崩解的程度。假设岩土工程参数具有各向同性自相关结构，即相关距离在水平方向和垂直方向均相同。

为了在有限差分数值工具中实现空间模型，首先从式（6）中生成相关矩阵。滞后距离（τ）值大小由连续网络里面两地中心的距离决定。如图1所示，选取网格的数量为20×20，网格节点1和2之间的中心距离为dx，则这2个网格节点之间的相关关系可以通过将计算值τ＝dx代入式（7）中建立。同样，网格节点1和节点3、节点4、节点5之间的相关关系可以通过将τ＝2 dx，τ＝3 dx和τ＝4 dx代入式（7）中建立，同时节点1和节点21、节点22和节点23的中心距离分别为：dy，。因此，相关矩阵的第1行值分别是网格节点1和其他网格节点的相关系数，则相关系数矩阵第1行具有连续的400个数值。因此，考虑到所有网格节点，相关矩阵的大小是400×400。一旦建立了这样的相关矩阵后，通过使用柯列斯基分解方法分解其为上三角矩阵和下三角矩阵的矢量积。通过生成一个独立标准正态随机变量序列（均值μ和标准方差σ均为0）和利用分解式（8）中的相关矩阵获得相关标准正态随机场；然后利用式（9）得到相关标准正态随机场；最后利用k的均值、标准差和式（3）得到不同网格节点位置服从对数正态分布的岩土参数特性。最后，通过数值模拟实现了所有岩土工程参数二维空间的变化。图2为经过上述步骤分析得到的凝聚力参数的分布图。由图2的统计结果可知，边坡顶部处μo＝20 kPa和均值μ ＝58 kPa，协方差cov＝20%，相关距离δv＝1．0 m，顶部往下至底部的μ变大且呈现非线性，符合风化岩石边坡的实际情况。

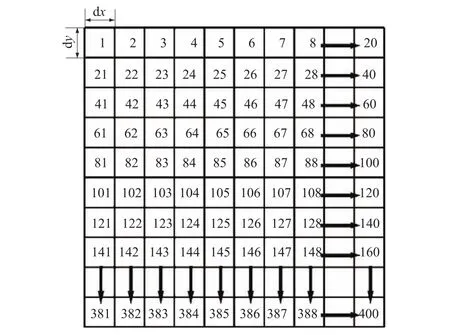
图1　基于随机场模型有限差分网格的离散化Fig．1 Discretization of finite difference grid in the random field modeling

图2　二维空间中凝聚力参数的分布Fig．2 Distribution of cohesion parameter in 2D space

值得注意的是，每一次产生的凝聚力参数都不同，这是因为每一次都是随机产生，因此蒙特卡罗模拟（MCS）均执行关于输出响应的平均值和标准差等统计信息，如安全系数。对强风化岩石边坡进行可靠性分析，其能力值（C）是边坡的计算安全系数（FS），而其需求值（D）则统一取值为1．0。对于每个输入岩土参数的实现，给定岩石边坡的安全系数是由调用内置的强度折减法实现。图3是当自相关距离为10 m时，运算到900步时的计算示意图；表5是自相关距离为10 m时，不同协方差下的安全系数。由表5可见，随着协方差逐渐变大，强风化岩石边坡的安全系数逐渐减小。

应该指出的是，在估计均值和方差的输出响应中达到设置可接受误差为5．0%，显著性水平＝0．05 （95%置信水平）至少需要进行1 536次蒙特卡罗模拟。目前的分析，是通过对岩石边坡的安全系数进行3 000次蒙特卡罗模拟完成对统计参数的估算，即均值（μ）和标准方差（σ）。假设安全系数FS服从对数正态分布，利用式（13）即可对估算值进行二阶矩法的可靠性分析。

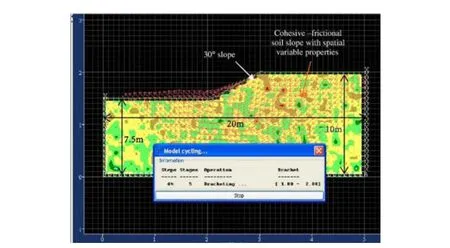
图3　自相关距离为10 m时计算示意图Fig．3 Calculation figure when the autocorrelation distance is 10m

表5　自相关距离为10 m时不同协方差下的安全系数Table 5 Safety factors corresponding to different covariance when the autocorrelation distance is 10m

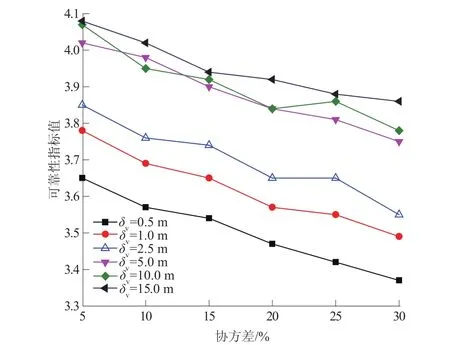
图4　协方差和相关距离对可靠性指标的影响Fig．4 Influences of covariance and correlation distance on the reliability index

图4为强风化岩石边坡可靠性评估时，协方差（cov）和相关距离（δv）对可靠性指标值（β）的影响。由图4可以看出，β随着岩土工程参数的协方差的增大而减少，而随着相关距离的增加而增大，同时也可见，相关距离为10 m的曲线上某些值比相关距离为5 m曲线上的值低。这些轻微差异不仅是由蒙特卡罗模拟中有限参数数量引起，而且还是由岩土工程参数空间变异数值模型的固有随机性引起的。弱相关性与那些具有强相关性相比，其更能真实地表征岩土工程特性的不稳定性；且在蒙特卡罗模拟过程中，评估安全系数时得到的变异系数更大。因此，我们可以得出，可靠性指标随着自相关距离值增加而增大。

综上所述，岩土工程参数的空间变异性对高风化岩石边坡的稳定性评价结果有着显著的影响；同时参数的调查研究也表明，这种边坡的真实稳定性评价无法通过传统安全系数方法获得。

4 结 论

本文研究通过建立强风化岩石边坡模型，将强风化岩石边坡等效为连续介质模型，岩石参数采用空间变异模型表示，对其进行概率范畴下的蒙特卡罗模拟循环，并进行了安全性评价。最后通过分析强风化岩石边坡的稳定性，得到如下结论：

（1）强风化岩石边坡的安全性评价不能通过单一参数值分析其稳定性，因为其上覆岩层的影响及岩体的风化崩解程度导致其风化程度不一和随机性较大，只有通过地质调查确定岩石参数的均值、方差和协方差，从而建立岩石参数空间变异模型，这样才能得到真实的边坡安全性评价。

（2）通过对不同岩石参数的协方差的可靠性分析研究，可以得知随着岩石边坡参数协方差值的增大，强风化岩石边坡的可靠性指标值逐渐减小。

（3）通过对不同岩石参数自相关距离的可靠性分析研究，可以得知随着岩石边坡参数的自相关距离的增大，强风化岩石边坡的可靠性指标值逐渐增大。

（4）经过对不同岩石参数的协方差分析计算，得到强风化岩石边坡的安全系数值随着参数的协方差的增大而减小。

显然，岩土工程参数空间变异对特定岩石边坡的稳定性评价具有很大的影响，因此应在边坡常规分析和设计过程考虑岩土工程参数的空间变异对岩石边坡的影响。

参考文献：

［1］ 谭晓慧．边坡稳定分析的模糊概率法［J］．合肥工业大学学报（自然科学版），2001，24（3）：442－446．

［2］ 杨建贵，蔡 新，张永乐．边坡稳定的模糊随机可靠性分析［J］．河海大学学报（自然科学版），2002，（1）：58－62．

［3］ 王 宇，贾志刚，李 晓，等．边坡模糊随机可靠性分析的模糊点估计法［J］．岩土力学，2012，33（6）：1795－1800．

［4］ 杨 坤，周创兵，张 昕，等．边坡块状结构岩体模糊随机可靠性分析［J］．岩石力学与工程学报，2006，25（2）：407－413．

［5］ 王亚军．基于模糊随机理论的广义可靠度在边坡稳定性分析中的应用［J］．岩土工程技术，2004，18（5）：217－223．

［6］ 蒋建群，徐 辉．边坡稳定模糊随机可靠度评价及其应用［J］．水力发电学报，2006，25（4）：126－130．

［7］ 贾厚华，贺怀建．边坡稳定模糊随机可靠度分析［J］．岩土力学，2003，24（4）：657－660．

［8］ 付士根．基于模糊随机可靠性的边坡稳定性评价［J］．中国安全生产科学技术，2012，8（8）：98－101．

［9］ 陆黎斌，陈璞磊．基于模糊随机理论的边坡可靠度分析［J］．低温建筑技术，2014，36（1）：140－142．

［10］DODAGOUDAR G R，VENKATACHALAM G．Reliabili⁃ty Analysis of Slopes Using Fuzzy Sets Theory［J］．Com⁃puters and Geotechnics，2000，27（2）：101－115．

［11］GIASI C I，MASI P，CHERUBINI C．Probabilistic and Fuzzy Reliability Analysis of a Sample Slope near Aliano ［J］．Engineering Geology，2003，67（3）：391－402．

［12］LI D，CHEN Y，LU W，et al．Stochastic Response Sur⁃face Method for Reliability Analysis of Rock Slopes Invol⁃ving Correlated Non⁃normal Variables［J］．Computers and Geotechnics，2011，38（1）：58－68．

［13］庞小朝，周小文，温庆博，等．随机场的模拟及其在堤坡可靠性分析中的应用［J］．长江科学学院院报，2002，19（4）：27－29．

（编辑：姜小兰）

Application of Reliability Analysis Theory to Stability Analysis of Highly Weathered Rock Slope

XU Gen⁃hong
（College of Urban Construction，Zhejiang Shuren University，Hangzhou 310015，China）

Abstract：Reliability analysis on highly weathered rock slope stability is carried out by means of a combination of first order two moment，Monte⁃Carlo simulation and finite difference numerical analysis．Firstly，the rock slope is treated as a continuous medium，and the characteristic parameters of the highly weathered rock slope are obtained by using equivalent continuum model．Subsequently，the material parameters of rock slope are defined as two⁃di⁃mensional variable parameters，and the uncertainty model of the variable parameters is established by employing the

first order two moments method．Then the spatial variability of geotechnical parameters is simulated by Monte⁃Carlo method．Finally，the influence of covariance and autocorrelation distance on safety factor and reliability index is re⁃searched by using finite difference method．Results show that the spatial variability of the geotechnical parameters has great influence on the evaluation of specific rock slope stability．The safety assessment for highly weathered rock slope could not be determined by single parameter．As covariance of rock slope parameter increases，the reliability index and safety factor reduce gradually；and with the increase of autocorrelation distance，reliability index increa⁃ses gradually．Therefore，the effects of spatial variability of geotechnical parameters of rock slope should be consid⁃ered in conventional slope analysis and design process．

Key words：rock slope；reliability analysis；highly weathered；spatial variation characteristics；stability

作者简介：徐根洪（1960－），男，浙江建德市人，讲师，实验师，主要从事岩土工程测试、土工试验和边坡研究，（电话）13858129053（电子信箱）genhongxu＠163．com。

收稿日期：2014－11－19；修改日期：2014－12－25

中图分类号：TV22

文献标志码：A

文章编号：1001－5485（2016）03－0065－05