塑性混凝土相对弹性变形特性试验研究

宋 力，刘璐璐，高玉琴

（1．黄河水利委员会黄河水利科学研究院，郑州 450003；2．华北水利水电大学土木与交通学院，郑州 450011）



塑性混凝土相对弹性变形特性试验研究

宋 力1，刘璐璐2，高玉琴1

（1．黄河水利委员会黄河水利科学研究院，郑州 450003；2．华北水利水电大学土木与交通学院，郑州 450011）

摘 要：为了探讨塑性混凝土应力－应变曲线直线段P1和P2的取值范围，从而得出弹性模量的取值，通过对4组不同混凝土配合比的48个试件，进行了单轴抗压强度试验。通过试验绘制了典型应力－应变曲线，选取了曲线的近似直线段，进而分析割线模量和计算区间内切线模量均值的相近程度，并对直线段弹性模量计算公式中如何对P1和P2取值进行了研究。试验结果表明：塑性混凝土应力－应变曲线上升段存在近似直线段；塑性混凝土的强度＜5MPa时，选取60%和80%峰值应力作为弹性模量计算公式中P1和P2的值比较符合塑性混凝土的实际情况；反之，则需要更进一步的研究。试验研究成果为解决低强度塑性混凝土材料性能取值难问题提供了一种较好的方法。

关键词：塑性混凝土；应力－应变曲线；割线模量；切线模量；P1和P2取值点

1 研究背景

塑性混凝土是一种具有一定抗渗能力、低强度、低弹性模量和大应变特点的特殊混凝土［1］。因塑性混凝土的弹性模量与土体的弹性模量相差不大的特点，近年来在土石坝和围堰防渗工程中的应用日益增多，并成为了水利水电工程覆盖层防渗处理的首选材料［2－3］。弹性模量是衡量塑性混凝土性能的重要特性指标之一，由于塑性混凝土的弹性模量计算没有现行的规范，国内学者［4－6］均是借鉴《水工试验规程》［7］普通混凝土弹性模量计算公式计算的，但塑性混凝土的强度比较低，用普通混凝土弹性模量的计算公式计算出的结果并不符合实际。

本文根据塑性混凝土的自身特性，以4组配合比下共48个试件的单轴抗压试验为基础，通过探讨塑性混凝土应力－应变曲线直线段P1和P2的取值范围，得出弹性模量的取值方法。

2 试验设计及结果

2．1 试验材料及配合比

塑性混凝土试件制作采用河南孟电生产的P·O32．5号普通硅酸盐水泥；细骨料为河砂，级配曲线位于Ⅱ区，属于中砂；粗骨料为粒径5～20 mm的连续级配的碎石；水为普通自来水；膨润土为四川乐山生产的钠质膨润土。根据试验目的，共设计了4组配合比，每组仅考虑28 d龄期，见表1。每个配合比分别制作6个150 mm×150 mm×300 mm棱柱体试件和6个Φ150 mm×300 mm的圆柱体试件。塑性混凝土试件浇筑成型后静置48 h后拆模，并移至标准养护室养护至28d龄期后按照《水工混凝土试验规程》（SL 352—2006）［7］进行相关试验。

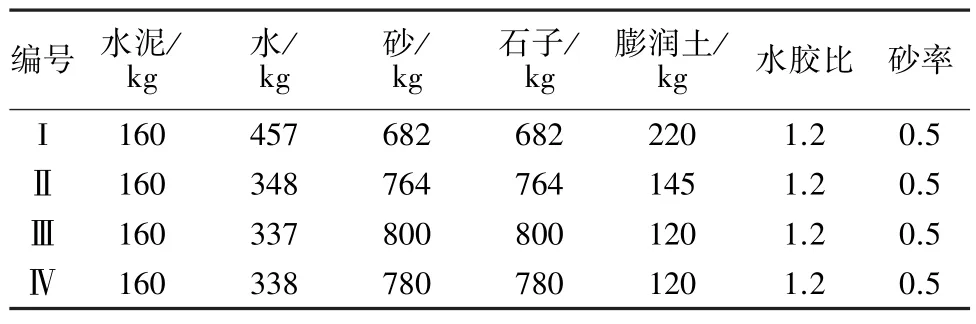
表1　塑性混凝土的配合比Table 1 Mix proportion of plastic concrete

试验采用CMT5105的电子万能试验机，采用位移控制，加载速度为0．2mm／min。轴向荷载和试件的变形均由自动传感器采集，并将采集到的数据自动输入计算机内绘制成应力－应变曲线。考虑到塑性混凝土抗压强度低变形大特点，采用应变片法很难反映出塑性混凝土的应变，并且为了试验仪器装置的方便使用，根据文献［4］建议，采用全标距法开展试验。

2．2 试验结果

图1是典型的应力－应变曲线。4组配合比下各组试件峰值抗压强度、峰值应变的试验结果见表2。表2中，以3个试件测定值的算术平均值作为该组试件的抗压强度值。当3个测定值中的最大或最小值有一个与中间值的差值超出中间值的15%时，则把最大及最小值一并舍去，取中间值作为该组试件的试验值。

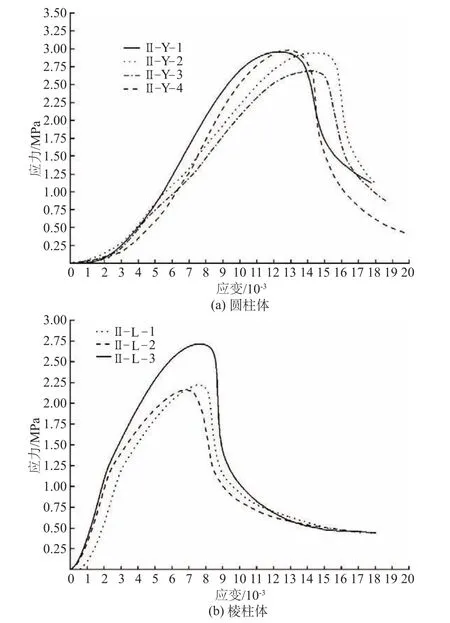
图1　圆柱体和棱柱体典型应力－应变曲线Fig．1 Typical stress⁃strain curves of cylinder and prism specimens

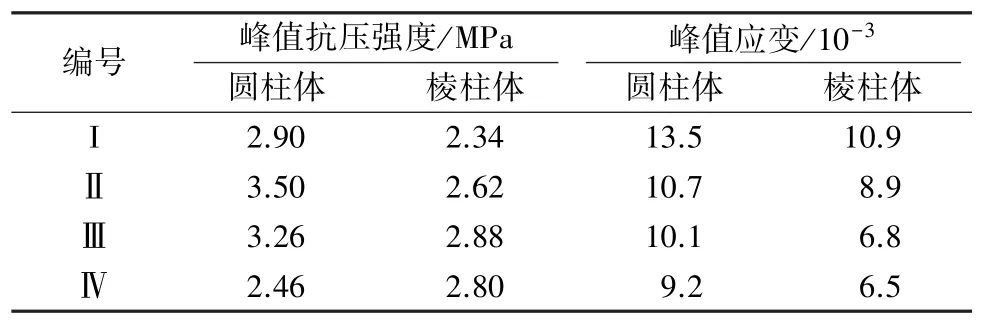
表2　试件基本力学指标试验结果Table 2 Test results of basic mechanical properties of specimens

3 P1和P2的选取

文献［8］指出塑性混凝土应力－应变曲线的整个变化过程可以分为4个阶段（图2），第2个阶段为拐点A处到峰值应力B处，应力增长幅度大于应变增长幅度，曲线呈现凸特征，曲线在AB段的性质，与常规混凝土弹性阶段的应力－应变曲线较为接近，基本呈现线性变化，A和B两点之间即为弹性模量计算公式中P1和P2取值区域。

图2　应力－应变典型曲线的分段性Fig．2 Four segments of typical stress⁃strain curve

根据应力－应变曲线上相邻2点应力变化量与应变变化量的比值求取此处的切线斜率，即切线弹性模量Et为

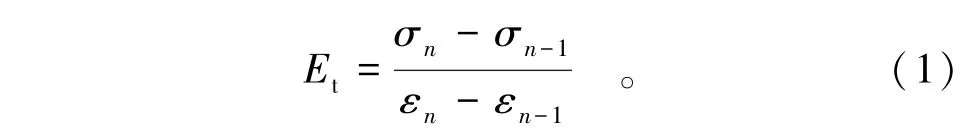
式中：Et为切线弹性模量（MPa）；σn和σn－1为相邻2点的应力值（MPa）；εn和εn－1为相应相邻2点的应变值。根据式（1）计算出切线模量并绘制切线弹性模量Et与应力σ的关系曲线，选取曲线AB段之间Et变化范围较小且近似直线的应力区间。计算40%～60%，40%～70%，40%～80%，50%～70%，50%～80%，60%～80%峰值应力的割线模量与对应范围内切线弹性模量Et的均值的比值，割线模量与切线模量均值的比值最接近1的即为塑性混凝土弹性模量P1和P2的取值点。以圆柱体试件为例，图3是切线弹性模量Et与应力σ的关系曲线图。

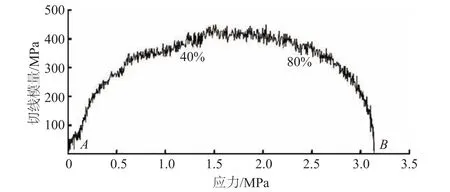
图3　切线弹性模量与应力的关系Fig．3 Relationship between tangent modulus and stress

由图3可知，AB段40%～80%的峰值应力间的切线模量比较接近直线，与普通混凝土应力－应变曲线的弹性段相似，故P1和P2的取值点要在40%～80%区间内寻找。然后计算出40%～60%，40%～70%，40%～80%，50%～70%，50%～80%及60%～80%峰值应力的割线模量与对应范围内切线弹性模量的均值的比值见表3。

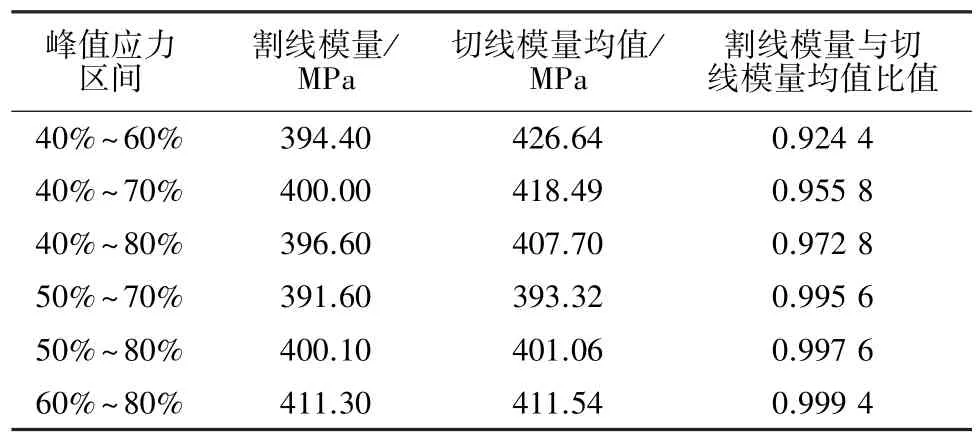
表3　峰值应力各区间下割线模量与切线模量均值及比值Table 3 Ratios of secant modulus to mean tangent modulus under different ranges of peak stress

从表3中我们可以得出50%～70%，50%～80%，60%～80%这3个区间割线模量与切线模量均值的比值更接近于1。为了更加准确地得出P1和P2，我们通过对所有试件的结果进行上述处理，结果见表4。表4是4组配合比下12个圆柱体和12个棱柱体试件峰值应力40%～80%割线模量与对应取值范围切线模量均值的比值，割线模量与切线模量均值比值最接近1的区间所占比例为：50%～70%峰值应力区间，所占百分比为25%；60%～80%峰值应力区间，所占百分比为75%。另外，图4也表明了60%～80%区间内切线模量数据与割线模量拟合较好。通过统计分析，我们可以在计算过程中选取60%和80%峰值应力对应点作为弹性模量计算公式中P1和P2的取值点。

表4　各计算区间割线模量与切线模量均值比值Table 4 Ratios of secant modulus to mean tangent modulus in different calculation intervals

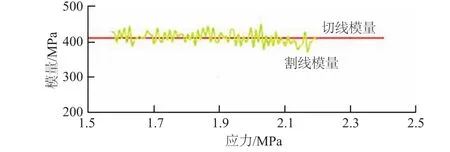
图4　60%～80%峰值应力区间割线模量与切线模量均值比较Fig．4 Comparison of secant modulus and mean tangent modulus in the range of 60%～80%peak stress

4 结 论

本文通过塑性混凝土单轴抗压相对弹性阶段定义的试验研究，分析了应力－应变曲线的特征以及割线模量和计算区间内切线模量均值的相近程度，得出以下结论：

（1）根据塑性混凝土试件受压破坏试验绘制出的应力－应变曲线中存在一个斜率相对稳定的阶段，见图2的AB段。

（2）当塑性混凝土的强度＜5 MPa时，选取60%，80%峰值应力作为弹性模量计算公式中P1，P2的值比较符合塑性混凝土的实际情况，可较好地反映塑性混凝土弹性模量的特征；当塑性混凝土的强度＞5MPa时，公式中P1，P2的取值则需要更进一步的研究。

参考文献：

［1］ 袁 枚，赵家声．防渗墙塑性混凝土弹性模量试验方法的研究［J］．水利水电施工，2011（3）：63－66．

［2］ 蒋凯乐，李云鹏，张如满，等．塑性混凝土防渗墙土反力系数反演［J］．岩土力学，2012，33（2）：389－394．

［3］ 李青云，张建红，包承纲．风化花岗岩开挖弃料配制三峡二期围堰防渗墙材料［J］．水利学报，2004，（11）：114－118．

［4］ 高丹盈，赵利梅．塑性混凝土弹性模量的计算方法［J］．郑州大学学报（工学版），2009，30（4）：15－17．

［5］ 王四巍，于怀昌，高丹盈．塑性混凝土弹性模量室内试验研究［J］．水文地质工程地质，2011，38（3）：73－75．

［6］ 杨 林，杨 静，姬宏奎．塑性混凝土弹性模量研究［J］．三峡大学学报（自然科学版），2012，34（5）：66－68．

［7］ SL352—2006，水工混凝土试验规程［S］．北京：中国水利水电出版社，2006．

［8］ 宋 力，常芳芳．塑性混凝土应力－应变特性的试验研究［J］．南水北调与水利科技，2014，12（2）：67－70．

（编辑：姜小兰）

Experimental Study on the Relative Elastic Deformation of Plastic Concrete with Low Strength

SONG Li1，LIU Lu⁃lu2，GAO Yu⁃qin1
（1．Yellow River Institute of Hydraulic Research，Yellow River Conservancy Commission of the Ministry of Water Resources，Zhengzhou 450003，China；2．School of Civil Engineering and Communication，North China University of Water Resources and Electric Power，Zhengzhou 450011，China）

Abstract：In order to determine two endpoints（P1and P2）in the straight⁃line segment of stress⁃strain curve of plastic concrete，and to obtain the elastic modulus，we carried out uniaxial compression test on 48 concrete speci⁃mens of four different mix proportions．Through analyzing typical stress⁃strain curve，we selected approximated straight⁃line in the curve，and compared the secant modulus with mean value of tangent modulus．On this basis，we studied how to determine P1and P2．The results show that 1）the approximated straight⁃line segment appears at the ascent stage in the stress⁃strain curve of plastic concrete；2）with given strength of plastic concrete less than 5 MPa，it is suitable to choose 60%and 80%of peak stress as the elastic modulus of P1and P2，respectively，other⁃wise，further study is required．Finally，the research offers a method for determining the values of material perform⁃ance of plastic concrete with low strength．

Key words：plastic concrete；stress⁃strain curve；secant modulus；tangent modulus；position of P1and P2in stress⁃strain curve

通讯作者：刘璐璐（1990－），男，河南南阳人，硕士研究生，研究方向为工程结构设计与防减灾技术，（电话）15238302182（电子信箱）tiankong⁃chumo＠163．com。

作者简介：宋 力（1979－），男，河南南阳人，高级工程师，硕士，主要从事混凝土结构试验、数值仿真模拟等研究，（电话）13937176870（电子信箱）songli＠yeah．net。

基金项目：中央级公益性科研院所基本科研业务费专项（HKY－JBYW－2013－10）；水利部堤防安全与病害防治工程技术研究中心开放课题基金项目（201501）

收稿日期：2014－12－23；修回日期：2015－01－11

中图分类号：TV331

文献标志码：A

文章编号：1001－5485（2016）03－0147－04