非线性水轮机调节系统稳定性分析
唐兆祥,张德虎,刘志淼(河海大学能源与电气学院,南京 211100)
0 引 言
水轮机调节系统是集水力、机械、电气为一体的综合型控制系统,调节对象为复杂的非线性非最小相位系统[1]。水轮机调节系统的安全稳定地运行对水力发电机组的安全经济运行有着直接地影响,水轮机调节系统的调节品质对电网系统的安全运行和供电品质也有重要影响。因此,深入研究水轮机调节系统显得尤为重要,非线性水轮机调节系统的动力学过程也已成为水利水电工程的研究热点之一。
由于线性控制理论无法适应系统运行点的大范围变化,近几年来非线性控制理论被引入到水轮机调节系统的研究中。Luz Alexandra曾指出基于非线性水轮机模型的调节系统是研究水力系统与电力系统相互作用的最精确的模型[2]。在非线性水轮机调节系统的研究成果中,基于微分几何的反馈线性化方法及基于反馈线性化的非线性鲁棒控制方法居于主流地位,取得较好结果。此外,水轮机调节系统的混沌现象分析[3]、Hopf分岔分析[4,5]、模糊控制及神经网络等控制理论的研究为水轮机调节系统的控制器设计提供了新的方法。本文在对非线性水轮机调节系统分析的基础上,运用非线性动力系统线性化的方法对系统进行分析,为非线性调节系统的参数整定及稳定运行提供理论依据。
1 非线性水轮机调节系统建模
本文采用1992年IEEE提出的单机单管无调压室的非线性水轮机模型,如图1所示[6]。图中G为导叶开度相对值;qnl为空载相对流量;q′t为水轮机过流流量相对值;h′t为水轮机进口处水头相对值;f为水头损失系数;D为转速偏差阻尼系数;At为水轮机出力增益系数。

图1 非线性水轮机模型Fig.1 Non-linear Model of Hydro-turbine
假设水为不可压缩流体,引水管道为刚体,则有压引水系统发生水击时为刚性水击,有压引水系统的动力学方程为:
(1)
采用相对值形式表示为:
(2)
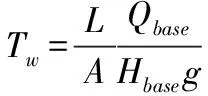
设各变量的相对值与偏差相对值之间有如下关系:
(5)
式中:nr、Qr、ar分别表示水轮机额定工况下的转速、流量、导叶开度。
本文采用一阶发电机模型,其方程为:
(6)
式中:Ta为水轮机惯性时间常数;Pm、mg分别为水轮机出力和发电机阻力矩。
本文的调速器模型采用目前实际应用中较为广泛的PID型调速器,如图2所示。
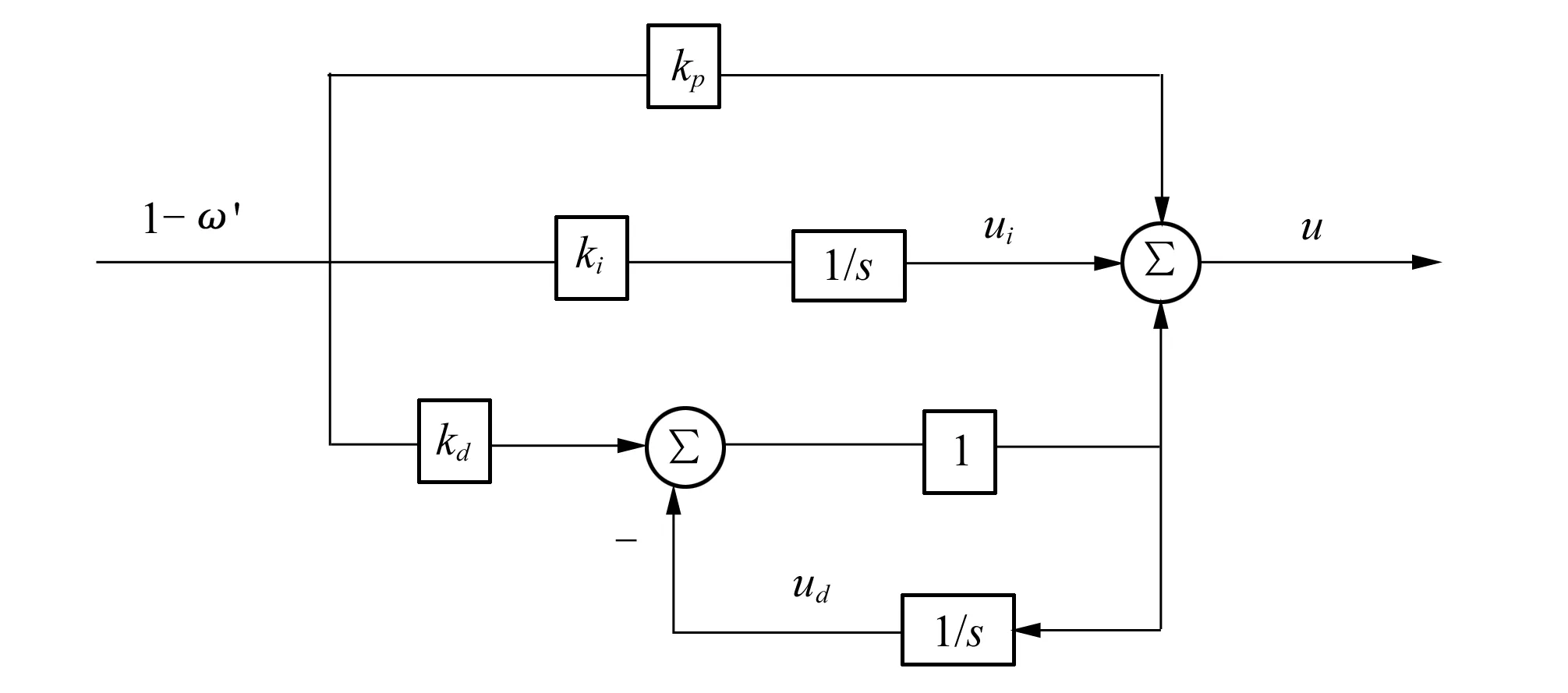
图2 PID调速器Fig.2 PID Governor
调速器的时域方程为:
u=kp(1-ω′)+ui+kd(1-ω′)-ud
(7)
式中:u为调速器的输出;ω′为转速相对值。
液压随动系统的动态特性方程:
(8)
结合式(1)~式(8)和非线性水轮机模型图,可得到非线性水轮机调节系统模型为:
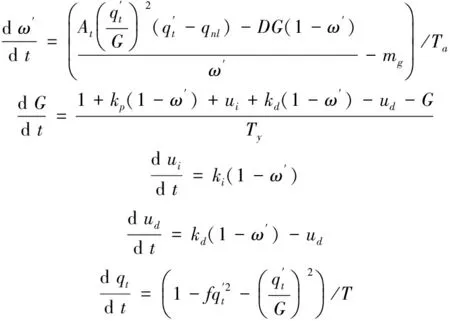
(9)
2 非线性调节系统的稳定性分析
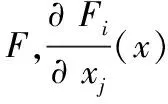
水轮机调节系统的各参数取自文献[6],Qr=71.43 m3/s,QNL=4.3 m3/s,Hr=138.9 m,A=15.2 m2,L=465 m,Ta=5.4,Ty=0.2,f=0.01,D=0.5,本文仅分析当ki、kd固定时,系统稳定时kp的取值范围,此处取ki=0.2、kd=0.2。
可以看出,系统模型是一个C∞系统,则当不动点特征根都具有负实部时,系统不动点是一个双曲不动点。此时线性化系统不动点与非线性系统不动点具有相同的稳定类型。式(9)的偏导数矩阵为:
(10)
矩阵J的特征多项式为:
λ5+7.35λ4+(12.86-1.85kp)λ3+(7.33-0.637kp)λ2+
(1.21kp+0.456)λ+0.242
下面将根据Hurwitz 判据对特征方程(10)式进行稳定性判断,式(10)的Hurwitz 矩阵为:
(11)
根据Hurwitz 判据,只要保证矩阵H行列式的各阶主子式均大于零,则线性化系统的特征根都具有负实部。各阶主子式如下:
H1=7.35>0
(12)
H2=87.19-12.96kp>0
(13)
H3=8.3k2p-216kp+616>0
(14)
H4=10k3p-263k2p+729kp+10.4>0
(15)
H5=2.4k3p-63.7k2p+176kp+2.52>0
(16)
综合(10)式,可得:
-0.01 (17) 即-0.01 从线性控制理论可知,控制器参数从稳定域中心向边界运动时,系统由强稳定状态向弱稳定状态转变,在边界处,系统处于临界稳定状态。这同样可以从Lyapunov稳定理论得到证明。图3为最大Lyapunov指数随kp的变化曲线。Lyapunov稳定理论指出:仅当系统最大Lyapunov指数为零,其他均为负时,系统处于临界稳定状态。图3中-0.014 图3 Lyapunov指数图Fig.3 Lyapunov exponent of kp 当kp=-0.014时,系统转速变化、压力管道的流量变化和系统的三维相图如图4所示。从图4可以看出,流量和转速呈等幅周期变化,由于控制器比例环节的作用很小,系统流量的振荡幅值比扰动幅值要小,不足5%。从相空间可以看出,相轨迹将在一段时间后进入一个极限环。 图4 10%流量扰动,kp=-0.014时,机组转速、引水管道流量时域图及相轨迹图Fig.4 Time waveforms of speed and flow in penstock, phase trajectory response for q=1.1 with kp=-0.014 图5 10%流量扰动,kp=3.155时,机组转速、引水管道流量时域图及相轨迹图Fig.5 Time waveforms of speed and flow in penstock,phase trajectory response for q=1.1 with kp=3.155 当kp=3.155时,系统转速变化、压力管道的流量变化和系统的三维相图如图5所示。从图5可以看出,流量和转速呈等幅周期变化,由于控制器比例环节的作用较强,系统的振荡幅值比扰动幅值要大,达到15%。对比图4可以看出,随着比例作用的增强,各变量的振荡频率显著增加。这是由于较大的比例系数导致控制器对误差的响应较敏感。从相空间可以看出,相轨迹将在一段时间后进入一个极限环,且该极限环比图4的极限环要大。 图6是kp=1.25时,非线性系统的时域图和相图。从相图可以看出,此时系统不动点是一个强稳定型焦点,相轨迹会在短时间内进入不动点的一个小邻域范围内。反映在时域图上,可以看到流量和转速能够快速收敛到不动点。 水轮机调节系统是一个复杂的非线性系统。本文考虑了水轮机的非线性特性,建立了水轮机调节系统的非线性模型。在此基础上,运用非线性动力系统线性化的方法对系统进行分析,计算得到控制器参数的稳定域,且该方法有较高的精度。从仿真结果的分析可以看出,当控制器参数向稳定域边界运动时,系统稳定性开始恶化,且系统调节过程的振荡次数增加,随后会进入等幅振荡状态,最终将出现失稳现象。此外,还可以看到,线性化系统与非线性系统间存在一定 图6 10%流量扰动,kp=1.25时,机组转速、引水管道流量时域图及相轨迹图Fig.6 Time waveforms of speed and flow in penstock,phase trajectory response for q=1.1 with kp=1.25 的误差,但线性化系统的稳定域一定能使非线性系统稳定,且线性化系统的稳定域一定包含了使非线性系统强稳定的控制器参数。 □ [1] 凌代俭,陶 阳,沈祖诒.考虑弹性水击效应时水轮机调节系统的Hopf分岔分析 [J].振动工程学报,2007,20(4):374-379. [2] Tenorio Luz Alexandra lucero. Hydro Turbine and Governing Modeling[D]. Trodhein:University of Science and Technology,2010. [3] 陈帝尹,杨朋超,马孝义,等.水轮机调节系统的混沌现象分析及控制 [J].中国电机工程学报,2011,31(14):113-120. [4] 凌代俭.水轮机调节系统分岔与混沌特性的研究[D].南京:河海大学,2007. [5] 凌代俭,沈祖诒.水轮机调节系统的非线性模型、PID控制及其Hopf分岔[J].中国电机工程学报,2005,25(10):97-102. [6] Working group on prime mover and energy supply models for system dynamic performance studies. Hydraulic turbine and turbine control model for system dynamic studies [J]. Tansactions on Power System, 1992, 7(1):167-179. [7] 韩茂安,邢业朋,毕 平.动力系统导论[M].北京:机械工业出版社,2007:117-118. [8] 袁 璞,把多铎,宋 亮. 考虑限幅环节的水轮机调节系统建模与分析 [J].人民长江,2014,45(1):82-86. [9] 陈帝尹,郑 栋,马孝义,等.混流式水轮机调节系统建模与非线性动力学分析 [J].中国电机工程学报,2012,32(32):116-123.3 非线性系统仿真
4 结 语