基于Kalman-ARIMA模型的大坝变形预测

薛 洋，杨 光，许 雷(.河海大学水利水电学院，南京 20098；2.河海大学水文水资源与水利工程科学国家重点实验室，南京 20098)

变形是水工建筑物运行状态的重要效应量，也是最主要的监测量[1,2]，变形能够直观可靠地反映大坝的结构性态和安全状况[3]，因此，变形预测是大坝安全监测系统的关键组成部分，也是防汛调度的关键，对及时掌握大坝变形状态、确保大坝安全运行具有十分重要的作用[4,5]。在坝工实际问题中，影响大坝变形的因素极为复杂，除库水压力(水位)外，还有温度、降雨、渗流、施工、地基、周围环境和时效等[1,2]多种非线性因素，从而使得准确有效地对大坝变形进行预测具有一定的难度。目前，常用的大坝变形预测方法有多元线性回归分析法、有限元方法、灰色GM模型、模糊聚类分析法、遗传算法和时间序列分析法等。其中，基于三大经典监控模型(统计模型、确定性模型及混合模型)的变形预报与评价应用得最为广泛，但其存在参数确定困难、所建数学模型较为复杂、要求线性方程组非奇异与无病态且与大坝实际变形状况相吻合[6]等缺点，难以满足大坝变形预测的精度要求。

大坝变形监测数据序列一般呈现出显著的非平稳性和周期性，并且在监测过程中，易受自动化监测资料噪声污染。为提高大坝变形预测精度，及时准确地反映大坝变形状态，本文提出Kalman-ARIMA模型，即先利用卡尔曼滤波法对变形监测数据序列进行降噪处理，剔除随机干扰噪声(包括干扰噪声和动态噪声)，使得监测数据能够更准确地反映大坝变形的实际状况，然后利用自回归差分滑动平均混合模型(ARIMA模型)对滤波后的数据进行大坝变形预测，从而达到提高能大坝变形预测精度的目的。

1 卡尔曼滤波法

卡尔曼滤波是一种从与被提取信号有关的观测量中通过算法估计出所需信号的滤波算法[7,8]。目前，该方法广泛应用于动态数据处理过程中，它具有最小无偏差性，并且能够最大限度地剔除数据中包含的随机干扰误差即噪声污染，得到真实值的最优估计[9]。大坝变形监测序列可以看作是一个随机离散系统，随机线性离散系统的卡尔曼滤波方程表达式为：

xk+1=Ak+1 | kxk+wk

(1)

zk+1=Ck+1xk+1+vk+1

(2)

式中：xk为tk时刻状态向量；zk+1为tk+1的观测向量；Ak+1|k为tk时刻至tk+1时刻的状态转移矩阵；Ck+1为tk+1时刻的观测矩阵；wk为系统噪声向量；vk+1为观测噪声向量。

系统噪声向量wk和观测噪声向量vk的统计特性满足以下条件：

(3)

式中：Q(k)为系统噪声向量的方差矩阵；R(k)为观测噪声向量的方差矩阵；δkj为狄克拉函数，当k=j时，δij=1，当k≠j时，δkj=0。

(4)

Pk=[I-KkCk]Pk|k-1

(5)

其中：

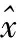
(6)

Pk|k-1=Ak|k-1Pk-1ATk|k-1+Qk-1

(7)

Kk=Pk|k-1CTk[CkPk|k-1Ck+Rk]-1

(8)

式(4)～(8)即为随机线性离散系统卡尔曼滤波的基本方式。

2 ARIMA模型

ARIMA模型又称博克斯-詹金斯模型，是一种时间序列预测方法。近些年，该模型广泛应用于大坝变形预测领域，它不仅可以考虑变形监测数据在时间序列上的依存性，还可以考虑数据受到随机干扰的波动性，从而能够较为准确地进行大坝变形的预测。时间序列基本模型包括自回归模型(AR)、移动平均模型(MA)和自回归滑动平均模型(ARMA)[10]，这3种模型都是针对平稳时间序列而言的，而大坝变形监测数据一般都是非平稳的，包含长期趋势、季节波动、循环波动和不规则变动，故需要对原数据进行有限次差分处理后产生一个平稳的时间序列，再进行建模。ARIMA模型正是基于此思想对非平稳数据进行处理与建模的，ARIMA(p,d,q)中，AR代表自回归模型，MA代表滑动平均模型，I表示差分，p为自回归阶数，d为差分次数，q为滑动平均阶数，其数学表达式为：

Φ(B)▽dxt=Θ(B)εt

(9)

其中：

Φ(B)=1-Φ1B-Φ2B2-…-ΦpBp

(10)

Θ(B)=1-Θ1B-Θ2B2-…-ΘpBp

(11)

▽=1-B

(12)

式中：xt(t=1,2,3,…)为时间序列；εt为均值是0，方差是σε的正态白噪声过程；Φi(i=1,2,…,p)和Θj(j=1,2,…,q)为模型的待估系数；B为后移差分算子。

3 大坝变形预测的Kalman-ARIMA模型

3.1 卡尔曼滤波处理分析

大坝变形监测数据属于随机线性离散系统，本文采用(α-β)卡尔曼滤波模型[11]，即将监测点的变形和变形速度看成状态参数，由于大坝变形量比较小，其加速度也很小，故将变形加速度看成动态噪声向量，则状态方程和观测方程为：

(14)

3.2 时间序列分析与建模

时间序列模型常用的建模方法有Box-Jenkins法、Pandit-Wu S.M法(也称为DDS法)以及长自回归、白噪化法等，针对大坝变形监测数据，可采用Box-Jenkins法建立ARIMA模型[12,13]，其步骤如下：

(1)平稳化。运用差分法或将数据先进行对数变换再进行差分运算，提取大坝变形监测数据序列中的确定性信息，使其自相关函数呈现指数衰减(即拖尾)的特征以达到平稳的目的。

(2)识别并估计模型，包括模型识别、模型定阶及参数估计。模型识别是在一定标准下(如序列是零均值过程)，根据样本自相关函数(ACF)和样本偏自相关函数(PACF)的形式，结合残差方差图、最佳准则函数(AIC准则、SBC准则和BIC准则)等定阶法，确定ARMA模型的p、q值。然后利用矩估计、最小二乘估计或极大似然估计法对所建ARMA模型进行参数估计。

(3)诊断，包括模型的适应性检验和参数的显著性检验。模型的适应性检验的实质为检验被估模型残差的独立性。若残差序列为白噪声序列，说明拟合模型准确刻画了时间序列过程，显著有效；若残差序列不是白噪声序列，说明拟合模型不显著，相关信息有残留，则返回步骤(2)，重新估计p、q值并建模，再进行参数检验。参数的显著性检验，即检验模型中每一个未知参数是否显著为零。当变量的参数不显著时，将该变量从模型中剔除，重新进行(2)。

(4)预测。通过诊断检验的模型即可用于大坝变形预测。

诊断这一步骤极为必要，样本的自相关函数和偏自相关函数只对时间序列ARMA(p，q)过程的识别起指导作用，尤其当p，q都不为0时，识别难度较大，还需借助系统的物理背景和先验知识及实验技巧和经验。

4 工程实例分析

某水电站位于皖南长江支流青弋江上游，是一座综合性中型水利水电枢纽工程。枢纽包括大坝、溢洪道、泄洪中孔、泄水底孔、发电厂房和筏道。大坝是一座同心圆变半径的混凝土重力拱坝，坝顶高程为126.3 m，最大坝高为76.3 m，坝顶弧长419 m，坝顶宽8 m，最大坝底宽53.5 m。经过一次大坝安全监测系统更新改造后，该工程具备了一套以变形观测为主的大坝观测系统。大坝共布置了16个倒垂线测点用来监测坝基和F11、F32大断层及两坝肩岩体的变形。本文选取处于8号坝段的一个测点从2013年1月1日到2013年5月27日的位移观测值进行分析，共计147个位移值。其中将前137个实测值作为已知数据，后10个实测值作为未来实际位移值。首先对已知数据进行卡尔曼滤波处理，再对滤波后的数据建立ARIMA模型，并进行未来10个位移的预测，然后把位移预测结果与单纯用ARIMA模型对原数据进行预测的结果作对比，从而验证本文提出的Kalman-ARIMA模型在大坝变形预测上的合理性和适用性。

利用3.1节所述的针对大坝变形数据的卡尔曼滤波法对已知位移数据进行滤波处理，结果如图1所示，并统计已知位移值与滤波值之间的残差，发现绝大多数残差值在±0.01 mm以内，而且滤波值反应的变化规律与实测位移值基本一致，说明该卡尔曼滤波过程是对原始观测位移数据进行了一个很好的平滑处理，剔除噪声的效果较好[14]。

图1 位移实测值与卡尔曼滤波值对比Fig.1 Comparison of the observed and kalman filter values

根据3.2节所述ARIMA模型的建立方法对位移实测值进行建模，模型参数p,d,q分别为0,1,1。对卡尔曼滤波后的位移数据进行建模，模型参数p,d,q分别为0,1,0。利用ARIMA(0,1,1)模型对实测数据进行预测，利用ARIMA(0,1,0)模型对卡尔曼滤波后数据进行预测，结果见表1和图2。可以看出，对位移实测值进行卡尔曼滤波处理，然后再进行ARIMA模型的建立并预测，可以有效地减小预测值与实际原位移之间的残差绝对值和残差标准差，从而提高大坝位移的预测精度，产生这个效果的主要原因可以分析为：卡尔曼滤波过程可以剔除观测过程中随机干扰噪声对监测数据的影响，使得滤波后的数据更加逼近真实值，对大坝较为真实的位移值进行建模可以较为准确地反应坝体力学机理对位移的影响，从而可以更加精确地进行变形预测。由此说明，Kalman-ARIMA模型应用在大坝变形预测上是合理有效的。

表1 实测数据预测值与卡尔曼滤波后数据预测值对比Tab.1 Comparison of the predictive values between observed and kalman filter data

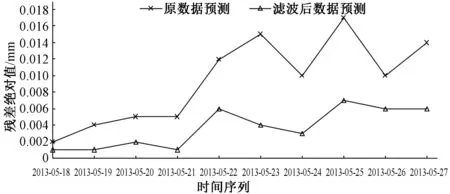
图2 两种方法的残差绝对值对比Fig.2 Comparison of the absolute residuals from the two methods

5 结 语

卡尔曼滤波是一种对动态观测数据进行实时处理的有效办法，可以剔除观测过程中随机干扰噪声对数据精度的影响，从而可以获得更加接近真实值的观测数据。本文提出卡尔曼滤波与ARIMA模型相结合的预测方法，即利用卡尔曼滤波对大坝原始变形数据进行滤波处理，再根据对滤波后的数据进行建模计算并预测。结合具体大坝位移观测数据分析，结果表明，Kalman-ARIMA模型能够有效地剔除大 坝位移数据中的随机干扰噪声，并得到比较精确的预测结果，因此，该模型在大坝变形预测方面具有推广价值。

□

[1] 吴中如．水工建筑物安全监控理论及其应用[M]．南京：河海大学出版社，2003．

[2] 顾冲时，吴中如．大坝与坝基安全监控理论和方法及其应用[M]．南京：河海大学出版社，2006．

[3] 何金平．大坝安全监测理论与应用[M]．北京：中国水利水电出版社，2010．

[4] 沈细中，张文鸽，冯夏庭．大坝变形预测的ANFIS 模型[J]．岩土力学，2006，27(增)：119-122．

[5] 张 豪，许四法．基于经验模态分解和遗传支持向量机的多尺度大坝变形预测[J]．岩石力学与工程学报，2011，30(增2)：3 681-3 688．

[6] 李守巨，刘迎曦，刘玉静．基于进化神经网络混凝土大坝变形预测[J]．岩土力学，2003，24(4)：635-638．

[7] 张志鹏，王伟平，郑海超．卡尔曼滤波及其在时间序列预测中的应用[J]．仪表技术，2010,(7)：37-39．

[8] 颜可珍，张 邹，林 峰．卡尔曼时间序列模型预测路面平整度指数[J]．路基工程，2012,(4)：1-3．

[9] Sinopoli B, Schenato L, Franceschetti M, et al. Kalman filtering with intermittent observations[J]. Automatic Control, IEEE Transactions on, 2004,49(9):1 453-1 464.

[10] 潘迪夫，刘 辉，李燕飞．基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型[J]．电网技术，2008，32(7)： 82-86．

[11] 王 利，李亚红，刘万林．卡尔曼滤波在大坝动态变形监测数据处理中的应用[J]．西安科技大学学报, 2006,26(3)：353-357．

[12] 张树京，齐立心．时间序列分析简明教程[M]．北京：清华大学出版社，2003．

[13] 肖枝洪，郭明月．时间序列分析与SAS应用[M]．武汉：武汉大学出版社，2012．

[14] 王井利，张春哲．自适应卡尔曼滤波在地铁监测中的应用[J]．沈阳建筑大学学报：自然科学版，2014,(2)：263-268．