基于支持向量机的干旱区月潜在蒸散发的模拟

杨会娟，粟晓玲，郭 静(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

0 引 言

潜在蒸散发量是衡量大气蒸散发能力的重要指标，也是估算作物需水量、生产潜力和制定灌溉制度的重要依据。此外，由于其对地表能量平衡和水量平衡的影响，也是建立流域水文模型及水量平衡模型时必须考虑的水文变量[1,2]。对一些气候模式和大气环流模式的研究发现，潜在蒸散发极易受到气候因素变动的影响[3]。目前计算潜在蒸散发应用最多的且较精确的是联合国粮农组织推荐的基于气象数据的Penman-Montieth公式[4](简称PM公式)，但该公式需要湿度、风速、温度、日照时数等多个气象因子，而在一些气象站，风速数据或者缺失或者精度存在问题[5]，一些ET0自动估测系统，难以用低成本测量传感器测量日照时数，限制了其在缺少风速和日照时数两气象因子的站点的应用。

潜在蒸散发是各气象因子的非线性复杂函数[6]，采用人工智能方法模拟非线性关系已得到广泛应用。很多学者应用人工神经网络(ANN)方法模拟潜在蒸散发，如邹磊等[7]在河南省选择了5个典型区域，建立了基于温度及辐射资料的RBF神经网络模拟模型，取得了较高的模拟精度；Kuo等[8]以嘉南灌溉协会实验站的气象观测数据作为输入变量，利用ANN对Penman-Monteith方法和蒸发皿蒸发量的方法研究比较，结果表明，基于Penman-Monteith公式的BP-ANN模型可以精确的预测蒸散发；Jahanbani等[9]根据伊朗北部的拉什特市的1975-1985年的最高和最低的日气温资料，使用基于贝叶斯正则化的FFBP模型预测了该地区当前月份和下一个月的蒸散发，取得了较高的预测精度，发现ANN模型的预测精度优于HGS模型；El-Shafie等[10]提出了预测日蒸散量的集成神经网络模型(ENN)，依据伊朗北部的拉什特市和马来西亚柔佛的新山市的最低和最高的日气温进行模拟预测，结果表明，ENN模型预测日ET0的效果优于经典的MLP-ANN方法。也有一些学者尝试采用支持向量机(SVM)模拟潜在蒸散发[11,12]或实际蒸散发[13]，取得了较好的模拟效果。SVM作为一种简单实用的方法，与ANN相比，SVM能够很好地克服前者训练时间长，训练结果存在随机性和过学习等不足[14]。当观测的气象因子缺乏风速和日照时数时，SVM模拟潜在蒸散发的精度能否满足要求尚未知。兹采用支持向量机回归方法，以我国西北干旱区石羊河流域为例，分别建立输入6个气象因子和4个气象因子的潜在蒸散发模拟模型，并比较模拟精度，评价模型的适用性。

1 研究方法与资料

1.1 Penman-Monteith方程

Penman-Monteith方程考虑了影响ET0的各种气象因素，物理基础可靠，不需要专门的地区率定和风函数等，使用一般气象资料(湿度、风速、温度和日照时数)即可计算潜在蒸散发量。Penman-Monteith公式[15]如下：

(1)

式中：ET0为潜在蒸散发量，mm/d；Rn为输入冠层净辐射量，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；T为空气平均温度，℃；u2为2 m高处风速，m/s；es为饱和水汽压，kPa；e0为实际水汽压，kPa；Δ为饱和水汽压与温度关系曲线在某处的斜率，kPa/℃；γ为干湿温度计常数，kPa/℃。

1.2 支持向量机回归(SVR)

SVR最初主要用于解决模式分类识别问题[16,17]。 但分类问题和回归问题在原理上是一样的，对于一个输入都有相应的输出，也相当于一个函数映射关系，其基本原理为：

假定样本的训练集为{(x1,y1),(x2,y2),…,(xn,yn)}，其中i=1,2,…,n，xi∈Rd是n个d维向量，yi∈R。xi为样本的输入值，yi为输出值。通过训练学习找到一个非线性回归函数f，使得对于训练样本集和预测数据集均满足yi=f(xi)。利用非线性映射ψ将输入的训练数据映射到高维特征空间，然后在该空间进行线性回归。设需要求解的SVR函数为：

f(x)=ω·ψ(x)+b

(2)

式中：ψ(x)为映射函数；ω为权值向量，其维数为高维空间的维数；b∈R，为偏置。

可通过最小化下面的风险函数来求函数估计问题：

(3)

式中：‖w‖2为描述函数；c为惩罚系数，为对超出误差ε的样本的惩罚度，c越大表示对训练误差超出ε的样本的惩罚越大，用于逼近误差的折中和控制模型复杂度；ξ,ξ*为考虑允许拟合误差而引入的松弛变量；ε为回归函数的输出误差要求，ε越小，回归函数的输出误差越小，拟合精度越高。

这是一个凸二次规划优化问题，采用Lagrange乘子法和核函数技术，引入α和α*，将上述问题转换为其对偶形式进行求解：

(4)

再利用KKT条件求得偏置b为 ：

(5)

最后代入原方程得支持向量机回归方程为：

(6)

若αi-α*i不为零，则该值所对应的样本即为支持向量。这里K(xi,x)为核函数，在最优分类面中采用适当的内积函数K(xi,x)就可以实现某一非线性变换后的线性回归，但核函数一定要满足Mercer条件，其值等于向量Xi在特征空间ψ(xi)和ψ(x)的内积。核函数的引入，使得函数求解绕过特征空间，直接在输入空间上求和。本文选用的核函数为RBF核函数，其形式为：

K(x,xi)=e(-g‖x-xi‖2)g>0

(7)

1.3 资料来源

研究所用到的气象资料有河西走廊东段石羊河流域乌鞘岭、民勤、永昌、武威、古浪共5个气象站的1959―2009年的长系列逐日的平均气温、最低气温、最高气温、平均风速、日照时数、相对湿度。其中古浪站的资料来源于甘肃省气象局，其余气象站资料来自于中国气象科学数据共享服务网。各气象站的地理位置见表1。

表1 石羊河流域各气象站地理位置Tab.1 Location of all meteorological stations in Shiyang River Basin

1.4 模型评价

选择平均绝对误差MAE(mm)、均方根误差RMSE(mm)、相关系数R以及确定性系数DC作为模型模拟精度的评价标准。

(8)

(9)

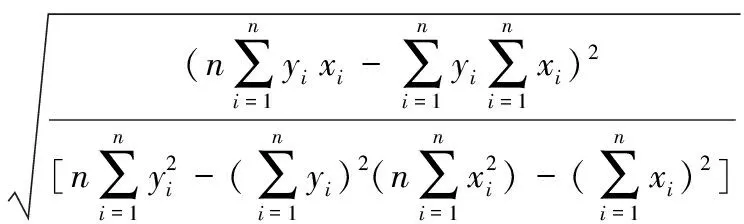
(10)

(11)

2 模型应用

2.1 六因子输入的月潜在蒸散发量的模拟精度评价

以平均气温、最低气温、最高气温、平均风速、日照时数、相对湿度6个气象因子作为SVR模型和ANN模型的输入，模拟石羊河流域5个气象站月潜在蒸散发量，以1999―2008年共10年(120个月)的序列为训练期，2009年(12个月)为验证期。

图1为SVR模型模拟的月潜在蒸散发量与Penman-Monteith方程计算值的对比，可以看出，各站SVR模型模拟值与PM公式计算值拟合较好，除乌鞘岭站外，其余4站在高值(>120 mm/月)区模型模拟值较计算值偏低，月潜在蒸散发高值主要分布在夏季5―8月。表2和表3分别为SVR模型和ANN模型模拟月潜在蒸散发量时训练期和验证期的性能指标值，可以看出，SVR模型和ANN模拟精度都较高，在训练期和验证期有较小的RMSE、MAE和较高的R和DC值，各站的相关系数R和确定性系数DC均在0.9以上。故在模拟该流域的月潜在蒸散发量时两个模型都可以应用。

图1 训练期六因子输入SVR模型月潜在蒸散发量模拟值与PM公式计算值的对比Fig.1 The comparison of monthly potential evapotranspiration between SVR model and calculation value

表2 六因子输入SVR模型的RMSE、MAE、DC以及R值Tab.2 The RMSE、MAE、DC and R values of SVR model

2.2 四因子输入的月潜在蒸散发量的模拟精度评价

为了探索资料较少地区潜在蒸散发量计算的新方法，进行了基于平均温度、平均最高气温、平均最低气温、平均相对湿度4个因子的月潜在蒸散发量的模拟。

表3 六因子输入ANN模型的RMSE、MAE、DC以及R值Tab.3 The RMSE、MAE、DC and R values of ANN model

图2为四因子SVR模型模拟的月潜在蒸散发量与Penman-Monteith方程计算值的对比，可以看出，各站SVR模型模拟值与PM公式计算值拟合较好，除乌鞘岭站外，其余4站在高值点(>140 mm/月)模型模拟值较计算值偏低。表4为四因子SVR模型模拟月潜在蒸散发量时训练阶段和验证阶段的性能指标值，可以发现，以四因子为输入模拟月潜在蒸散发量时，不论在训练期还是验证期，各站的模拟性能指标尽管略低于六因子输入条件下的性能指标，但相关系数R和确定性系数DC依然在0.9以上，模拟精度较高。故在缺少风速和日照资料的情况下，可用支持向量机回归模型进行月潜在蒸散发量的模拟。

图2 训练期四因子输入SVR模型月潜在蒸散发量模拟值与PM公式计算值的对比Fig.2 The comparison of monthly potential evapotranspiration between SVR model and calculation value

表4 四因子输入SVR模型的RMSE、MAE、DC以及R值Tab.4 The RMSE、MAE、DC and R values of SVR model

3 结 论

采用Penman-Monteith方程计算了石羊河流域5个气象站的潜在蒸散发，建立了六因子和四因子输入的支持向量机回归模拟模型。通过比较发现，四因子输入的SVM模型模拟月潜在蒸散发的精度尽管略低于六因子输入的模型精度，但相关系数和确定性系数依然高于0.9，说明SVM模型可以应用于干旱区缺乏风速和日照时数的观测站的潜在蒸散发的模拟。这与侯志强、郭淑海[11,13]等人的研究成果相一致，即随着输入气象因子的减少，模型的模拟精度会降低，但仍具有一定的适用性。此外，本研究还建立了六因子和四因子输入的年支持向量机回归模拟模型，由于篇幅所限，在此未能一一列举。这两个模拟模型的精度也较高，但同上述研究结果一样，六输入因子模型的模拟精度要高于四输入因子模型。

研究也发现SVM模拟月潜在蒸散发时，在5-7月份潜在蒸散发较高时，模拟值相比PM公式计算值偏低，这与模型的参数选择有关，并不影响模型的使用。用支持向量机做回归模拟时，惩罚参数c和核函数g的选择十分重要，可进一步研究基于粒子群、遗传算法、蚁群算法等智能方法实现SVM参数优化，提高SVM的模拟效果。另外本文仅探索了月潜在蒸散发量的模拟效果，在以后的研究中，可进一步探讨支持向量机回归模型模拟日潜在蒸散发量的有效性。

□

[1] 张 东，张万昌，徐全芝．汉江上游流域蒸散量计算方法的比较及改进[J]．资源科学，2005，27(1)：97-103．

[2] 侯兰功，肖洪浪，邹松兵，等．额济纳绿洲生长季参考作物蒸散发敏感性分析[J]．中国沙漠，2011，31(5)：1 255-1 259．

[3] 张 勃，张调风．1961-2010年黄土高原地区参考作物蒸散量对气候变化的响应及未来趋势预估[J]．生态学杂志，2013，32(3)：733-740．

[4] 李 禄，迟道才，张政利，等．太子河流域参考作物腾发量演变特征及气候影响因素分析[J]．农业工程学报，2007，23(9)：34-38．

[5] Laaboudi A & Mouhouche B & Draoui B．Neural network approach to reference evapotranspiration modeling from limited climatic data in arid regions[J]．International Journal of Biometeorology．2012，56：831-841．

[6] 粟晓玲，宋 悦，牛纪萍，等．泾惠渠灌区潜在蒸散发量的敏感性及变化成因[J]．自然资源学报，2015，30(1)：115-123．

[7] 邹 磊，夏 军，马细霞，等．潜在蒸散发量估算方法在河南省的适用性分析[J]．水文，2014，34(3)：17-23．

[8] Kuo SF，Chen FW，Liao PY，Liu CW．A comparative study on the estimation of evapotranspiration using backpropagation neural network：Penman-Monteith method versus pan evaporation method[J]．Paddy and Water Environment，2011，9(4)：413-424．

[9] Jahanbani H，El-Shafie A．Application of artificial neural network in estimating monthly time series reference evapotranspiration with minimum and maximum temperatures[J]．Paddy and Water Environment，2011，9(2)：207-220．

[10] El-Shafie A，Najah A，Alsulami HM，et al．Optimized Neural Network Prediction Model for Potential Evapotranspiration Utilizing Ensemble Procedure[J]．Water Resources Management，2014，28：947-967．

[11] 侯志强，杨培岭，苏艳平，等．基于最小二乘支持向量机的ET0模拟计算[J]．水利学报，2011，42(6)：743-749．

[12] 陈大春，曹 伟，雷晓云．基于最小二乘支持向量机的参考作物潜在蒸散量估计[J]．新疆农业大学学报，2012，34(5) ：431-436．

[13] 郭淑海，杨国靖，李清峰，等．新疆阿克苏河上游高寒草甸蒸散发观测与估算[J]．冰川冻土，2015，37(1)：241-248．

[14] 顾燕萍，赵文杰，吴占松．最小二乘支持向量机的算法研究[J]．清华大学学报(自然科学版)，2010，50(7)：1063-1066．

[15] Allen，RG，Pereira，LS，Raes D, et al．Crop evapotranspiration guidelines for computing crop water requirements[R]．FAO Irrigation and Drainage Paper 56，Rome，1998．

[16] 王小川，史 峰，郁 磊，等．MATLAB神经网络43个案例分析[M]．北京：北京航空航天大学出版社，2013．

[17] 黄巧玲，粟晓玲．基于小波支持向量机耦合的月径流预测方法[J]．水力发电学报，2015，34(3)：1-8．