基于AHP和改进熵权法的城市节水状况综合评价研究

周振民，李延峰，范 秀，管 财，宋相松

(1.华北水利水电大学，郑州 450011；2.新乡市大功引黄工程管理处，河南 新乡 453300)

0 引 言

我国水资源短缺，时空分布不均，水资源浪费及水资源污染现象严重，水资源管理粗放，这一系列问题加剧了我国水资源的紧缺，缺水已成为制约经济发展和社会进步的重要因素。在这种情形下，采取合理有效的评价方法对城市节水状况进行综合评价，对制定出切实可行的节水目标、措施、决策等以改善城市节水状况、提高城市节水效率、建设节水型城市具有重要的现实意义。城市节水常用的评价方法有AHP、AHM、云模型、改进熵权法、集对分析法等，每种评价方法各有利弊。本文根据城市节水评价指标体系的特点，为提高其综合评价的有效性及可信度，首先建立了AHP和改进熵权法，构建了模糊评价模型。随后应用构建模型，对郑州市城市节水状况进行了综合评价。研究结果对于指导城市节水、建立节水型社会，落实最严格水资源管理三条红线具有十分重要的参考价值。

1 理论基础研究

1.1 层次分析法

层次分析法[1-3](Analytic Hierarchy Process，简称AHP)是20世纪70年代由美国匹兹堡大学著名运筹学家撒汀(T. L. Saaty)等人提出的一种对复杂问题进行定性定量相结合的简明有效的多准则决策方法。

层次分析法确定权重[4]的步骤如下：

(1)明确所分析的问题，建立递阶层次结构。理清问题的范围、所包含的因素及其相互之间的联系，确定所解决问题的目的，从而建立从高到低的层次结构：目标层、准则层、方案层。需要时，可以进一步建立子准则层。

(2)构造判断矩阵。构造一个合理有效的判断矩阵，对正确运用层次分析法起着举足轻重的作用。按照心理学的研究引入9分位标度法。9分位各标度含义如表1所示。

表1 9分位标度Tab.1 9 Point scale

从相同到极强每相邻两个等级之间可依次用2，4，6，8将其量化，即bij可取1～9或它们的倒数。因此，判断矩阵又称正互反矩阵，并且满足下列条件bij>0，bii=1，bij=1/bji，i,j=1,2，…，n。

(3)计算判断矩阵的最大特征值及其特征向量。在权重的计算过程中允许有一定范围的误差存在，在计算判断矩阵的最大特征值及其特征向量时，常采用方根法及和积法。

本文运用方根法确定权重，其步骤如下：

①把判断矩阵每一行的元素求积，然后开n次方，即：

(1)

式中：n为矩阵阶数。

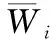
(2)

式中：Wi为所求的各评价指标的权重。

③计算判断矩阵的最大特征值λmax。

(3)

式中：(BW)i表示BW的第i个分量。

④一致性检验。首先，计算一致性指标CI：

(4)

然后从表2查得同阶矩阵平均随机一致性指标RI的值，进行一致性比例CR(其CR=CI/RI)的计算与判断。随机一致性指标RI的值，撒汀用了大小500个子样，对不同的n得到如表2所示的结果。

当CR=0时，可认为判断矩阵的层次排序具有绝对的一致性；当CR<0.1时，可认为判断矩阵的层次排序具有满意的一致性；当CR≥0.1时，可认为判断矩阵的层次排序不具有满意的一致性，应予以修正。

表2 平均随机一致性指标Tab.2 Mean random consistency index

1.2 改进熵权法

熵的定义来自于热力学，后来被引入到信息论中，广泛应用于方案优选、多目标决策及各种评价，信息熵被看作是确定权重的一种极为可靠有效的方法。熵权法[5,6]是一种客观的赋权方法，在进行熵权法赋权时需对数据进行标准化处理。

改进熵权法确定权重的步骤如下：

(1)构造归一化的判断矩阵。设m个评价对象，n个评价指标，构建原始判断矩阵：

A=(aij)m×n

(5)

式中：aij表示第i个评价对象在第j个评价指标上的对应数值。

按不同评价要求将评价指标分为正向指标和负向指标，并对指标数据进行标准化处理，得到判断矩阵：

R=(rij)m×n

(6)

式中：rij为aij归一化后的数据，rij∈[0,1]。

对于正向指标(即越大越优型)，按下式进行归一化处理：

(7)

对于负向指标(即越小越优型)，按下式进行归一化处理：

(8)

(2)确定评价指标的熵值及熵权：

(9)

其中：

由上式确定了第j个评价指标的熵值之后，可由下式算得该指标的熵权：

(10)

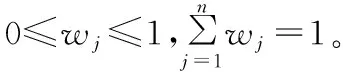
(3)权重的确定及其一致性检验。评价指标权重的确定直接关系到评价结果的准确度。由式(2)算得的熵权彼此独立，但未体现出由信息熵所确定的各评价指标初始权重是否具有良好的一致性，对此需要构造模糊互补判断矩阵对其进行改进，即：

M=(mij)n×n

(11)

式中：mij为评价指标i对j的优先关系系数，0≤mij≤1，mij+mji=1，mij>0.5、mij=0.5、mij<0.5分别表示i优于j、i等于j、i劣于j。

对于上式必须进行一致性检验，一致性指标的计算公式如下：

(12)

给定一个阈值δ，当μ<δ时，即可认为M具有满意的一致性；当μ=0时，即可认为M具有完全的一致性；当μ≥δ时，即可认为M不具有满意的一致性，需要予以修正。

1.3 综合权重的确定

在权重计算上，本文将AHP和改进熵权法相结合，即实现主观和客观的融合，从而使评价指标权重的计算结果更具有科学性、有效性及导向性。将其两者的权重相乘，并进行标准化处理，即可得到各评价指标对目标层的综合权重[7]：

W=(wi)1×n

(13)

式中：n为评价指标的个数。

2 模型构建

2.1 构建隶属函数

由于主观指标缺乏一定的客观性、难以量化等缺点，因而本文中评价指标体系选用的均为定量指标。隶属函数是对模糊概念的一个定量描述，正确构建隶属函数是运用模糊集合理论解决问题的根基。采用模糊隶属函数法，对其正指标和逆指标分别采用戒上行和戒下行的隶属函数。对于隶属函数中的参数，分别用a、b表示函数的上下限(分别为各评价指标集合的最大及最小值)。

建立评价指标所适用的隶属函数，如公式(14)、(15)所示。

正指标采用公式：

(14)

逆指标采用公式：

(15)

根据相应的指标隶属度分级评价标准表，把实际指标值代入对应的隶属函数中，即可得出相应的隶属度值。

2.2 建立模糊评价矩阵

运用隶属函数对各评价指标进行隶属度的计算，使其各评价指标均被统一到无量纲的0～1之间，便于用统一的方法进行综合评价。经处理化的数据，k个评价对象对应于n个评价指标的隶属度构成模糊评价矩阵：

L=(lij)Tk×n

(i=1,2,…,k;j=1,2,…,n)lij∈(0,1)

(16)

2.3 层次模糊综合评价模型

在确定了各评价指标的最终权重及隶属度后，即可进行城市节水状况的综合评价，其计算公式为：

S=WL=(wi)1×n(lij)Tk×n

(17)

式中：S为城市节水状况综合评价结果，其值越大表明城市的节水状况越好；W为评价指标的综合权重所构成的矩阵；L为评价指标隶属度所构成的矩阵。

根据所制定的评语集范围，可查得综合指标值所在区域，即评价对象所处的等级。依据节水型城市发生、发展的过程等特点，可将城市的节水状况分为五级，如表3所示。

表3 城市节水状况评价标准Tab.3 Evaluation criteria of urban water saving state

3 城市节水状况综合评价-以郑州市为例

3.1 研究区域概况

郑州市是河南省会，是资源型缺水城市，位于东经112°42′～114°13′，北纬34°16′～34°58′，东西宽166 km，南北长75 km，地处华北平原南部，河南省中部偏北，北临黄河，西依嵩山，东南为广阔的黄淮平原。郑州市横跨中国二、三级地貌台阶，西南部嵩山属第二级地貌台阶前缘，东部平原为第三级地貌台阶的组成部分，山地与平原之间是低山丘陵地带[8]。郑州气候属北温带大陆性季风气候，境内有大小河流124条，流域面积较大的河流有29条，分属于黄河和淮河两大水系。

截至2013年9月底，郑州市辖6个市辖区、5个县级市、1个县。郑州市2013年末总人口919.1万人，郑州市地区生产总值完成6 201.90亿元，年均增长12.1%，总量居河南省第一位、中西部第三位。2013年全市水资源总量6.973 7亿m3，郑州市各种供水工程供水总量15.990 8亿m3，水资源缺水率达到了56.39%。郑州市城镇污水排放总量为6.534 5亿m3，污水处理率不高，仅为56.03%；污水处理回用率更低，仅为15.37%。2013年末，郑州市中型水库蓄水总量5 490万m3，比年初的蓄水总量减少2 068万m3。郑州市区的浅层和中深层地下水降落漏斗均呈扩大趋势。从总体上看，郑州市的水资源呈紧缺态势。

3.2 构建评价指标体系

遵循着科学性、系统性、可操作性、代表性及不重复且易量化等指标选择原则，对城市节水指标进行有效的筛选。为对城市节水状况有一个客观合理的评价，经过相关资料的查阅及进一步的研究，考虑了6项节水因素，建立了如表4所示的城市节水状况评价指标体系[9-11]。

3.3 指标权重的确定及分析

3.3.1层析分析法确定权重

(1)构造判断矩阵。在有关专家、学者等评分的基础上，再依据1～9标度法，将整个系统中各递阶层次中的因素进行两两比较分析。

准则层对目标层的判断矩阵，各指标层H1～H5、P1～P4、R1～R4、K1～K3、N1～N3、S1～S3对准则层H、P、R、K、N、S的判断矩阵分别为：

表4 城市节水状况评价指标体系Tab.4 Evaluation index system of urban water saving state

(2)层次单排序、总排序及其一致性检验。经过计算得准则层对目标层，各指标层H1～H5、P1～P4、R1～R4、K1～K3、N1～N3、S1～S3对准则层H、P、R、K、N、S的权重分别为：

判断矩阵的数值是由待评价区历年文献资料所得，加之评判专家和学者的意见和认识，综合权衡之后得出的。由于人们认识的多样性，客观世界的复杂性以及在对因素进行比较时没有固定的参照标准，难免会做出与实际情况不符的判断。因此，很有必要对所构造的判断矩阵进行一致性检验。经计算得各判断矩阵的随机一致性比率CR分别为0.060 5、0.016 0、0.089 3、0.007 8、0.055 9、0.015 8、0.015 8，其值均小于0.1，由此可见各判断矩阵均具有满意的一致性。

根据准则层权重及指标层中各因素的权重计算结果，进一步得到指标层各因素对目标层的层次总排序经归一化后的综合权重为WA=(0.039 6, 0.109 6, 0.024 1, 0.070 6, 0.039 6, 0.034 6, 0.009 0, 0.052 6, 0.019 4, 0.084 2, 0.139 3, 0.023 7, 0.045 2, 0.094 7, 0.040 7, 0.010 5, 0.072 6, 0.041 5, 0.015 8, 0.014 4, 0.005 5, 0.012 6)。

对该层次总排序进行一致性检验，计算得CI=0.027 4,RI=0.852 7,CR=0.032 1﹤0.1，故层次总排序也具有满意的一致性，因而可以确认所计算的权重值是可以接受的。

3.3.2改进熵权法确定权重

选取郑州市为评价对象，根据式(9)、(10)计算得各评价指标的客观权重为WB=(0.040 4, 0.090 5, 0.034 2, 0.062 1, 0.049 5, 0.049 7, 0.020 8, 0.068 9, 0.008 3, 0.060 6, 0.108 6, 0.041 5, 0.061 6, 0.060 6, 0.030 6, 0.022 7, 0.054 8, 0.034 9, 0.028 4, 0.034 2, 0.012 0, 0.024 9)。

根据公式(11)、(12)进一步计算得一致性指标μ=0.014<0.1，故所构造的判断矩阵具有满意的一致性。

3.3.3综合权重的确定

在权重计算上，依据式(13)得到各评价指标对目标层的综合权重为W=(0.025 7, 0.159 0, 0.013 2, 0.070 3, 0.031 4, 0.027 6, 0.003 0, 0.058 2, 0.002 6, 0.081 9, 0.242 6, 0.015 7, 0.044 7, 0.092 0, 0.019 9, 0.003 8, 0.063 8, 0.023 2, 0.007 2, 0.007 9, 0.001 1, 0.005 0)其各指标综合权重之间的比较如图1所示。

图1 各评价指标对目标层的综合权重比较Fig.1 Comprehensive weight value comparison of evaluation index to target layer

3.4 评价指标隶属度

评价指标隶属度是表明评价指标隶属于城市节水状况的程度，对于城市节水指标体系中的定量指标，采用模糊隶属函数法确定其隶属度。经过隶属函数处理后，转化为无量纲的0～1之间的数值。在参考文献的基础上经过专家和学者评议，建立各评价指标的隶属度分级评价标准(即适用于隶属度计算的评价标准表)，详见表5。

表5 城市节水评价指标的隶属度分级评价标准Tab.5 Evaluation criteria of membership grade ofurban water saving evaluation index

采用式(14)、(15)，对应表5的评价标准，依照2013年《郑州市水资源公报》和《郑州市统计年鉴》等相关的统计数据，计算得出各项评价指标2013年对应的数值，其隶属度所构成的矩阵为L=(0, 1.000 0, 0.922 2, 1.000 0, 0, 1.000 0, 0.955 0, 1.000 0, 1.000 0, 0.514 7, 0, 0.038 6, 1.000 0, 0.756 4, 0.814 0, 0.322 4, 1.000 0, 0.435 0, 1.000 0, 0.323 4, 1.000 0, 0.315 6)T。

3.5 城市节水状况综合评价

根据层次模糊综合评价模型，可得郑州市节水状况的综合评价结果为S=W·L=0.5936，再依据表3中所划分的城市节水状况评价标准，其评价结果表明郑州市2013年城市综合节水状况处于中等水平，虽然在节水方面取得了一定的成效，但距理想状况仍存较大的差距。从评价结果及图1中各评价指标的权重值比对可以看出，郑州市需从以下方面进一步推进节水型城市建设：①在生态上，加大城市污水处理设施的资金投入与建设，提高城市污水处理回用率；②在工业上，改善工业生产工艺，提高用水效率，降低万元GDP及万元工业增加值用水量；③在生活上，加强节水宣传教育，提高人们的节水意识，降低人们日常生活中的用水量；④在农业上，推广运用喷灌、滴灌、渗灌、微喷等高效节水技术，提高水资源的利用效率，降低亩均灌溉用水量；⑤在经济上，加快城市的经济建设，夯实城市的经济基础，实现节约与发展的良性循环。

4 结 语

(1)采用AHP和改进熵权法组合赋权，使主观与客观相融合，确定评价指标权重更具科学性。

(2)运用该模糊评价模型对郑州市的城市节水状况进行评价，得出郑州市的城市节水状况处于中等水平。从评价结果等方面来看，郑州市仍需进一步加强节水型社会建设，同时也从侧面反映出节水技术是应对水资源危机的根本之策。因而要研发节水新技术，推广运用节水新工艺，建立更加合理的水价体系等，从而促进城市经济健康快速的发展。而坚实的经济实力会为节水型城市建设的良性发展起到积极的保障作用。

(3)该模糊评价模型应用于郑州市进行节水评价，较为合理有效，并对其他城市的节水评价同样具有适用性，对城市节水政策的制定、规划及其措施体系的实施起到一个良好的导向和推动作用。

(4)随着社会经济的发展和人民生活水平的提高，在实际的生产、生活中，其城市节水评价指标体系、评价指标分级标准值等的制定需要做进一步的改进和完善，以更好的适应其发展。

□

[1] 朴春花. 层次分析的研究与应用[D].北京：华北电力大学(北京),2008.

[2] 郭金玉,张忠彬,孙庆云. 层次分析法的研究与应用[J]. 中国安全科学学报,2008,(5):148-153.

[3] 荆全忠,姜秀慧,杨鉴淞,等. 基于层次分析法(AHP)的煤矿安全生产能力指标体系研究[J]. 中国安全科学学报,2006,(9):74-79,145.

[4] 邓 雪,李家铭,曾浩健,等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识,2012,(7):93-100.

[5] 章 穗,张 梅,迟国泰. 基于熵权法的科学技术评价模型及其实证研究[J]. 管理学报,2010,(1):34-42.

[6] 贾艳红,赵 军,南忠仁,等. 基于熵权法的草原生态安全评价——以甘肃牧区为例[J]. 生态学杂志,2006,(8):1 003-1 008.

[7] 陆建红,丁立杰,徐建新. 模糊综合评价模型在农村饮水安全评价中的应用[J]. 水电能源科,2011,(2):99-102,111.

[8] 王慧猛. 郑州市区绿色开放空间分析与优化[D].郑州：河南大学,2013.

[9] 高 鹏. 节约型社会城市节水指标体系及评价方法研究[D].河北保定：华北电力大学(河北),2007.

[10] 肖伟华,许新发,梅亚东. 城市节水指标体系及其评价研究[J]. 江西水利科技,2005,(3):143-148.

[11] 张晓洁. 城市节约用水评价及管理研究[D].合肥：合肥工业大学,2001.