无线网络功率最小化的分布式中继选择方法*
武 航,钱丽萍*,陈庆章,卢为党(.浙江工业大学计算机科学与技术学院,杭州3003;.浙江工业大学信息工程学院,杭州3003)
无线网络功率最小化的分布式中继选择方法*
武航1,钱丽萍1*,陈庆章1,卢为党2
(1.浙江工业大学计算机科学与技术学院,杭州310023;2.浙江工业大学信息工程学院,杭州310023)
摘要:中继协作已视作提高边沿用户能量有效性和服务质量的新型技术。因此,针对存在瑞利衰落的解码转发中继网络如何选择中继节点以最小化系统总功率的问题,提出了使用分布式拍卖算法选择合适的中继节点以最小化系统总传输功率。该算法首先通过信道传输功率的闭合表达式得到用户节点和中继节点的最小传输功率,然后根据分布式拍卖算法为用户节点分配合适的中继节点。仿真结果显示用户节点仅需要通过和中继节点交换少量信息就可以选择合适的中继节点。
关键词:无线网络;中继选择;拍卖算法;多用户多中继
协作无线网络通过使用中继节点改善链路的吞吐量,扩大覆盖范围和降低传输功率[1-2]。这些中继节点可以使用放大转发AF(Amplify-and-For⁃ward)协议和解码转发DF(Decode-and-Forward)协议处理收到的信息[3-4]。如果使用DF,中继节点将会首先解码收到的信息,然后再重新编码后转发出去。如果使用AF,则中继节点仅放大收到的信号后直接转发出去。
目前,中继选择相关研究备受无线通信领域学者的关注[5-17]。这些研究主要是通过选择合适的中继节点以实现不同的网络服务质量要求,如最大化信道容量[5],最小化中断概率[6],最小化传输功率[7]等。Erwu Liu[8]等人结合比例公平调度算法和协作分集提出了比例公平协作算法,通过该算法可以选择使系统吞吐量最大化的中继节点。Amarasuriya[9]等人提出输出阈值多中继选择(OT-MRS)机制,该机制可以选出一个满足信噪比(SNR)要求的中继节点集合。Atapattu[10]研究了在双向转发放大协作网络基础上,通过选择合适中继以最大化链路的最差信噪比。在文献[11]中,作者根据信道协作时中断概率的阈值推导出最优功率分配的闭合表达式。根据该表达式可以迅速选择使传输功率最小的中继节点。孙立旭[12]等人采用拉格朗日乘子法和最陡下降法,提出了在AF模式下基于信道统计特性的中继选择方法,该方法可以使系统的中断概率最小。叶帆[13]等人提出在延时信道中利用过时的瞬时信道状态信息辅助进行中继选择的新方案。张娜[14]等人提出一种根据即时信道信息选择最优中继的策略,通过引入固定退避时隙和改进的随机退避时隙解决中继选择冲突问题。刘顺兰[15]等人提出一种双向中继选择策略,该策略同时考虑中继节点处的接收信噪比和中继节点到目的节点的信道增益两个因素来选择最优中继。虽然文献[8-15]针对无线网络中的不同优化目标提出了多种优化算法,但是这些算法主要针对单源多中继网络系统,而在实际应用中,多源多中继网络的中继选择更为普遍[16-18]。Upadhyay[16]等人使用功率最小化算法选择合适的中继节点。使用该算法选择的中继节点可以使全局传输功率最小。文献[17]提出一种启发式算法最小化中继的功率消耗,实现绿色协作通信。曹傧[18]等人综合考虑系统容量和系统总功率两个方面,提出了一种基于能效(容量/发送功率)最大化的中继分配算法,该算法首先优化各协作链路效能,然后以能效为权值,使用匈牙利算法为各个源节点分配中继以最大化系统能效。虽然文献[16-18]中的算法可以应用于多用户多中继网络系统,但是由于这些算法是通过集中式实现,因此其对单个节点的计算能力要求较高。另外,负责集中式计算的节点由于功耗较大导致其生命周期较短,从而会使整个网络系统过早死亡。
与现有工作不同,本文将研究在瑞利衰落信道下,两跳DF中继网络如何选择中继节点以实现网络总传输功率最小化。具体而言,本文首先根据各个信道的中断概率阈值得出在满足中断概率要求的情况下,用户节点和中继节点的最小发送功率;然后使用分布式拍卖算法(DAA)为每个用户节点选择合适的中继节点;最终得到的分配方案可以使系统的总传输功率最小。本文提出的算法一方面使用了满足信道中断概率时节点的最小发送功率,这对于优化系统总传输功率十分有益;另一方面通过分布式的方案实现算法,这就降低了对单个节点的硬件要求,使得算法更易实现。
1 系统模型
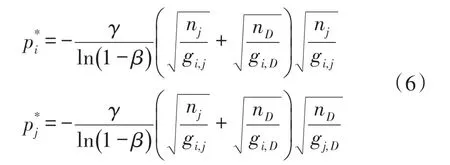
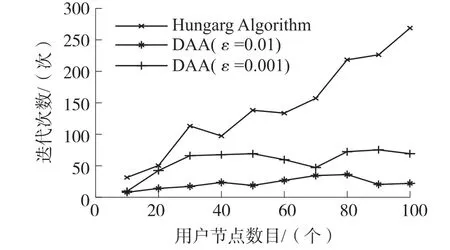
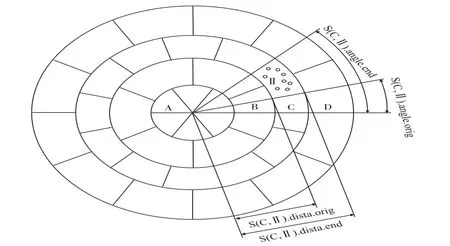
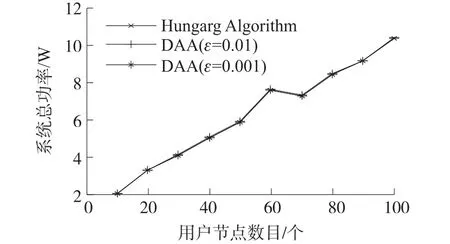
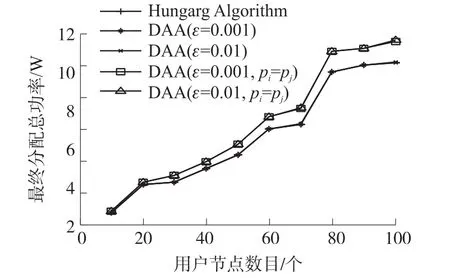
本文考虑一个具有瑞利衰落信道的多用户多中继网络模型,如图1所示。该模型包括N个用户节点,M个中继节点和一个共同的目的节点D,其中用户节点个数N小于中继节点个数M(即N 假设每个中继节点有一个全向天线,能够同时发送和接收数据。hi,j和hj,D分别表示从用户节点i到中继节点j和从中继节点j到目的节点D的信道增益。对于瑞利衰落信道,hi,j和hj,D可以分别用gi,jfi,j和gj,Dfj,D代替。其中,gi,j和gj,D表示路径增益,本文假设gi,j和gj,D是仅和距离相关的常数;fi,j和fj,D用来模拟瑞利衰落信道,本文假设fi,j和fj,D满足均值为1的独立指数分布。 图1 系统模型 当用户i向目的节点发送信息时,将会分两步执行DF协议。首先,用户i以功率pi发送信息xi,用户i的最大发送功率设为SPi,max。然后,如果第j个中继节点负责协作用户i,则该中继将会解码收到的信息,在重新加密之后,以功率pj发送给目的节点D,中继j的最大发送功率设为RPj,max。中继j和目的节点D处的SNR分别为 式中:nj和nD分别表示中继j和目的节点D处的噪声功率。只有当中继j和目的节点D处的SNR均满足要求时,目的节点才能正确的解码收到的信息。假设SNR的阈值为γ,那么用户节点i选择中继j转发信息时,整个链路的中断概率为 因为本文已假设fi,j和fj,D满足均值为1的独立指数分布,所以该中断概率可以进一步表示为 对于一个具有N个用户节点和M个中继节点的无线中继网络,当用户节点i选择中继节点j转发信息时,整个链路的传输功率为pi+pj。因此,用户节点选择不同的中继节点,对应的链路功率也不同。本文将研究如何为用户节点分配中继以使系统的总传输功率最小。假设链路的中断概率阈值为β,则该问题可以描述为 约束条件: 式中:cij=1表示用户i选择中继节点j,cij=0表示用户i不选择中继节点j。保证每一个用户可以选择一个中继节点进行协作传输,表示一个中继节点最多被一个用户选择。 定义一个映射α表示从集合S={1,…,N}到集合R={1,…,M}的映射关系,当且仅当用户i选择中继节点j时,α(i)=j。另外,将中断概率Oij的表达式代入问题(4),同时使用Qij表示,其中和p*j分别表示用户节点i和中继节点j在满足中断概率情况下的最小传输功率,p*i和p*j的具体值将在下文给出。这样就可以将该最小化问题转换为一个最大化问题: 约束条件: 对于问题(5),当找到一个分配使每个用户节点都有一个中继节点且所有用户所选的中继节点都不相同时,如果该分配能够使整个网络系统的Qij之和最大,那么该分配就是使系统总传输功率最小的分配。 3.1计算信道最小传输功率 在问题(5)中,用户节点和中继节点的发送功率是不确定的,因此Qij是未知的。当用户节点i选择中继节点j时,在的条件下,两者在满足中断概率要求时的最小传输功率之和p*i+p*j可以根据定理1求出;在的条件下,信道不能满足最小中断概率的要求,用户节点i也就不可能通过中继节点j和目的节点D通信,所以在这种情况下认为链路ij对应的权重Qij为无穷小。为了便于用户节点选择中继,可以假设该链路对应的权重为根据该假设,若用户节点i不能通过中继j和目的节点D通信,则链路ij对应的权重要远远小于其他链路对应的权重,因此在最大化权重的前提下,用户节点i就不会选择中继j进行协作传输。 反之,用户节点i与中继节点j的最小发送功率之和为,其中: 由于篇幅限制,本文不再对定理1进行证明,详细的证明过程可以参考文献[11]。根据定理1,每个用户节点都可以知道从自身通过每个中继节点到达目的节点所消耗的最小传输功率。因此,我们接下来将利用分布式拍卖原理设计中继选择算法。假设该网络系统中的用户节点和中继节点可以互相收到对方的广播,则用户节点可以和中继节点交换少量的信息。 3.2算法描述 本文所提出的中继选择算法主要是基于分布式拍卖理论。简单而言,中继节点首先计算每条链路在满足中断概率要求时的最小传输功率。然后定义表示中继j的价格,定义表示用户节点i选择中继j时的效益,根据中继的价格,每个用户节点选择一个使其效益最大的中继节点。算法的详细步骤如下: 步骤1:在初始阶段,每个用户节点将自己的中断概率需求以及最大发送功率广播给每个中继节点。中继节点依据其感知到的信道增益和它的最大发送功率利用定理1计算各协作链路的最小传输功率,并将最小传输功率以权重Qij的形式通知相应的用户节点。 步骤2:在t时刻,用户节点i向中继节点广播其对所有中继的出价priceij( )t。每个中继节点j收到用户广播来的出价信息后,选择最高出价作为自己的价格,然后将自己的价格price*j( ) t广播给所有用户节点。用户节点i根据收到的广播信息和本地存储的中继信息相比较,然后更新本地存储的所有中继j的价格: 所有用户节点迭代执行步骤二到步骤四,直到整个网络系统达到均衡状态。所谓的均衡状态是指每个用户节点最终选择的中继节点都是使其效益最大的中继节点,即满足 由于用户节点想要让中继节点为其服务时,需要向中继节点出价,因此当多个用户节点都选择同一个中继节点时,这些用户节点需要互相竞价。但是由于用户节点可能仅请求将该中继节点分配给它们却不增加出价,这将导致竞价行为无限进行下去。为了避免这种情况发生,规定用户节点每次出价都必须至少增加ε,所以,如果最终的分配满足 则也认为这是处于均衡状态。 当迭代完成后,整个网络系统处于均衡状态,此时用户节点所选择的中继节点可以使整个无线网络的总传输功率最小。 3.3算法分析 在上述算法中,假设经过有限次迭代,网络系统处于均衡时,第i个用户节点所选择的中继为α (i),第j个中继的价格为price*j,则该算法的时间复杂度及最终分配所对应的总传输功率和最优总传输的差值可分别由定理2和定理3得出。 定理2对于一个具有N个用户节点,M个中继节点的无线网络,当算法迭代完成后,该算法的运行时间为 证明在上述算法中,如果一个中继节点在k次竞价中均被某一个用户节点选为最优中继,那么它的价格至少增加kε。因此,当k足够大时,该中继和那些没有收到任何出价的中继相比将会降低用户节点的收益。当每个中继至少收到一个出价,该算法将会结束。对于初始价格为0的情况,每个中继的总迭代次数不会超过。如果每次迭代只有一个用户出价,总迭代数不会超过的N倍。一次出价过程包含O(M)次 定理3对于N个用户节点的网络,当ε>0时,最终得到的总传输功率和最优的总传输功率差值DP∈(0,Nε]。 证明当迭代完成后,每个用户节点所选择的中继均满足公式(10),将N个式子相加可得 即 根据权重和链路功率的对应关系可知最终得到的总传输功率和最优的总传输功率差值DP∈(0,Nε]。 从下文仿真结果中可以看出,本文的算法经过数次迭代后可以很快达到收敛状态。对于一些对功率要求不严格的网络环境,可以进一步增大ε的取值,以加快收敛速度。另外,为了减小网络开销,本文的算法还可以通过集中式实现。首先用户节点将中断概率需求和最大发送功率发送给中继节点,然后中继节点计算出各个链路的权重并将权重和中继的价格发送给目的节点。最后,目的节点根据这些信息在本地构建出整个网络的虚拟拓扑结构,通过迭代执行更新,加价操作得出最优的分配方案。集中式实现虽然降低了网络开销,但是要求目的节点具有一定的计算能力,同时能够负担较大的功耗。 本文考虑一个具有N个用户节点,M个中继节点和一个目的节点的多用户多中继无线网络。所有的节点分布在一个500 m×500 m的区域,假设目的节点位于(250 m,250 m)处,中继节点随机分布在以(250 m,250 m)为圆心,内圆半径50 m,外圆半径100m的圆环中,用户节点随机分布在以(250 m,250 m)为圆心,内圆半径100 m,外圆半径250 m的圆环中。假设用户节点和中继节点以及中继节点和目的节点之间的路径增益gi,j和gj,D是和它们之间的距离有关的值,其中。所有用户节点的最大发送功率为0.5 W,所有中继节点的噪声功率为0.1 μW,最大发送功率为1 W。另外,假设每条链路的中断概率阈值为0.001,信噪比阈值为0.001。为了验证该分布式拍卖算法的性能,本文进行了大量仿真实验。本文首先将分布式拍卖算法与匈牙利算法[19]进行对比,然后将传统网络环境下(用户节点和中继节点的发送功率是相等的)分布式拍卖算法得出的系统总功率与考虑链路最小传输功率时的系统总功率进行对比,下面是实验的结果和分析。 图2是用户节点数目小于中继节点数目时(假设用户节点数目比中继节点数目少10个),本文所述算法和匈牙利算法迭代次数的对比图。其中,横坐标为用户节点数目,纵坐标为算法迭代次数。 图2 迭代次数对比(N 从图2可以看出,无论ε=0.001还是ε=0.01,分布式拍卖算法的迭代次数明显要小于匈牙利算法。随着用户数目的增加,匈牙利算法的迭代次数增加的较快,而同等情况下,分布式拍卖算法的迭代次数变化比较平缓。因此,分布式拍卖算法受网络规模增大的影响较小。另外,随着用户节点数目的增加,算法的迭代次数并不是单调增加。这是因为算法的迭代次数除了和用户节点数目相关,还与每条链路的传输功率有关。 图3是当中继节点数目为固定值(假设为110个)时,本文所述算法与匈牙利算法迭代次数对比图。其中,横坐标为用户节点数目,纵坐标为迭代次数。从图中可以看出,当中继节点数目固定时,本文所述算法的迭代次数要远小于匈牙利算法,并且随着用户数目的增加,迭代次数增幅很小。因此,本算法对于用户节点数目小于中继节点数目的网络系统,能够迅速收敛,快速找到合适的中继节点。 图3 中继节点数目固定时迭代次数对比图 图4是当ε=0.001时和ε=0.01时,分布式拍卖算法得出的系统总功率和匈牙利算法得出的系统总功率的对比图。其中,横坐标为用户节点数目(假设用户节点数目比中继节点数目少10个),纵坐标为最终传输功率。从图4可以看出,分布式拍卖算法得出系统总功率曲线与匈牙利算法得出的系统总功率曲线基本重合,而且随着ε的减小,两者的误差会更小。根据图2~图4可以发现,增大ε的值不仅会加快算法的收敛速度,也会增大最终分配的误差,但是这种误差比较小。因此,当对功率要求不是十分严格时,可以适当增大ε的取值以加快网络的收敛。 图4 分布式拍卖算法与匈牙利算法的最终总功率 在传统的中继选择方案中,用户节点i和中继节点j的发送功率一般是相等的,而本算法则是令节点根据信道中断概率选择最小发送功率。根据定理1的证明[11],当Oij=β时,用户节点和中继节点的发送功率相同(pi=pj),此时节点的发送功率不一定是满足链路中断概率的最小发送概率。下面将对比这种情况下的系统最优总功率与本文中考虑链路最小传输功率时的系统最优总功率。 图5是当用户节点i和中继节点j使用相同的发送功率时的系统总传输功率与本文所述算法对应的系统总传输功率的对比图。其中,横坐标为用户节点的数目(假设中继节点数目固定为110),纵坐标为最终分配对应的总功率。从图中可以看出,本文算法得出的最终总传输功率与匈牙利算法的最终总传输功率基本一致,而在传统中继选择方案中,由于没有使用链路的最小传输功率,因而得到的总传输功率和最优结果有一定差距。 图5 分布式拍卖算法在传统中继选择方案和考虑链路最小传输功率时的系统总功率对比 本文首先针对存在瑞利衰落的多用户多中继无线网络,根据各用户的最小中断概率要求得到所有用户节点和中继节点的最小发送功率。其次,用户节点通过和中继节点交换信息,使用分布式拍卖算法独立的选择中继节点。最终所有用户节点得到合适的中继节点,该分配可以使整个无线网络系统的总传输功率最小。 实验结果显示,分布式拍卖算法可以让用户节点在仅使用本地信息的情况下独立选择中继节点。尤其是在用户节点数和中继节点数不等时,分布式拍卖算法可以使用较匈牙利算法更少的迭代次数选择合适的中继节点。另外,使用分布式算法不仅可以避免匈牙利算法中单个节点功率消耗过大的情况,还能够充分利用网络资源,延长网络寿命。本文的分析结果可以为网络架构提供重要的参考。 参考文献: [1]Yang S,Sheng Z,Mccann J,et al. Distributed Stochastic Cross-Layer Optimization for Multi-Hop Wireless Networks with Cooper⁃ative Communications[J]. IEEE Transactions on Mobile Comput⁃ing,2014,13(10):2269-2282. [2]Mo Z,Su W,Batalama S,et al. Linear-Mapping Based Coopera⁃tive Relaying Protocol Design with Optimum Power and Time Allo⁃cation[C]//Proc of the 2014 IEEE International Conference on Communications. Sydney,Australia:2014,4495-4500. [3]Soliman S S,Beaulieu N C. Exact Analysis of Dual-Hop AF Maxi⁃mum End-to-End SNR Relay Selection[J]. IEEE Transactions on Communications,2012,60(8):2135-2145. [4]Bansal A,Bhatnagar M R,Hjorungnes A,et al. Low-Complexity Decoding in DF MIMO Relaying System[J]. IEEE Transactions on Vehicular Technology,2013,62(3):1123-1137. [5]Hasan Z,Bhargava V K. Relay Selection for OFDM Wireless Sys⁃tems under Asymmetric Information:A Contract-theory Based Ap⁃proach[J]. IEEE Transactions on Wireless Communications,2013,12(8):3824-3837. [6]Deng M Z K,Cao C. Relay Selection in Wireless Cooperative Net⁃works Using Decode-and-Forward Transmission[C]//Proc of the 2013 IEEE International Conference on Signal Processing,Com⁃munication and Computing. KunMing,China:2013,1-5. [7]Zhang X L,Ji H,Li Y,et al. Energy Efficient Transmission in Re⁃lay-Based Cooperative Networks Using Auction Game[C]//Proc of the 2013 IEEE Wireless Communications and Networking Confer⁃ence. Shanghai,China:2013,1581-1585. [8]Liu E W,Zhang Q Q,Leung K K. Relay-Assisted Transmission with Fairness Constraint for Cellular Networks[J]. IEEE Transac⁃tions on Mobile Computing,2012,11(2):230-239. [9]Amarasuriya G,Ardakani M,Tellambura C. Adaptive Multiple Re⁃lay Selection Scheme for Cooperative Wireless Networks[C]// Proc of the 2010 IEEE Wireless Communications and Networking Conference. Sydney,Australia:2010:1-6. [10]Atapattu S,Jing Y D,Jiang H,et al. Relay Selection Schemes and Performance Analysis Approximations for Two-Way Networks[J]. IEEE Transactions on Communications,2013,61(3):987-998. [11]Qian L P,Wu Y,Chen Q Z. Transmit Power Minimization for Out⁃age-Constrained Relay Selection over Rayleigh-Fading Channels [J]. IEEE Communications Letters,2014,18(8):1383-1386. [12]孙立悦,赵晓晖,虢明.基于中断概率的协作通信中继选择与功率分配算法[J].通信学报,2013,34(10):84-91. [13]叶帆,邱玲.延时信道信息下一种新AF中继选择算法[J].中国科学院大学学报,2014,31(2):243-248. [14]张娜,陈曙.无线局域网MAC层协作通信改进方案[J].传感技术学报,2012,25(2):283-288. [15]刘顺兰,徐光建.一种改进的Two-Way中继协作系统下的节点选取和功率分配策略[J].传感技术学报,2012,25(3):388-401. [16]Upadhyay M A,Mehta V J,Kothari D K. Power Minimization Al⁃gorithm in Multi Source Multi Relay Cooperative Wireless Network [C]//Proc of the Nirma- University International Conference on Engineering. Ahmedabad,India:2012:1-4. [17]Lin K Y,Liu K H. Green Cooperative Relaying in Multi-Source Wireless Networks with High Throughput and Fairness Provision⁃ing[C]//Proc of the Annual Summit and Conference of the Asia-Pacific Signal and Information Processing Association. Kaohsi⁃ung,Taiwan:2013:1-7. [18]曹傧,段海霞,朱德利,等.协作通信系统中能效优化的中继分配算法[J].电子科技大学学报,2014,5(43):807-812. [19]Kuhn H W. The Hungarian Method for The Assignment Problem [J]. Naval Research Logistics Quarterly,1955,2(1-2):83-97. 武航(1989-),男,浙江工业大学在读硕士研究生,主要研究方向无线网络与通信,wuzjut@163.com; 陈庆章(1955-),男,浙江工业大学教授,博士,博士生导师,主要研究方向为传感网络、物联网、计算机网络及其应用、数据挖掘,qzchen@zjut.edu.cn; 钱丽萍(1981-),女,浙江工业大学副教授,博士,主要研究方向为无线网络(包括物联网、无线传感网络)资源优化分配理论与算法、认知无线电网络、智能电网,lpqian@zjut.edu.cn; 卢为党(1984-),男,浙江工业大学讲师,博士,主要研究方向为无线网络资源优化分配、认知无线电网络,luweid@zjut. edu.cn。 An Distributed Deployment Algorithm in Mobile Heterogeneous Networks* QIN Ningning1,2*,YU Yinghua1,WU Deen1 Abstract:According to the maximum coverage problem of heterogeneous mobile sensor networks,a distributed de⁃ployment algorithm is proposed. By updating the target division subintervals based on the coordinates and sensing ranges of different nodes,the algorithm makes the node in every subinterval determine its velocity vector,which is related with the current location and remaining energy of the node and its delaunay neighbor nodes. Taking advan⁃tage of the mobility,the nodes would most likely to cover the target area. The simulation results show that this algo⁃rithm can improve the coverage rate and coordination speed of the network,as well as enhancing the balance of the residual energy of different nodes. Key words:sensor networks;maximum coverage;target division subinterval;velocity vector;residual energy doi:EEACC:6150P10.3969/j.issn.1004-1699.2016.01.017 收稿日期:2015-09-06修改日期:2015-10-10 中图分类号:TN92 文献标识码:A 文章编号:1004-1699(2016)01-0088-07 项目来源:国家自然科学基金项目(61379122,61379023,61402416);浙江省自然科学基金项目(LR16F010003,LQ15F010003)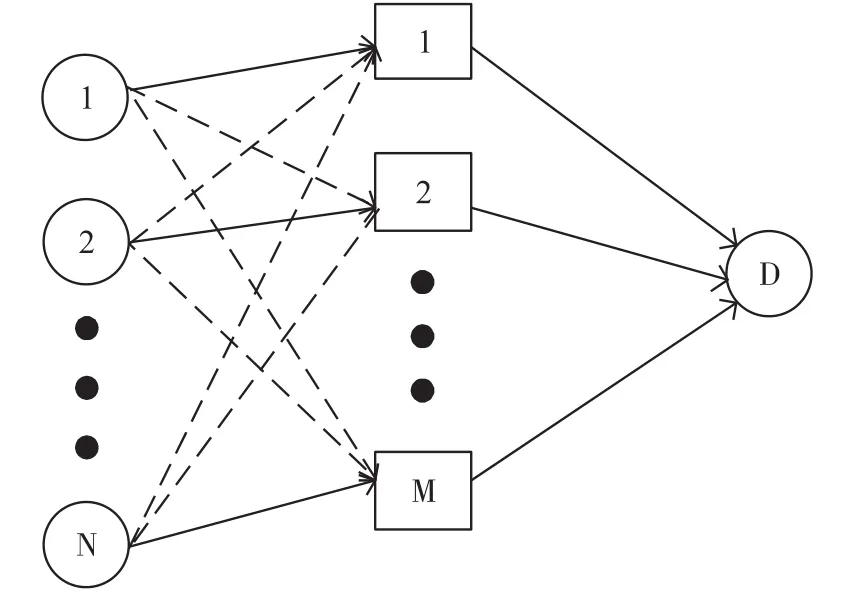
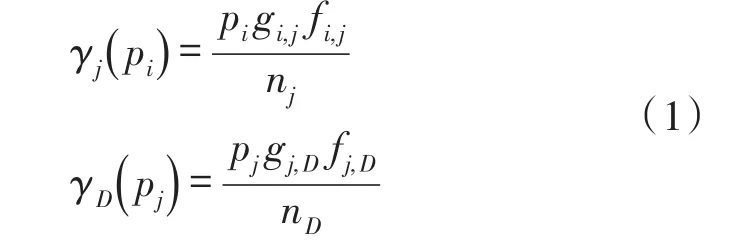
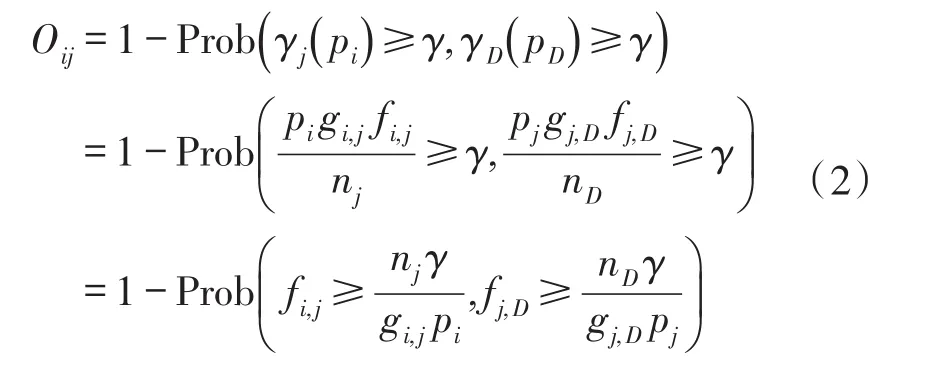
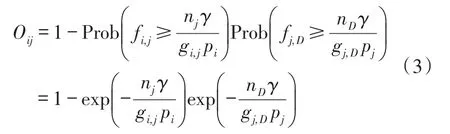
2 问题建模
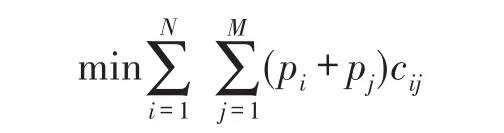
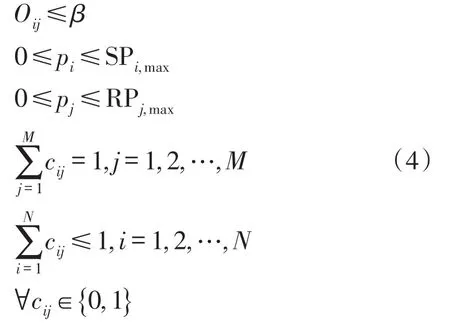
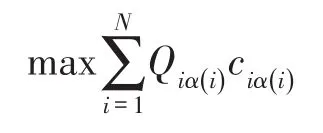
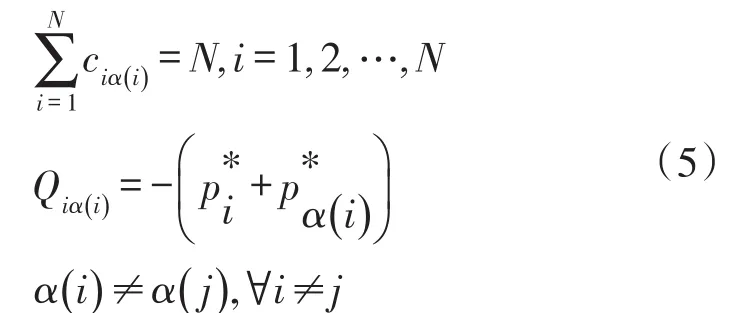
3 算法
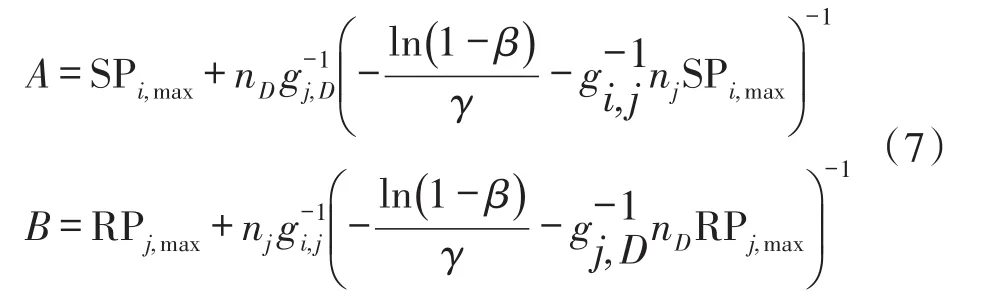
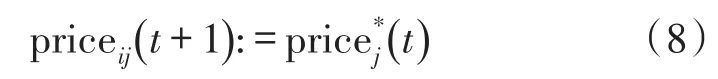
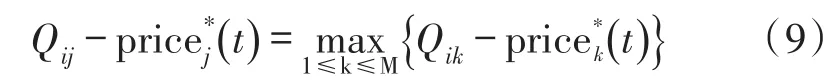

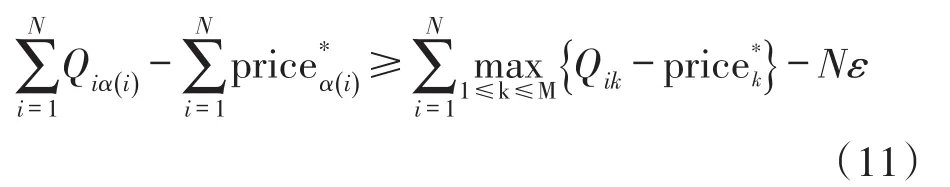

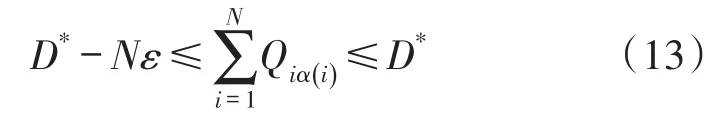
4 实验结果与分析
5 结论




(1.School of Internet of Things Engineering,Jiangnan University,Wuxi Jiangsu 214122,China;2.Key Laboratory of Advanced Process Control for Light Industry Ministry of Education,Jiangnan University,Wuxi Jiangsu 214122,China)

