电容式微加速度计的刻度温漂的半解析模型*

何江波，谢　进*，何晓平，杜连明，周　吴（.西南交通大学机械工程学院，成都600；.中国工程物理研究院电子工程研究所，四川绵阳6900；.电子科技大学机械电子工程学院，成都67）



电容式微加速度计的刻度温漂的半解析模型*

何江波1，谢进1*，何晓平2，杜连明2，周吴3
（1.西南交通大学机械工程学院，成都610031；2.中国工程物理研究院电子工程研究所，四川绵阳621900；3.电子科技大学机械电子工程学院，成都611731）

摘要：针对电容式微加速度计的刻度温漂，根据微加速度计的检测原理及热变形的分析结果，建立了刻度温漂的半解析模型，并在此基础上分析了刻度温漂的主要影响因素。分析结果表明，刻度温漂由两部分组成，第一部分主要由单晶硅的弹性模量的温度系数决定，可以通过高掺杂降低；第二部分由微加速度计的热变形引起，它的大小与封装胶的弹性模量、梳齿的宽度、大电容间隙与小电容间隙的比值以及固定梳齿锚点的位置相关；第一部分和第二部分分别是正数和负数，因此相互补偿。基于MEMS体硅微加工工艺，制造了微加速度计的实验样品，刻度温漂的测量结果验证了理论分析结果的正确性。

关键词：电容式微加速度计；刻度温漂；半解析模型；弹性模量的温度系数；封装效应；MEMS

电容式微加速度计是一种基于微机电系统（MEMS）技术的加速度传感器。电容式微加速度计的温漂包括零位温漂和刻度温漂两个参数，分别表征了零位和刻度的温度敏感性。温漂是影响测量精度的关键因素之一，特别是当电容式微加速度计应用于惯性导航系统时，温漂引起的加速度测量误差经过二次积分后会严重影响导航系统的定位精度［1］。

电容式微加速度计的温漂研究工作涉及降低措施和理论研究两方面。温漂降低措施包括恒温控制、温度补偿和隔离封装热应力等。李童杰［2］等提出的自恒温控制方案将零位温漂由2.1 mg/℃减小到0.2 mg/℃。郑长勇［3］等提出的基于三维曲面拟合的温度补偿法将零位温漂降低了一个数量级。Zwahlen P［4］等使用较软的封装胶粘接芯片，从而隔离了电容式微加速度计的封装热应力。Schröder S［5］等利用金属引线悬浮支撑电容式微加速度计的芯片，从而隔离了封装热应力。对于零位温漂，目前已有相关的理论研究。代刚［6］等运用有限元方法研究了芯片和检测电路的发热引起的零位温漂。Zhang X［7］等运用有限元方法研究了封装引起的芯片翘曲及其对零位温漂的影响。周铭［8］等基于缩减刚度矩阵的层合板模型研究了电容式微加速度计的检测电容的温度特性及其导致的零位温漂。Dai G［9］等的多物理场有限元仿真结果表明，制造误差以及硅与玻璃的热膨胀系数失陪是引起零位温漂的主要原因。对于刻度温漂的理论研究，目前还未见公开报道，这不利于设计出刻度温漂较低的电容式微加速度计。

本文根据电容式微加速度计的检测原理及热变形的分析结果，建立刻度温漂的半解析模型，并分析影响刻度温漂的主要因素。

1　检测原理

本文研究的微加速度计如图1所示，芯片的制造工艺主要包括高鹏扩散掺杂、体硅深反应离子刻蚀以及硅−玻璃阳极键合等，芯片通过环氧树脂胶粘接于陶瓷管壳上以进行封装。在芯片结构中，硅敏感结构的材料为高硼掺杂的单晶硅，衬底材料为Pyrex 7740玻璃。硅敏感结构的4根弹性折叠梁构成了微加速度计的弹簧，弹簧刚度可以根据折叠梁在敏感方向的弯曲变形进行计算。位于质量块上的可动梳齿与位于锚点上的固定梳齿构成了微加速度计的检测电容。微加速度计采用差分电容检测原理，如图2所示。惯性力使质量块发生移动，从而改变CA与CB的电容间隙，然后固定梳齿上的交流信号感应CA与CB的差值的变化，进而在质量块上产生测量信号，再经调制放大得到微加速度计的输出电压：

式中，Vout为输出电压，M为由电路参数决定的系数。

2　热变形分析

在MEMS结构中，硅敏感结构的体积通常远小于衬底的体积，硅敏感结构对衬底的热变形几乎没有影响，这使得硅敏感结构可以被处理为单独的模块，而衬底上表面的热变形是硅敏感结构模块的输入［10］。玻璃衬底粘接于陶瓷上，因此玻璃、环氧树脂和陶瓷构成复合结构，本文称为封装模块。微加速度计的热变形分析过程为：首先分析封装模块的热变形，然后提取衬底上表面的热变形，并将其作为硅敏感结构模块的输入，最后分析硅敏感结构模块的热变形。

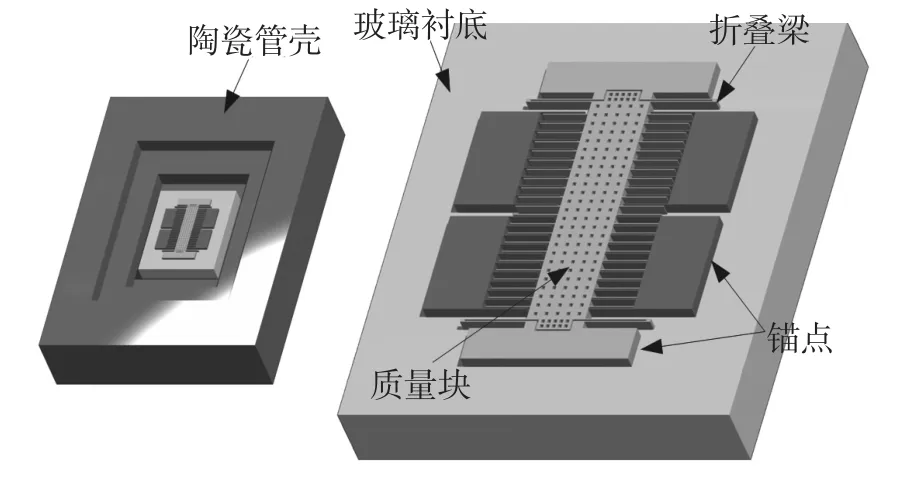
图1　微加速度计的结构示意图

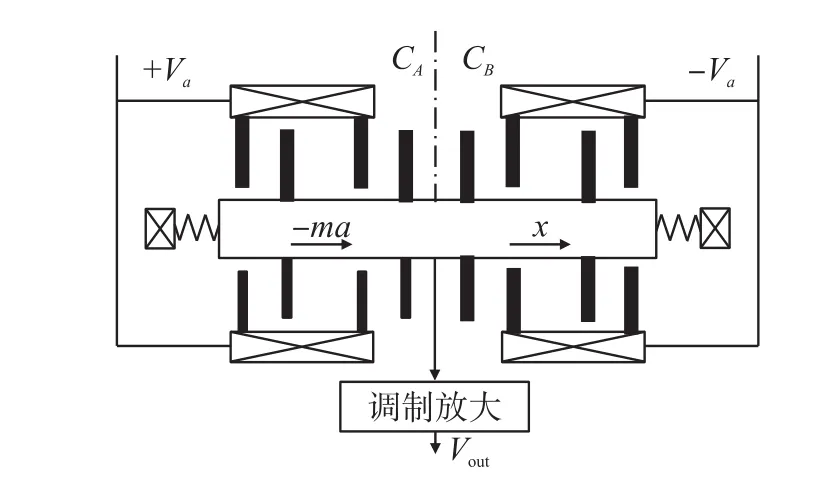
图2　微加速度计的检测原理示意图

2.1封装模块

封装模块是复合结构，其热变形很难得到解析公式，本文采用有限元软件Comsol Multiphysics［11］分析封装模块的热变形。环氧树脂的弹性模量会随温度升高而减小，特别是在玻璃化温度附近，但是在玻璃化温度之前，弹性模量受温度的影响较小［12］。由于玻璃化会显著降低环氧树脂的弹性模量、热膨胀系数、耐化学性、尺寸稳定性等属性，因此环氧树脂的最高工作温度通常低于玻璃化温度［13］。根据以上分析，在不大的温度变化范围之内，环氧树脂的弹性模量可以近似处理为常数。许多研究文献在分析MEMS器件的封装热应力时均采用了这种近似处理方法［8，14］，这可以简化分析过程。同理，本文在分析微加速度计的热变形时将环氧树脂的弹性模量设定为常数，环氧树脂以及其它材料的参数均取自室温条件（20℃），材料的室温弹性模量、泊松比和热膨胀系数（CTE）列于表1中。封装模块的有限元模型如图3所示，有限元模型采用了对称模型以降低模型自由度，模型的温度变化量为-40℃。

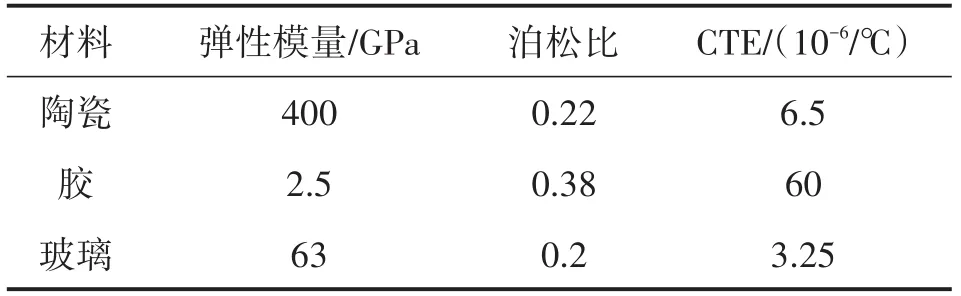
表1　室温条件下的材料参数

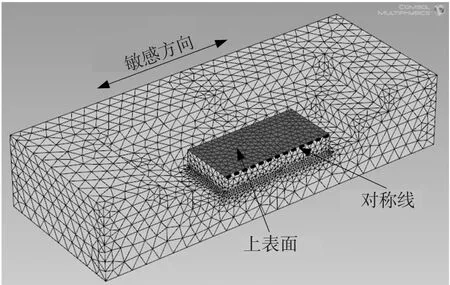
图3　封装模块的有限元模型

由有限元分析得到的衬底上表面的敏感方向位移如图4所示。

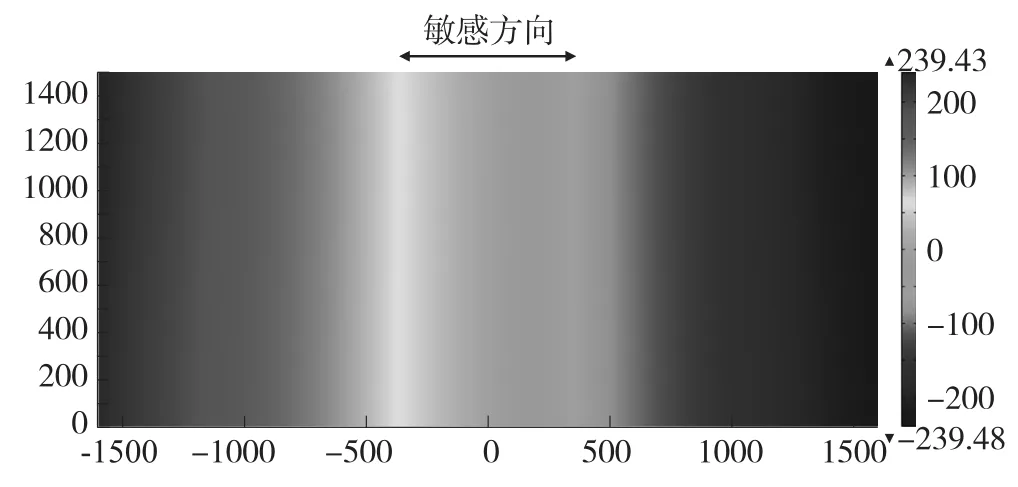
图4　玻璃上表面的敏感方向位移

从图4可以看到，敏感方向位移基本不随纵坐标变化，换言之，可以利用衬底上表面上的任意一条平行于敏感方向的直线来表征整个平面的敏感方向位移。对于如图3所示的对称线，其敏感方向位移如图5所示。

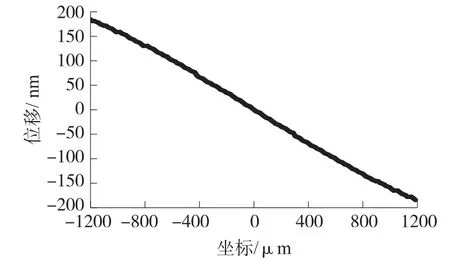
图5　对称线上的敏感方向位移

从图5可以看到，位移具有非常好的线性性质，尤其是在区间［-1 000 μm，1 000 μm］内。为了方便后文分析，对位移曲线进行线性拟合可以得到：

式中，αeq称为玻璃上表面的等效热膨胀系数，通过计算其值约为4.3×10-6/℃。由于陶瓷的热膨胀系数大于玻璃的热膨胀系数，即陶瓷会加剧玻璃的热变形，因此αeq肯定会大于玻璃的热膨胀系数。

2.2硅敏感结构模块

本节通过分析硅敏感结构的热变形计算电容间隙的变化量。固定梳齿与锚点直接相连，因此固定梳齿的位移由锚点的热变形决定，而锚点键合在衬底上，其体积远小于衬底，因此锚点的热变形由衬底上表面的热变形决定。可动梳齿的位移由质量块的热变形决定，而质量块的热变形由单晶硅的热膨胀系数决定，因为非常柔软的折叠梁隔离了锚点对质量块热变形的影响。根据梳齿的几何位置，梳齿的位移可以表示为：

式中，lm_i、lm_i+1和lf_i代表梳齿到结构中心线的距离，如图6所示，下标A和B分别代表电容CA和CB，m 和f分别代表可动梳齿和固定梳齿，i和i+1代表梳齿的编号。根据梳齿的位移，电容间隙的变化量以及平均变化量可以表示为：

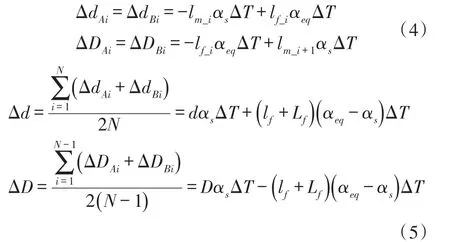
式中，αs为单晶硅的热膨胀系数，d和D为温度变化之前的小电容间隙和大电容间隙，Lf为固定梳齿锚点在敏感方向的长度的一半，lf为固定梳齿锚点到结构中心线的距离，N为单个梳齿结构中的梳齿对数。

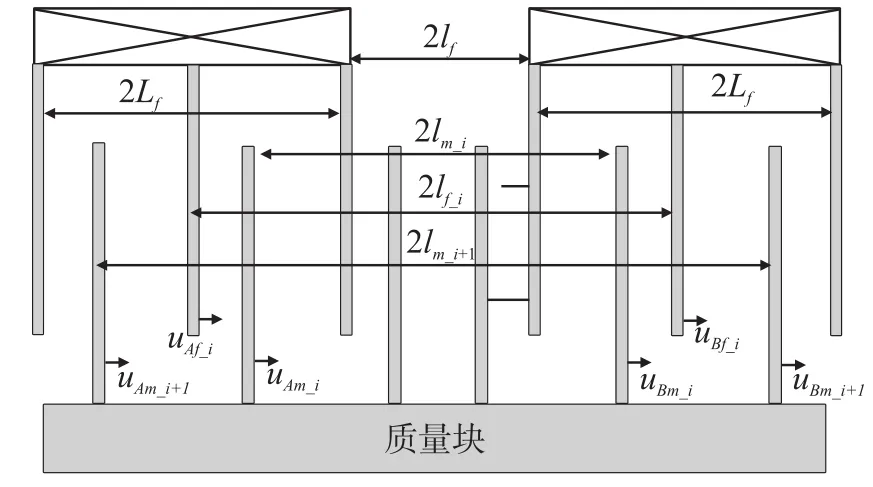
图6　梳齿位移的分析示意图

3　刻度温漂模型及分析

3.1刻度温漂模型

温度变化之后，并且惯性力产生的质量块位移为x，如图2所示，则CA与CB的温度变化之后的电容间隙分别为（d+ΔdAi+x）、（D+ΔDAi-x）、（d+ΔdBi-x）和（D+ΔDBi+x）。根据电容间隙，温度变化之后的CA与CB可以分别表示为：

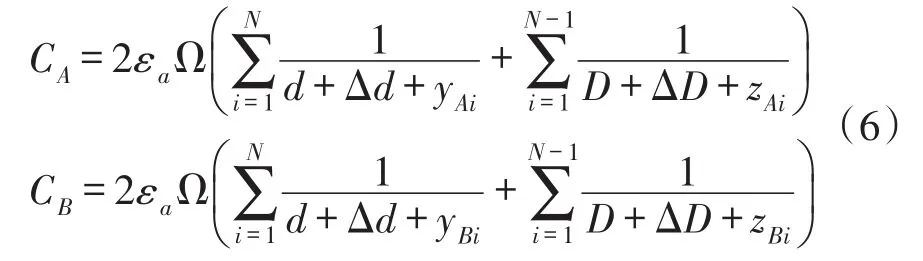
式中，yAi=ΔdAi-Δd+x，yBi=ΔdBi-Δd-x，zAi=ΔDAi-ΔD-x，zBi=ΔDBi-ΔD+x，Ω为一对梳齿的重叠面积，εa为空气的介电常数。将式（6）代入式（1）中，则Vout成为yAi，yBi，zAi和zBi的多元函数，根据多元函数的泰勒展开定理，Vout可以表示为：

式中，γ=（N-1）/N。由于N通常远大于1，因此γ近似等于1。温度变化之后，质量块位移x可以由惯性力-ma和弹簧刚度计算得到：

式中，K为温度变化之前的弹簧刚度，αK弹簧刚度的温度系数。将式（8）代入式（7）中，并将γ近似等于1可以得到：

由于刻度表示了单位输入引起的输出变化，因此由式（9）可以得到温度变化之后的刻度：

根据式（10），刻度温漂可以表示为：

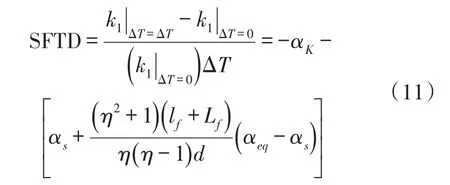
式中，η等于D/d。

3.2刻度温漂分析

由式（11）可知，刻度温漂由两部分组成，分别由弹簧刚度的温度系数和微加速度计的热变形引起。根据硅微谐振器的研究结果，刚度的温度系数等于单晶硅的弹性模量的温度系数加上单晶硅的热膨胀系数（2.6×10-6/℃），低掺杂硅的弹性模量的温度系数为-63×10-6/℃，因此低掺杂硅的刚度的温度系数约为-60.4×10-6/℃［15］。高掺杂可以降低单晶硅的弹性模量的温度系数的绝对值，例如当硼的掺杂浓度达到1020cm-3时，单晶硅的弹性模量的温度系数降低到约-20×10-6/℃［16］。对于掺杂浓度与弹性模量的温度系数之间的关系，较完整的测量数据还未见公开报道。对于本文研究的微加速度计，由于高硼扩散掺杂是其敏感结构的制造工艺之一，硼离子浓度随着结构高度变化，因此弹性模量的温度系数同样会随结构高度变化，这使得微加速度计刚度的温度系数的准确值较难计算，刚度的温度系数是大于-60.4×10-6/℃的负数。由于刻度温漂的第一部分等于刚度温度系数的相反数，因此刻度温的漂第一部分是小于60.4×10-6/℃的正数。

相关的研究表明，减小封装胶的弹性模量可以减小MEMS器件的热变形［4，14］。对于本文研究的微加速度计，封装胶的弹性模量通过αeq影响器件的热变形，进而影响刻度温漂。刻度温漂的第二部分随封装胶弹性模量的变化趋势如图7所示，当弹性模量从4.5 GPa减小到0.1 GPa时，刻度温漂第二部分的绝对值从228×10-6/℃减小到80×10-6/℃，说明减小封装胶的弹性模量可以降低刻度温漂的第二部分。

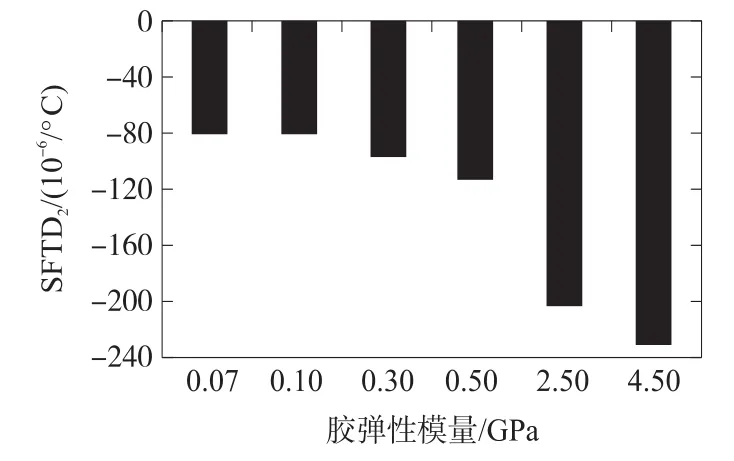
图7　SFTD2随胶弹性模量的变化

根据图8，固定梳齿锚点的半长Lf可以表示为：

式中，t为梳齿宽度。将式（12）代入式（11），刻度温漂的第2部分可以表示为：

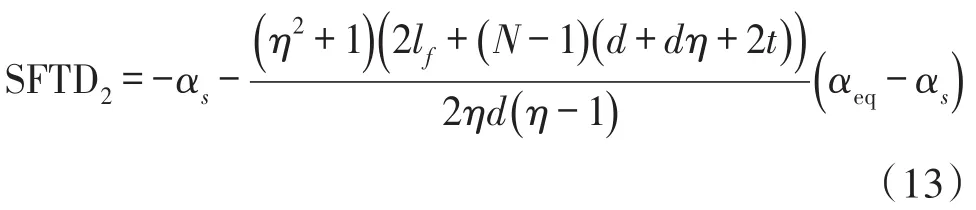
由式（13）可以得出，刻度温漂第二部分SFTD2是t和lf的线性函数，减小t和lf可以降低SFTD2。SFTD2是η的非线性函数，当η趋近于1以及∞时，SFTD2都将趋近于-∞，因此SFTD2将在某一特定η值达到极值。SFTD2随η的变化曲线如图9所示，当η等于3.9时，SFTD2达到极值−194.6×10-6/℃。在SFTD2-η函数曲线的极值点右侧，SFTD2随η的变化比较平缓。由于微加速度计的线性度会随着η的增大而显著增大［17］，因此综合考虑刻度温漂和线性度，η的设计值应取在SFTD2-η函数曲线的极值点右侧。

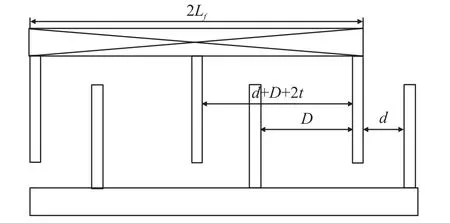
图8　梳齿结构示意图

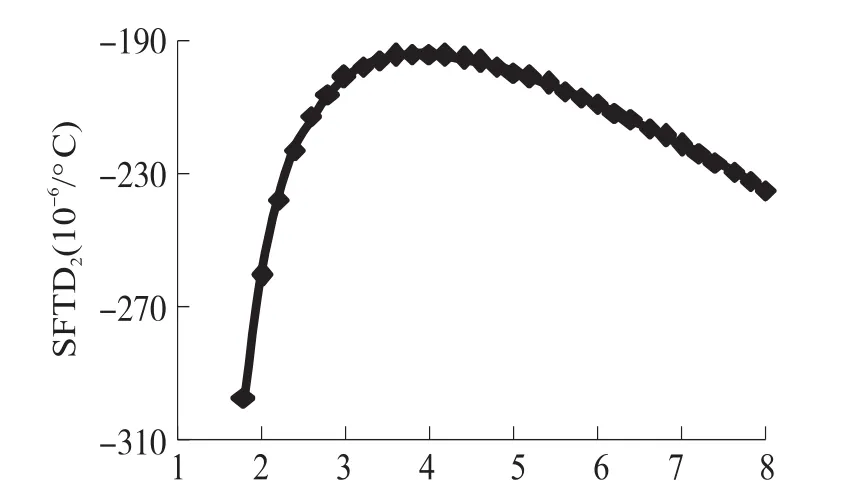
图9　SFTD2随η的变化

4　实验验证

4.1实验方法

微加速度计的制造工艺包括高鹏扩散掺杂、体硅深反应离子刻蚀以及硅-玻璃阳极键合等，微加速度计的电子扫描显微镜图（SEM图）如图10所示。

为了测量微加速度计的刻度温漂，将微加速度计及其测量电路安放于可以精确控温的温箱内，从而测量不同温度下的刻度。通过在敏感方向±1 gn翻转微加速度计可以测量得到刻度，若微加速度计在+1 gn和-1 gn状态时的输出分别为Vout（+1）和Vout（-1），则刻度可以表示为：

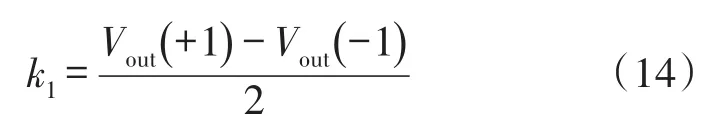
假设微加速度计的工作温度从T1变化到T2，则刻度温漂的计算式为：

式中，乘以系数106的目的是将刻度温漂的单位转化为10-6/℃。

4.2实验结果与分析

本文首先测量5个微加速度计的刻度温漂的温度曲线，测量点包括5℃、20℃、35℃、50℃、65℃、与80℃，温度曲线的测量结果如图11所示。从图中可以看出，所有温度曲线都是单调递减的，即刻度温漂为负数，与第3节的分析结果是吻合的。根据温度曲线的单调特性，刻度温漂可以由两个定点温度的刻度测量结果计算得到，本文实验的固定温度点分别为5℃与55℃，这样的测量方法可以提高实验效率，利于得到更多的实验数据。

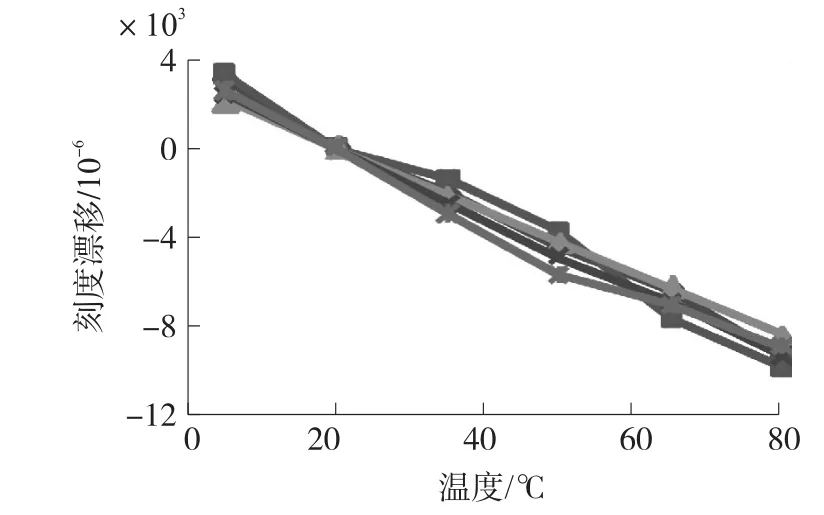
图11　刻度温漂曲线的测量结果

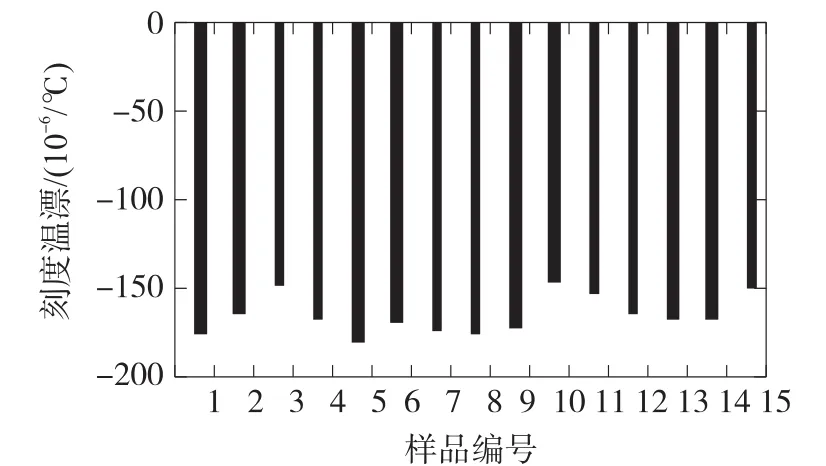
图12　刻度温漂的测量结果

图12列出了由5℃与55℃的刻度值计算得到的15个微加速度计的刻度温漂数据，数据随机分布于区间［148.2×10-6/℃，181.3×10-6/℃］内，实验数据的随机性可能是由两方面原因造成的，一是测量误差，二是制造误差的随机特性导致的微加速度计的实验样品的电容间隙不相同［9］。刻度温漂的测量结果的平均值约为-166.8×10- 6/℃，小于-139.6×10-6/℃，与第3节的研究结论是吻合的。由刻度温漂的实验测量结果以及刻度温漂第二部分的计算结果可知，刻度温漂第一部分约为33.2×10-6/℃，换言之，高硼掺杂使单晶硅的弹性模量的温度系数由-63×10-6/℃变为-35×10-6/℃。

5　结论

本文建立了电容式微加速度计的刻度温漂的半解析模型，并分析了影响刻度温漂的主要因素。刻度温漂由两部分组成，并且相互补偿。第一部分主要由单晶硅弹性模量的温度系数决定，并且受到掺杂程度的影响。第二部分由微加速度计的热变形引起，大小受到封装胶的弹性模量、梳齿的宽度、电容大小间隙的比值和固定梳齿锚点的位置的影响。

本文未来的工作是对微加速度计的结构进行优化从而降低刻度温漂，特别是利用刻度温漂的第一部分和第二部分相互补偿的特性。

参考文献：

［1］Titterton D H，Weston J L. Strapdown Inertial Navigation Technol⁃ogy［M］. 2nd Edition. Stevenage：Institution of Electrical Engi⁃neers，2004：336-342.

［2］李童杰，刘云峰，董景新，等.微加速度计温度特性及敏感元件自恒温方案［J］.清华大学学报，2010，50（7）：1013-1017.

［3］郑长勇，陈军宁.一种新型MEMS加速度计温度补偿方法研究［J］.传感技术学报，2015，28（1）：39-42.

［4］Zwahlen P，Dong Y，Nguyen A，et al. Breakthrough in High Perfor⁃mance Inertial Navigation Grade Sigma-Delta MEMS Accelerome⁃ter［C］//International Conference on Position Location and Naviga⁃tion Symposium，2012：15-19.

［5］Schröder S，Nafari A，Persson K，et. al. Stress-Minimized Packag⁃ing of Inertial Sensors Using Wire Bonding［C］//17th International Conference on Solid-State Sensors，Actuators and Microsystems，2013：1962-1965.

［6］代刚，李枚，杜连明，等.微加速度计启动漂移特性研究与实验［J］.传感技术学报，2011，24（10）：1416-1421.

［7］Zhang X，Park S，Judy M W. Accurate Assessment of Packaging Stress Effects on MEMS Sensors by Measurement and Sensor-Package Interaction Simulations［J］. Journal of Microelectro-Me⁃chanical Systems，2007，16（3）：639-649.

［8］周铭，徐大诚，郭述文.硅微电容式加速度计热致封装效应的层合分析［J］.传感技术学报，2015，28（7）：953-957.

［9］Dai G，Li M，He X，et al. Thermal Drift Analysis Using a Multi⁃physics Model of Bulk Silicon MEMS Capacitive Accelerometer ［J］.Sensors and Actuators A：Physical，2011，172：369-378.

［10］Myers D R，Azevedo R G，Li C，et al. Passive Substrate Tempera⁃ture Compensation of Doubly Anchored Double- Ended Tuning Forks［J］. Journal of Microelectro-Mechanical Systems，2012，21 （6）：1321-1328.

［11］COMSOL中国. Introduction To COMSOL Multiphysics［EB/OL］. http：//cn.comsol.com/shared/downloads/IntroductionToCOMSOL⁃Multiphysics_CN_50.pdf.

［12］Polansky R，Mentlik V，Prosr P，et al. Influence of Thermal Treat⁃ment on the Glass Transition Temperature of Thermosetting Epoxy Laminate［J］. Polymer Testing，2009，28：428-436.

［13］Master Bond. How To：Optimizing the Glass Transition Tempera⁃ture［EB/OL］. http：//www.masterbond.com/techtips /how-optimiz⁃ing-glass-transition-temperature-tg.

［14］Liu J，Shi Y，Li P，et. al. Experimental Study on the Package of High- g Accelerometer［J］. Sensors and Actuators A：Physical，2012，173：1-8.

［15］Samarao A，Ayazi F. Temperature Compensation of Silicon Reso⁃nators via Degenerate Doping［J］. Journal of Microelectromechani⁃cal Systems，2012，59（1）：87-93.

［16］Ng E J，Ahn C H，Yang Y，et al. Localized，Degenerately Doped Epitaxial Silicon for Temperature Compensation of Resonant MEMS Systems［C］//17th International Conference on Solid-State Sensors，Actuators and Microsystems，2013：2419-2422.

［17］He J，Xie J，He X，et. al. Calculating Capacitance and Analyzing Nonlinearity of Microaccelerometers by Schwarz-Christoffel Map⁃ping［J］. Microsystem Technologies，2014，20（6）：195-1203.

何江波（1987-），男，博士研究生，2011年获得西南交通大学硕士学位，2011年起攻读西南交通大学博士学位，主要从事于MEMS惯性器件的结构设计、稳定性及可靠性方面的研究，chuihaol @aliyun.com；

谢进（1959-），男，教授，博士生导师，1982年毕业于西南交通大学机械工程系，主要从事于机构学、机器人及设计自动化，机构混沌边缘、混沌控制及反控制方面的研究，xj_6302@263.net。

ThêoH Analysis of Random Error Properties for FOG

XU Dongsheng1，2，LU Ming1*，JIA Changzhi2，Kang Haiying2
（1.College of Field Engineering，PLA University of Sci & Tech，Nangjing 210007，China；2.Ordnance Engineering College，Shijiazhuang 050003，China）

Abstract：Analysis of random error properties was the key of engineering development for fiber optic gyroscope （FOG）. Aimed at disadvantages of Allan variance，total variance and Thêo1，ThêoBR was given based on Thêo1 by correcting the bias between Thêo1 and Allan variance. The ThêoH was obtained by integrating Allan variance with ThêoBR. The equivalent degrees of freedom of Allan variance，total variance，Thêo1 and ThêoH were calculated and random error properties of simulation experiment and test signal were analyzed. ThêoH could solve problems of low⁃er confidence coefficient of Allan variance and bias of Thêo1，which was the best method to analyze random error properties for fiber optic gyroscope at present.

Key words：fiber optic gyroscope；random error；ThêoH variance；unbiased estimation

doi：EEACC：7230E；763010.3969/j.issn.1004-1699.2016.01.010

收稿日期：2015-07-29修改日期：20156-10-22

中图分类号：TH824.4

文献标识码：A

文章编号：1004-1699（2016）01-0045-06

项目来源：国家自然科学基金项目(51175437)