采用MEMS惯导的小口径管道内检测定位方案可行性研究*

牛小骥，旷　俭，陈起金（武汉大学卫星导航定位技术研究中心，武汉430079）



采用MEMS惯导的小口径管道内检测定位方案可行性研究*

牛小骥*，旷俭，陈起金
（武汉大学卫星导航定位技术研究中心，武汉430079）

摘要：针对小口径管线测量仪对低成本、小尺寸惯性导航定位方案的迫切需求，本文设计了一种融合了MEMS惯导、管道里程计、地面标记器以及管道运动约束的组合定位方案及其导航定位算法。基于该方案，本文以一款典型MEMS惯性器件（STIM300）为例评估了其定位精度，并对里程计、运动约束以及反向平滑算法在提高定位精度方面的贡献做了定量分析。模拟实验结果表明，里程计以及运动约束是保证系统精度的必要条件，反向平滑算法能够进一步提高定位精度；MEMS方案对长度为2 km的管道测量精度可达10-3量级，能够满足小口径管道内检测定位的精度需求。

关键词：惯性导航系统（INS）；管道测量；扩展卡尔曼滤波；反向平滑；MEMS IMU

随着我国经济和社会的快速发展，尤其是城市化进程，石油、燃气、自来水、污水和化工等行业越来越依赖庞大的地下管道网络输送服务，而这些服务的高效可靠是由管道检测、监测以及后续维护等工作来保证的［1，2］。现今主要的管道内检测方法有漏磁检测、超声检测、涡流检测、射线检测、声发射检测、电子内窥以及视频检测［3-5］。其中故障定位是管道检测的一个重要组成部分，直接决定了后续维修开挖的工程量，而定位准确性是由管道检测仪的定位能力所决定的。

目前在地下管道内检测定位应用中，一般采用高精度的战术级惯性测量单元（IMU）来测量地下管道的地理轨迹［6］。该种级别的IMU测量能力强，可以提供准确可靠的定位结果。然而，战术级IMU的尺寸过大，无法应用于小口径管道（例如10 cm或更小），其成本也过高。因此，针对小口径管道测量，不得不考虑采用小巧便宜的微机械（MEMS）惯导器件来实现管道内定位。

MEMSIMU与其他辅助信息进行组合导航可以显著提高导航定位的精度。里程计能够测量载体前进的距离，可以转换为前进速度来抑制导航定位误差的积累［7-9］。地面标记器是指坐标已知的地面标志物，可以为管道检测仪提供位置修正信息［6］。非完整性约束是根据载体运动规律（即管道测量仪在管道内只能前后运动）提出的一种虚拟观测值，提供载体坐标系下的速度辅助信息［10］。

在导航应用中，扩展卡尔曼滤波器是多传感器数据融合的一种常用算法。此外，反向平滑算法（R-T-S平滑算法）可以应用到数据后处理中，能够显著提高导航定位精度，尤其是对于低成本、低性能惯性导航系统的组合测量系统。

本文首先阐述基于MEMS惯性导航器件的管道测量方案和相应算法；然后采用模拟实验方法定量评估了其定位测量精度，并展示了各种辅助信息在导航定位过程中的作用；最后给出结论和展望。

1　MEMS惯导组合定位方案

惯性测量单元能够感知管道检测仪的运动信息，采集的数据包括3个方向的角速度以及比力（反映载体加速度），通过投影和积分等惯性导航解算（即惯导机械编排）得到位置、速度和姿态等导航信息。在管道内检测过程中，能够准确地获得管道测量仪的位置是非常重要的。当采用MEMS惯导方案时，由于MEMS本身器件误差的影响，惯性导航系统推算的位置、速度和姿态的误差会迅速累积，严重影响MEMS惯性器件的工程应用。

管道检测仪穿梭在深埋地下的管道中，使用GNSS信息辅助抑制惯导的误差积累的方案是不可能的。其它辅助信息，例如里程计、地面标志物以及运动约束，可作为替代辅助手段，有效地抑制误差的积累。R-T-S平滑算法是进一步提高导航定位精度的一种可靠且有效的算法［11］。图1给出组合导航数据融合的详细流程图。下节将详细介绍利用上述辅助信息来修正MEMS惯导，以获得最优位置估计精度的算法。

图1　数据处理流程

2　组合定位数据融合算法

2.1惯性导航初始对准

惯性导航是一种逐步递推的导航方式，准确的初始系统状态是保障导航定位精度的基本条件，包括位置、速度、姿态。管道检测仪的工作流程为：开始时，在坐标已知的起点静止一段时间（比如30 s）；然后在管道内运动采集管道信息；最后在坐标已知的终点静止一段时间（比如10 s）后结束。根据这一流程，初始位置可以用已知坐标点赋值（通过查询设计资料获取），而初始速度则直接设为零。

初始横滚角、俯仰角可以根据静止时段的IMU数据计算得到，相应的计算公式参考文献［10］。由于MEMS惯性器件的陀螺噪声水平大于地球自转的角速度，因此无法使用陀螺数据直接计算得到初始航向角。然而在初始静止时段，我们有充足的条件通过其他方法获得初始航向角，比如通过已知坐标点反算、光学对准、磁罗盘测量等。

2.2扩展卡尔曼滤波模型

卡尔曼滤波理论自从问世以来，在解决随机线性离散系统的状态或参数估计问题方面得到了广泛的应用。而基于MEMS惯导的导航系统是一个非线性连续系统，因此标准卡尔曼滤波不适用于该系统的状态或参数估计。为此可以采用扩展卡尔曼滤波，对非线性连续系统的误差状态通过局部进行线性化，实现最优估计。这里惯性导航系统的误差状态设计为位置误差δrn、速度误差δvn、姿态误差ψ、陀螺零偏δbg、加速度零偏δba，共15维如下［12］：

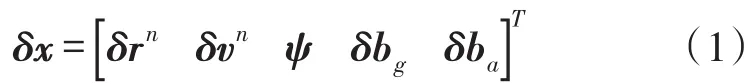
惯性导航系统的误差模型可以由下面一个连续线性随机系统的方式表示［13］：

式中，F(t)为动态矩阵，δx(t)为状态向量，G(t)为噪声输入系数矩阵，w(t)为噪声向量。

离散线性化后的惯性导航系统误差状态模型可以表示如下［10］：

式中，δxk+1为状态向量，Φk为状态转移矩阵，Gk为系统噪声驱动阵，wk为状态的噪声向量。

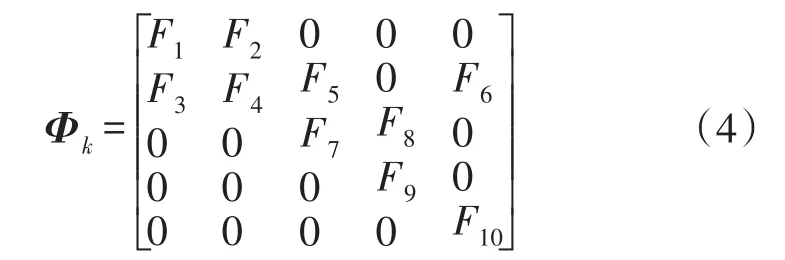
式（4）中各项参数的计算公式参考文献［10］。

在上述动态系统状态模型的基础上，还需要一个观测模型为系统状态向量x提供修正信息。这里提出的观测模型是基于地面标记器和里程计建立的。线性化观测误差模型可以表示如下：

式中，H为观测系数矩阵，v为观测噪声。其中位置观测噪声与里程计观测噪声被认为是白噪声且两者相互独立。具体设计见下一节。

2.3观测模型

地面标记器是指随着地下管线网络的走向分布地面上的标志物，且坐标信息已知，每两个地面标志器相距约2 km［6］。地面标记器会接收管道测量仪通过该处时发出的低频应答信号，从而为管道检测仪提供位置修正信息［6］。扩展卡尔曼滤波使用地面标记器的量测方程可以表示为：

式中，rIMU为惯性导航系统推算的位置，rAGM为地面标记器的位置。

里程计以累计的方式记录管道检测仪前进的总路程。根据路程与速度的转换关系可以得到管道检测仪在短时间内的速度：

式中，Δt为时间间隔，Δd为Δt内前进的路程。

非完整性约束是指载体在正常运动过程中，不会发生横向侧滑和垂向跳跃的现象，则认为载体在横向和垂向的速度为零［10］。管道检测仪的运动符合该特性，因此除了沿着管道方向速度为vwheel，横向和垂向速度都为零，即惯性导航推算的速度在管道检测仪坐标系的投影如下式所示［10］：

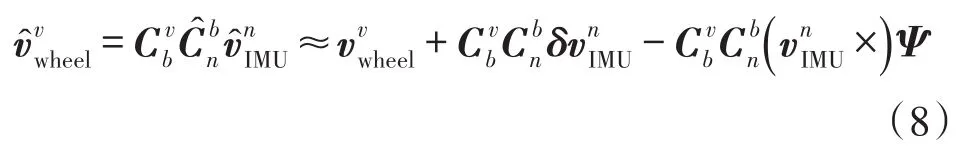
式中，上下标v，n，b分别为管道检测仪坐标系、导航坐标系、载体坐标系。Cvb为载体坐标系到管道检测仪坐标系的转换矩阵。

由里程计得到的速度观测模型如下：

式中，ev为速度观测噪声。

速度误差的量测方程表示如下［10］：

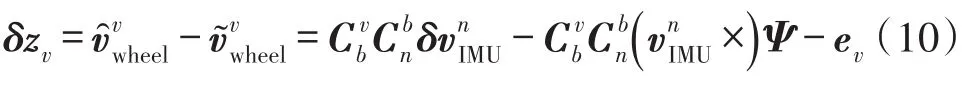
2.4扩展卡尔曼滤波更新

扩展卡尔曼滤波估计的误差是系统状态向量的最新时刻估计值，也就是说该滤波器工作形式为带有误差反馈修正的闭环。因此，每一次系统误差状态向量完成观测更新后，都要用于修正导航状态和参数，并将误差状态向量重置为零。

状态更新方程以离散的形式表示如下：

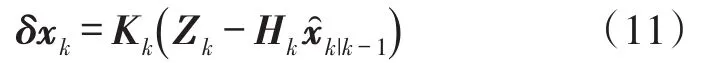
式中，Kk为滤波增益矩阵。

相应的误差协方差矩阵如下：

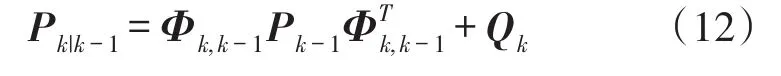
式中，P为误差状态向量的协方差矩阵，Φk，k-1为状态转移矩阵，Qk为系统噪声的协方差矩阵。卡尔曼滤波更新估计状态误差向量的协方差矩阵方式如下：

式中，Rk为观测向量的协方差矩阵。

2.5平滑算法

平滑算法是一种进一步提高导航定位精度的算法。R-T-S平滑算法是一种典型的固定区间平滑线性算法，该算法利用过去、当前以及未来的信息，能够获得比扩展卡尔曼滤波更精确的状态向量估值。R-T-S平滑算法如下所示［14］：

其中，k=N-1，N-2，…，0，N为测量值的总数。

3　模拟实验结果及数据分析

3.1模拟实验及设备性能指标

铁路轨道测量与管道测量具有非常大的相似性，区别主要是前者在地面上，后者在地下。铁路轨道测量数据可以有效模拟管道测量场景，并且能够方便地采用传统测绘手段对其坐标形状进行精密测量，获得参考真值，以评估其误差水平。

实验轨迹为东西方向的大约2 km长的直线轨道，如图2所示。

图2　运动轨迹

实验中采用了有代表性的高端MEMSIMU模块STIM300，其惯性器件的技术指标如表1所示。

表1　STIM300惯性器件参数［15］

3.2实验结果分析

数据覆盖长度为2 km的直线轨道，时间总长度为2 205 s，采样频率为200 Hz。实验过程中，系统启动后静止57 s完成系统预热以及初始对准，到达终点后静止54 s，中间有效测量时间为2 094 s。测试过程沿着直线轨道来回跑了三次，其中只在测试开始静止时刻和结束静止时刻使用地面标记对惯导进行位置修正。

数据分析中采用高精度惯性导航与高精度卫星导航组合的平滑结果为参考真值，其定位精度为厘米级别。MEMS惯导方案解算的位置与参考位置的差值作为评判标准，具体评估的数据处理方案包括：①惯性导航系统独立推算；②惯性导航系统加上非完整性约束条件，起点和终点进行位置修正；③惯性导航系统加上非完整性约束条件，同时增加里程计传感器辅助信息，起点和终点进行位置修正；④在方案3基础上，再进行平滑滤波处理。

图3~图6给出了4个解算方案的北向、东向、垂向位置误差。表1统计了方案1~方案4的位置误差，分别给出了每种方案在北向、东向、高程的位置误差的方均根值以及最大值。

从图3可以看出，惯性导航系统单独推算，位置误差迅速增大到数公里，根本无法应用于管道测量中的导航定位。图4结果表明使用非完整性约束后，惯性导航系统的位置漂移得到有效的抑制，尤其是横向（北向）和垂向。然而前向（东向）位置误差依然过大（最大值为1 545.68 m），无法满足管道检测仪的定位需求。

图3　位置误差（方案1：纯惯导）

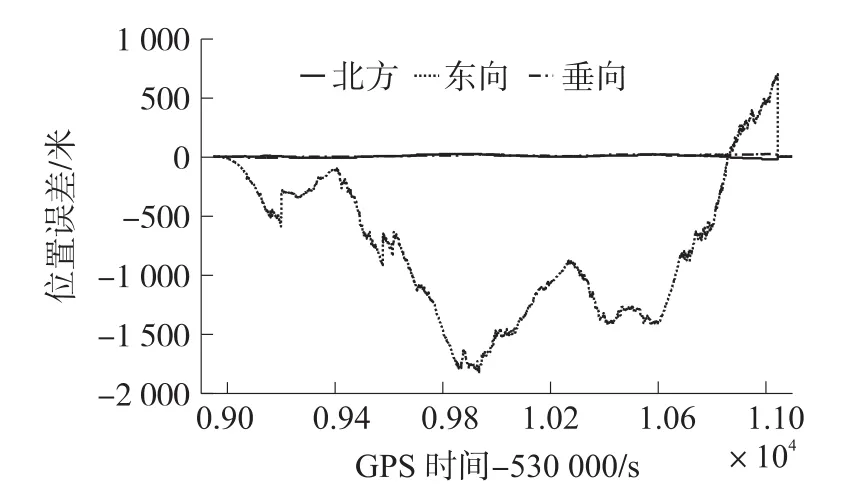
图4　位置误差（方案2：纯惯导+非完整性约束）

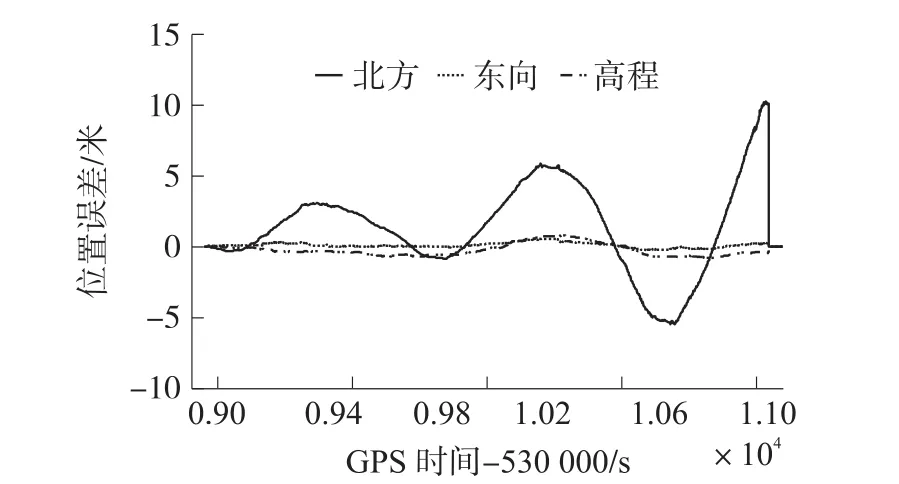
图5　位置误差（方案3：纯惯导+非完整性约束+里程计）

图6　位置误差（方案4：纯惯导+非完整性约束+里程计+平滑滤波）

图5为方案3的位置误差曲线。方案3相对于方案2增加了里程计辅助信息，有效改正了前向位置误差，从而使组合导航的位置精度有了很大程度地提升。表1的统计数值说明方案3的位置误差方均根在北向、东向、高程三个方向分别为3.37 m、0.2 m、0.49 m，最大误差为10 m，相比方案2有显著改善，已经接近管道检测仪的定位需求。

图6是方案4的定位误差结果，即在方案3的基础上进行平滑解算。比较图5和图6的误差曲线分布，平滑算法相对于滤波算法改善了导航定位结果，且位置误差分布更加均匀，系统表现更加稳定。因此在数据后处理过程中，使用平滑算法进一步提高系统的导航定位精度是非常必要的。表1的统计结果表明方案4的位置误差统计值（RMS）为亚米级，最大误差为2.24 m。本次实验数据有效测试时间为2 094 s，测量长度约为2 km，以最大误差计算，在长度为2 km的管道测量中系统测量精度优于10-3数量级，能够满足小口径管道测量的定位需求。

表1　位置误差统计值　单位：m

4　结论

本文以一款典型MEMS惯导为例，评估和验证了MEMS惯导用于小口径管道内定位的可行性。模拟实验表明，在无修正信息的条件下，MEMS惯导的位置漂移误差得不到抑制，其测量精度随时间急剧下降，无法应用实际工程中。利用里程计与非完整性约束等辅助信息可以有效地抑制惯导误差累积，将定位误差降低到米级，是MEMS惯性器件应用于管道测量仪的必要条件；R-T-S平滑算法利用所有可用信息对导航状态进行最优估计，能够进一步提高测量精度，接近亚米级水平。在长度为2 km的管道测量中MEMS惯导方案的定位精度优于10-3量级，满足实际工程中管道测量的精度需求。因此以STIM300为代表的MEMS惯性器件可以应用于小口径的管道测量仪。

下一步工作将进行STIM300的现场测试验证，考察STIM300在工程应用条件下的测量能力，并针对出现的问题进行方案和算法优化。

参考文献：

［1］Hanna P L，Napier M E，Ashkenazi V. Strapdown Inertial Survey⁃ing for Internal Pipeline Surveys［M］. Kinematic Systems in Geod⁃esy，Surveying，and Remote Sensing，Springer，1991：140-153.

［2］王良军，李强，梁菁嬿.长输管道内检测数据比对国内外现状及发展趋势［J］.油气储运，2015，34（3）：233-236.

［3］傅忠尧.油气管道内检测常用方法［J］.装备制造技术，2015 （1）：206-208.

［4］刘梦然，张国军，简泽明，等.管道内检测器声定位技术研究［J］.传感技术学报，2014（4）：500-504.

［5］韩玲娟，王强，杨其华，等.基于分布式光纤传感的水下输气管道泄漏检测与定位分析［J］.传感技术学报，2015（07）：1097-1102.

［6］李睿，冯庆善，蔡茂林，等.基于多传感器数据融合的长输埋地管道中心线测量［J］.石油学报，2014（5）：987-992.

［7］杨理践，杨洋，高松巍，等.管道地理坐标内检测的里程校正算法［J］.仪器仪表学报，2013（1）：26-31.

［8］杨理践，沈博，高松巍.基于组合导航技术的管道地理坐标定位算法［J］.沈阳工业大学学报，2014（1）：66-71.

［9］杨洋，杨理践，沈博.管道地理坐标测量误差校正方法的研究［J］.传感技术学报，2012，25（10）：1416-1421.

［10］Shin E. Estimation Techniques for Low-Cost Inertial Navigation ［J］. UCGE report，2005，20219.

［11］Gelb A. Applied Optimal Estimation［M］. MIT Press，1974.

［12］Shin E，El-Sheimy N. Accuracy Improvement of Low Cost INS/ GPS for Land Applications［M］. University of Calgary，Depart⁃ment of Geomatics Engineering，2001.

［13］Noureldin A，Karamat T B，Eberts M D，et al. Performance En⁃hancement of MEMS- Based INS/GPS Integration for Low- Cost Navigation Applications［J］. IEEE Transactions on Vehicular Technology，2009，58（3）：1077-1096.

［14］Rauch H E，Striebel C T，Tung F. Maximum Likelihood Estimates of Linear Dynamic Systems［J］.AIAAJournal.1965，3（8）：1445-1450.

［15］Sensonor. Datasheet Stim300［Z］. 4-5.

牛小骥（1973-），男，武汉大学卫星导航定位技术研究中心教授，清华大学博士毕业，加拿大卡尔加里大学博士后，SiRF公司高级研究员；目前在武汉大学卫星导航定位技术研究中心从事惯性导航（INS）和组合导航（GPS/INS）方面的研究，xjniu@whu.edu.cn；

旷俭（1990-），男，武汉大学卫星导航定位技术研究中心硕士研究生，主要研究方向为惯性测量与组合导航，kuang@whu.edu.cn。

Semi-Analytical Model for Scale Factor Thermal Drift of Capacitive Microaccelerometers*

HE Jiangbo1，XIE Jin1*，HE Xiaoping2，DU Lianming2，ZHOU Wu3
（1.School of Mechanical Engineering，Southwest Jiaotong University，Chengdu 610031，China；
2.Institute of Electronic Engineering，China Academy of Engineering Physics，Mianyang Sichuang 621900，China；3.Schoolof Mechatronics Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China）

Abstract：For the scale factor thermal drift（SFTD）of capacitive microaccelerometers，its semi-analytical model is established based on the detection principle and thermal deformation results of microaccelerometers. Then，the main factors affecting SFTD are analyzed. The results show that SFTD is composed of two parts. The first part，which is mainly determined by the temperature coefficient of elastic modulus of silicon，can be reduced by heavydoping. The second part caused by the thermal deformation has relationship with the elastic modulus of adhesives for packaging，finger width，the ratio between wide gap and narrow gap，and the location of the anchor for the fixed comb fingers. The first part and second part are positive and negative respectively，so they compensate each other. Based on the MEMS bulk silicon micromachining，experimental samples of microaccelerometers are fabricated. The testing results of SFTD verify the theoretical analysis results of SFTD.

Key words：capacitive microaccelerometers；scale factor thermal drift；semi-analytical model；temperature coeffi⁃cient of elastic modulus；packaging effect；MEMS

doi：EEACC：7320E；723010.3969/j.issn.1004-1699.2016.01.009

收稿日期：2015-08-11修改日期：2015-09-20

中图分类号：U666.1

文献标识码：A

文章编号：1004-1699（2016）01-0040-05

项目来源：国家自然科学基金项目（41404029，41174028，41304004）；中央高校基本科研业务费专项资金——武汉大学自主科研项目（学科交叉类，2042014kf0258）