快时变多用户MIMO-OFDM系统中复杂度可调的子载波分组预编码技术*

童娟娟，束　锋，2，3*，李　隽，李　蠡，王忆蒙，桂林卿，陆锦辉

（1.南京理工大学电子工程与光电技术学院，南京210094；2.东南大学移动通信国家重点实验室，南京210096；3.南京理工大学近程高速目标探测技术国防重点学科实验室，南京210094）



快时变多用户MIMO-OFDM系统中复杂度可调的子载波分组预编码技术*

童娟娟1，束锋1，2，3*，李隽1，李蠡1，王忆蒙1，桂林卿1，陆锦辉1

（1.南京理工大学电子工程与光电技术学院，南京210094；2.东南大学移动通信国家重点实验室，南京210096；3.南京理工大学近程高速目标探测技术国防重点学科实验室，南京210094）

摘要：在时变多用户MIMO-OFDM系统中，所有子载波整体预编码方案的性能优于单个子载波单独预编码方案。然而前者的复杂度是基站发射天线数J与子载波总数N乘积的函数，显著高于后者，特别NJ>1000时，复杂度极高。为了解决这个问题，我们提出了一种基于最大化信泄噪比的复杂度可调的分组子载波GS-Max-SLNR（Grouped-Subcarrier Maximum Signal-to-Leakage-and-Noise Ratio）预编码方案。此外，我们推导了组间干扰公式，该公式在给定多普勒频移和信噪比的条件下，可以根据需要选取合适的分组数。理论建模和仿真表明，通过选取合适的分组数目，提出的GS-Max-SLNR能够实现复杂度和性能的良好折中。

关键词：多输入多输出；正交频分复用；最大化信泄噪比；子载波分组；线性预编码

项目来源：国家自然科学基金项目（61271230，61472190）；中央高校基本科研业务费专项资金项目（30920130122004）；东南大学移动通信国家重点实验室开放课题项目（2013D02）

多用户宽带MIMO-OFDM系统的预编码方法是一个热点问题。主要设计方案大体可以分为两类：第1类，每个子载波单独预编码，直接将窄带系统（非OFDM）预编码方法直接运用于每个子载波，本文中称之为单子载波IS（Individual-Subcarrier）预编码方法［1-4］；第2类，所有子载波整体预编码，又称为全局预编码GP（Global-Precoding），或者空频联合编码［5-6］。GP能够充分利用多普勒频率分集和空间分集，而IS预编码只利用了空间分集增益。因此，GP的误比特BER（Bit Error Rate）性能优于IS预编码的BER性能。对于基于矩阵分解的一类线性预编码如块对角化、最大化信泄噪比等，它们的GP复杂度是O[(NJ)3]次复乘运算，例如J=8且N=128时，GP每个OFDM符号需要O[(NJ)3]≈O(109)次复乘运算，复杂度极高。因此，我们提出了一种复杂度可调的基于最大化信泄噪比的分组子载波GS-Max-SLNR（Grouped-Subcarrier Maximum Signalto-Leakage-and-oise ratio）预编码方案，旨在获得复杂度与性能的良好折中。

本文主要结构如下：第1节详细描述了提出的GS-Max-SLNR结构；第2节分析了组间干扰IGI （Inter-Group Interference）；第3节给出了仿真结果与分析；最后1节总结全文。

下文中，矩阵、向量以及标量分别用粗体大写字母、粗体小写字母和小写字母表示。运算符号⊗表示两个矩阵的Kronecker积。运算符号(·)H、(·)T和Tr(·)分别表示矩阵的共轭转置、转置和迹。In表示一个n×n的单位阵。

1　提出的复杂度可调的子载波分组预编码方案

提出的基于GS-Max-SLNR结构的多用户MI⁃MO-OFDM宽带系统模型如图1所示。该系统基站配置J副发射天线，用户k配置Mk副接收天线。如图2所示，每个用户的N个子载波被分为I组，每组分配N/I个子载波。所有用户同一组的发射信号将被映射到J副发射天线的对应组，并且与其他组相互独立。用户k第i组接收到的N/I维频域信号向量如下。

图1　提出的多用户MIMO-OFDM系统分组子载波结构

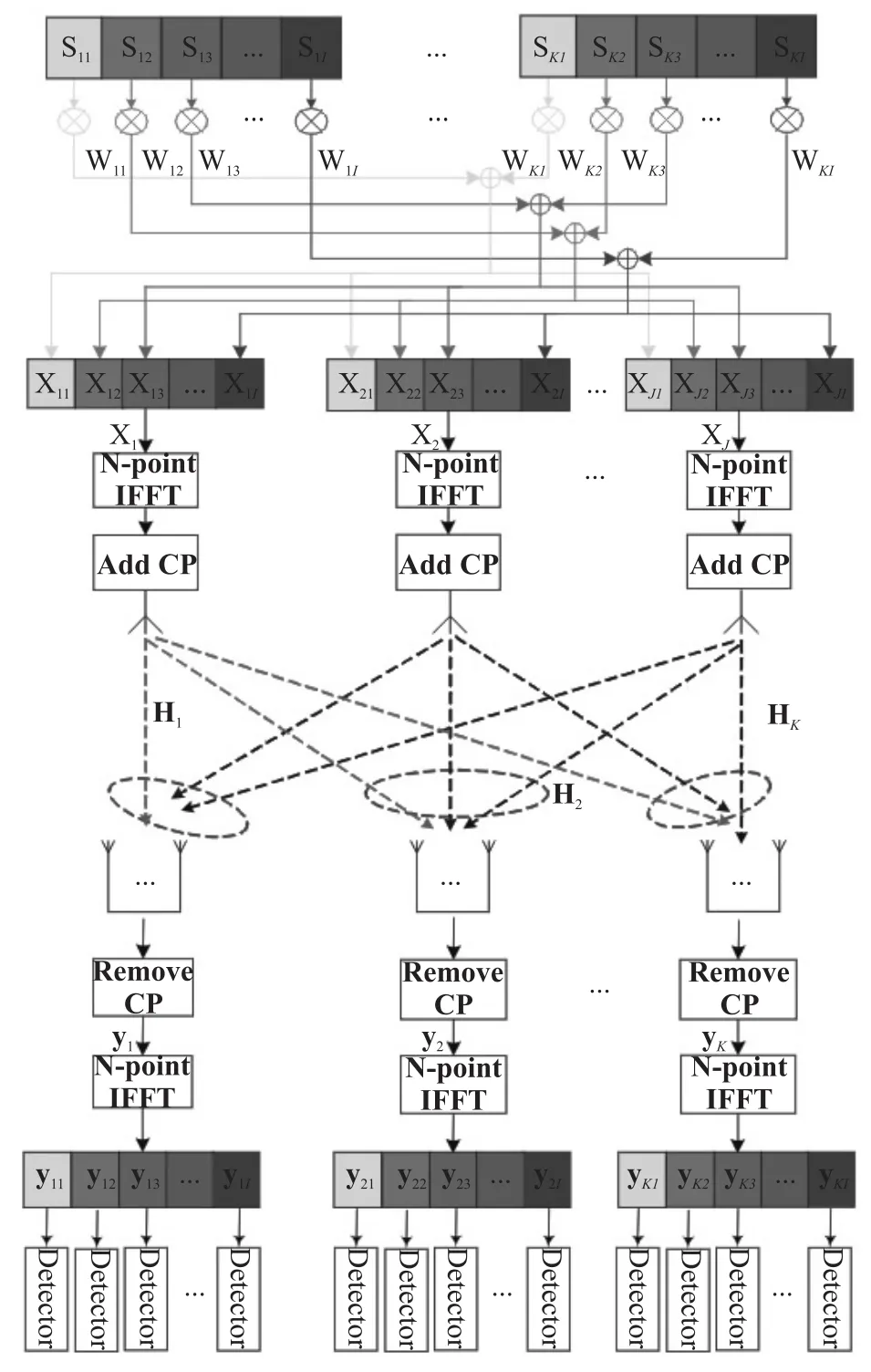
图2　提出的GS结构分组示意图

其中矩阵Wki为JN/I×N/I维的线性预编码矩阵，它将用户k的第i组信号映射到J副发射天线的第i组；sk是用户k的发射信号向量，定义ski=[sk(a)...sk(b)]T，是N/I维的用户k第i组发射信号向量，其中a=(i-1)∙N/I+1，b=i·N/I，ski归一化如下：E[skiskiH]=IM，其中M=Mk，Pt表示基站总发射功率；nki为信道的频域加性噪声向量，其每个元素服从方差为σ2ki的独立复高斯同分布，即E[nkinkiH]=σ2kiI。

信道矩阵Gk,ii′可以从整体信道矩阵中抽取得到如下

其中抽取矩阵Θi=[eN(a)...eN(b)]T，eN(n)为一个N×N维的单位矩阵第n行，与文献［5］中定义相似，Gk是基站到用户k的频域信道矩阵。

式（1）右边第1项是用户k第i组期望信号，第2项为来自其他用户第i组信号的干扰，第3项表示所有用户其他组的干扰。

基于式（1）和信息论相关理论，用户k第i组的互信息量如下：

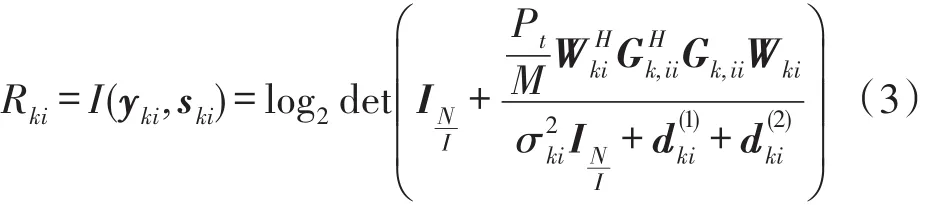
其中d(1)ki是其他用户第i组对用户k第i组的干扰，表达式如下

式中，d(2)ki是所有用户其他组对用户k第i组的干扰，表达式如下

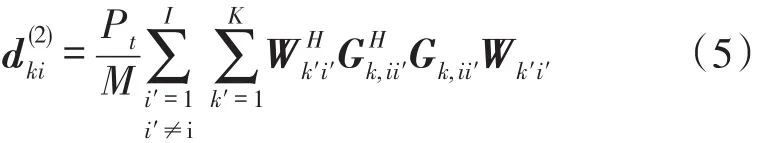
根据式（3），容易获得每用户每子载波平均和速率如下

忽略从用户k第i组到所有用户其他组泄漏的信号，根据文献［5］和文献［6］中信泄噪比的概念，用户k第i组的信泄噪比可以定义为该组到达接收机的期望信号功率与向其他用户相同组泄漏功率加噪声功率之和的比值，表达式如下

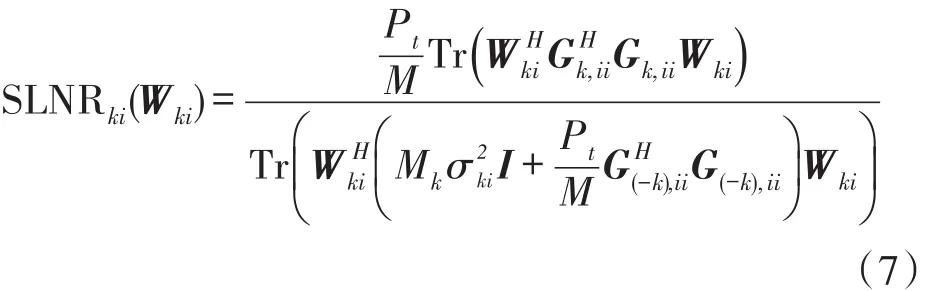
其中

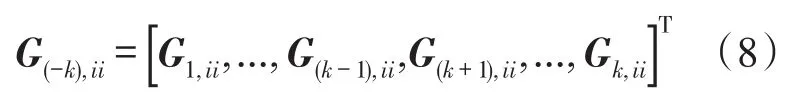
是除掉Gk,ii之外的扩展信道矩阵，且满足Tr(WWki)=1。

通过最大化SLNRki(Wki)可以得到预编码矩阵Wki，则该问题可以表示为

与文献［5］类似，我们可以直接给出该问题的解如下：

其中Bki是任意的酉矩阵，Aki的列是(MkσI+前MkN/KI个最大特征值对应的特征向量。

该算法每个OFDM符号需要O[(JN)3×I-2]次复乘，仅为文献［5］中GP-Max-SLNR算法计算复杂度O[(JN)3]的。

根据GS-Max-SLNR算法以及文献［5］给出的结论，接收端采用基于最小均方误差的检测器如下

其中，ski与yki的互相关矩阵表示为

其中，Rski是ski的自相关矩阵。yki的自相关矩阵为

2　组间干扰分析

根据文献［7］，在单输入单输出OFDM系统中单频率偏移SFO（Single Frequency Offset）引起的平均互信道干扰ICI（Inter-Channel Interference）功率可以表示为

其中Δf是SFO，PR是接收端接收到的有用功率，B表示信道带宽。在时变OFDM系统中，多普勒频谱产生的平均ICI功率可以看作是[-fd,fd]之内无限SFO产生的ICI功率之和，表示为

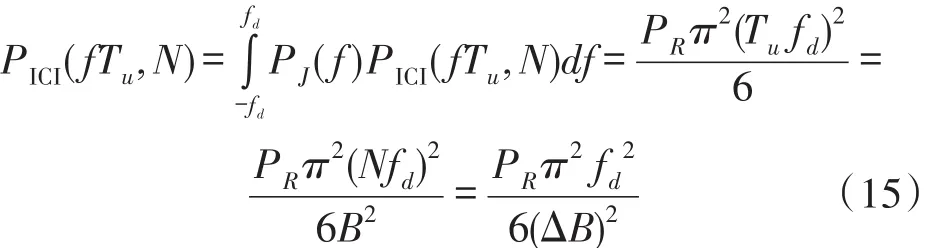
其中，PJ(f)是文献［8］中的Jake’s功率谱密度

其中ΔB是OFDM系统一个子信道的带宽。

如图2所示，我们将N个子信道分为I组，每组的N/I个子信道可以看作一个大的虚子信道，于是组成了该图右边所示新的OFDM系统，该系统中包括I个大的虚子信道，每个虚子信道的带宽为ΔBN/I，于是通过式（15）可以得到平均IGI功率如下

通过（17）式可以看出，IGI功率与I2成比例，其中I是分组总数。考虑IGI的影响，每天线每组每用户的信干噪比SINR（Signal-to-Interference and Noise Ratio）约为

其中，γ表示接收端平均信噪比。通过式（18）可以看出，减少分组数能够提高SINR的值，进而提高系统的和速率及误码率性能。该结论将在下一章的仿真中的得到验证。

3　仿真结果与分析

本文仿真采用的基带系统参数如下：发射天线数J=4，调制方式为QPSK，信道带宽WB=1 MHz，子载波数N=64，循环前缀长度为8，接收端有两个用户(K=2)且每个用户配置两副天线(Mk=2)，载波频率fc=900 MHz。归一化多普勒频移NDS（Nor⁃malized Doppler Spread）定义为fdTu，其中Tu为有用OFDM符号的长度。

图3和图4给出了当NDS≈0.5时不同分组数情况下GS-Max-SLNR的BER及和速率曲线。从图3和图4可以看出，当I≤4时，与文献［5］中的GP-Max-SLNR相比，提出的GS-Max-SLNR只损失了较少的误码率及和速率性能，但正如第2节理论分析得出的结论所述，I=4时GS-Max-SLNR的复杂度只有GP-Max-SLNR的十六分之一。

图3　不同分组情况下提出的分组预编码方案BER随信噪比变化曲线（NDS≈0.05）

图4　不同分组情况下提出的分组预编码方案和速率随信噪比变化曲线（NDS≈0.05）

进一步观察图3和图4，可以发现由于ICI的影响，在中小规模（I≤4）分组的情况下，提出的GSMax-SLNR方案与GP-Max-SLNR方案性能均优于ISMax-SLNR预编码方案。

在提出的GS-Max-SLNR方案中，一个组内的子载波是充分协作的，只存在组间干扰，当分组数为1时，提出的GS-Max-SLNR便退化为GP-Max-SLNR，而当分组数为N时，对于每一组来说都存在其他（N-1）组带来的ICI，此时提出的GS-Max-SLNR退化成IS-Max-SLNR。随着分组数I的增加，ICI的影响会逐渐恶化，当NDS较大时和速率与误码率性能都会随之恶化。于是，我们能够通过调整分组数来改变GS-Max-SLNR的复杂度，可以达到复杂度与性能的良好折中。

图5和图6展示了当NDS≈0.25时不同分组数情况下GS-Max-SLNR的BER及和速率曲线。可以看出，与NDS≈0.5的情况相比，由于其他组带来的ICI变小，不同分组情况下BER曲线与和速率曲线间的差距减小。因此，当NDS很小时，提出的GS-Max-SLNR的误码率及和速率性能与GP-Max-SLNR非常接近，同时能够显著降低计算复杂度。

图5　不同分组情况下提出的分组预编码方案BER随信噪比变化曲线（NDS≈0.25）

图6　不同分组情况下提出的分组预编码方案和速率随信噪比变化曲线（NDS≈0.25）

4　结论

本文提出了一种基于Max-SLNR的可调复杂度的子载波分组预编码方案。当分组数较小时，提出的方案的误码率及和速率性能均与文献［5］中的GP-Max-

SLNR方案性能接近，且与全局预编码方案相比，提出的GS-Max-SLNR方案能明显降低计算复杂度。更重要的是，通过改变分组数来调整复杂度，从而实现性能与复杂度之间的良好折中。此处特别指出，该分组子载波的结构能够拓展到其他线性预编码算法中去，例如最小化均方误差预编码器、奇异值分解预编码器及块对角化预编码器等［9-12］。

参考文献：

[1]Karaa H，Adve R S，Tenenbaum A J. Linear Precoding for Multius⁃er MIMO-OFDM Systems［C］//Communications，2007. ICC’07. IEEE International Conference on. IEEE，2007：2797-2802.

[2]Wang J，Xie X，Zhang Q. A Way to Reduce ICI of Multi-User MI⁃MO-OFDM System with Precoding［C］//Advanced Computer Con⁃trol，2009. ICACC’09. International Conference on. IEEE，2009：134-137.

[3]Shin Y，Kang T，Kim H. An Efficient Resource Allocation for Mul⁃tiuser MIMO-OFDM Systems with Zero-Forcing Beamformer［C］// Personal，Indoor and Mobile Radio Communications，2007. PIMRC 2007. IEEE 18th International Symposium on. IEEE，2007：1-5.

[4]Castanheira D，Silva A，Gameiro A. Linear and Nonlinear Precod⁃ing Schemes for Centralized Multicell MIMO-OFDM Systems［J］. Wireless Pers Commun，2013，72（1）：759-777.

[5]Sadek M，Aissa S. Leakage Based Precoding for Multi-User MI⁃MO-OFDM Systems［J］. IEEE Transactions on Wireless Commu⁃nications，2011，10（8）：2428-2433.

[6]Sadek M，Tarighat A，Sayed A H. A Leakage- Based Precoding Scheme for Downlink Multi- User MIMO Channels［J］. IEEE Transactions on Wireless Communications，2007，6（5）：1711-1721.

[7]Shu F，Cheng S X，Chen M，et al. A Simple Formula for ICI Caused by Single Frequency Offset in Wireless OFDM System［J］. Journal of Applied Sciences，2006，24（6）：551-554.

[8]Goldsmith A. Wireless Communications［M］. Cambridge Universi⁃ty Press，2005：63-64.

[9]Choi L，Murch R D. A Transmit Preprocessing Technique for Mul⁃tiuser MIMO Systems Using a Decomposition Approach［J］. IEEE Transactions on Wireless Communications，2004，3（1）：20-24.

[10] Spencer Q H，Swindlehurst A L，Haardt M. Zero-Forcing Methods for Downlink Spatial Multiplexing in Multiuser MIMO Channels ［J］. IEEE Transactions on Signal Processing，2004，52（2）：461-471.

[11] Liu W，Yang L，Hanzo L. SVD- Assisted Multiuser Transmitter and Multiuser Detector Design for MIMO Systems［J］. IEEE Transactions on Vehicular Technology，2009，58（2）：1016-1021.

[12] Sung H，Lee S，Lee I. Generalized Channel Inversion Methods for Multiuser MIMO Systems［J］. IEEE Transactions on Communica⁃tions，2009，57（11）：3489-3499.

童娟娟（1989-），女，硕士研究生，主要研究方向为无线通信系统中的预编码技术；

束锋（1973-），男，博士，研究员，博士生导师，发表期刊和会议论文100余篇，其中SCI/SCIE检索论文23篇，EI检索60多篇，论文被国内外学者引用265次，申请国家发明专利9项，已和正在主持国家层次项目三项。

Design of the Encoder and Decoder Based on the 1553B Bus Protocol*

YANG Yong1*，WANG Zhanling1，2，ZHANG Dengfu2
（1.PLA Unit 93594，Bayannaoer Inner Mongolia 014413，China；2.AFEU，Aviation and Aerospace Engineering College，Xi’an 710038，China）

Abstract：The encoder and decoder are the indispensable components of the 1553B bus protocol chip. In order to research the IP core of 1553B bus autonomously and meet the extensive demand for 1553B protocol chip. This arti⁃cle designs the encoder and decoder based on the 1553B bus protocol. Using the top-down and independent meth⁃ods and synchronization ways of designing the encoder and decoder，it improves the reliability and lessens the inter⁃ference between the data efficiently，and resolves the metastability issue. After simulation and verification，the re⁃sults indicate that the functions of encoder and decoder are all achieved. At last，the testing on the FPGA hardware platform achieves effective results，the results correspond with the design demand.

Key words：1553B bus；encoder and decoder；FPGA；Verilog HDL

doi：EEACC：6120B10.3969/j.issn.1005-9490.2016.01.010

收稿日期：2015-03-11修改日期：2015-03-31

中图分类号：TN919.3

文献标识码：A

文章编号：1005-9490（2016）01-0041-05