链式衬砌节段长度对隧道抗错断效果的影响研究

谷柏森++吴建勋++宋磊++刘金栋

摘要：针对活动断裂带引起的隧道结构安全问题，依托四川棋盘石公路隧道，基于链式衬砌的抗错断设计理念，分析在逆断层错动时不同链式衬砌节段长度下，隧道结构围岩压力、塑形应变及最大主应力的变化规律与分布特征，探讨合理的衬砌节段设计长度，可为同类工程抗错断设计提供参考。

关键词：断层错动；抗错断设计；链式衬砌；受力变形特征

中图分类号：U455.46

文献标志码：B

引言

活动断裂引起的错动破坏与地震破坏是当今制约隧道结构安全的两大问题。在铁路和公路的选线设计中，不可避免地会遇到隧道穿越（或接近）活动断裂带的情况。如何减小断层错动对隧道结构稳定性及安全性的影响是设计与施工的难点之一。

调研表明，由于隧道结构和断层错动之间的影响关系不明确，致使抗断设计中参数的选取十分困难。为完善隧道结构抗断层错动设计，评判处于活断层区域隧道结构的安全性，本项目依托棋盘石隧道，采用数值分析的手段研究活动断裂错动位移对隧道复合式衬砌结构的影响，探讨不同节段长度在断层错动位移下的力学响应，为合理设计隧道结构抗错动提供依据和参考。

1 链式衬砌计算模型

1.1 工程概况

工程为棋盘石公路隧道，隧址区发育F22及F22-l逆冲断层，其中，F22-l断层近似正交穿越洞身，倾角65°～80°，长120m.宽40m.两侧影响带约50m，该段隧道埋深120～180m，如图l所示。断层上下盘岩性均为灰岩，岩体结构遭到破坏，呈碎裂状，完整性较低，综合判定断层内围岩为V级，两侧围岩为Ⅳ级。

隧道横断面为两车道标准断面，初衬为C20素混凝土，二衬为C25钢筋混凝土，穿越断层时进行小导管全断面注浆，形成锚固区。考虑隧址区断层分布范围广，日后活动的可能性较大，为提高衬砌结构抗错断性能，采取“衬砌节段十剪切缝”的链式结构方案，如图2所示。

1.2 三维数值计算模型与力学参数

利用ABACUS有限元软件建立三维计算模型，考虑隧道主体结构、断层及其影响带范围，模型尺寸为160m×70m×（120～l80）m，断层与隧道轴线正交，倾角80°，如图3所示。

计算中涉及的围岩、初衬、二衬及剪切缝均定义为实体单元，其中初衬与剪切缝为线弹性材料，围岩、断层及二衬节段视为弹塑性材料。围岩、衬砌材料的力学参数依现场地勘及现行规范取值；锚固区重点考虑围岩粘聚力与弹性模量的增强作用，按提高20%后计算；剪切缝依工程经验，按强度折减法，折减为二衬材料的1%，关键参数见表l。

1.3 错动模拟

本文仅分析隧道投入运营后，断层错动引起的结构受力变形特征，不考虑施工扰动。断层单次错动0.5cm，累计错动最大为20cm（节段长度取lOm），沿坐标投影方向施加，考虑断层倾角的影响。

模拟分两步：隧道和围岩在地应力下达到平衡；逆断层错动（下盘不动，上盘抬升）。第一步时，模型底部竖直方向、四周水平方向施加固定约束，上部边界保持自由；第二步时，上盘地面、左侧面施加位移边界条件以模拟上盘抬升。

1.4 工况设计

共设计4组工况，其中工况l为对比模型，未采用链式衬砌结构；工况2到工况4的剪切缝宽度均为0.3m，考虑现行的二衬模筑工艺，取节段长度为5～10m，详见表2。

2 二衬结构力学响应分析

依据计算结果，分析断层错动位移条件下，二衬背后压力、塑性应变及最大主应力的变化规律与分布特征，以同等错动位移下的力学指标或允许最大错动位移为判据，评价链式衬砌的抗错断效果。

2.1 二衬背后压力变化规律与分布特征

四种工况下，二衬压力分布如图4所示。

工况l中，围岩压力分布比较均匀，沿断层区左右对称，拱腰处的围岩压力最大，仰拱处最小。相比于工况3和工况4，工况2的围岩压力在上盘的分布比较均匀，端部受边界条件的影响，压力增大。随着节段长度的逐渐增大，断层错动处受力集中，并逐渐向下盘区域转移；当节段长度为lOm时，下盘受上盘的影响在断层错动处也产生了压力集中现象。

取四种工况下围岩压力最大处的点绘制该处围岩压力随断层错动位移的变化关系，如图5所示。

二衬背后压力随着错动位移的增加呈线性增加，虽然在工况l和工况2中，关系曲线有一定的振荡，但整体趋势未变。节段长度为7m时，二衬背后压力的变化较缓慢，在错动位移刚开始时的20mm范围内，围岩压力的变化较小。当节段长度为lOm时，二衬破坏时所能承受的围岩压力最大。

取工况4节段长度为lOm，绘制错动位移分别为2cm、8cm、14cm、19cm时二衬围岩压力发展变化规律，如图6所示。

错动位移为2cm时，围岩压力在二衬上的分布比较均匀，断层上盘的围岩压力比下盘大，断层处的围岩压力较小；当错动位移为8cm时，断层处围岩压力逐渐增大；错动位移l4cm时，围岩压力逐渐向断层处集中；当错动位移为19cm时，围岩压力就集中在了断层处。依图6可以看出，围岩压力在二衬上的发展是一个从上盘逐渐向断层处集中的过程。

2.2 二衬塑形应变变化规律与分布特征

四种工况下隧道二衬等效塑性应变分布如图7所示。

工况l下塑性应变最大位置在二衬仰拱靠近断层处，贯穿整个节段。在靠近断层处的二衬顶部也出现了轻微的塑性应变集中现象；工况2下塑性应变最大值出现在二衬底部仰拱处，但没有贯穿整个节段，只是在剪切缝和隧道节段的接触部位有明显的塑性应变集中现象；工况3和工况4的塑性应变主要集中在错动面两侧二衬拱腰处，相应位置的上盘塑性应变现象明显。虽然在整个数值模拟过程中下盘并未发生位移，但是受断层错动的影响，下盘二衬相应位置也出现了塑性应变集中现象。endprint

相比工况3和工况4，工况2在较小的塑性应变情况下就发生了较大的位移，不能承受较大的位移错动。因此，较密的设置剪切缝，在一定程度上破坏了二衬结构的整体性，使得二衬结构不能较好的发挥自有优势，在很小的错动位移下就产生了屈服。

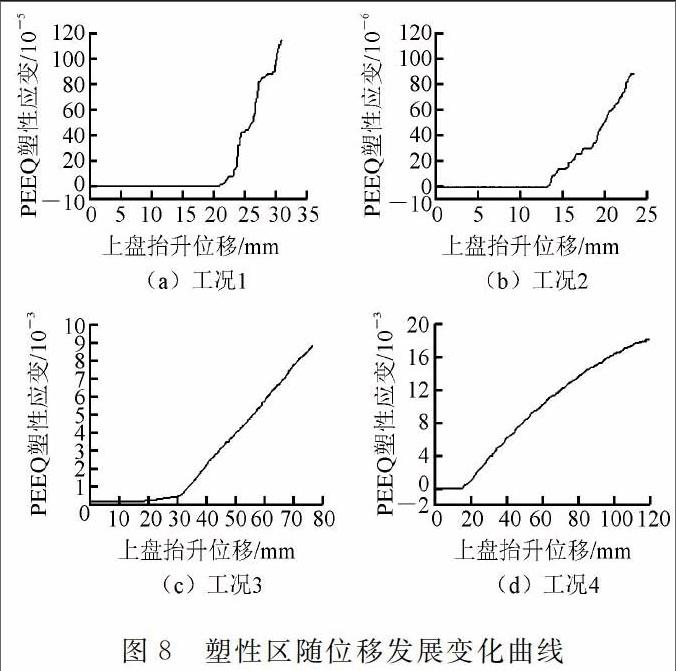
取各工况下塑性应变最大的点，绘制该点的塑性应变随断层错动位移变化的关系图，如图8所示。

在未设置剪切缝的工况l中，塑性应变在位移为20mm时开始产生，并随后迅速发展，直至破坏；在节段长度为Sm的工况2中，塑性应变产生的时间较早，大致在错动位移15mm时产生，破坏时的塑性应变也较工况l小；在工况3和工况4中，塑性应变也在错动位移达到20mm时产生，但是节段长度为lOm时的塑性应变较节段长度为7m时变化缓慢，破坏时的塑性应变较大。因此在3种节段长度中，从塑性应变的发展变化角度，把节段长度设置成lOm更有利于隧道结构抵抗断层的错动。

为了更好地研究塑性应变在二衬结构上的发展变化规律，取工况4节段长度为lOm时进行分析。截取断层错动位移分别为2cm、8cm、14cm、19cm时二衬塑性应变分布，如图9所示。

从图9可以看出，二衬塑性应变首先出现在上盘靠近断层带的节段，随着错动位移的增加，塑性应变逐渐向断层带内的节段发展，最后，塑性应变主要集中在断层滑动面附近的节段中。

2.3 二衬最大主应力变化规律与分布特征

四种工况下，二衬的最大主应力分布如图lO所示。不设置剪切缝时（工况1），在断层与围岩的接触处，二衬的顶部位置出现了应力集中现象，该处二衬的最大主应力最大，最小应力出现在拱脚位置；节段长度为5m时（工况2），最大主应力在二衬上的分布较均匀，最小应力仍然出现在拱脚和仰拱的位置；当节段长度为7m时（工况3），最大主应力出现在了仰拱位置，且受上盘影响，下盘断层处的二衬仰拱处最大主应力也较其他位置大；当节段长度为lOm（工况4）时，最大主应力集中现象出现在了断层内部的二衬顶部位置，应力分布情况与工况l的应力分布情况较类似。从图lO可以看出，断层内部二衬拱顶部位较其他位置危险，受力较大，结构容易破坏。

取四种工况下二衬的最大主应力集中点，绘制该处最大主应力与断层错动位移的变化关系，如图ll所示。

前3个工况中，断层错动位移为lOmm时，最大主应力基本未发生变化，随后，随着断层错动位移的增大而线性增大。相对于工况l，工况2在相同错动位移下的主应力偏小。在工况l和工况2中，该处应力随着位移的增大，从受拉逐渐变为受压。在工况4中，当断层错动位移为20mm时，主应力的变化不大，但随着位移的增加，主应力也逐渐加大。

取节段长度为lOm（工况4），绘制错动位移分别为2cm、8cm、14cm、19cm时二衬的最大主应力变化规律，如图12所示。

当错动位移为2cm时，只在断层下盘端部位置处出现了轻微的应力集中现象，断层处的受力较小。当位移逐渐加大时，断层位置处二衬拱脚和拱顶位置出现了较大的应力变化，且随着位移的增大，此应力集中的现象越明显。断层和围岩交界处的二衬顶部位置应力集中现象最为明显。

3 结语

（l）与普通无链式衬砌结构相比，尽管采取链式衬砌结构的工况2～工况4中出现了程度不一的应力集中现象，但隧道结构所能承受的断层错动位移、二衬背后压力、等效塑性应变及最大主应力均得到明显提升，验证了链式衬砌的抗错断效果。

（2）逆断层条件下，设置链式衬砌后，随节段长度增加，断层错动处应力集中现象逐渐凸显，应力集中区域逐渐由上盘断层边缘向下盘断层边缘发展。

（3）逆断层条件下，链式衬砌节段长度不宜过短。如工况2节段长5m，在较小的塑性应变情况下就发生了较大的位移，不能承受较大的位移错动；且较密的设置剪切缝，在一定程度上也破坏了二衬结构的整体性，使得二衬结构不能很好的发挥自有优势。

（4）计算表明，对于棋盘山公路隧道，采取链式衬砌结构，节段长度在7～lOm时，所能承受的围岩压力、塑形应变、最大主应力均大幅增加，结构受力性能更为优越，抗错断效果明显。同时考虑现行二衬模筑工艺，建议棋盘石隧道链式衬砌的合理节段长度取lOm。endprint