X—R控制图在沥青混合料生产质量控制中的应用

王同++李思李++田波

摘要：通过对沥青拌和站中沥青用量数据的统计分析，表明沥青用量在沥青混合料生产过程中存在波动性和规律性，运用统计学的方法对沥青用量进行分析，绘制了控制图，并对其进行修正，使其可以有效的对沥青拌和站的运行状态进行控制，保证沥青混合料生产环节的质量。

关键词：沥青混合料；质量控制；波动性；控制图

中图分类号：U414

文献标志码：B

引言

利用统计学原理对沥青混合料大量生产数据进行分析的结果表明，质量监测数据一般存在波动性和规律性两方面的性质。

正态分布是统计学中最重要、最基本的一种分布形式。对于质量控制，要求施工质量l00%满足性能要求，在大多数情况下是不可能实现的，只要控制指标值满足一定的保证率，就认为质量控制的结果是可以接受的。

在统计质量管理中，控制图作为一种重要的工具，是由美国休哈特博士于1924年创立的，他将数理统计方法引入，开始了统计质量控制的阶段。控制图由正太分布曲线演变而来，因此，运用控制图进行施工过程的质量控制能有效地控制工程质量的同时，也能科学地评价施工水平的高低。

1 数据波动性与正态性

1.1 波动性

根据对质量的影响程度，在数理统计上，把影响质量波动的因素分为偶然因素和系统性因素两大类。当过程仅受偶然因素影响时，过程处于统计控制状态（简称受控状态）；当过程中存在系统因素的影响时，过程处于统计失控状态（简称失控状态）。

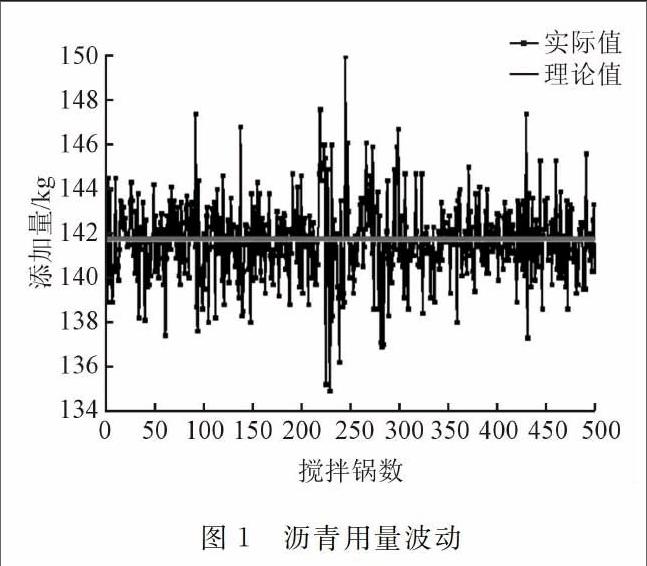
以拌和楼数据库中的沥青用量为例，图l为沥青实际用量与最佳用量的关系图，由该图可以看出，沥青的实际用量在最佳用量附近波动。

标准偏差σ可以反映样本的绝对波动状况，但当测量样本平均值不同时，只使用标准偏差不能完全反应出数据的波动性，因此用相对波动的大小，即变异系数更能反映样本数据的波动性。

变异系数是沥青路面动态控制中非常重要的特征量，表示数据相对波动的大小，也就是相对的分散程度，用Cv表示式中：σ为所测样本的标准偏差；X为所测样本的均值。

在施工质量管理中，应尽量减小沥青含量变异的大小，将沥青含量的波动性控制在一定范围内，减小其变异系数。

以每4盘沥青用量为l组进行统计，求得每组沥青用量的变异系数，结果见表l。由表l看出，样本组8、9、13的变异系数超过了3%，说明这2组数据的波动性较大，沥青用量的数据存在可疑，应检查设备是否出现问题。

1.2 正态性

上文提出，产品质量是存在波动的，但并不是说这种变动不可预测，无章可循。根据统计学理论，对数据进行数理统计分析，就可以找出质量波动的幅度，以及不同波动幅度出现的概率，这就是质量变异的统计规律。

正态分布通常只在区间（μ-3σ，μ+3σ）内研究正态总体的分布情况，只要质量检测值落在该范围内，则认为该结果是可以接受的；如果控制指标超过此范围时，应立即停工调整，直到恢复正常。

以拌和楼数据库中的沥青实际用量数据为例，将沥青实际用量进行统计，由图2可以看出，沥青实际用量呈现正态分布规律，因此可以使用正态分布的相关结论，对沥青路面施工进行质量控制。

2 休哈特控制图

从控制图的变化趋势中判断生产过程是否处于稳定状态的方法，将产品质量控制从事后检验改变为事前预防，这为保证产品质量、降低生产成本、提高生产效率开辟了广阔的前景，因此控制图在世界各国得到了广泛的应用。目前，均值控制图和极差控制图即X-R控制图通常用于沥青路面施工过程质量控制。

2.1 控制图原理

对于质量管理，正常情况下可以认为检测值服从于正态分布。如果忽略数据监测时的随机误差，在不产生系统偏差的情况下，随机抽样后测定的质量特征应满足下式

Xi～N（μ，σ） i=ι，2，…，n

（1）

因此根据正态分布的3σ原理，均值μ与标准差σ的取值多少，最终产品质量特性值Xi落在（μ3σ，μ+3σ）区间的概率为99.73%；而产品质量特征值的取值超出[μ-3σ，μ+3σ]范围的可能性为0.27%，大于μ+3σ或小于μ-3σ的概率为0

休哈特利用以上特性，取[μ-3σ，μ+3σ]范围作为控制界限构造了控制图，称为休哈特控制图，其中包括中心线（CL线）、控制上限（UCL线）、控制下限（LCL线）三条控制线。

2.2

X-R控制图

在X-R控制图中，中心线为控制指标的平均值；UCL线与LCL线分别为控制指标的上下控制界限，数据在该范围内波动属于正常状态。一旦被测数据落在该区域外，说明此时该项指标出现异常，为保证施工质量的稳定，应及时采取措施进行处理，避免系统出现大的问题。因此不难理解，若控制上下限范围越小，说明施工水平越高，数据变异性或波动性越小；反之亦然。

在X控制图中

同理，R控制图的控制界限为

式中：CL-X为R控制图中心线，某阶段指标检测结果平均值；UCL-X为R管理图中的质量控制上限；LCL-X为R管理图中的质量控制下限；x为每组平均值X的平均值；σR为极差R的方差；R为每组极差R的平均值；d2、d3、A2、D3、D1为系数，其大小可根据样本大小n计算3σ控制界限参数表得到。

应用控制图进行质量控制最主要目的是判断某一生产过程是否处于稳态或者可控状态。根据数理统计计算可知，判断过程处于稳态有以下三个准则。

（l）控制图中连续25个点子落在UCL线与LCL线之间。

（2）控制图中连续35个点子中，最多出现1个点子落在UCL线与LCL线之间之外。

（3）控制图中连续lOO个点子中最多出现2个点子落在UCL线与LCL线之间之外。endprint

三条准则对应不同数量的测试数据。

3 实例分析

上文介绍了控制图的基本原理以及休哈特控制图的计算过程，本节以沥青用量为例，探讨利用统计学中平均值 极差控制图对关键参数进行控制的方法。

通过沥青混合料数据采集系统，对一段时间内拌和楼的生产数据进行监控，针对沥青用量抽取了200个数据进行分析，每组样本大小为4，共分成了50组，每组数据的平均值X与极差R值，详见表2。

根据2.2节所提供的公式计算X控制图与R控制图的控制界限：对于X控制图，由式（2）、（ll）、（12）得CL=141.741.UCL=144.768，LCL=138.714。

对于R控制图：由式（5）、（13）、（14）得CL=4.152，UCL=9.475，LCL=O。

系数可按计算3σ控制界限参数表取值，其中：A2=0.7289，D3=0，D4=2.282。

将样本数理统计量X和R逐一描点在图上，用折线连接，得到XR控制图，如图3、4所示。

由图3、4中样本点状态可以看出以下几点。

（l）X控制图中第7号样本点超出上控制线。

（2）极差R控制图中第8、9、l3、38号样本点超出上控制线。

（3）X控制图中处于控制界限内的样本点基本平均分布在中心线附近。

（4）极差R控制图中处于控制界限内的样本点多数在中心线下方。

经过确定，7、8、9、38号样本超出上控制线为系统稳定性原因所引起的，删除这些样本之后重新确定控制界限。

首先按以下公式计算

式中：Xd为剔除样本后的平均值；md为剔除的样本组数；Rd为剔除一组的极差；m为原有的样本组数。

计算得

对于X控制图修正后的控制界限，由式（2）、（ll）、（12）得：CL=141.67， UCL=144.402， LCL=138.936。

对于R控制图，由式（5）、（13）、（14）得：CL=3.75，UCL=8.555， LCL=O。

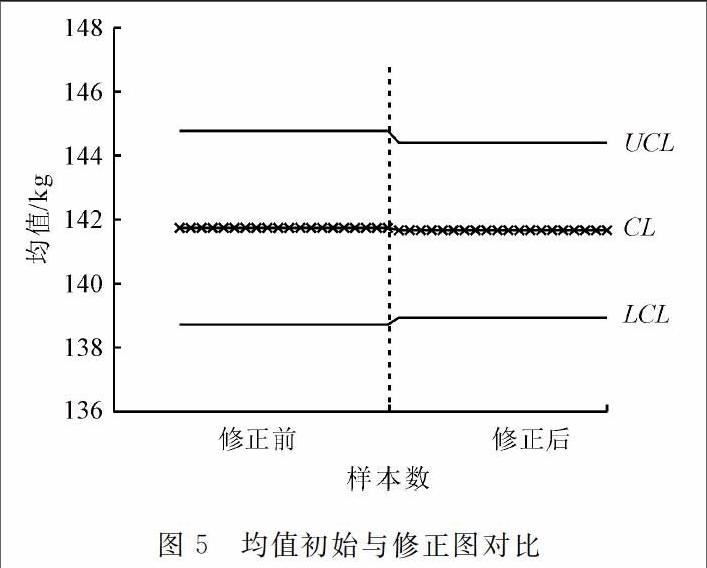
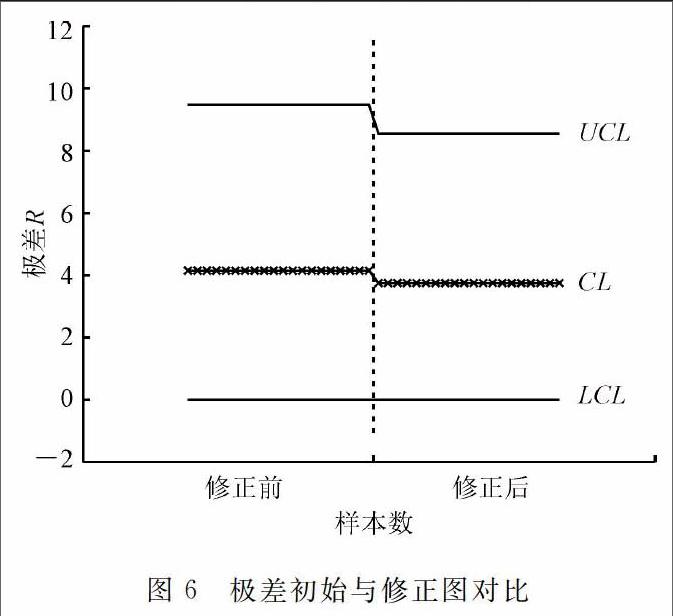
图5、6为修正前后控制图变化情况，由该图可以看出修正后控制图的中心线下移，控制界限变窄，说明控制水平得到提高。

经过修正的控制图在使用过程中都要经过不断改进，以保证每个阶段均处于可控状态，要提高控制的质量水平，其关键是预防和纠正措施。当认为控制的目的基本达到后，可不必继续修正控制图，而是进行定期抽样检测以检测是否保持现有状态即可。

4 结语

本文以拌和楼的沥青用量数据进行了数据波动性分析并运用控制图的方法进行了统计分析，可以有效的对拌和楼的运行状态进行控制。因此在沥青混合料生产过程中建立基于概率统计的质量控制体系，可以客观全面地检测评价路面施工质量，为施工质量控制提供基础数据，并为工程验收和实施按质支付提供依据。endprint