基于全局敏感性分析和贝叶斯方法的WOFOST作物模型参数优化

何　亮，侯英雨，赵　刚，邬定荣，于　强（. 国家气象中心，北京 0008；　. 德国波恩大学作物科学研究组，波恩 D-55；. 中国气象科学研究院，北京 0008；　4. 中国科学院地理科学与资源研究所陆地水循环与地表过程重点实验室，北京 000； 5. 澳大利亚悉尼科技大学生命科学学院，悉尼 007）



基于全局敏感性分析和贝叶斯方法的WOFOST作物模型参数优化

何亮1，侯英雨1，赵刚2，邬定荣3，于强4，5
（1. 国家气象中心，北京 100081；2. 德国波恩大学作物科学研究组，波恩 D-53115；3. 中国气象科学研究院，北京 100081；4. 中国科学院地理科学与资源研究所陆地水循环与地表过程重点实验室，北京 100101； 5. 澳大利亚悉尼科技大学生命科学学院，悉尼 2007）

摘要：作物模型参数的敏感性分析、标定和验证可以提高模型的效率和精准度，进而为模型应用做好准备工作。该研究结合参数全局敏感性分析方法以及贝叶斯后验估计理论的马尔科夫蒙特卡洛（Markov Chain Monte Carlo，MCMC）方法，以华北栾城站三年的冬小麦观测数据（叶面积和地上生物量）为参照，对WOFOST模型的55个品种参数进行了敏感性分析、筛选和优化。发现：1）对叶面积影响较大的参数为：生育期为0、0.5、0.6和0.75时的比叶面积、生育期为1.5时的最大光合速率、叶面积指数最大增长率；对地上干物质影响较大的参数为：生育期为1.5时的最大光合速率、生育期为0时的比叶面积、35℃时叶面积的生命周期、生育期为0时的散射消光系数、生育期为1.8时的最大光合速率、储存器官的同化物转换效率。2）潜在和雨养产量水平下，最大叶面积和地上生物量对参数的敏感性差异不大。3）马尔科夫蒙特卡洛方法（MCMC）可以对WOFOST模型品种参数较好地优化；设计的3种校正-验证方案中，第1种方案（用1998－1999年作为校正年份，1999－2000年，2000－2001年作为验证年份）模拟效果最好。4）优化后的参数，模型对潜在产量水平模拟较好，一致性指数均大于0.9，相对均方根误差小于20%；而对有水分胁迫的雨养情况下比潜在产量水平的模拟结果差，表明模型对水分胁迫的模拟不足。该研究为WOFOST模型区域应用和模型调整优化提供科学理论依据。关键词：模型；作物；优化；WOFOST；全局敏感性分析；MCMC；模型参数优化

何亮，侯英雨，赵刚，邬定荣，于强. 基于全局敏感性分析和贝叶斯方法的WOFOST作物模型参数优化[J]. 农业工程学报，2016，32（2）：169－179.doi：10.11975/j.issn.1002-6819.2016.02.025http://www.tcsae.org

He Liang， Hou Yingyu， Zhao Gang， Wu Dingrong， Yu Qiang. Parameters optimization of WOFOST model by integration of global sensitivity analysis and Bayesian calibration method[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2016， 32（2）: 169－179. （in Chinese with English abstract）doi：10.11975/j.issn.1002-6819.2016.02.025 http://www.tcsae.org

Email：heliang_hello@163.com

0　引　言

模型的标定（calibration）和验证（validation）等准备工作是基于机理作物模型应用的前提。对于基于机理的作物模型，参数众多。作物模型的很多参数（如比叶面积）不能通过田间观测直接获得，而是需要通过可观测的变量（如叶面积指数）进行反演。通过准确的方法获得模型参数是进行模型应用、提高模型可预报性的前提[1]。

根据观测值反推参数属于参数估计问题。对于线性方程或者简单的非线性方程可以用最小二乘法来解决。基于过程的作物模型，刻画了光合、干物质分配、土壤水分运移和蒸发等众多生物物理过程，往往包含的方程较多，模型的非线性效应很明显。对于一般的最小二乘法和非线性参数估计方法难以获得全局的最优解。一种常用的模型参数标定是基于蒙特卡洛试错法。这种方法根据以往的经验或者参数文献参考值重复和随机地选择参数，使得观测值和模拟值拟合程度指标：如决定系数（R2）、相关系数、均根方差等指标达到预期的要求，便认为此组参数为最优参数。这种方法带有很大的主观性并且工作繁杂，而且很难获得最可靠、最优的参数[2]。并且，这种参数估计方法计算量巨大，计算量随着参数数量呈几何级数增加。

为了避免上述缺点，基于过程的模型开始采用非线性参数优化方法，例如遗传算法[3]，普适似然不确定估计法（general likelihood uncertainty estimation，GLUE）[4]等，也有类似的参数估计软件出现，例如PEST（parameter estimation software）[1]。He等[5-6]利用GLUE方法对CERES-Maize的品种和土壤参数进行了估计，取得了很好的效果；房全孝[1]利用PEST对根系水质模型（root zone water quality model，RZWQM）的土壤和根系生长参数和作物遗传参数进行了优化，相比传统试错法的校正结果，有明显的参数优化效率。马尔科夫蒙特卡洛方法（Markov Chain Monte Carlo，MCMC）是基于贝叶斯统计理论的一种参数估计方法，其在模型参数估计已有应用。近年来，运用该方法来对基于过程的生物模型也有若干运用[7-10]。Makowski等[11]对比了GLUE和MCMC方法的参数优化效率，发现对一个非线性农业模型的22个参数估计时MCMC方法估计的误差比GLUE方法要小。对于这些非线性优化方法的应用过程当中，一个重要的问题是优化参数的选择和计算量。对非敏感参数进行优化不会提高模型的精度反而会成倍加大计算量。模型参数敏感性分析可以有效地区分和界定参数的敏感性和重要性，为优化参数选择提供有效筛选依据。参数的敏感性分析可以分为局部敏感性分析和全局敏感性分析。近年来，在过程模型的参数敏感性分析中，全局敏感性分析方法受到了学者们的亲睐[12-17]。这主要是因为全局敏感性分析方法不仅仅反应了单个参数对模拟结果的影响，而且可以定量参数与参数之间的相互作用对结果的影响。鉴于此，在对参数进行优化之前，先进行参数的敏感性分析，筛选出对模拟结果影响大的参数，然后再来优化。这可以使优化算法做到有的放矢、提高效率并且减少计算时间。

本研究选择全球得到广泛应用的WOFOST作物模型为研究对象。以冬小麦为实例，首先用全局敏感性分析方法对模型的参数进行参数筛选。然后采用马尔科夫蒙特卡洛（MCMC）的参数优化方法，对敏感的作物品种参数进行优化。以期探索一种普适的作物模型参数优化方法，为作物模型参数校正和模型应用提供一定的指导。

1　材料与方法

1.1试验站点和数据

本文所用到的试验观测数据在栾城站进行。栾城站位于河北省石家庄市栾城县（114°40′E，37°50′N，海拔50.1 m），为太行山前平原农业高产区的典型代表。本地主要气候类型是暖温带半湿润季风气候，多年平均太阳辐射为5 433 MJ/m2，平均气温为12.3℃，大于0℃积温为4 710℃·d，大于10℃积温为4 232℃·d，无霜期为200 d。丰富的光热资源满足一年二熟或两年三熟的作物生长。年降雨量大致为480 mm，降水分配不均，超过65%的降水集中在夏季。冬小麦生长季降水量仅仅120 mm左右，而整个生长季的需水量达460 mm以上，降水量难以满足冬小麦生长需要[18-21]。

在栾城站进行了冬小麦的水分池试验，试验的时间是1998年10月到2001年6月，一共设计了16个水分试验池，每个试验池的面积为50 m2（5 m×10 m），四周由厚24.5 cm和深1.5 m的水泥墙隔离，防止不同水分处理的水分侧向运动。一共3个冬小麦的生长年度，冬小麦的品种为高优503，小麦播种量为135 kg/hm2，采用人工播种，播种前深翻土壤到15 cm，播种时施肥磷酸二氨480 kg/hm2，复合肥1 600 kg/hm2。冬小麦生育期共设计5种不同水分处理，每个水分处理重复3次，处理包括：充分灌溉，雨养，返青期水分胁迫，拔节期水分胁迫，灌浆期水分胁迫。模型标定一般选择充分灌溉和雨养的两种情况，结合WOFOST模型的潜在生长和水分限制生长的两种产量水平，本研究选择了充分灌溉和雨养两种情况的数据。太阳辐射、最高最低温度、降水、气压、湿度等气象因子由试验站的自动气象观测站测定。干物质和叶面积每隔5～7 d测定一次。土壤水分测定由中子仪在田间每5 d测定一次，测定深度为20～160 cm，间隔20 cm。1998年到2001年3个冬小麦生育期的气候基本特征如表1。栾城站的WOFOST土壤参数如表2。其他有关本次试验的更详细的描述可见Zhang等[19]和Chen等文献[20-22]。

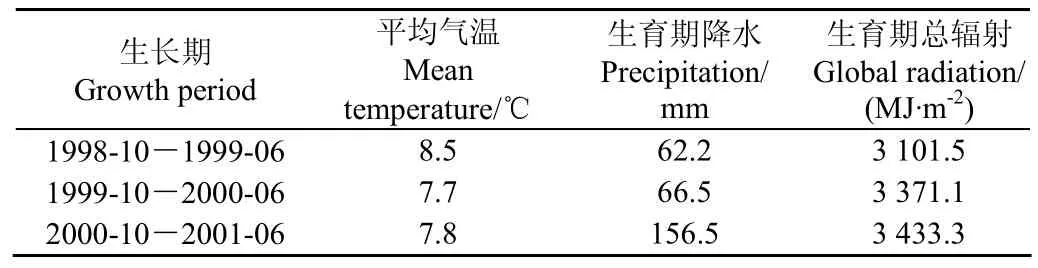
表1　1998－2001年3个冬小麦生育期的基本气候特征Table 1　Climate characteristics in three winter wheat seasons between 1998 and 2001

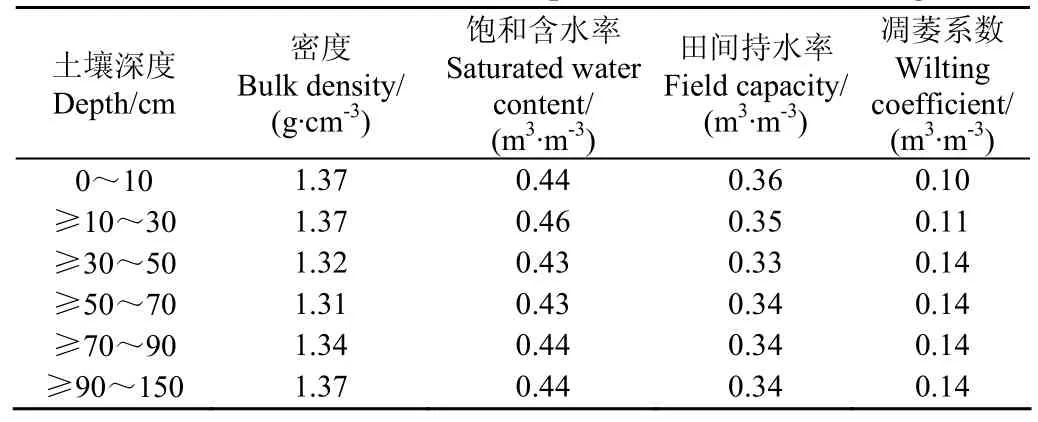
表2　栾城站的土壤属性特征Table 2　Soil characteristic parameters in Luancheng

1.2WOFOST模型

WOFOST模型是由荷兰瓦赫宁根大学开发的一个根据气象、土壤条件和管理措施模拟作物根、茎、穗生物量和土壤水分动态的模型。几十年来，它已经在学术和工业界得到了广泛应用。以下对模型机理进行简略介绍，更加详细的模型说明可以参考官方网站：www.supit.net。它模拟的主要过程包括作物发育、二氧化碳同化、呼吸作用、作物蒸腾、干物质分配、叶面积增长、干物质和叶片衰老、死亡、土壤水分平衡等过程[23-24]。WOFOST模型是一个抽象化通用的作物模型，也就是对各种作物的生长发育过程描述是一致的。它通过改变作物干物质分配和植物结构有关遗传参数来实现对不同作物的区分和模拟。它可以模拟3种产量水平即：光温限制的潜在产量、光温水限制的雨养产量以及光温水肥限制可获得产量。它通过逐日气象数据进行驱动，通过土壤、管理和作物参数数据限制和调整作物的生长过程。气象数据包括太阳辐射、最高、最低气温、早晨的水汽压、2米高度的平均风速、降雨量。土壤数据主要为田间持水率、饱和含水率、凋萎系数和导水率，如果需要模拟地下水的影响，则还需提供土壤水分特征曲线和导水率曲线参数。最重要的就是作物参数，其中包括不同发育阶段所需要的积温、光周期影响因子、不同生育期的最大光合速率、不同生育期的比叶面积、干物质分配系数、干物质和叶片的死亡率等。其中，不确定性最大的参数也就是作物品种参数。对于作物品种参数的详细描述可见表3。

表3　WOFOST品种参数上下限和分布Table 3　Upper and down bound of cultivar parameters in WOFOST

1.3全局敏感性分析方法

1.3.1扩展傅里叶幅度检验法

全局敏感性分析方法很多，包括：Morris参数筛选法、基于方差的Sobol法、傅里叶幅度检验法（Fourier amplitude sensitivity test，FAST）、扩展傅里叶幅度检验法（extended Fourier amplitude sensitivity test，EFAST）等[25]。本研究采用样本数要求低，计算高效的EFAST法，它是Saltelli等[25]结合了Sobol法和傅里叶幅度法两种方法的优点提出了一种新的全局敏感性分析方法。其算法的基本思想是分解参数对模型结果的方差，把参数敏感性分为两种类型：单个参数对结果的影响和参数之间耦合对模型结果的影响。其中单个参数独立作用是用主敏感性度指数（main effect）衡量，而参数相互作用则用总敏感度（total effect）和主敏感度的差别衡量。算法简单介绍如下：

模型y＝f（x1，x2，…，xk）可用合适的转换函数转换为y＝f（s），对f（s）进行傅里叶变换，

式中Ns为取样数，。

模型的总方差分解为

式中Vi为参数xi输入变化单独引起的模型方差，Vij为参数xi通过参数xj作用贡献的耦合方差，Vijm为参数xi通过参数xj，xm作用贡献的方差，则依次类推，V1，2，…，k为参数xi通过x1，2，…，k贡献的方差。通过归一化处理参数xi的一阶敏感性指数Si定义为

参数xi的总敏感性为

式中V-i为不包括参数xi的所有参数方差之和。算法详细的介绍参考Saltelli等文献[25]。

1.3.2敏感性参数选择和模拟设计

主要的参数说明和参数范围见表3。其中品种参数的范围选择来源于模型文档提供的合理的范围。以上所有的变量都服从均一分布，见表3。其中关于WOFOST模型中控制生育期的参数：出苗到开花的积温（TSUM1）和开花到成熟的积温（TSUM2）是根据观测实际算出。模型的其他参数：气象数据、播种日期、土壤参数都为实际的观测。模型考虑两个输出，最大的叶面积指数（MAXLAI）和地上生物量（TAGP）。考虑两种产量水平即潜在和水分限制。在EFAST方法中每次的敏感性计算需要运行n×p次，其中n为采样数量，p为参数个数。在EFAST方法中认为参数采样个数大于65倍的参数个数为有效（即采样个数≥参数个数×65），因此，为减少模拟次数，先计算敏感性结果随n的收敛性，大致在n 取80左右结果收敛，本研究采样大小n取150，采用EFAST方法，一共需要模拟3（3年）×150×55（参数）＝24 750次。敏感性计算框架结合R语言（http://www.r-project.org/）的Sensitivity包。用R语言编写程序调用WOFOST的函数，用Sensitivity包生成参数样本，然后交给WOFOST计算，最后利用Sensitivity包分析和计算模拟结果的敏感性。更为详细说明见何亮等的文献[13]。

1.4贝叶斯方法

1.4.1马尔科夫蒙特卡洛

对于作物模型的驱动数据、模型参数和模型输出，公式描述为

式中yi代表模型n个输出，例如生物量，叶面积等。xi为模型驱动因子，如温度，太阳辐射和降水等。θ为模型参数，例如作物品种参数，土壤参数等，εi为模型的随机误差，均值为0，方差为σ2，未知。

参数估计的问题就是已知xi和yi，来估计模型的参数θ。统计学中核心概念似然函数（Likelihood function），它是观测量的联合概率分布，满足

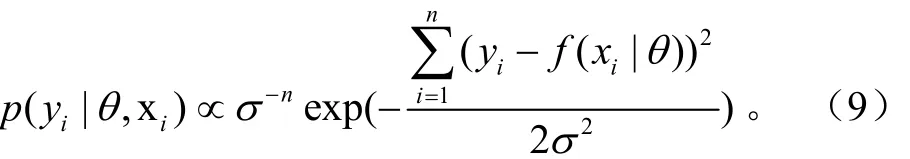
根据贝叶斯统计观点，参数也满足一定的概率分布，假设参数的先验分布为p（θ）。根据贝叶斯公式，得到参数的后验分布为

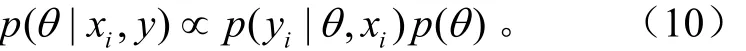
要得到后验概率密度，关键是要解出高维的联合概率分布函数p（yi|θ, xi），贝叶斯统计方法求这个高维的概率密度函数的思路是求出每一个参数的边缘分布，如

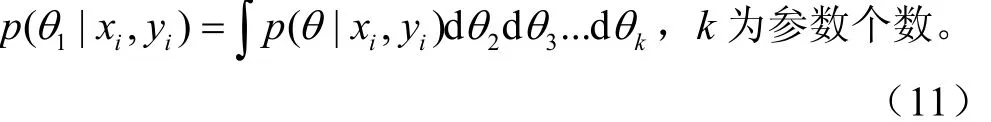
计算该边缘分布有两个难点：第一是归一化常数未知，第二是高维数值积分的困难。鉴于此，为解决此问题，出现了一系列的马尔科夫链蒙特卡罗（MCMC）算法。

马尔科夫蒙特卡洛（MCMC）基本思想是产生一个马尔科夫链，以目标分布为平稳分布，根据马尔科夫理论，一个马尔科夫链从任意初值出发，都会收敛到平稳分布。

马尔科夫的基本原理是：时间序列上，某一时刻t的状态，只与前一个时刻t-1有关，与其他时刻无关，这样的随机时间序列θ为马尔科夫链。

设{θt}t＞0为空间Θ上的齐次马尔科夫链，即：转移概率函数p（.，.）与时间t无关，转移概率函数为

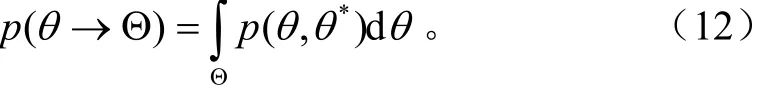
p（θ,θ*）为马尔科夫链的转移核，即为推荐分布。对于分布π（θ），满足

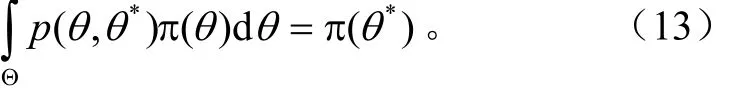
如果∀θ*∈Θ，则π（θ）为转移核p（θ,θ*）的平稳分布。当某θt～π（ θ），则θj～π（θ）， j＝t＋1，…理论上讲，无论θ0取何种分布，经过长时间搜索后，θt的边缘分布即为平稳分布π（θ），则称马尔科夫收敛[26]。

1.4.2MCMC采样方法

常用的MCMC采样方法有Metropolis 算法、M-H （metropolis-hastings）算法、Gibbs采样和自适应的Metropolis算法[27]。本研究用M-H抽样方法，步骤为：1）构造合适的建议分布q（⋅| θt）；2）根据先验分布g产生θ0；3）从（|t）q⋅ θ中产生候选点θ；4）从均匀分布U（0，1）中产生参数矩阵U；5）判断：若，则接受θ′，并令θt＋1＝ θ'，否则令θt＋1＝ θt；6）增加t，返回到第3步。

1.4.3MCMC优化参数选择、模型优化和验证方案

本研究中，共涉及3个年度的试验数据，如表1。用来优化的观测数据为生育期内不同时间段观测的地上生物量和叶面积指数，每年包括雨养和充分灌溉2套地上生物量和叶面积观测数据。参数估算方法中似然函数（式9）的构建是同时考虑了叶面积和生物量。待优化的作物品种参数为参数敏感性分析后，选取的较敏感的参数。由于3个季节是同一个品种，模型优化和验证设计3个情景，如表4：分别用其中一年的所有全灌溉和雨养的数据作为模型的校正优化，其他剩下两年作为模型的验证。模型待优化的参数选择依赖于全局敏感性分析的结果，这将在2.2.1节中详细介绍。模型校正和验证的过程用观测和模拟的一致性指数（index of agreement，d，见式14）和相对均方根误差（relative root mean square error，RRMSE，见式16）来评价，d越接近1，RRMSE越小，说明模拟精度越高。

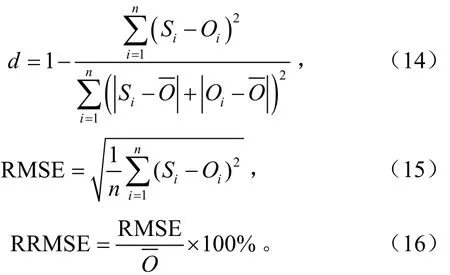
式中d为一致性指数，RMSE（root mean square error）为均方根误差，RRMSE为相对均方根误差，Si为第i个模拟值，Oi为第i个观测值，O为观测值的均值，n为样本数。

表4　WOFOST模型的不同校正-验证方案Table 4　Different plans for calibration and verification of WOFOST model

2　结果与分析

2.1全局敏感性结果

2.1.1潜在产量水平下的参数敏感性

在潜在产量水平下，如图1a，对于最大叶面积指数（MAXLAI），一阶敏感性指数最大的前5个因子依次为：生育期为0时的比叶面积（SLATB00）、生育期为0.5时的比叶面积（SLATB050）、生育期为0.6时的比叶面积（SLATB060）、生育期为0.75时的比叶面积（SLATB075）、生育期为1.5时的最大光合速率（AMAXTB150），其敏感性值分别为12.8%、2.7%、2.7%、2.5%、2.5%，其他参数的值分别小于1%；全局敏感性指数最大的前5个参数与一阶敏感性指数一样，其值分别为17.4%、4.4%、3.6%、3.4%、3.3%，但是对于参数SPAN（35℃时叶面积的生长周期）也较大，排在第六，值为1.9%，其余的参数分别小于1%。

如图1b，对于地上生物量（TAGP），一阶敏感性指数最大的前5个因子依次为：生育期为0时的比叶面积（SLATB00）、35℃时叶面积的生命周期（SPAN）、生育期为1.5时的最大光合速率（AMAXTB150）、储存器官的同化物转换效率（CVO）、生育期为1.8时的最大光合速率（AMAXTB180），其值分别为6.1%、4.1%、2.6%、2.2%、1.8%，其他参数的值分别小于1%；全局敏感性指数最大的前5个参数与一阶敏感性指数一样，其值分别为8.2%、5.3%、3.1%、2.9%、2.3%，其余的参数分别小于2%。

2.1.2雨养产量水平下的参数敏感性

在雨养产量水平下，如图2a，对于最大叶面积指数（MAXLAI），一阶敏感性指数最大的前5个因子依次为：生育期为0时的比叶面积（SLATB00）、生育期为0.5时的比叶面积（SLATB050）、生育期为0.6时的比叶面积（SLATB060）、生育期为1. 5时的最大光合速率（AMAXTB150）、生育期为0.75时的比叶面积（SLATB075）、其值分别为12.1%、4.8%、2.1%、2.1%、1.2%，其他参数的值分别小于1%；全局敏感性指数最大的前4个参数与一阶敏感性指数一样，其值分别为15.6%、6.3%、3.5%、2.8%，参数RGRLAI（叶面积指数最大增长率）也较大，排在第5，值为2.7%，其余的参数分别小于2%。

如图2b，对于地上生物量（TAGP），一阶敏感性指数最大的前5个因子依次为：生育期为1.5时的最大光合速率（AMAXTB150）、生育期为0时的比叶面积（SLATB00）、35℃时叶面积的生命周期（SPAN）、生育期为0时的散射消光系数（KDIFFTB00）、生育期为1. 8时的最大光合速率（AMAXTB180），其值分别为4.8%、4.4%、2.6%、2.0%、1.3%，其他参数的值分别小于1%；全局敏感性指数最大的前5个参数分别是生育期为0时的比叶面积（SLATB00）、生育期为0.5时的比叶面积（SLATB050）、35℃时叶面积的生命周期（SPAN）、生育期为1.8时的最大光合速率（AMAXTB180）、叶龄的低温阈值（TBASE），其值分别为23.0%、7.1%、6.7%、6.6%、4.2%，其余的参数分别小于4%。

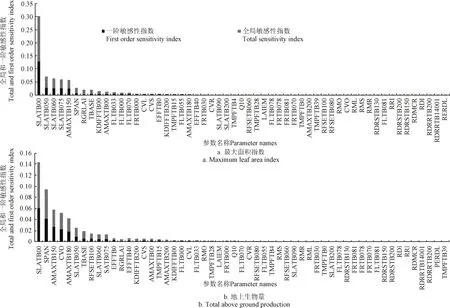
图1　潜在产量水平下的扩展傅里叶幅度检验法的敏感性分析结果Fig.1　Sensitivity results of extended Fourier amplitude sensitivity test in potential yield level

2.2马尔科夫蒙特卡洛（MCMC）优化

2.2.1马尔科夫优化参数选择、初值和先验分布

根据上节的敏感性结果，选择叶面积和干物质敏感较大的参数作为优化对象。其中主要包括以下11个参数：生育期为0时的比叶面积（SLATB00）、生育期为0.5时的比叶面积（SLATB050）、生育期为0.6时的比叶面积（SLATB060）、生育期为0.75时的比叶面积（SLATB075）、生育期为1.5时的最大光合速率（AMAXTB150）、生育期为1.8时的最大光合速率（AMAXTB180）、RGRLAI（叶面积指数最大增长率）、35℃时叶面积的生命周期（SPAN）、生育期为0时的散射消光系数（KDIFFTB00）、叶龄的低温阈值（TBASE）储存器官的同化物转换效率（CVO）；这11个参数的初值是根据观测值，先用试错法手动大致调整参数，使观测叶面积和干物质趋势大致一样时的参数值。这11个参数的初值如表5，每个参数的先验分布都为均一分布。在优化的过程中，对于11个参数给予±10%的上下扰动。其他敏感性不大的参数采样模型中默认的参数。对于控制生育期的参数：出苗到开花的积温（TSUM1）和开花到成熟的积温（TSUM2）是根据观测实际算出。

2.2.2不同校正优化方案得到的参数比较

模型优化采样3000次，收敛的判断是做出迹图（trace plot），即将所产生的样本对迭代次数作图，生成马氏链的一条样本路径。如果当采样次数足够大时，路径表现出稳定性没有明显的周期和趋势，就可以认为是收敛（由于篇幅，省略了迹图）。MCMC优化后，待参数趋于收敛后，11个参数得后验分布情况（由于篇幅，省略了11个参数的后验概率分布图）。根际参数的后验分布，把后验分布的均值作为参数的优化值。3种优化方案得到的参数如表6。总体来看，三种优化方案的各个参数变异系数相差较小，最大的叶龄的低温阈值（TBASE），为3%。不同的优化方案下，优化后的参数变异性小，说明马尔科夫蒙特卡洛（MCMC）方法在不同环境下的优化可靠性较好。

图2　雨养产量水平下的扩展傅里叶幅度检验法的敏感性分析结果Fig.2　Sensitivity results of extended Fourier amplitude sensitivity test in rain-fed yield level

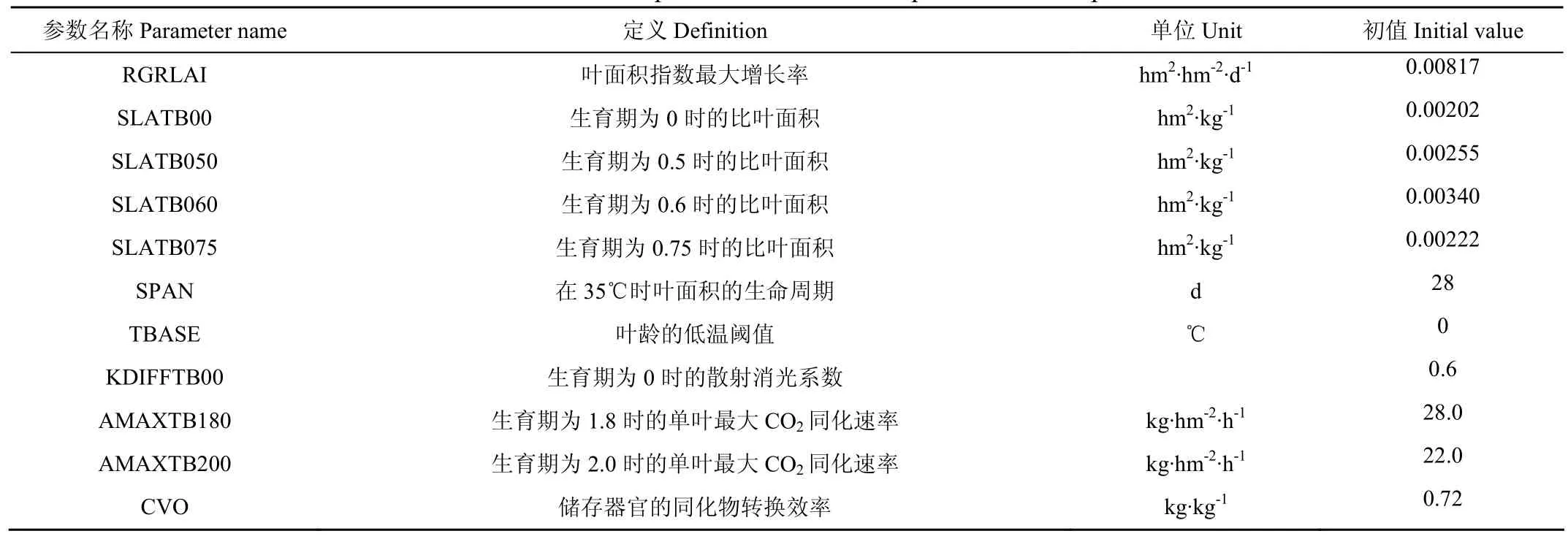
表5　WOFOST中11个待优化的品种参数初值和先验分布Table 5　Initial value and prior distribution of 11 parameters for optimization

表6　不同参数优化策略下的WOFOST作物品种参数取值Table 6　Estimation results of crop parameters of winter wheat for WOFOST in different parameter estimation plans

2.2.3不同优化方案的模型校正和验证结果

本研究设计了3种模型校正-验证方案。对观测的叶面积指数、地上干物质进行了验证。通过对比分析不同的校正-验证方案，选择较优的方案。图3和表7是方案1的详细校正和验证结果。其他2种方案，处于简洁需要，给出总体的验证结果，如表8。

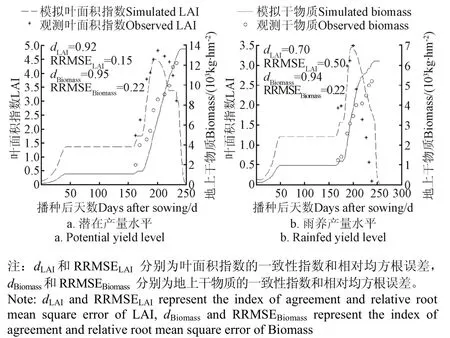
图3　方案1（1998-1999季节数据作为校正）模型优化结果Fig.3　Model calibration of plan one （data of 1998-1999 as calibration）

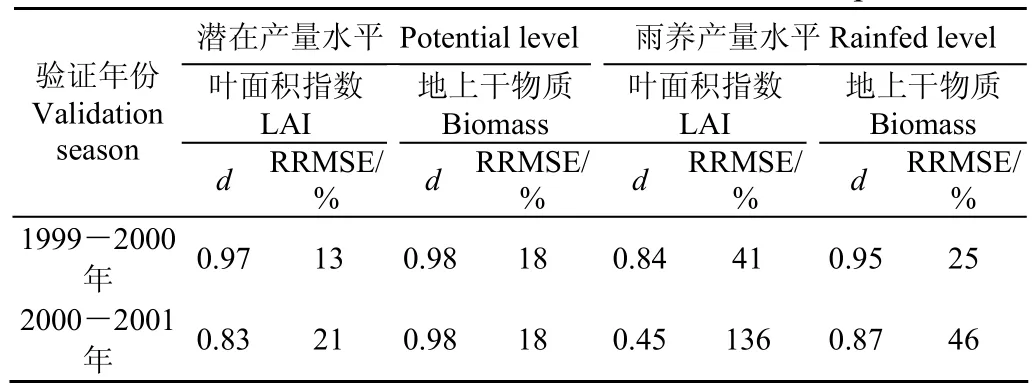
表7　方案1的优化参数在其他2季的模型验证Table 7　Model verification in other two seasons in plan one

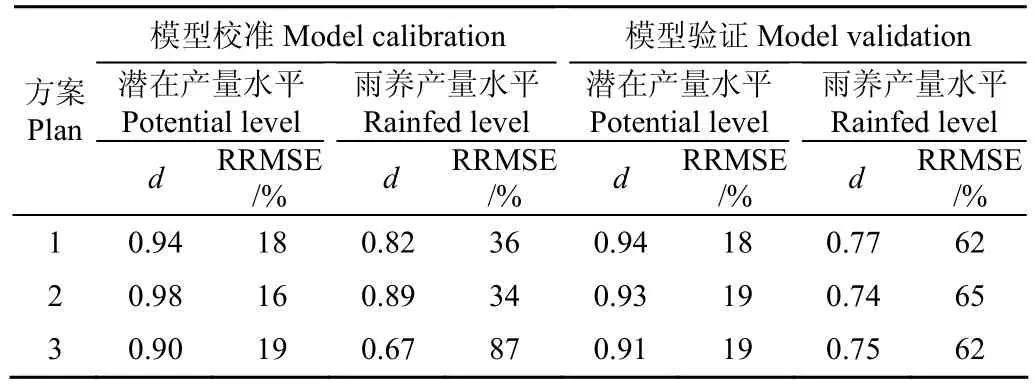
表8　3个优化方案叶面积指数和干物质模拟校正和验证结果精度比较Table 8　Comparison of LAI and biomass simulation accuracies of different plans of model calibration and verification

从方案1的校正结果看（图3），模型对潜在的叶面积和干物质模拟的很好，一致性指数d分别为0.92，0.95，相应的RRMSE分别为15%，22%；对于雨养情况下，叶面积指数模拟较潜在情况下要差，一致性指数小于0.8，但模型对雨养情况下的干物质模拟也较好，一致性指数达到了0.94，RRMSE为22%；从方案1的模型验证来看，如表7：潜在产量水平下，模型对2a的叶面积和干物质都模拟较好，一致性指数d都大于0.80，RRMSE小于21%。雨养产量水平下，模型在2000-2001年的叶面积指数模拟稍差，一致性指数仅仅为0.45，RRMSE达到了136%；

比较3个校正-验证方案，如表8，从模型验证的角度看，在潜在产量水平下三种方案都很好，一致性指数都不小于0.90，且RRMSE都小于20%。从雨养产量水平下一致性指数在0.74到0.77之间，雨养下的RRMSE都较大。综合潜在和雨养两种情况而言，方案1较其他两个方案略好。

3　讨　论

3.1参数的全局敏感性

本研究首先用扩展傅里叶幅度检验法（EFAST），分析了潜在和雨养两种生产水平下，55个WOFOST品种参数的敏感性的大小。从结果看，最大叶面积（MAXLAI）、地上生物量（TAGP）对于光合速率相关的参数，如生育期为1.5时的最大光合速率（AMAXTB150）、生育期为1.8时的最大光合速率（AMAXTB180），以及有关比叶面积的参数，如，生育期为0时的比叶面积，SLATB00等反应较为敏感。这是因为不同生育阶段的最大光合速率是限制光合作用大小的主要原因，是控制物质源的根本参数。而对于叶面积，比叶面积参数、最大叶面积增长率是控制叶片生长的关键参数，比叶面积控制了单位物质转换成叶面积的大小，因而叶面积对这些参数敏感性较强。从其他主流的作物模型参数敏感性分析来看，例如APSIM模型中的谷粒最大灌浆速率和辐射利用效率[13]，CERES模型中的光能利用率[16]都是制约同化物质量大小的基本参数。与Wang 等[12]对WOFOST玉米的参数分析比较来看，本研究有些差别，Wang等的研究中叶片在35℃生命周期（SPAN）为对干物质积累最敏感的参数，差别的原因可能是作物类型的不一致，因为作物类型的不一样，不同参数的取值范围就有差异。与Ceglar等[28]对WOFOST玉米的分析比较，比叶面积都是比较敏感的参数。

从不同产量水平下的参数敏感性结果看，最敏感的参数基本上是一致的，如图1和2。这也说明不同的产量水平下，模型的最大叶面积、地上生物量对模型参数的敏感性具有一致的表现，WOFOST模型的结果和作者对APSIM模型[13，29]分析结果基本是一致的。因而可以断定，产量水平不是造成模型输出对品种参数敏感性差异的原因。

Wang等[12]证实模型参数范围、采样次数对敏感性的结果影响很大。对于参数取值范围而言，不同的作物类型有不同的取值。本研究的参数范围是在前人的基础上结合模型说明里面的取值给定，没有考虑参数范围变化对敏感性结果的影响，这主要是基于本研究中参数敏感性的主要目的是为了客观地选择出敏感性的参数，为下一步优化做准备。而对于采样次数的影响，本研究认为，需要先对不同的采样次数做计算，一直到敏感性结果趋于收敛，这才是最终的敏感性结果，这就消除了采样次数对敏感性结果的影响。

3.2马尔科夫蒙特卡洛参数优化

通过敏感性筛选结果，选择了WOFOST模型中11个对叶面积和干物质影响大的参数作为优化对象，设计3种校正-验证方案。从结果看，3种方案得到的参数输入模型，模型都较好地模拟了观测值。从3种优化方案的参数结果看，3套参数都趋于稳定，这也说明马尔科夫蒙特卡洛方法可以较为稳定地反演出最优的参数，证实这套方法用在WOFOST模型调参的可行性。从模型验证来看，模型对潜在水平的模拟比雨养下的要好，这可能和WOFOST的模型结构有关，雨养水平下，WOFOST模型把土壤水分循环模块添加了进来，而对于潜在产量水平，模型默认是把土壤一直是处于田间持水量的状态。雨养情况下模型的复杂度比潜在情况下要复杂，且由于降水少，作物生长处于水分胁迫的时候多，由此可见模型对于水分胁迫的模拟是不足的，类似的研究在CERES模型中也见有报道[2]。

对于非线性优化的过程中，优化收敛性对初值非常敏感。如果初始值选择不好，有时候可能很难达到收敛。为了减少初值给优化带来的收敛性难的问题，本研究采取的策略是先手动粗略地调整参数，使模拟趋势大致差不多时的参数作为初始值。这可以减少收敛性带来的不确定性。参数的确定，依赖于观测数据，当观测数据样本能够较好地反应总体时，估计得到的参数就越准确，也能够避免“异参同效”的现象[30]。在反演品种参数的过程中，能有较多年份的观测数据对反演品种参数是有帮助的。MCMC算法获得参数的后验分布而不是一组唯一的最优参数解，一般认为最优那一组参数，是对应的似然函数值最大的那一套参数。各个参数的后验平均值作为一套品种参数，这套品种参数并不一定是最优的那一套品种参数。但是这个均值和MCMC获得的参数最大后验概率对应参数较为接近，说明参数分布是朝着高概率区进行收敛。

相比传统的试错法，本研究中的马尔科夫蒙特卡洛方法对WOFOST参数的自动优化方法，更具客观性。与之其他的调参研究[1-2]，本研究在调参之前进行的参数敏感性分析，可以有的放矢地选择最敏感的参数，一来可以减少优化参数的个数，二来也可以正确地选择优化对象。

4　结　论

本研究，运用栾城1998－2001年3个生育期的冬小麦在全灌溉和雨养的田间数据，对WOFOST模型55个参数进行了潜在生长、雨养生长水平下的参数全局敏感性分析，筛选出11个对叶面积和干物质影响最大的参数，运用马尔科夫蒙特卡洛（Markov Chain Monte Carlo，MCMC）方法，设计了3种校正-验证方案，得到的结论如下：

1）在WOFOST冬小麦的55个作物参数中，对叶面积影响最大的参数为：生育期为0时的比叶面积（SLATB00）、生育期为0.5时的比叶面积（SLATB050）、生育期为0.6时的比叶面积（SLATB060）、生育期为0.75时的比叶面积（SLATB075）、生育期为1.5时的最大光合速率（AMAXTB150）、叶面积指数最大增长率（RGRLAI）。对地上干物质影响较大的参数为：生育期为1.5时的最大光合速率（AMAXTB150）、生育期为0时的比叶面积（SLATB00）、35℃时叶面积的生命周期（SPAN）、生育期为0时的散射消光系数（KDIFFTB00）、生育期为1.8时的最大光合速率（AMAXTB180）、储存器官的同化物转换效率（CVO）。

2）潜在和雨养产量水平下，最大叶面积和地上生物量对参数的敏感性差异不大。

3）马尔科夫蒙特卡洛方法（MCMC）可以对WOFOST模型品种参数较好地优化，设计的三种校正-验证方案中，第一种方案（用1998－1999年的数据作为校正年份，1999－2000年，2000－2001年的数据作为验证年份）模拟效果最好。其中对潜在产量水平的叶面积和生物量的模拟，一致性指数d都大于0.9；对雨养产量水平的叶面积和生物量的模拟，一致性指数d＞0.75。

4）优化后的参数，相比有水分胁迫的雨养的生长情况，WOFOST在潜在的生长水平下模拟较好。

[参考文献]

[1] 房全孝. 根系水质模型中土壤与作物参数优化及其不确定性评价[J]. 农业工程学报，2012，28（10）：118－23. Fang Quanxiao. Optimizing and uncertainty evaluation of soil and crop parameters in root zone water quality model[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2012， 28（10）: 118－123. （in Chinese with English abstract）

[2] 姚宁，周元刚，宋利兵，等. 不同水分胁迫条件下DSSAT-CERES-Wheat模型的调参与验证[J]. 农业工程学报，2015，31（12）：138－150. Yao Ning， Zhou Yuangang， Song Libing， et al. Parameter estimation and verification of DSSAT-CERES-Wheat model for simulation of growth and development of winter wheat under water stresses at different growth stages[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2015， 31（12）: 138－150. （in Chinese with English abstract）

[3] Wang Q J. The genetic algorithm and its application to calibrating conceptual rainfall-runoff models[J]. Water Resourses Research， 1991， 27（9）: 2467－71.

[4] Beven K， Binley A. The future of distributed models: Model calibration and uncertainty prediction[J]. Hydrological Processes， 1992， 6（3）: 279－298.

[5] He Jiangqiang， Dukes， M D， Jones， J W， et al. Applying GLUE for estimating CERES-Maize genetic and soil parameters for sweet corn production[J]. Transactions of the ASABE， 2009， 52（6）: 1907－1921.

[6] He Jiangqiang， Jones， J.W.， Graham W.D.， et al. Influence of likelihood function choice for estimating crop model parameters using the generalized likelihood uncertaintyestimation method[J]. Agricultural Systems， 2010， 103（5）: 256－264.

[7] Iizumi T， Yokozawa M， Nishimori M. Parameter estimation and uncertainty analysis of a large-scale crop model for paddy rice: Application of a Bayesian approach[J]. Agricultural and Forest Meteorology， 2009， 149（2）: 333－348.

[8] van Oijen M， Cameron D R， Butterbach-Bahl K， et al. A Bayesian framework for model calibration， comparison and analysis: Application to four models for the biogeochemistry of a Norway spruce forest[J]. Agricultural and Forest Meteorology， 2011， 151（12）: 1609－1621.

[9] van Oijen M， Reyer C， Bohn F J， et al. Bayesian calibration，comparison and averaging of six forest models， using data from Scots pine stands across Europe [J]. Forest Ecology and Management， 2013， 289: 255－268.

[10] Tao Fulu， Yokozawa M， Zhang Zhao. Modelling the impacts of weather and climate variability on crop productivity over a large area: a new process-based model development，optimization， and uncertainties analysis[J]. Agricultural and Forest Meteorology， 2009， 149（5）: 831－850.

[11] Makowski D， Wallach D， Tremblay M. Using a Bayesian approach to parameter estimation: comparison of the GLUE and MCMC methods[J]. Agronomie， 2002， 22（2）: 191－203.

[12] Wang Jing， Li Xin， Lu Ling， et al. Parameter sensitivity analysis of crop growth models based on the extended Fourier Amplitude Sensitivity Test method[J]. Environmental Modelling ＆ Software， 2013， 48: 171－182.

[13] 何亮，赵刚，靳宁，等. 不同气候区和不同产量水平下APSIM-Wheat模型的参数全局敏感性分析[J]. 农业工程学报，2015，31（14）：148－157. He Liang， Zhao Gang， Jin Ning， et al. Global sensitivity analysis of APSIM-Wheat parameters in different climate zones and yield levels[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE），2015， 31（14）: 148－157. （in Chinese with English abstract）

[14] 黄敬峰，陈拉，王秀珍. 水稻生长模型参数的敏感性及其对产量遥感估测的不确定性[J]. 农业工程学报，2012，28（19）：119－129. Huang Jingfeng， Chen La， Wang Xiuzhen. Sensitivity of rice growth model parameters and their uncertainties in yield estimation using remote sensing date[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2012， 28（19）: 119－129. （in Chinese with English abstract）

[15] 姜志伟，陈仲新，周清波，等. CERES-Wheat 作物模型参数全局敏感性分析[J]. 农业工程学报，2011，27（1）：236－242. Jiang Zhiwei， Chen Zhongxin， Zhou Qingbo， etal. Global sensitivity analysis of CERES-Wheat model parameters[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2011， 27（1）: 236－242. （in Chinese with English abstract）.

[16] 宋明丹，冯浩，李正鹏，等. 基于Morris 和EFAST 的CERES-Wheat 模型敏感性分析[J]. 农业机械学报，2014，45（10）：124－131. Song Mingdan， Feng Hao， Li Zhengpeng， et al. Global sensitivity analyses of DSSAT-CERES-wheat model using morris and EFAST Methods[J]. Transactions of the Chinese Society for Agricultural Machinery （Transactions of the CSAM）， 2014， 45（10）: 124－131. （in Chinese with English abstract）.

[17] 吴锦，余福水，陈仲新，等. 基于EPIC 模型的冬小麦生长模拟参数全局敏感性分析[J]. 农业工程学报，2009，25（7）：136－142. Wu Jin， Yu Fushui， Chen Zhongxin， et al. Global sensitivity analysis of growth simulation parameters of winter wheat based on EPIC model[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE），2009， 25（7）: 136－142. （in Chinese with English abstract）.

[18] 王会肖，刘昌明. 作物水分利用效率内涵及研究进展[J].水科学进展，2000，11（1）：99－104. Wang Huixiao， Liu Changming. Advances in crop water use eff ic iency research[J]. Advances in Water Sceience， 2000，11（1）: 99－104. （in Chinese with English abstract）.

[19] Zhang Yongqiang， Kendy E， Yu Qiang， et al. Effect of soil water deficit on evapotranspiration， crop yield， and water use efficiency in the North China Plain[J]. Agricultural Water Management， 2004， 64（2）: 107－122.

[20] Chen Chao， Wang Enli， Yu Qiang. Modeling wheat and maize productivity as affected by climate variation and irrigation supply in north China Plain[J]. Agronomy Jounal，2010， 102（3）: 1037－1049.

[21] Chen Chao， Wang Enli， Yu Qiang， et al. Quantifying the effects of climate trends in the past 43 years （1961－2003） on crop growth and water demand in the North China Plain[J]. Climatic Change， 2010， 100（3/4）: 559－578.

[22] Chen Chao， Wang Enli， Yu Qiang. Modelling the effects of climate variability and water management on crop water productivity and water balance in the North China Plain[J]. Agricultural Water Management， 2010， 97（8）: 1175－1184.

[23] 马玉平，王石立，张黎. 针对华北小麦越冬的WOFOST模型改进[J]. 中国农业气象，2005，26（3）：145－149. Ma Yuping， Wang Shili， Zhang Li. Study on improvement of WOFOST against overwinter of wheat in north China[J]. Chinese Journal of Agrometeorology， 2005， 26（3）: 145－149. （in Chinese with English abstract）

[24] 邬定荣，欧阳竹，赵小敏，等. 作物生长模型WOFOST在华北平原的适用性研究[J]. 植物生态学报，2003，27（5）：594－602. Wu Dingrong， Ou Yangzhu， Zhao Xiaoming， et al. The applicability reseracher of WOFOST model in North China Plain[J]. Acta Phytoecologica Sinia， 2003， 27（5）: 594－602. （in Chinese with English abstract）.

[25] Saltelli A， Tarantola S， Campolongo F， et al. Sensitivity analysis in practice: a guide to assessing scientific models[M]. John Wiley and Sons， 2004: 20－78.

[26] 曹飞凤. 基于MCMC方法的概念性流域水文模型参数优选及不确定性研究[D]. 杭州：浙江大学，2010：16－25. Cao Feifeng. Study on Paramater Optimization and Uncertainty Analysis for Concenptual Hydrological ModelBase on MCMC Method[D]. Hangzhou: Zhejiang University，2010: 16－25. （in Chinese with English abstract）

[27] 茆师松，汤银才. 贝叶斯统计[M]. 北京：中国统计出版社，2012.

[28] Ceglar A， Črepinšek Z， Kajfež-Bogataj L， et al. The simulation of phenological development in dynamic crop model: The Bayesian comparison of different methods[J]. Agricultural and Forest Meteorology， 2011， 151（1）: 101－115.

[29] Zhao Gang， Bryan B A， Song Xiaodong. Sensitivity and uncertainty analysis of the APSIM-wheat model: Interactions between cultivar， environmental， and management parameters[J]. Ecological Modelling， 2014， 279: 1－11.

[30] 吕尊富，刘小军，汤亮，等. 基于WheatGrow和CERES模型的区域小麦生育期预测与评价[J]. 中国农业科学，2013，46（6）：1136－1148.

Lu Zunfu， Liu Xiaojun， Tang Liang， et al. Regional prediction and evaluation of wheat phenology based on the WheatGrow and CERES models[J]. Scientia Agricultura Sinica， 2013， 46（6）: 1136－1148. （in Chinese with English abstract）

Parameters optimization of WOFOST model by integration of global sensitivity analysis and Bayesian calibration method

He Liang1, Hou Yingyu1, Zhao Gang2, Wu Dingrong3, Yu Qiang4,5
（1. Nɑtionɑl Meteorologicɑl Center， Beijing 100081， Chinɑ;2. Crop Science Group， Institute of Crop Science ɑnd Resource Conservɑtion （INRES）， University of Bonn， Kɑtzenburgweg 5， D-53115 Bonn， Germɑny;3. Chinese Acɑdemy of Meteorologicɑl Sciences， Beijing 100081，Chinɑ;4. Key Lɑborɑtory of Wɑter Cycle ＆ Relɑted Lɑnd Surfɑce Processes， Institute of Geogrɑphic Sciences ɑnd Nɑturɑl Resources Reseɑrch， University of Chinese Acɑdemy of Science， Beijing 100101， Chinɑ;5. School of Life Sciences， University of Technology Sydney，PO Box 123， Broɑdwɑy， NSW， 2007， Austrɑliɑ）

Abstract:Crop model calibration and validation are essential for model evaluation and application. It is important for model application to accurately estimate the values of crop model parameters and further improve the capacity of model prediction. In the previous researches， trial-and-error method was widely used in model calibration and validation. The deficiency of this method was subjective selection of parameter values and time-consuming processes. To overcome these issues， the optimization methods such as general likelihood uncertainty estimation （GLUE）， genetic algorithm （GA） and shuffled complex evolution （SCE-UA） algorithm were alternative method for model calibration and validation. However， it is a problem to decide which parameters for optimization. It is essential to select the most sensitive parameters among hundreds of parameters in the crop model for optimization. To avoid subjective selection of parameters for calibration and validation， we used the global sensitivity analysis method of model parameters and the Markov Chain Monte Carlo （MCMC） method based on Bayesian theory to optimize the crop genetic parameters in the WOFOST （world food studies）， and the data of three-year winter wheat field experiment in Luancheng in the North China Plain were adopted. The main objectives were: 1） to analyze the sensitivity and uncertainty of WOFOST brought by 55 crop genetic parameters using the extended Fourier amplitude sensitivity test; 2） to calibrate and validate the WOFOST using the MCMC method after sensitivity analysis. We found that: 1）The most sensitive parameters for maximum leaf area index （MAXLAI） in the crop growth period were successively: specific leaf area at development stage of 0， 0.5， 0.6， and 0.75， maximum CO2assimilation rate at development stage of 1.5， and maximum relative increase in LAI （RGTLAI）; 2） The most sensitive parameters for total above ground production （TAGP） in the crop growth period were successively: maximum CO2assimilation rate at development stage of 1.5 （AMAXTB150），specific leaf area at development stage of 0 （SLATB00）， life span of leaves growing at 35oC， extinction coefficient for diffuse visible light at development stage of 0 （KDIFFTB00）， maximum CO2assimilation rate at development stage of 1.8 （AMAXTB180）， efficiency of conversion into storage organs （CVO）; 3） The parameter sensitivity for MAXLAI and TAGP in potential and rain-fed production level was almost coincident， which indicated that yield level didn’t influence the parameter sensitivity results; 4） Eleven sensitive parameters were selected for optimization by using the MCMC method. The first calibration and validation strategy （i.e. the data in 1998-1999 for calibration and those in 1999-2000 and 2000-2001 for validation）， was better than other 2 strategies. 5） WOFOST simulation was much improved if the optimized parameters by the MCMC method were adopted. The index of agreement was higher than 0.9 and the relative root mean square error was less than 20%. However， WOFOST performed worse in rain-fed case because water stress factor was added to limit crop growth. The results indicate that more sensitive parameters should have priority in adjusting values for model calibration and validation. In addition， the MCMC method is a feasible optimization method for WOFOST calibration and validation.

Keywords:models; crops; optimization; WOFOST; global sensitivity; MCMC; model parameters optimization

作者简介：何亮，男（汉族），湖南永兴县人，博士，主要从事作物模型、农业气象和全球变化研究。北京国家气象中心，100081。

基金项目：公益性行业（气象）科研专项（GYHY201306052，GYHY201506001）

收稿日期：2015-11-13

修订日期：2015-12-21

中图分类号：S512.1

文献标志码：A

文章编号：1002-6819（2016）-02-0169-11

doi：10.11975/j.issn.1002-6819.2016.02.025