基于WinSRFR模拟灌溉农田土壤入渗参数年变化规律

蔡焕杰，徐家屯，王　健，陈新明，朱大炯，谢　菲（1.西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100；　2.西北农林科技大学中国旱区节水农业研究院，杨凌712100；　3.西北农林科技大学水利与建筑工程学院，杨凌 712100）



基于WinSRFR模拟灌溉农田土壤入渗参数年变化规律

蔡焕杰，徐家屯，王健，陈新明，朱大炯，谢菲
（1.西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100；2.西北农林科技大学中国旱区节水农业研究院，杨凌712100；3.西北农林科技大学水利与建筑工程学院，杨凌 712100）

摘要：土壤入渗参数是确定地面灌溉灌水技术参数的主要依据之一，而农田土壤入渗特性随着灌水与耕作存在着周期性变化。为了探究这种周期性变化规律，在冬小麦-夏玉米轮作体系下，基于泾惠渠灌区2012－2015年不同灌水时期的灌水资料，利用WinSRFR4.1软件与拟合度检验相结合的方法对考斯加科夫土壤入渗模型参数值进行模拟反推得出最佳优化结果，结果表明模拟与实测的水流推进及水流消退过程的均方根误差分别为0.15～2.1和2.5～7.8 min，决定系数均在0.7以上（P＜0.05）。在此基础上，根据影响土壤水分入渗的主导因素土壤容重及土壤质量含水率，建立考斯加科夫土壤水分入渗模型2参数值与影响因素间的定量关系，分析土壤入渗参数在年内的变化规律，结果表明：在冬小麦-夏玉米轮作体系下，不同灌水时期的土壤入渗系数和入渗指数变化明显，变化范围分别在95.0～210.0 mm/h和0.42～0.67之间，土壤水分入渗模型两参数值与土壤含水率及土壤表层容重之间存在较好地复合对数关系，决定系数分别为0.846和0.741 （P＜0.05）。研究结果可为年内不同灌水时期确定农田地面灌水技术参数提供依据。

关键词：入渗；模型；土壤水分；冬小麦-夏玉米；综合糙率系数

蔡焕杰，徐家屯，王健，陈新明，朱大炯，谢菲. 基于WinSRFR模拟灌溉农田土壤入渗参数年变化规律[J]. 农业工程学报，2016，32（2）：92－98.doi：10.11975/j.issn.1002-6819.2016.02.014http://www.tcsae.org

Cai Huanjie， Xu Jiatun， Wang Jian， Chen Xinming， Zhu Dajiong， Xie Fei. Yearly variation of soil infiltration parameters in irrigated field based on WinSRFR4.1[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE），2016， 32（2）: 92－98. （in Chinese with English abstract）doi：10.11975/j.issn.1002-6819.2016.02.014http://www.tcsae.org

0　引　言

土壤入渗是农田水循环中的一个重要环节，它是田间灌溉水、雨水等通过地表向下运移进入土壤并在土壤中进行运动和存储，从而形成土壤水的过程[1]。土壤的入渗特性决定着灌溉水或雨水转化为土壤水的速度和分布状况。而土壤水分入渗能力的大小则表现为土壤入渗参数值的不同，它是合理确定农田灌溉技术参数的基础指标之一[2-4]。影响大田土壤水分入渗特性的因素主要有土壤质地、土壤结构、土壤含水量和土壤有机质等[5-6]，国内外学者对其进行了大量的研究[7-11]。由于土壤本身的理化属性会在气象、农业技术措施、灌溉等因素的作用下发生变化，即土壤理化性质的时间变异性[12]，表现为耕作层土壤容重及土壤含水量的时间变异性，从而决定了土壤入渗特性也存在着时间变异性。通过研究不同灌水时期土壤入渗参数的变化规律，可以为年内不同时期灌水技术参数的确定提供依据，从而保证农业灌溉的灌水质量，实现节约用水、科学用水的目的。

土壤入渗特性研究大多是利用双环入渗仪进行土壤点状入渗试验，供试面积小，结果往往具有明显的点状或局部特征，受土壤特性空间变异性的影响，难以反映小区整体的变异情况[13-16]。因此，近年来国内外学者在确定土壤水分入渗参数时，多采用大田试验中的水流推进及消退资料进行推求。本文采用国内外常用的地面灌溉综合模拟软件WinSRFR4.1模型，依据田间水流推进及消退数据资料，对入渗参数进行模拟反推并利用拟合度检验得出最佳优化结果。在此基础上根据影响土壤水分入渗的主导因素，即耕作层土壤容重及土壤含水量，建立土壤水分入渗模型参数值与影响因素间的定量关系，探求入渗参数在一个耕作周期内的变化规律。

1　材料与方法

1.1试验区概况

试验在位于陕西省关中平原中部的泾惠渠灌区进行（108°34′34″～109°21′35″E、34°25′20″～34°41′40″N），东西长约70 km，南北宽约20 km。目前该灌区灌溉面积约9.7万hm2，有效灌溉面积约8.8万hm2，为关中九大灌区之一的大（Ⅱ）型灌区。该地区海拔450～350 m，地面坡降 0.003～0.0016。年平均降水量535 mm，降水时空分布极不均匀，7－9月降水量占年降水总量的50%～60%，年蒸发量1 212 mm左右。该地区土壤类型为塿土，田间持水量约为23.5%（质量含水量），土壤物理参数见表1。

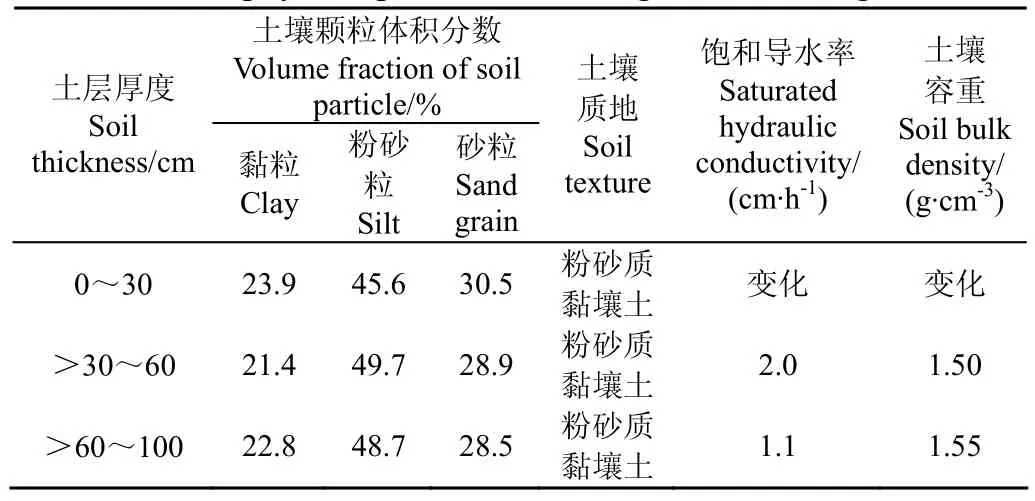
表1　泾惠渠灌区土壤物理参数表Table 1　Soil physical parameters of Jinghui Canal irrigation area

1.2田间灌溉试验设计

试验区面积约2 hm2，设计不同的畦田长度分别为80、120、235 m，畦宽在2.3～4.8 m之间，试验田块具体设计见文献[17]。作物种植模式为夏玉米-冬小麦轮作（夏玉米生长时期为6－10月，冬小麦生长时期为10－6月），冬小麦种植品种为西农979，夏玉米种植品种为武科2号。

畦灌试验时间为2012年10月－2015年6月。其中，2012年灌水1次，灌水日期为11月16日；2013年灌水5次，灌水日期分别为1月18日、3月8日、6月16日、8月16日、10月20日；2014年灌水5次，灌水日期分别为1月11日、4月2日、6月16日、7月25日、11 月3日，2015年灌水2次，灌水日期分别为1月14日、3月11日。

试验前分别测量每个畦田的宽度、坡度，灌水时分别测量入畦流量、畦田内水流推进、消退和水深等参数，灌水前后测量土壤质量含水率以及0～30 cm土壤容重。

1.3测定方法

1）畦宽及坡度的测量：每块畦田的宽度用卷尺进行测量记录，畦田坡度通过水准仪测高程计算得到。

2）耕作层土壤质量含水率θm及土壤容重γd测量：单次灌水前后，分别于畦田首、中、尾3个断面，用取土烘干法测量土壤质量含水率θm，并在同样位置用环刀对耕作层土壤0～30 cm厚度取土并烘干测量土壤表层容重γd。

3）流量测量：灌水过程中利用LS45A型旋杯式流速仪在农渠上进行流速测量，并利用农渠断面面积进行流量测算。

4）田面水流推进、消退数据和畦首处水深的测量：灌水前，沿畦田灌水方向每隔10 m插1面小旗子进行田面水流推进及消退过程观测，并于畦首处设1个水尺，进行畦首地表水深观测；灌水过程中采用秒表计时，记录水流前锋每推进至1面小旗子的时间，作为水流推进数据，同时记录畦首处水深；灌水结束后，从畦首开始水流每消退至1面小旗子处，记录消退时间。

由于试验区面积较大，各个地块之间不同程度上存在着空间变异性，为了分析入渗参数的年变化规律，经过试验数据分析，选取空间变异性较小的地块（即编号20-1～24-2的10块地）作为试验分析地块，并取2013 年6月－2015年6月2 a的数据进行分析，2012年10月－2013年6月的试验数据作为验证。

2　基于WinSRFR4.1土壤入渗参数的优化求解

2.1WinSRFR4.1模型介绍

WinSRFR4.1模型是美国水保实验室开发的一维地面灌溉模拟模型，它是集地面灌溉评价、设计和模拟为一体的综合性分析软件[18-19]。WinSRFR4.1软件包括4部分：1）利用实测的田间灌水试验数据（水流推进、消退数据等）推求土壤入渗参数、田面糙率系数以及对灌水质量进行综合评价的灌溉分析评价模块（event analysis）；2）利用土壤水分入渗参数以及灌溉技术要素对明渠非恒定流方程进行求解的水力学模拟模块（hydraulic simulation）；3）对田块几何参数进行优化设计，使其具有较高灌水质量的灌溉系统设计模块（physical design）；4）对于给定的田块规格，进行入流量和关口时间的优化从而达到较高灌水质量的灌溉运行管理模块（operations analysis）。

本文采用WinSRFR4.1模型中的灌溉分析评价模块进行土壤入渗参数的优化反求。该模型提供了2种推求方法：1）根据水量平衡原理，由实测的水流推进及消退数据对入渗参数进行反求（Merriam-Keller post-irrigation volume balance analysis）；2）采用田间两点法，即仅仅依据沿畦长方向的2个位置的水流推进实测数据进行土壤入渗参数估算（Elliot-Walker two-point method analysis）。由于两点法波动性较大，因此本文采用第1种方法对土壤入渗参数进行优化反求，并在模拟地面灌溉水流运动过程中，选用零惯量模型[20]。

2.2土壤入渗参数的优化求解

大田土壤入渗过程可用考斯加科夫入渗模型 It＝K·tα来描述[10]，其中t为受水时间；It为t时刻土壤累计入渗量，mm；K为经验入渗系数；α为经验入渗指数。该模型模拟结果与实际入渗过程吻合度较好[21]，本次研究运用考斯加科夫入渗模型模拟大田入渗过程。求解入渗模型参数值时采用WinSRFR4.1中的田间灌水试验分析模块进行优化求解[22]。

首先，利用曼宁公式[17，23]求解得出田面综合糙率系数：

式中n为田面综合糙率系数；J为田块坡度，m/m；h为畦首处水深，m；q为田间实测单宽流量，L/（s·m）。

然后，根据田间实测的水流推进、消退资料及相关的基础田间数据，利用灌水试验分析模块中的Merriam-Keller法进行反复模拟，直至模拟的田面水流推进和消退过程与实测数据达到较高吻合程度，即模拟值与实测值拟合度较好，从而得到相应的入渗系数K和入渗指数α。

为了使WinSRFR4.1模型模拟的入渗参数及入渗指数值能够更加准确地反映田间实际情况，需要对模型所模拟的以及田间实测的水流推进及水流消退数据进行拟合度检验，本文在对模型模拟的过程中采用归一化误差（均方根差/平均值）进行参数优化，通过反复模拟以减小模拟结果与实测结果的差异，当归一化误差数值最小时所得到的入渗系数以及入渗指数值作为最终的优化结果。在模拟过程中采用均方根差（root mean square error，RMSE）和决定系数R2来评价模型的模拟效果。

3　结果与分析

3.1耕作层土壤容重及质量含水率的变化

图1为2013年6月－2015年6月冬小麦-夏玉米轮作体系下不同灌水时期以及降雨前后测量的耕作层土壤容重及土壤质量含水量的变化。主要受土粒密度和土壤孔隙2方面的影响，土壤容重本质上则是土壤紧实程度的间接反映，从而一定程度上影响了农田土壤水分入渗性能；田间土壤质量含水率的变化导致了湿润区内入渗水流平均势梯度的不同，在一定程度上影响了农田土壤水分入渗性能。

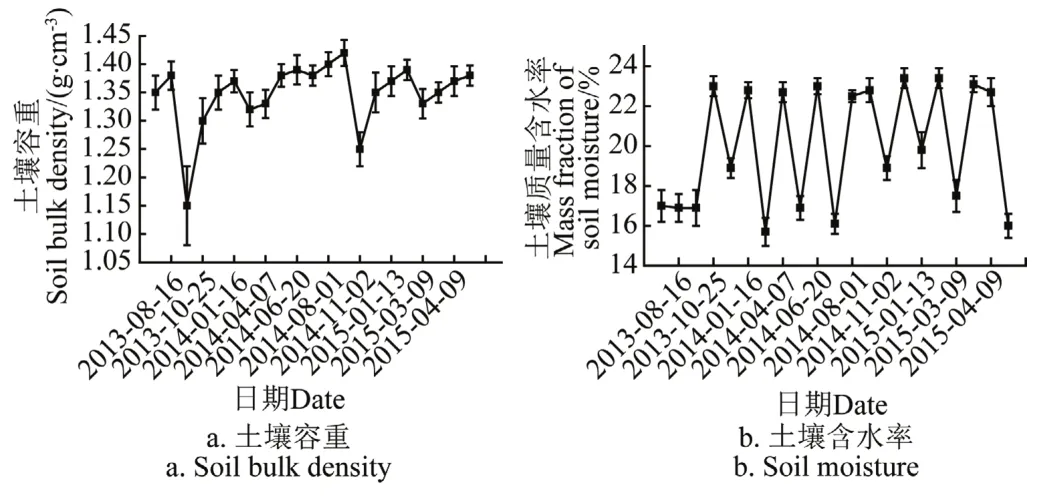
图1　冬小麦-夏玉米轮作体系下不同时期耕作层0～30 cm土壤容重及质量含水量变化图Fig.1　Changes of soil bulk density and water content in different periods of 0-30 cm soil depth of winter wheat-summer maize rotation system

玉米播种方式是留茬免耕播种，对地表土壤结构破坏性较小，经过前期小麦地灌水降雨等压实作用，因此玉米地有较紧实、稳定的土壤结构，耕作层土壤容重较大。由图1a中看出，此时期（2013年6月15日）玉米耕作层土壤容重达到1.35 g/cm3，土壤质量含水率约为17%，为了保证玉米正常出苗率，2013年6月16日进行了玉米第1水灌溉。而此后时期干旱少雨，玉米遮阴率低，表土较易形成干土层，此时期土壤水分的消耗主要是在干土层以下的界面以水汽扩散的形式进行，耕作层土壤结构相对保持稳定，容重变化不大。之后又经过几次降雨的压实作用，因此到第2次灌溉前（2013年8月15日），耕作层土壤容重增加至1.38 g/cm3，土壤质量含水率约为16.9%。2013年10月初玉米收割后，由于实行了秸秆还田以及土壤深翻等农艺措施，使得小麦前期耕作层土壤结构遭到破坏，变得比较疏松。到小麦第1次灌水前（2013年10月17日）耕作层土壤容重达到最小值为1.15 g/cm3。2013年10月20日进行了小麦第1次灌水，此时土壤耗水较大，灌溉过程中地表土壤结构再次被破坏。小麦耕作层土壤逐渐密实，灌水过后（2013年10月28日）土壤容重增加至1.29 g/cm3。且随着后续的几次降雨对地表的压实作用，耕作层土壤容重持续增大，到冬灌前（2014年1月8日）达到1.35 g/cm3，此时土壤质量含水率为19%。为了保证冬小麦能够顺利越冬，2014年1月初，对冬小麦进行了第2次灌水处理，灌水过后土壤容重稍稍增加。随后小麦地表温度逐渐降低，蒸发蒸腾降至最低。春天表土层逐渐升温，加之小麦返青后根系生长较快，使得耕作层土壤容重较之前有所减小。这段时期小麦地水分消耗主要以植株蒸腾为主，且降雨较少，地表很难形成较厚的干土层，结构较为稳定，到第3次灌水（2014年4月1日）前，耕作层土壤容重为1.32 g/cm3。之后经过了一段长时间的持续降雨，对耕作层土壤的压实作用较为明显，降雨结束后（2014年6月2日）土壤容重增加至1.38 g/cm3，2014年6月初冬小麦收获。2014年6月－2015年6月进行了第2年试验，土壤结构变化规律与第1年变化类似。特别说明的是，由于夏玉米后期降雨时间较长，降雨量较大，夏玉米收获时，土壤含水率较大，冬小麦采用了浅耕播种技术，此时耕作层土壤容重较前1年有所增大。

3.2土壤入渗参数的优化求解结果

3.2.1模型率定

不同灌水时期田间耕作层土壤容重及土壤含水率的不同导致了不同时期土壤入渗参数值的差异，直观反映在畦田地面水流推进及水流消退过程中，可利用畦田灌溉过程中水流推进及消退过程数据对不同灌水时期的土壤入渗参数值分别进行优化求解，通过研究不同灌水时期土壤入渗参数值的变化规律，为年内不同时期灌水技术参数的优化提供依据。以编号为20-1（畦长为120 m，畦宽为3 m，纵向坡度为0.0036 m/m）的田块为例进行土壤入渗参数值的优化模拟说明，如图2所示。

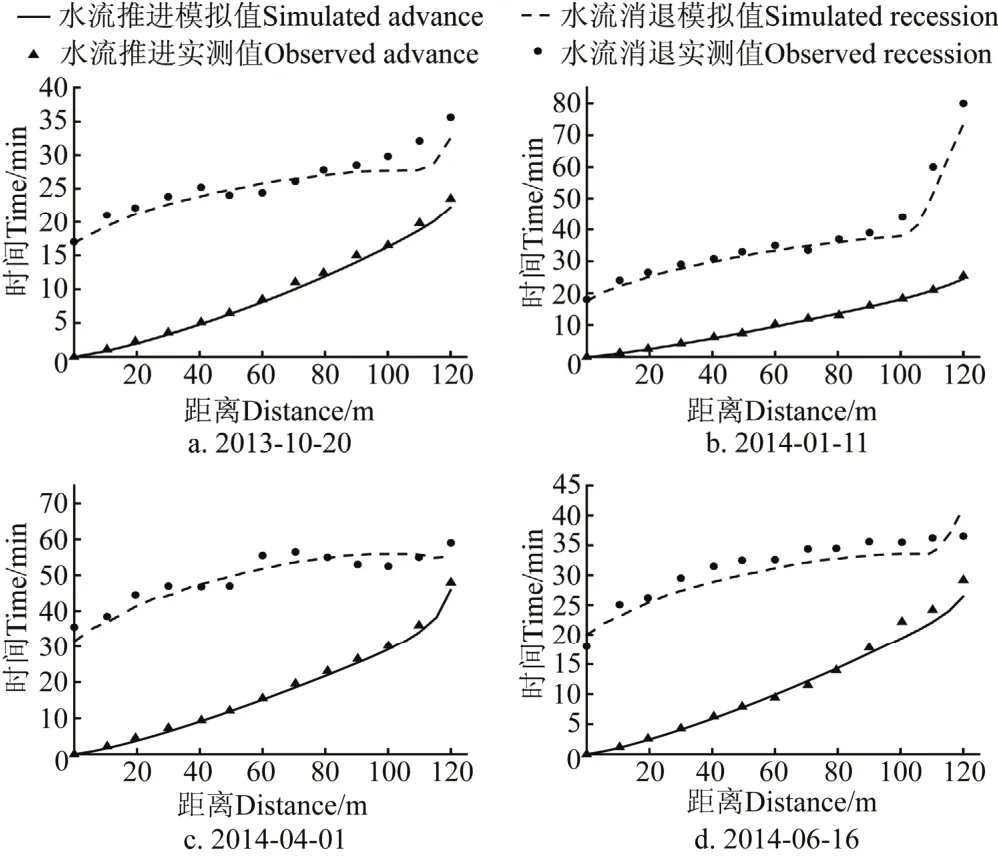
图2　编号20-1地块不同灌水时期水流推进与消退过程模拟值与实测值对比结果Fig.2　Comparisons of observed and simulated values of water flow advance and recession in different irrigation date of field 20-1

图2为利用WinSRFR4.1软件对该畦长不同灌水时期（2013年10月20日、2014年1月11日、2014年4月1日、2014年6月16日）优化出土壤入渗参数值，并通过拟合度检验使得归一化误差达到最小值时的水流推进与消退模拟值与实测值之间的对比。表2为该畦田土壤入渗参数值与糙率系数优化估算值以及拟合度检验表。由图2及表2可以看出，该畦田冬小麦春灌以及夏玉米压茬灌溉时，水流消退数据拟合度稍差，决定系数较小，可能的原因是春灌时期，冬小麦长势较旺，密度较大，观测到的水流消退数据较实际存在一定的误差，而夏玉米压茬水灌溉时，由于地表覆盖部分小麦秸秆，导致实际水流消退时受到一定影响，同时观测到的水流消退数据也存在着一定的误差。总体而言，该畦田4次灌水的水流推进与消退数据的模拟值与实测值吻合程度较好，拟合度较优，具有较好的一致性，说明WinSRFR4.1模型能够较好地反映出地面畦灌水流运动过程，优化模拟的入渗参数值较为合理可靠。利用此方法对其他田块不同灌水时期的入渗参数值进行拟合优化，最优结果表明水流推进模拟值与实测值均方根误差保持在0.15～2.1 min之间，水流消退模拟值与实测值均方根误差则保持在2.5～7.8 min之间，决定系数均在0.7以上，这与章少辉等[18]利用SGA和SRFR进行优化反演模型得出的结果类似，本研究优化结果较为可靠。

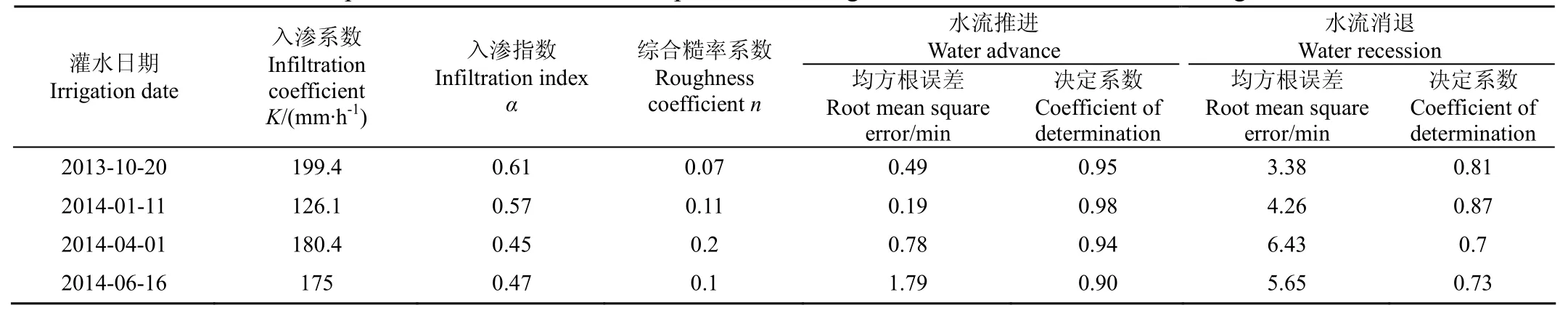
表2　20-1畦田不同灌水日期模拟优化土壤入渗参数值及拟合度检验Table 2　Optimization of soil infiltration parameters and goodness of fit tests of different irrigation date

3.2.2模型验证

取2012年10月－2013年6月冬小麦3次灌水的资料数据进行分析验证。由试验过程中所测得的耕作层土壤容重γd、质量含水率θm，根据上面拟合的考斯加科夫土壤入渗模型参数值的经验回归模型计算出K及α，将K 及α作为已知条件，利用WinSRFR软件模拟出地面水流推进及消退过程，再将实测的水流推进及消退数据与模拟数据进行对比分析，从而对经验回归模型的合理性进行反向验证。以编号为20-1的畦田为例进行经验回归模型的验证。

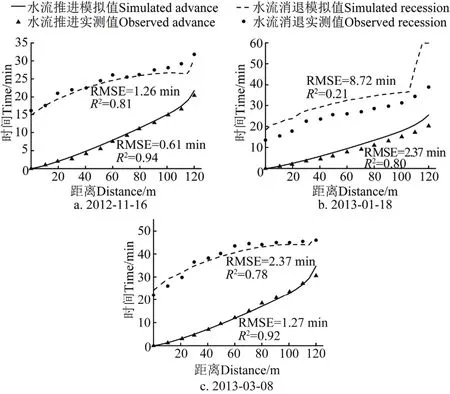
图3　20-1畦田不同灌水时期水流推进、消退模拟值与实测值对比验证Fig.3　Verification between simulated and measured values of water flow advance and recession in different irrigation periods for field 20-1

图3为编号20-1的畦田在不同灌水时期水流推进、消退模拟值与实测值对比验证图。根据所拟合得出的经验回归模型计算的考斯加科夫土壤水分入渗模型参数值作为已知条件，利用WinSRFR软件对2012年11月16日及2013年3月8日2次灌水所模拟的水流推进及消退数据与实测值总体拟合较好，2次水流推进及消退RMSE值分别达到了0.61、1.26和1.27、2.37 min，R2值分别达到了0.94、0.81和0.92、0.78，说明所拟合的考斯加科夫土壤入渗模型两参数值的经验回归方程是合理的，可较好地估算土壤入渗参数值。2013年1月18日一次拟合较差，水流推进及消退RMSE值为2.37 和8.72 min，R2值分别为0.80和0.21。该次模拟结果较差，可能的原因是此时土壤有1层较厚的冻土层，而冻结土壤水分的入渗率远小于未冻结土壤水分的入渗率[24]。2014年和2015年冬灌时，土壤并没有产生冻土层，因此拟合经验方程时并没有考虑冻土层对土壤入渗特性的影响，综合考虑冻土层对土壤入渗特性的影响还需进一步研究。

3.3入渗参数及其与耕作层土壤容重和质量含水率的关系分析

3.3.1入渗参数

为了分析不同灌水时期土壤入渗参数值的变异规律，选取了变异性较小的20-1～24-2的10块畦田进行分析。为了较为直观地比较该区域不同灌水时期土壤入渗参数值的平均变异程度，画出了考斯加科夫土壤入渗模型参数值的箱式分布图。图4为该区域不同灌水时期不同地块所模拟优化的考斯加科夫入渗模型参数K、α值箱式分布图，由图4可以看出不同灌水时期土壤入渗参数K及入渗指数α值差异性比较明显，平均变化范围分别在95.0～210.0 mm/h和0.42～0.67之间。因此，对影响入渗参数值的主要因子耕作层土壤容重以及土壤质量含水率进行不同灌水时期的土壤入渗参数值的影响分析。

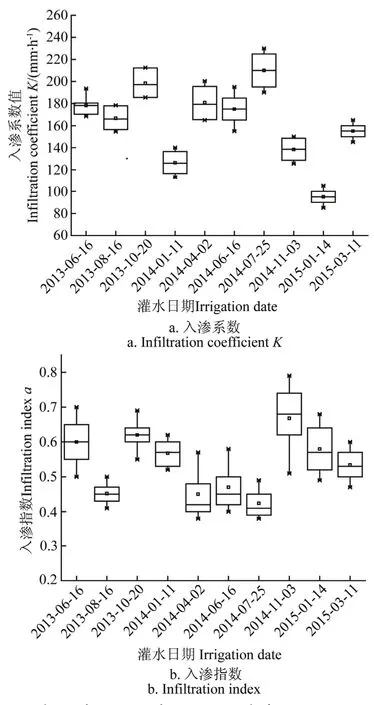
图4　泾惠渠灌区不同灌水时期入渗参数值箱式分布图Fig.4　Box-plot of soil infiltration parameters in different irrigation period in Jinghui Canal irrigation area

3.3.2入渗参数与耕作层土壤容重和质量含水率的关系分析

土壤入渗参数是确定地面灌溉技术参数的必要依据，而在1个耕作周期内，不同灌水时期，耕作层土壤容重γd、质量含水率θm变化差异较大，从而导致土壤入渗特性的差异性变大，这给不同灌水时期地面灌溉技术的优化带来了很大不便。而土壤入渗特性受到较多因素的影响，很难找到这些因素与土壤入渗参数值之间的理论关系，但我们可以依据试验结果，应用数理统计方法[25]建立考斯加科夫土壤入渗模型中2参数值K、α与土壤容重γd、质量含水率θm间的经验模型。因此，采用实测耕作层0～30 cm土壤容重γd、质量含水率θm与模拟优化的土壤入渗模型两参数值等资料进行二元非线性回归分析，并对其偏回归系数值进行了检验。回归分析及方程检验结果见表3。

由表3可以看出，考斯加科夫土壤入渗模型中2参数值与耕作层土壤容重及质量含水率的回归拟合较好，且两者的校正R2分别达到了0.8及0.7以上，表明该回归模型拟合度较高，适应性较好。土壤入渗模型中2参数值K、α与土壤容重γd、质量含水率θm的偏回归系数检验亦达到显著或极显著水平，即耕作层土壤容重以及土壤质量含水率的变化均会对土壤考斯加科夫入渗模型中2参数值的变化产生影响，说明此次研究将耕作层土壤容重及质量含水率作为影响土壤入渗参数值的主要影响因子是合理的。

表3　入渗参数与土壤容重、质量含水率之间回归方程及偏回归系数检验Table 3　Regression equation of soil infiltration parameters with soil bulk density and soil mass water content and partial regression coefficient correction

由表3回归方程关系式可以看出，随着土壤容重γd的增大，土壤入渗参数K值逐渐减小，α值逐渐减小，这与李卓等[10]、解文艳等[7]通过点状入渗法研究的结果相一致。耕作层土壤容重越小，即土壤结构越疏松，疏松土壤孔隙率比较大，连通性较好，对入渗水分运动的阻力较小，因而灌溉水进入田间后的第一个单位时间入渗量就大，表现为土壤入渗系数K值的增大。而对于较大的土壤容重，表现为土壤密实度增加，孔隙率减小，孔隙连通性差，表现为灌溉水进入田间后在第1个单位时间内入渗量小。所以随着土壤容重的增加，考斯加科夫入渗模型系数K值越小；α值的大小决定于由于土体湿润而引起的土壤结构的改变。大部分学者研究认为，在土壤质地不变的情况下α值保持不变。而在田间由于耕作措施以及灌溉、降雨等作用对耕作层土壤扰动较大，破坏了土壤本身的结构，因此，在土壤质地不变的情况下，由于土壤容重的变化也会导致经验入渗指数α的较大变化。李卓等[10]认为，容重较小的土壤，大孔隙较多，土壤内部连通性较好。当灌溉水进入田间，土粒遇水作用膨胀后，土壤孔隙内部的气体可以较快的排放出来，从而有效减小了入渗过程中的气相阻力，所以入渗能力的衰减速度减慢。

土壤入渗系数K值随土壤含水率的增大而减小，其可能原因是，在开始入渗后的很短时间内，水分很快会使地表一定厚度内的土壤达到准饱和，在过水面积一定的情况下，入渗通量取决于势梯度，而势梯度的大小主要取决于土壤含水率。土壤含水率越高，入渗水势梯度越小，入渗通量也就越小。因此，土壤含水率越高，则土壤经验入渗系数K值越小。相应的，当土壤含水率较大时，土壤内部孔隙率变小，土壤内部的连通性较差，气相阻力变大，入渗能力降低，水分填充土壤孔隙的能力降低，从而入渗能力的衰减速度相应的变小；当土壤含水率较小时，土壤内部孔隙率变大，入渗能力增大，水分将很快的填充到土壤内部孔隙中。之后，随着孔隙率变小，气相阻力增大，土壤入渗能力逐渐减小。因此，入渗能力的衰减速度随着土壤含水率的减小而增大，即α随着土壤含水率的增大而增大。

4　结　论

本文依据田间灌水资料，利用WinSRFR4.1及其拟合度检验对考斯加科夫土壤入渗模型2参数值进行优化求解的基础上，探讨了耕作层土壤容重、质量含水率对入渗模型2参数值的影响，建立了入渗模型2参数值与耕作层土壤容重、质量含水率的经验回归模型，得到如下主要结论：

1）在冬小麦-夏玉米轮作周期内，由于农耕、灌溉、降雨等因素的影响，耕作层土壤容重存在周期性变化特性，最小值出现在土地深翻冬小麦播种时为1.15 g/cm3，最大值则出现在夏玉米后期为1.35 g/cm3，并趋于稳定。

2）利用WinSRFR4.1软件与拟合度检验相结合的方法，通过测定田间水流推进、消退数据可以较好地模拟反演出考斯加科夫土壤入渗模型参数值的大小，水流推进及消退过程均方根误差分别在0.15～2.1 min以及2.5～7.8 min之间，决定系数R2均在0.7以上，模拟结果与实测结果吻合度较好；且在不同灌水时期，考斯加科夫土壤入渗模型2参数值差异性较大，变化范围分别在95.0～210.0 mm/h和0.42～0.67之间。

3）随着耕作层土壤容重的变化，考斯加科夫土壤入渗模型两参数值也随之变化。入渗系数K随着耕作层土壤容重γd的增大而递减，入渗指数α随着耕作层土壤容重γd的增加而升高，即土壤初始入渗能力随容重增大而降低，入渗能力衰减速度随容重增大而递增，两参数值均与耕作层土壤容重呈显著对数相关；土壤质量含水率对土壤入渗模型2参数值有显著影响，随着土壤质量含水率θm的增加，入渗系数K以及入渗指数α均减小，它们之间都较好的复合对数关系。

4）试验所得出的考斯加科夫土壤入渗模型两参数值的回归模型拟合度较好，校正R2值分别为0.846和0.741，由此可以在不同的灌水时期通过测量田间耕作层土壤容重γd以及土壤质量含水率θm的大小，确定考斯加科夫土壤入渗模型中的2参数值K及α，从而为不同时期的灌水技术优化提供依据。

[参考文献]

[1] Hillel D. Environmental Soil Physics[M]. New York: Academic Press， 1998.

[2] 雷志栋，杨诗秀，谢森传. 土壤水动力学[M]. 北京：清华大学出版社，1988：77－130.

[3] Zerihun D， Feyen J， Reddy J M. Sensitivity analysis of furrow-irrigation performance parameters[J]. Journal of Irrigation and Drainage， ASCE， 1996， 122: 49－57.

[4] Oyonarte N A， Mateos L， Palomo M J. Infiltration Variability in Furrow Irrigation[J]. Canadian Metallurgical Quarterly，2002， 128（1）: 26－33.

[5] 樊贵盛，李雪转，李红星. 非饱和土壤介质水分入渗问题[M].北京：中国水利水电出版社，2012：17－39.

[6] Franzluebbers A J. Water infiltration and soil structure related to organic matter and its stratification with depth[J]. Soil ＆ Tillage Research， 2002， 66（2）: 197－205.

[7] 解文艳，樊贵盛. 土壤结构对土壤入渗能力的影响[J]. 太原理工大学学报，2004，35（4）：381－384. Xie Wenyan， Fan Guisheng. Influence of soil structure on infiltration characteristics of soil[J]. Journal of Taiyuan University of Technology， 2004， 35（4）: 381－384. （in Chinese with English abstract）

[8] 解文艳，樊贵盛. 土壤含水量对土壤入渗能力的影响[J].太原理工大学学报，2004，35（3）：272－275. Xie Wenyan， Fan Guisheng. Influence of moisture content on infiltration characteristics in field soils[J]. Journal of Taiyuan University of Technology， 2004， 35（3）: 272－275. （in Chinese with English abstract）

[9] 郑秀清，樊贵盛. 土壤含水率对季节性冻土入渗特性影响的试验研究[J]. 农业工程学报，2000，16（6）：52－55. Zheng Xiuqing， Fan Guisheng. Influence of moisture content on infiltration characteristics in seasonal frozen and thawed soils[J]. Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE）， 2000， 16（6）: 52－55. （in Chinese with English abstract）

[10] 李卓，吴普特，冯浩，等. 容重对土壤水分入渗能力影响模拟试验[J]. 农业工程学报，2009，25（6）：40－45. Li Zhuo， Wu Pute， Feng Hao， et al. Simulated experiment on effect of soil bulk density on soil infiltration capacity[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2009， 25（6）: 40－45.（in Chinese with English abstract）

[11] 李雪转，樊贵盛. 土壤有机质含量对土壤入渗能力及参数影响的试验研究[J]. 农业工程学报，2006，22（3）：188－190. Li Xuezhuan， Fan Guishen. Influence of organic matter content on infiltration capacity and parameter in field soil[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2006， 22（3）: 188－190. （in Chinese with English abstract ）

[12] 冯锦萍，樊贵盛. 土壤水分入渗年变化特性的试验研究[J].太原理工大学学报，2003，34（1）：16－19. Feng Jinping， Fan Guisheng. Experimental study of yearly change of soil water infiltration characteristics[J]. Journal of Taiyuan University of Technology， 2003， 34（1）: 16－19. （in Chinese with English abstract）

[13] Eghball B， Schepers J S， Negahban M， et al. Spatial and temporal variability of soil nitrate and corn yield[J]. Agronomy Journal， 2003， 95（2）: 339－346.

[14] Veronese Junior V， Carvalho M P， Dafonte J， et al. Spatial variability of soil water content and mechanical resistance of Brazilian ferralsol[J]. Soil ＆ Tillage Research， 2006， 85（112）: 166－177.

[15] 董孟军，白美健，李益农，等. 地面灌溉土壤入渗参数及糙率系数确定方法研究综述[J]. 灌溉排水学报，2010，29（1）：129－132. Dong Mengjun， Bai Meijian， Li Yinong， et al. A Review on the methods of determining infiltration parameters and roughness coefficient for surface irrigation[J]. Journal of Irrigation and Drainage， 2010， 29（1）: 129－132. （in Chinese with English abstract ）

[16] 聂卫波，费良军，马孝义. 区域尺度土壤入渗参数空间变异性规律研究[J]. 农业机械学报，2011，42（7）：102－108. Nie Weibo， Fei Liangjun， Ma Xiaoyi. Spatial variability of infiltration parameters at the region scales[J]. Transactions of Chinese Society for Agricultural Machinery， 2011， 42（7）: 102－108. （in Chinese with English abstract）

[17] 李世瑶，蔡焕杰，陈新明. 基于主成分分析的畦灌质量评价[J]. 农业工程学报，2013，29（24）：86－93. Li Shiyao， Cai Huanjie， Chen Xinming. Evaluation of border irrigation performance based on principal component and correlation analyses[J]. Transactions of the Chinese Societyof Agricultural Engineering（Transactions of the CSAE）， 2013，29（24）: 86－93.（in Chinese with English abstract）

[18] 章少辉，许迪，李益农，等. 基于SGA和SRFR的畦灌入渗参数与糙率系数优化反演模型-模型运用[J]. 水利学报，2007，38（4）：402－408. Zhang Shaohui， Xu Di， Li Yinong， et al. Optimized inverse model used to estimate kostiakov infiltration parameters and manning’s roughness coefficient based on SGA and SRFR model: （II） Application[J]. Journal of Hydraulic Engineering，2007， 38（4）: 402－408. （in Chinese with English abstract）

[19] Bautista E， Clemmens A J， Strelkoff T S， et al. Analysis of surface irrigation systems with WinSRFR-Example application[J]. Agricultural Water Management， 2009， 96: 1162－1169.

[20] 聂卫波，费良军，马孝义. 畦灌灌水技术要素组合优化[J].农业机械学报，2012，43（1）：83－88. Nie Weibo， Fei Liangjun， Ma Xiaoyi. Optimization for combination of irrigation technique element for border irrigation[J]. Transactions of the Chinese Society of Agricultural Machinery， 2012， 43（1）: 83－88. （in Chinese with English abstract）

[21] Adindu Ruth U， lgbokwe kelechi K， Chigbu Timothy O， et al. Application of Kostiako’s infiltration model on the soils of Umudike， Abia State-Nigeria[J]. American Journal of Environmental Engineering， 2014， 4（1）: 1－6.

[22] 李佳宝，魏占民，徐睿智，等. 基于SRFR模型的畦灌入渗参数推求及模拟分析[J]. 节水灌溉，2014，2（1）：1－3. Li Jiabao， Wei zhanmin， Xu Ruizhi， et al. Border irrigation infiltration parameters calculation and simulation analysis based on SRFR model[J]. Water Saving Irrigation Journal，2014， 2（1）: 1－3. （in Chinese with English abstract）

[23] 王全九，王文焰，张江辉，等. 根据畦田水流推进过程水力因素确定Philip入渗参数和田面平均糙率[J]. 水利学报，2005，36（10）：125－128. Wang Quanjiu， Wang Wenyan， Zhang Jianghui， et al. Determination of Philip infiltration parameter and Manning roughness according to hydraulic factors in the advance of irrigation water[J]. Journal of Hydraulic Engineering， 2005，36（1）: 125－128. （in Chinese with English abstract）

[24] 郑和祥，李和平，郭克贞，等. 河套灌区冬小麦冻结期土壤入渗特性分析[J]. 农业工程学报，2014，30（4）：70－78. Zheng Hexiang， Li Heping， Guo Kezhen， et al. Soil infiltration characteristics of winter wheat field during freezing in Hetao Irrigation District[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2014，30（4）: 70－78. （in Chinese with English abstract）

[25] 时立文. SPSS 19.0 统计分析从入门到精通[M]. 北京：清华大学出版社，2012：167－202.

Yearly variation of soil infiltration parameters in irrigated field based on WinSRFR4.1

Cai Huanjie, Xu Jiatun, Wang Jian, Chen Xinming, Zhu Dajiong, Xie Fei
（1. Key Lɑborɑtory of Agriculturɑl Soil ɑnd Wɑter Engineering of Northwest A＆F University, Yɑngling 712100， Chinɑ;
2. Institute of Wɑter-sɑving Agriculture in Arid Areɑs of Chinɑ， Northwest A＆F University， Yɑngling 712100， Chinɑ;
3. College of Wɑter Resources ɑnd Architecturɑl Engineering, Northwest A＆F University, Yɑngling 712100, Chinɑ）

Abstract:Soil infiltration parameters， which contain infiltration coefficient and infiltration index， determine the conversion velocity and distribution from irrigation water to soil water. Thus， they affect the irrigation effect and quality of ground irrigation and are of characteristic of time variations in summer maize-winter wheat rotation system， which may lead to different irrigation quality in different irrigation times. In order to reveal changes of soil infiltration parameters with time， this study obtained a series of infiltration coefficients and infiltration indexes of soil Kostiakov infiltration equation in different irrigation times based on field experimental data. The border irrigation experiment was conducted in 2012-2015 under summer maize-winter wheat rotation system at the Jinghui Canal irrigation area of Guanzhong Plain in Shaanxi Province. WinSRFR4.1，an integrated software for analyzing surface irrigation system， was used to estimate a field-averaged infiltration function from the field measured geometry in order to optimize the soil Kostiakov infiltration parameters. Manning function was to estimate the field synthetic roughness coefficient in different irrigation times， and then the Merriam-Keller post-irrigation volume balance analysis of WinSRFR4.1 model based on the advance-recession data was applied to simulate the process of field irrigation. Goodness of fit between simulated and measured values was evaluated by the root-mean-square error （RMSE） of advance-recession time and determination coefficient R2. The results showed that the root mean square error of the simulated water flow and the water flow regression processes were between 0.15-2.1 and 2.5-7.8 min， respectively. The coefficients of determination were more than 0.7. There were a wide variety of factors affecting soil infiltration parameters， such as soil bulk density， soil water content， organic matter， soil texture. Soil surface bulk density and water content changed with tillage，irrigation， and raining， which would affect soil infiltration parameters. Based on that， we took the soil surface bulk density， and soil water content as the main factors. According to the dominant factors affecting soil infiltration with the optimal soil infiltration parameters values， we had established the quantitative relationships between the infiltration parameters of Kostiakov infiltration equations and main factors， analyzed the yearly variations of soil infiltration parameters. The results indicated that the soil infiltration parameters changed significantly in the different irrigation periods with 95.0-210.0 mm/h and 0.42-0.67， respectively. And the relationship among the two infiltration parameters and soil moisture content， and soil surface bulk density conformed to logarithm function law， which adjusted R2was 0.846 and 0.741， respectively. According to these， we had built up the experimental regression equations to estimate the soil infiltration parameters of different irrigation period with soil surface bulk density and water content. These results have theoretical value for ascertaining irrigation technique parameters and have practical value for water management with irrigation.

Keywords:infiltration; models; soil moisture; summer maize-winter wheat rotation system; synthetic roughness coefficient

作者简介：蔡焕杰，男，河北藁城人，教授，博士生导师，主要从事农业节水与水资源高效利用研究。杨凌西北农林科技大学旱区节水农业研究院/旱区农业水土工程教育部重点实验室，712100。Email：caihj@nwsuaf.edu.cn

基金项目：国家科技支撑计划课题（2011BAD29B01）；高等学校学科创新引智计划项目（B12007）

收稿日期：2015-09-20

修订日期：2015-12-10

中图分类号：S152.7＋2

文献标志码：A

文章编号：1002-6819（2016）-02-0092-07

doi：10.11975/j.issn.1002-6819.2016.02.014