科学解释中的概率探析

■闫坤如



科学解释中的概率探析

■闫坤如

［摘要］科学解释与解释项和被解释项之间的概率关系密切相关，但是对概率的理解影响科学解释的发展，到底科学解释中概率是客观概率、倾向概率还是主观概率？这涉及对科学解释内在机制的界定以及对科学解释的研究。文章通过对客观概率及其解释困境、主观概率与科学解释、概率解释的恰当性条件等三个方面的论述，认为科学解释中的概率必须关涉解释主体的信念，也就是说，在解释的语境相关进路中的关涉解释者的信念才能避免解释陷入困境。

［关键词］科学解释；客观概率；主观概率

亨普尔在提出科学解释（scientific explanation）的演绎-律则模型（Deductive－Nomological Model）（1948）之后不久，于1965年提出了科学解释的归纳-统计模型（Inductive－Statistical Model），自此，概率进入科学解释的范畴，萨尔蒙（W.C.Salmon）的统计相关模型（The Statistical-Relevance Model）（1970、1971）和费茨尔（J.Fetzer）的因果相关模型（The Causal－Relevance Model）（1993）也诉诸对概率的理解上，雷尔顿（P.Railton)提出的概率解释的演绎-律则模型（Deductive-Nomological Model of Probabilistic Explanation）（1978）、汉弗莱（P.Humphreys）的科学解释的或然性模型（the Aleatory Model of Scientific explanation）（1981）和范·弗拉森（Bas. C.Van Fraassen）（1980）也关注解释中的概率，区别在于不同科学哲学家对科学解释中的概率的界定不同。但这些科学哲学家有一点是相同的，他们一般把概率作为客观世界的随机现象的数量统计或者解释主体的解释倾向，而不是作为主体的信念，这种对概率的理解导致解释陷入困境。想要摆脱解释困境，必须对概率做主观主义理解。

一、客观概率及其解释困境

根据对概率理解的不同，可把归纳逻辑分为三种：经验论归纳逻辑、逻辑主义归纳逻辑和主观贝叶斯主义归纳逻辑。经验论归纳逻辑和逻辑主义归纳逻辑立足于对归纳逻辑的客观理解，主观贝叶斯主义归纳逻辑为概率提供主观解释，把概率作为解释主体的信念度。

经验论归纳逻辑用统计频率解释概率，全称命题统计频率为1，是统计概率的特殊类型，即上述亨普尔的演绎-律则模型是归纳-统计模型的一个特例。经验主义归纳逻辑并未对全称命题中的主体信念随着证据增加而改变的情况加以说明。例如莱欣巴哈（Hans Reichenbach）、萨尔蒙认为概率是指某一性质或者事件在无穷序列中出现的相对频率的极限。莱欣巴哈提出概率只适用于无穷序列，而不解释单独事件，因此，在频率解释中，对不可重复的科学事实无法解释。

逻辑主义归纳逻辑以凯恩斯（J.M.Keynes）、卡尔纳普（R.Carnap）和欣迪卡（J. Hintikka）等人为代表，他们从逻辑主义的视角分析一个命题的确证度。例如，凯恩斯将概率视作命题间的一种二元逻辑关系，“令命题集合h为前提，命题集合a为结论，如果对h的知识使得我们能对a有程度为α的合理信念，那么，我们就说a和h之间有程度为α的概率关系”。［1］3凯恩斯把概率当成无限事件序列的性质，因此，无法指派个别事件的概率值。在逻辑主义归纳逻辑看来，单称命题的概率不可测度，那么，如何对科学中的单独事件进行解释呢？例如“明年发生世界大战的概率是多少？”这样的单独事件不管用频率概率还是逻辑概率都无法得到解释。不管是经验论的归纳逻辑还是逻辑主义的归纳逻辑都把概率做客观概率，概率是通过经验或者逻辑推导获得，概率关涉归纳主体。

经验论归纳逻辑概率的基础是无差别原则（principle of indifference）。所谓无差别原则指的是如果没有充分证据使得我们能够认为两个事件中的一个比另外一个具有更高概率的可能性，那么，我们必须赋予两个事件同等的概率值。即在一组互斥的可供选择的证据中，其证据在认识论上中立。“无差别原则宣称，如果没有已知的理由对我们所讨论的主题中的一个备选对象做出比其他备选对象更强的断言，那么，相对于这样的知识，关于每一个备选对象的断言都有着相等的概率。”［1］42学术界关于无差别原则的争议很大“这个原理的风险在于，将同种类的所有事件还原（reducing）成一定数量的相同可能事例。换言之，正如我们也许对这些事件的发生，以及确认支持所求事件概率的事例数量都同等的不确定。事例数量与所有可能事例数量的比例就是这个概率的测度，因此该概率是一个简单的分数，其分子是支持事例的数量，分母是所有可能事例的数量”。［2］无差别原则是给所有可能事件指派相同概率值。概率是无限事件序列的性质，但不能给个别事件指派概率值。例如，投掷一枚硬币，其国徽面朝上的概率值是什么？我们只要根据经验，不需要大量重复性实验，就知其概率是50%。这种概率需要经过经验分析才能得到，这种概率是先验概率（prior probability）。与此相反，后验概率（posterior probability）指的是从结果信息中修正的概率，例如对于某地男孩出生的概率需要多年观察和不断修正才知其概率，这种概率是后验概率。

还有一种概率的客观解释是倾向（propensity）解释。费茨尔等人坚持概率的倾向解释。倾向解释中的概率是一种给定情景下产生某种结果的物理趋势或倾向。费茨尔把概率看成机会结构（chance setups）的概率倾向。费茨尔认为萨尔蒙统计相关模型存在困境的根本原因在于萨尔蒙把概率理解为极限定律，但极限定律不能判断性质间具有律则性关系。“解释理论所面临的困难之一是建立概率定律和其显现（manifestation）之间的正确关系。概率可被看作是机会结构的概率倾向而不可看作是极限频率”。［3］概率的倾向解释中的倾向不是表征个人的主观倾向，而是表征机会结构或“实验安排”（experimental arrangements）的客观性质，倾向表达客观的因果力、客观机制和实验上的客观安排。例如，“糖放水里会融化”是一种客观的倾向，这是本体论意义上的叙述，语句言说了事实本身是这样。在这种意义上费茨尔的因果相关模型也是表达理论和事实之间的关系。

雷尔顿（P.Railton)在1978提出了一种解释的新模型——“概率解释的演绎-律则模型（Deductive -Nomological Model of Probabilistic Expalnation）”，简称为D-N-P解释模型。雷尔顿把世界看成一个有内在机制的机器从而提出了科学解释的模型，这个模型能够解释亨普尔模型不能解决的低概率事件。

D-N-P的解释模型［4］的逻辑表达式如下：

其中e表示被解释项，Ge，t0表示e在t0时刻具有G属性。

以原子U238自发的α衰变的量子力学解释为例说明雷尔顿的D-N-P解释模型。如果想解释U238衰变现象，首先要知道U238的半衰期，确定衰变规律和其他附加条件导出U的衰变概率才能解释U的衰变。（1）由一个基本理论（量子力学）来导出U238的衰变半周期为450亿年；（2）确定U238的单个原子在T时间里的衰变概率规律；（3）陈述被解释对象u的初始条件；（4）导出U的衰变概率；（5）说明u实际已经衰变了。

根据以上条件，U238衰变现象解释的D-N-P模型如下：

（1）从量子力学中导出（2）

D-N-P模型把解释的重点放在U衰变的概率而不是U是否衰变。至于衰变的概率和衰变的关系，既不是演绎相关也不是归纳相关的，因此亨普尔把解释看成论证是错误的。雷尔顿的D-N-P模型与亨普尔的归纳-统计模型是不同的，在亨普尔的解释模型中，只要知道U238的统计规律和线性条件就能知道是否能够解释U238衰变，这取决于解释中的概率值，根据亨普尔模型的高概率要求，如果统计规律是高概率的就能解释为什么U238衰变，如果概率是低概率就不能解释为什么U238衰变。雷尔顿的D-N-P模型因其注重对于事件的内在机制的阐明，因此即使是低概率事件也可以得到解释。

雷尔顿采用的是倾向概率，倾向是不确定性因果关系的趋势，倾向不可能从现在向过去运行，因此，雷尔顿的D-N-P模型用于解释单个事件的概率倾向是物理概率，而不是统计概率，这与亨普尔的概率解释不同。但雷尔顿的内在机制过于抽象，解释主体难以把握，例如，抛硬币国徽面朝上的有很多随机因素使得我们不能阐明其内在机制，那就不能解释这个事件，而运用亨普尔的归纳-统计模型就能够解释。雷尔顿陷入解释困境的原因在于他把解释看成是客观的，排斥主体信念，他立足于客观概率的基础上，没有考虑主观概率，因此导致其模型遇到了困境。

唐纳德·吉利斯以是否关涉人类的信念为根据把概率分为两种：一种是客观概率，另一种是认识论概率。客观概率把概率看作客观世界的特征，概率与人类的知识或信念无关。亨普尔的归纳-统计相关模型以及萨尔蒙的统计相关模型都把概率看作频率解释，他们把概率看作是一个序列的相对频率的极限，而费茨尔和汉弗莱的倾向解释把概率看作一种物理倾向，这些类型的概率采取的都是客观概率解释。这些模型遇到了困境原因就在于他们对概率不涉及人类信念，“无论莱欣巴赫的频率解释，还是卡尔纳普的逻辑解释，都没有超出帕斯卡型概率的范畴。事实证明，这种归纳逻辑在科学研究的实际应用中遇到了种种困难，造成这种困难的根本原因是因为这种归纳逻辑没有恰当地反映知识增长的局面。越来越多的现代逻辑学家也认识到了这一点。要解决这些困难，有两种不同对策。一是保守的策略：让科学实际迁就逻辑句法，至多是调整辅助假说，以维护旧逻辑的核心原理。二是激进的、革新的策略：采用新的逻辑句法以适应科学实际。换句话说，后一种策略认为问题的症结恰恰在于经典概率演算的核心原理需要修改。”［5］

与客观概率解释不同，认识论概率把概率看作个人或群体拥有的知识程度、信念度或合理信念度。据此界定，主观主义的概率解释是认识论意义上的概率解释。客观概率解释因为不能解释单个事件以及无差别原则的导致遭遇解释困境，因此，在概率解释中必须涉及到主体信念。

二、主观概率与科学解释

主体信念在概率中不可或缺。主观概率是个体或者群体的信念度，是人们对于某命题的合理性相信程度，它表示支持证据不同的解释主体对同一个被解释项赋予不同概率值。主观概率的代表人物是拉姆赛（F.P.Ramsey）、德·菲尼蒂（B.de Finetti）、萨维奇（L.J.Savage）和杰弗里（R.Jeffrey）等人。他们把概率界定为主体信念度。

在科研和生活中，存在很多不能大量重复的随机性事件，这些事件未必能够通过实验或经验得到概率值，而只能通过解释主体的主观信念来确定各种可能性结果的概率值。像对“明天是否下雨”这样的自然现象的解释，经验主义的频率解释以及逻辑主义派的逻辑概率都不能达到解释的目的。因此，科学解释必须涉及到解释主体的信念，在解释中必须引入主观概率，或者说，必须对解释中的概率做主观概率方面的认识。解释主体根据经验或者天气预报，相信明天下雨的概率是80%，这才能对“明天是否下雨”的合理性进行分析。这种不能重复的随机性事件可以用贝叶斯定理来刻画。假定随机事件A和B，对其概率进行刻画的贝叶斯定理可以表示为：

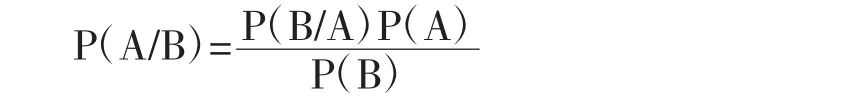
在上式中，P（A|B）是在B发生的情况下A发生的可能性。P（A）是A的先验概率。之所以称为“先验概率”，因为它的概率值不依赖于B的概率值。P（A|B）是B发生后A的条件概率，A的概率值取自B的值，因此，其为A的后验概率。P（B| A）是A发生后B的条件概率，B的概率值取自A的值，因此，其为B的后验概率。P（B）为B的先验概率。

主观贝叶斯主义强调贝叶斯定理在主观主义概率演算中起关键作用。主观贝叶斯主义允许不同解释主体对同一个假说赋予不同的概率值，同时允许解释主体根据新信息修正信念从而调整后验概率。先验概率是指解释主体根据背景知识或主观判断所相信的某事件发生的概率，该类概率没有经受检验，又称为验前概率。先验概率分为客观先验概率和主观先验概率。客观先验概率指的是利用背景知识得到的概率；主观先验概率指的是没有背景知识或在背景知识不完全的情况下，仅仅凭借解释主体的主观经验判断得到的概率。

主观概率立足于解释主体的个人信念，解释主体对于概率的确定，没有必要遵守特定规则，主观主义的概率可以把概率定义为在给定证据e时，对假说或者理论的主观信念度。主观概率以解释主体的主体信念为基础，根据已有经验和证据对概率进行调整。

例如：某地居民的肺癌发病率为0.0004，现用新检测法发现之前的化验结果是错误的。已知患有肺癌的人其化验结果99%呈阳性(患病)，而没患肺癌的人其化验结果99.9%呈阴性(没有患病)。试问：在化验结果呈阳性的人中可患有肺癌的概率是多少呢?

如果我们用A表示“化验结果呈阳性”，用H表示假说“被检查者患有肺癌”，那么根据上述表示可知：

P（H）（该地居民的肺癌发病概率）=0.0004

P（┐H）（该地居民没患肺癌的概率）=1-0.0004=0.9996

P（E/H）（患肺癌者其化验结果呈阳性的概率）=0.99

P（E/┐H）（没患肺癌者其化验结果呈阳性的概率）=1-0.999=0.001

欲知P（H/E）的值，即在化验结果呈阳性的条件下“被检查者患有肺癌”的概率，可以根据贝叶斯定理得到。

P（H/E）

=P（H）P（E/H）/P（H）P（E/H）+P（┐H）P（E/┐H）

=0.0004×0.99/（（0.0004×0.99）+（0.9996×0.001））

=0.284

这表明在化验结果呈阳性的人中“患肺癌”的人的概率是28.4%。这与“某地居民的肺癌发病率为0.0004”数据有差异。解释主体会根据新的信息对患病概率进行调整，修正先验概率，从而对新的实验结果进行解释。

从上例我们可以看出，解释主体就是借助新的实验结果或者新证据来修正先验概率，进而改变解释主体的信念度。概率的主观主义解释表明，概率只是解释主体头脑中所具有的信念证据。主观概率解释中的概率描述的是主观信念的程度，而不是客观频率或者概率倾向。

假说h的先验概率，就是在不检验证据e的情况下，假说h可能为真的概率。假说的先验概率的并不取决于概率演算系统，而取决于解释主体的背景知识和信念。主观主义概率针对单个事件或者不确定性事件，主观概率表现为对仅发生了一次的事件或对未知状态的主观估计，像“张三这次买彩票中大奖的概率是多少”这样的单个事件如何解释？经验主义概率和逻辑主义的概率都不能解释，但主观主义概率能够解释这个单个事件。

三、概率解释的恰当性条件

根据贝叶斯定理，解释主体对于同一个命题、事件或假说的合理的信念度集合并不唯一，只要解释主体的信念是遵循概率论的公理，那么就具有合理性。解释主体具有差异性，但如何解释群体信念的一致性或者说如何避免主观概率的随意性呢？作为主观贝叶斯主义发展的德·菲尼蒂的“意见收敛定理（convergence theorem for opinions）”［6］和吉利斯（D. Gillies）的主体交互概率（intersubjective probability）对避免主观概率的随意性做了辩护。

德·菲尼蒂的意见收敛定理的致力于解决“主体间性”问题，不同解释主体通过吸收新知识，按照贝叶斯定理对新证据加以吸收，从而修正先验概率，逐步取得一致的后验概率。随着解释主体对证据的吸收，先验概率的主观任意性被后验概率的客观确定性所取代，从而避免了主观随意性。意见收敛定理可以解释个体或群体合理信念度的一致性。概率的主观随意性在长序列中趋于确定性的稳定值，意见收敛定理避免了主观概率的随意性。

吉利斯提出主体交互概率来避免解释主体的信念的随意性。“这种主体交互观点是主观主义理论的发展，在这里，概率不是看作一个人的信念度，而是一个社会团体的一致信念度。”［7］2个体的概率具有群体趋同性的趋势，不同群体的信念度也会趋向一致性。不同群体“确立沟通与信息交流机制从而讨论形成共同意见（consensus），或者说主体交互概率”［7］174。吉利斯不但定义了主体交互概率，同时还给出了恰当性条件。吉利斯认为，主观概率解释中涉及到的信念不是个体的信念，而是社会群体的共同信念，个体可以通过与群体交互作用，沟通信息和证据从而获得一致的信念。并且，不同群体的信念度也可以通过相同过程取得一致信念。群体信念度的趋同性两个必要条件：第一，解释主体具有共同的旨趣，解释主体都立足于解释同一个命题或者事件，解释主体必须被共同的目标所维系。第二，共同体成员间保持信息沟通。共同体的成员之间通过交流达到信念一致。吉利斯的主体间信念度是一个条件信念度。解释主体对解释项

e分派概率为p(h)，这是条件概率p（e/k）的简化形式，其中k是组成解释主体知识、信念集合。主体间信念度逻辑形式也是p（h/k），这里的k是科学共同体的知识背景，一般来讲，科学共同体的知识背景真包含共同体的任何一个成员所拥有的知识背景。解释主体与具有共同旨趣的科学共同体通过信息交流形成的“公共知识”，这样就形成了群体的一致信念度。由于信念度的主体间性特征，在相同的知识背景和实验证据下，解释主体的先验概率会被科学共同体合理的一致性验后概率来代替。例如，不同解释主体对于“时空”具有不同的信念，爱因斯坦坚持“绝对时空观”，而牛顿坚持“相对时空观”的信念，这表现为解释主体主观概率的差异性。但不能把其界定为解释主体个人的信念度，按照吉利斯的理解，牛顿和爱因斯坦的时空观信念也是科学共同体的时空观信念，而非牛顿和爱因斯坦的个人时空观信念，即使在开始是由牛顿和爱因斯坦提出和坚持的。根据吉利斯的观点，两种关于宇宙的信念通过解释主体间的沟通会最终趋于一致，会随着证据的增加修正信念，使得群体的信念保持一致。例如，在笛卡尔看来，宇宙是一口大钟，运动是由物体之间的接触、碰撞而引起的，这与亚里士多德对宇宙的信念不同。亚里士多德的宇宙信念是上帝创造万物，地球是宇宙的中心，其他星体围绕地球运转，宇宙有边界。笛卡尔宇宙观取代亚里士多德宇宙观，或者现在科学家坚持一个共同的宇宙观，这表明了主体信念的一致性。同时，解释主体可以在不同的范围坚持不同的信念，例如，在宏观世界坚持牛顿的相对时空信念，在微观世界坚持爱因斯坦的绝对时空信念。吉利斯通过这两个条件保证了主观概率解释进路的恰当性，从而避免了主体信念的随意性。

吉利斯主体交互概率理论给出的避免主观概率随意性的条件能否解决主观概率的大部分诘难，但有人指出给出的信念主体间性的条件过于简单和武断。例如，凯伯格（H.E.Kyburg）就指出“（贝叶斯主义）原理并没有表明，一个人应该变化他的信念来与贝叶斯定理保持一致”［8］关于主体概率如何才能满足解释的恰当性条件还值得深入探讨，但对解释中的主体信念的理解相对于不关涉解释主体的模型能够推动对科学解释的研究。

参考文献：

［1］Keynes J M. A treatise on Probability［M］. London: Macmillan an Co.ltd，1921.

［2］Laplace P S. Essai Philosophique sur les Probabilies，Page references are to Philosophical Essay on Probabilities［M］.New York: Dover Publications，1951:6-7.

［3］J H Fetzer. Philosophy of Science[M]. New York: Paragon House, 1993：71.

［4］Railton P. A Deductive-Nomological Model of Probabilistic Explanation［J］.Philosophy of Science，1978，45（2）：206-226.

［5］任晓明，桂起权．非经典逻辑系统发生学研究［M］．天津：南开大学出版社，2011：116-117.

［6］B D Finetti. Foresight: Its Logical Laws, its Subjective Sources［C］//Studies in Subjective Probability，in H. Kyburg and H. Smokler（eds.），New York: John Wiley，1964：93-158.

［7］Donald Gillies. PhilosophicalTheories of Probability［M］.New York: Routledge，2000.

［8］H.E.Kyburg. Epistemology and Inference ［M］. Minneapolis:Unversity of Minnesota，1983:95.

［责任编辑：李君安］

Study on Probability of Scientific Explanation

Yan Kunru

Abstract：Scientific explanation is closely related to probabilistic explanation with relations between explanadum and explanans, and the understanding of probability influences the development of scientific explanation. What is the probability in scientific explanation? Is it the objective probability or the subjective probability? This involves with the defining of inherent mechanism of scientific explanation and the study of scientific explanation. The probability in scientific explanation is related to the beliefs of interpretive subject.

Key Words：Scientific Explanation；Objective Probability；Subjective Probability

［作者简介］闫坤如，华南理工大学马克思主义学院教授、哲学博士（广东广州，510640）。

［收稿日期］2015-11-22

［中图分类号］N02

［文献标识码］A

［文章编号］1673-8616（2016）01-0064-07