接触网腕臂结构系统防松研究
韩凌青,李少鹏,张慧洁
接触网腕臂结构系统防松研究
韩凌青,李少鹏,张慧洁
根据实际工况建立了腕臂结构系统的有限元模型。利用有限元法对该模型进行受力分析,校核其静强度、静刚度。建立了腕臂结构系统的动力学模型,通过模态分析得出模型的前十阶固有频率及振型,并通过谐响应分析计算在外载荷的影响下结构的共振频率。通过对腕臂结构系统的动力学分析,得出在外载荷作用下,整体结构系统不会发生共振现象,与实际工程项目相符。同时分析出腕臂结构的连接件中振动影响最大的部件,为螺栓防松提出建设性意见,并为工程实际提供了理论支持。
有限元法;固有频率;防松;动力学分析;腕臂结构
0 引言
在接触网设计施工阶段应尽量避免发生共振现象,以防止降低其结构的可靠性、螺栓螺母的松动以及影响受电弓的受流特性[1]。高速列车受电弓在经过定位线夹的时候,会对腕臂结构系统造成冲击及振动,同时风载荷、接触线张力等外载荷的变化对接触网整个结构系统也会产生一定的影响。对接触网系统,正常行车的情况下,接触线垂直方向固有频率在1 Hz左右[2]。目前鲜有腕臂支撑结构以及其与接触线之间的共振关系进行分析计算的研究,一般只依靠工作经验,没有理论支撑。国标中对此没有严格要求,该项往往被忽略,淡漠了结构的动态性能。同时,螺栓螺母的防松措施种类繁多:机械防松、破坏性防松、摩擦防松。经济性和适用性也各不相同。腕臂结构系统的防松措施比较陈旧,现场反馈的问题也较多,亟待对该类问题结合经济实用性进行优化解决。
本文通过对腕臂结构系统进行模态分析、谐响应分析以及相关力学计算,对整体结构系统的动力学性能进行分析评估,验证模型与实际工况的符合程度,并提出相应的优化方案。
1 结构静力学模型及特性分析
本文选用最不利工况,即下锚支的大限界腕臂结构系统作为分析对象。腕臂底座间距1.8 m,平腕臂总长4.1 m,且为钢腕臂结构。建立完整的SolidWorks实体模型,并对模型根据实际工况进行简化,完成有限元模型的转化。同时,有限元模型的腕臂和绝缘子用空间梁单元模拟,腕臂支撑用杆单元模拟[3,4]。图1 a为该腕臂结构系统的SolidWorks实体模型,图1 b为其Ansys的有限元简化模型。
实际工作状态中,考虑到接触线的张力、自重、风载荷、冰雪载荷以及下锚等引起的额外负载,对腕臂结构系统进行静力分析[5]。
本文由于旨在分析腕臂结构的整体受力情况,为了排除所有由于建模原因可能引起的局部应力使计算结果更符合工程实际,对结构衔接处的连接件(螺栓、定位环等)进行简化,以两点耦合的形式模拟铰接。同时由于绝缘子结构在建模时极易引起局部应力,且其对计算结果影响极小,故将其简化为简单的圆柱体结构,但其质量、尺寸与真实情况相符。
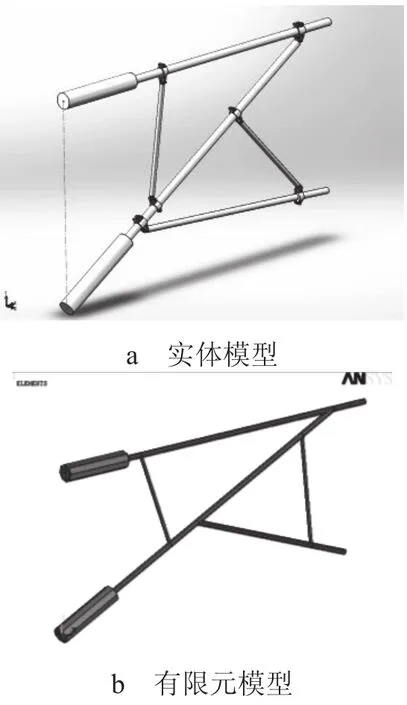
图1 腕臂结构系统模型图
采用基于铁木辛柯梁理论[6][7]的BEAM188梁单元进行模拟。本文的腕臂结构系统模型可简化为空间弹性支撑连续梁,根据相关文献,可导出连续梁单元有限元方程[8]:
节点位移函数为

式中,vi为单元节点i处的位移;θi为单元节点i处的转角;vj为单元节点j处的位移;θj为单元节点j处的转角;l为i、j节点间的距离。
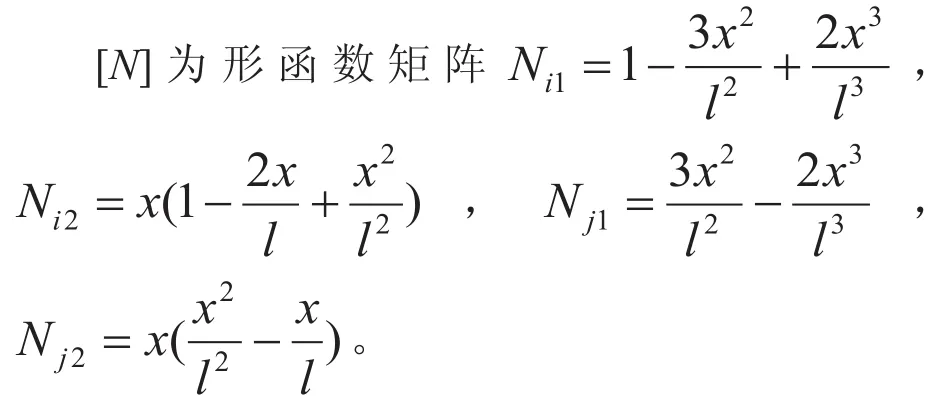
用节点位移表示的单元应力的关系为
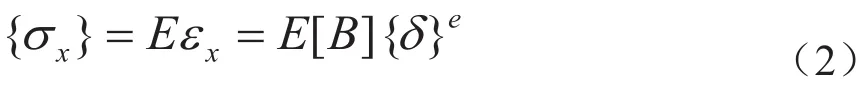
式中,E为材料的弹性模量。
用节点位移表示单元的刚度矩阵为
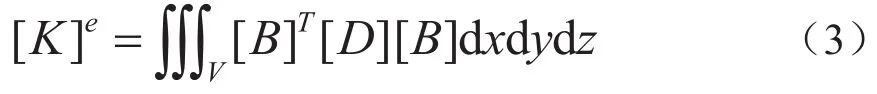
考虑到[D]为与材料弹性模量有关的矩阵,且横截面惯性矩,由虚功原理建立作用于单元上的节点力和节点位移之间的关系式,即单元刚度方程为

式中,{F}e为单元节点力分量列阵,由此可解出[K]e。
综上所述,利用有限元法进行计算时的方程可描述为

式中,[K]为结构的总体刚度矩阵,由各单元的刚度矩阵组成;{δ}为节点位移列阵;{F}为节点载荷列阵。
通过将实际的位移边界条件带入式(5),解之可得单元的节点位移,再通过单元特性分析建立的关系式,即可求得所需应力、应变。
本文通过Ansys有限元计算软件对模型进行强度、静刚度分析计算,结果如图2和图3所示。

图2 腕臂结构系统最大应力图

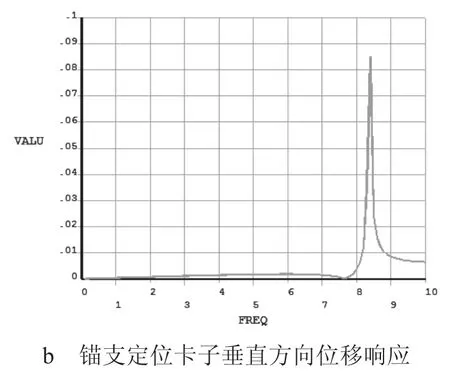
图4 腕臂结构谐响应分析图
同时,本文截取定位环、套管双耳、支撑管卡子等连接件进行局部谐响应分析,找出受振动影响最大的部件,结果如图5所示。可见受振动影响强弱的排序为定位环、支撑管卡子以及套管双耳。施工人员可根据受影响的严重程度对相应螺栓螺母进行择优选取,用不同等级的防松件来应对不同的振动情况。
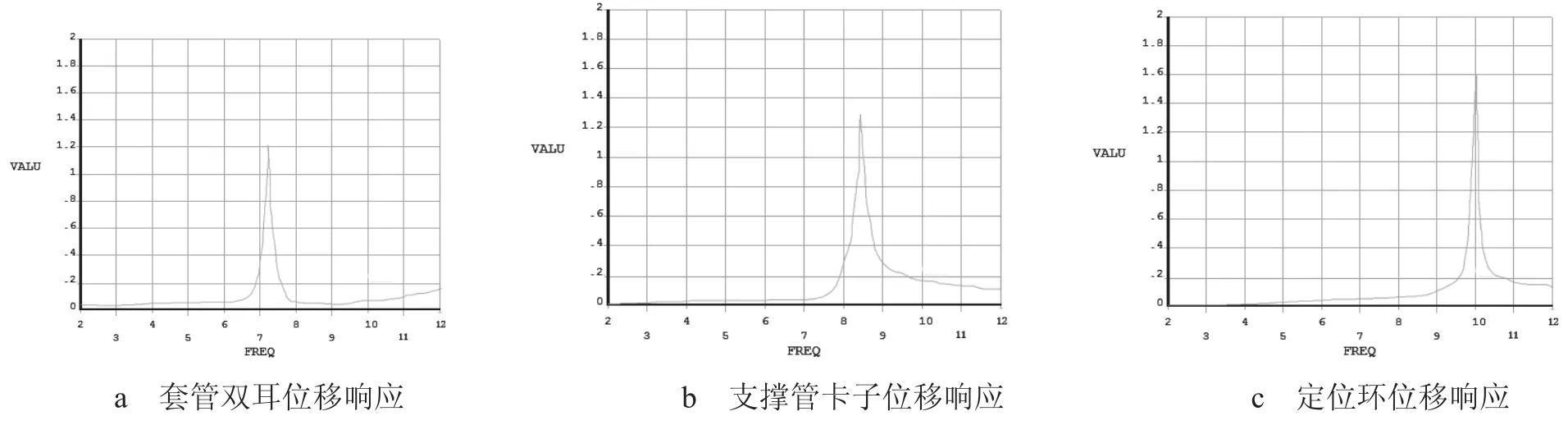
图5 谐响应分析曲线图
3 结论
本文根据工程实际,建立了腕臂结构系统的实体模型和有限元模型。通过对模型的分析计算,校核了结构系统的静强度、静刚度,并对外载荷作用下的结构系统进行了动力学分析。通过模态分析以及谐响应分析确定了结构的固有频率。由以上计算可得,本文所建立模型的静强度、静刚度满足使用要求,并且在外载荷(接触线张力、受电弓、风载荷等)作用下不会发生影响整体可靠性的共振现象,与实际情况相符,为实际工程项目提供了理论支持。同时,通过本文的计算,得出结构振动的基本形式,分析并概括了各连接部件的振动情况,为施工单位防松螺栓螺母的选取提供了一定的理论支持。对螺栓螺母的防松研究有一定的指导意义。
[1] 林裕华. 高速铁路接触网零部件的重要度分析[J]. 电气化铁道,2011,22(2):9-11.
[2] 刘长利. 高速铁路接触网低频振动及零部件防松技术分析[J]. 铁道标准设计,2014,(10):113-116.
[3] 于兰峰,王金诺. 塔式起重机结构系统动态优化设计[J].西南交通大学学报,2007,42(2):206-210.
[4] 刘峰涛. 接触网腕臂支持结构的仿真分析[J]. 电气化铁道,2004,(6):19-25.
[5] 李保华. 基于有限元的腕臂结构静动态特性研究[D].西南交通大学,2009.
[6] 蒋纯志,金桂,陈亚琦. 等截面铁木辛柯梁的分布传递函数方法[J]. 湖南科技学院学报,2009,30(8):50-53.
[7] 金晶,邢誉峰. 铁木辛柯梁固有振动频率的边界元解法[J]. 北京航空航天大学学报,2012,38(7):976.
[8] 成思源. 有限元法的方法论[J]. 重庆大学学报:社会科学版,2001,7(4):61-63.
[9] 常国安,彭昶. 京沪线电气化工程接触网腕臂计算分析[J]. 电气化铁道,2006,(2):26-28.
[10] Weihua Z. Dynamic studies on catenary[J]. Journal of The China Railway Society, 1991.
[11] 许佳. 梁结构振动响应的小波有限元法实现及应用研究[D]. 苏州大学,2012.
[12] 宋伟. 弓网系统动力学分析[J]. 电气化铁道,2012,23(2):24-27.
A finite element model of cantilever structure was set up based on the engineering practices. The loading analysis was performed by using finite element method to verify the model’s strength and stiffness. The kinetic model was established for the cantilever structure system, the first ten inherent frequencies and modes of resonance were obtained through the modal analysis, and the calculation of resonance frequency of the structure under the external load were performed on the basis of the harmonic response analysis. A conclusion was obtained that the resonance frequency will not occur on the entire structure system under the action of the external load, and it is identical to the actual engineering actuality. The most impacted connecting parts in the cantilever structure caused by the resonance were identified at the same time after the analysis. The constructive proposals for locking of bolts were raised, and the theoretical supports for the engineering practices were provided.
Finite element method; inherent frequency; looseness proofing; kinetic analysis; cantilever structure
U225.4+2
:B
:1007-936X(2016)01-0024-04
2015-06-30
韩凌青.铁道第三勘察设计院集团有限公司,工程师,电话:13752393334;李少鹏.铁道第三勘察设计院集团有限公司,助理工程师;张慧洁.天津市赛英工程建设咨询管理有限公司,助理工程师。

