填铺“复习题与测试题”间的鸿沟——以“表面积和体积”为例谈补充练习的有效设计

浙江杭州市萧山区新街第三小学（311200）陈霞英



填铺“复习题与测试题”间的鸿沟——以“表面积和体积”为例谈补充练习的有效设计

浙江杭州市萧山区新街第三小学（311200）陈霞英

［摘要］小学高段数学课堂教学中，学生在学习求表面积和体积内容时，在复习题与测试题中间往往存在着知识点的断层，不能对知识进行有效迁移。根据学生的认识特点，通过借助实物、动态演示、有效补充练习等方法，让学生在学习表面积和体积知识点时，掌握一定的数学思考方法，融会贯通，弥补知识断层，提高学习的有效性。

［关键词］面积计算补充练习有效性

在复习求表面积和体积的内容时，百分之七十左右的学生做训练时思路通畅，解题正确率接近95%~ 100%，但是遇到单元、期中、期末测试中的几何综合应用部分的题目时却目瞪口呆、无从下手……一道表面积的综合应用题，全班的正确率竟然为0%！与学生交流时，他们表示：“测试时我老是在脑子中找与它相同的复习过的题目。在考试时我的手会发抖，心会发慌……”这都说明了测试题的“情景”在变，学生的“情绪”就会紧张，也就是学生在复习题与测试题中间有一条“情景”和“心理”鸿沟无法跨越。为改进常规的复习方法，我在几何复习课后期设计了“补充练习”，让学生通过“补充练习”来填铺鸿沟。

一、借助具体物品，静心看、想、叠、折，自悟缺陷

1．看清楚后计算

课始出示规范的、完整的实物（牙膏壳、魔方等），借助学生的生活经验与直觉感受，请每个学生都举出至少10个实例。

生1：教室、课桌、房子、书本……

生2：正方体的小蛋糕、抽屉、烟囱……

师：生2的“抽屉、烟囱”这2个例子较典型。你们知道老师说的“典型”的含义吗？

生3：抽屉少一个上面，烟囱上、下底面都没有。“典型”在于“5个面”和“4个面”。

为使学生都明白“典型”在哪里，我还拿出了实际的抽屉和烟囱的模型让学生观察。在“典型”题的面前，学生不由得惊叹：“啊！我真粗心。上次我把抽屉、烟囱都算成6个面了……”

2．想明白再列式

在补充练习中，我设计了不规则立方体的表面积计算方法。如图1，在一个完整的立方体中取走一些小立方体，形成一个不规则立体图形。

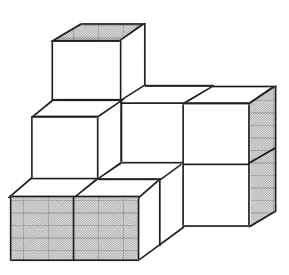
图1

①这样的图形也可以用六个方向的面来研究吗？

②相对的两个面的面积一定相等吗？

面对这种类型的题目，很多学生望而生畏，但只要提示学生从“六视图”的角度出发，问题就能迎刃而解。

3．叠“几”层比方法

方法比较：尝试用不同的角度和方法研究立体图形的表面积。

读者会将在服务过程中获得的利益、服务过程的感受、读者对阅读推广服务的情感依赖关系等浓缩在对品牌的认知中，即品牌是读者对服务的全部体验。所以，实质上品牌是属于读者的，一旦失去了读者，也就失去了品牌，所以好的服务体验以及对服务的价值认同才能促成品牌的形成。

图2中的三个立方体的棱长分别是4分米、2分米、1分米。问：这个模型的表面积是多少平方分米？（小组讨论）

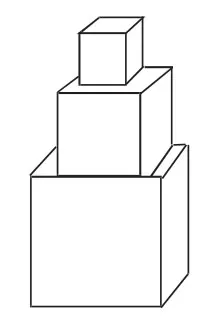
图2

A组：把三个立方体的表面积都求出来，然后减掉重叠的部分。

B组：单独算出四个侧面再加上两个底面。

C组：只要算出最大立方体的六个面，然后加上其他两个立方体的侧面和。

……

学生在各小组的汇报中自悟，最终找到适合自己的正确方法。

4．拆“大楼”、堆“柱子”

为激活学生的思维，在复习课中，我让学生把一个长方体看做是一幢“大楼”或一些正方形砖堆。

图3－1

图3－2

图3－3

学生通过动手操作，明白“堆积”的“柱子”和“大楼”的个体元素不变（体积不变）但表面积是完全不同的。在动态堆积中学生潜心学习、认真作答，此题竟然无一人出错，真是令人欣喜。

二、依据动态变换，潜心切、浸、挖、铺，自填鸿沟

大多数学生对“表面积和体积”的计算都存在情绪上的抵触，空间观念淡薄，想象能力缺乏。为改进教法，我在复习伊始对点、线、面、体四个主要元素进行动态演示。

最原始的元素为：

用课件在屏幕上动态演示后，我再根据教室处于教学楼三楼的情况，提出：“今天我们在长方体里面上课，大家同意吗？我们的房间一般都是长方体，我们在长方体里睡觉、学习、吃饭……大家看教室顶面与黑板墙角相交的线，找到了吗？教室长方体的三个面的交线的交点找到了吗……”每一个学生的眼神都告诉我，动态演示效果非常好。紧接着我就用以下切、浸、挖、铺四个题目让每个学生进行练习。

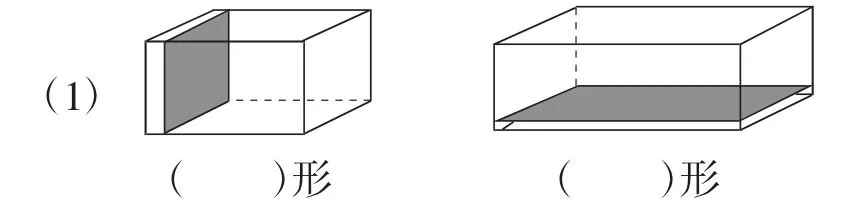
（2）如图4所示，往边长为10厘米的立方体水箱注水至5厘米深，然后把长为4厘米、宽为3厘米、高为5厘米的长方体铁块放进水中，水深变为多少厘米？

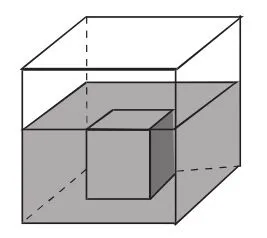
图4

图5

（3）如图5所示，从棱长是5厘米的立方体木块上挖掉一个棱长是1厘米的小立方体，求剩余部分的体积和表面积。

（4）学校要用沙填铺一个长为4．5米、宽为3米、深为0．5米的长方体坑，每立方米沙重1．7吨。需要多少吨沙才能填满这个坑？

通过以上切、浸、挖、铺的训练，学生都牢牢掌握了长方体的表面积计算方法。我欣喜地看到，每个学生对复习题的题旨有了深切的理解，对测试也消除了“畏难”情绪。

三、凭借“有效补充”，悉心指导铺平鸿沟

复习后进行了一次测试，实践证明复习方法十分有效。以下是两个单元测试题中的一些综合题：

（1）求阴影部分的面积。

（2）求截面的面积。

第（1）题的正确率达85%；第（2）题在以往只有50%的学生得出一种答案，而经过复习后，三题都能做对的学生占80%，说明学生“切、折、做”的能力在不断提升。

四、践行感悟

规则的立体图形如长方体与立方体，其表面的计算是容易的，因为有一个现成的计算公式，学生掌握了这个公式之后，剩下的就只是代入公式计算了。这种知识掌握得再扎实，技能训练得再熟练，仍然只是知识与技能，还上升不到数学思想与方法的层面。对不规则图形表面积的研究，显然要比规则的图形复杂得多。面对千变万化的不规则图形，我们有没有一种方法能够把握它呢？这就是一个重要的数学思考。显然，通过对应，可以把不规则的图形转化为规则的图形进行研究。数学中对应的思想在这里发挥了重要的作用。

规则的立体图形，相对的面相等是显而易见的。而不规则的立体图形，相对面的面积是否相等，这需要理性的思考，而理性思考的支柱就是对应的方法。教学中通过提问：“这样的立体图形（不规则的立体图形）也可以通过6个方向的面来研究吗？相对的两个面的面积一定相等吗？”引发学生的认知冲突：原有的知识与经验是否能应用在新问题的解决之中？以这两个问题作为思考的起点，进一步设计丰富多彩的教学活动，让学生在这些活动中通过不同的研究方法，聚焦到同一个研究结论，即“相对面的面积相等”。其中，有两个特别关键的步骤。首先，学生通过列表计算，归纳出相对面的面积相等；进而，通过师生之间的讨论，配合动态演示，揭示相对面之间的关系。对应的方法在学生充分的思考与交流中慢慢“浮出了水面”。可以说，学生获得这个思路的过程，充满了“艰辛与曲折”的思考，而正是这样的艰辛与曲折，体现了教是为了不教的目的，也正是经过这样的艰辛与曲折，学生才能体会到数学思考的独特魅力。

（责编金铃）

［中图分类号］G623.5

［文献标识码］A

［文章编号］1007-9068（2016）01-074