重温 重组 重塑 重开——例析“圆柱与圆锥整理和复习”教学的“四重”环节
浙江杭州市萧山区新街第四小学(311200)马金锋
重温重组重塑重开——例析“圆柱与圆锥整理和复习”教学的“四重”环节
浙江杭州市萧山区新街第四小学(311200)马金锋
[摘要]复习课难上,传统的复习教学模式确实使教师、学生容易产生倦怠情绪。为改变传统的复习教学模式,教师可设计“四重”环节,即重温、重组、重塑、重开,把以机械做题训练为主的复习过程变换为有多重想象、多样思维、互相呼应的互动场景,让学生在动手操作中细心解题、领悟复习内容,其效果较明显、实在。
[关键词]数学教学教学模式复习四重潜心
在农村小学,尚有不少的常态数学复习课依然存在着内容单一、训练单调等现象。“究竟如何使数学复习课教学有新意”“怎样才能让数学复习课教学更有效呢”,这是我们一线数学教师普遍关注的课题和话题。为改变传统的“整理内容→系统复习→针对训练→布置作业”的复习课教学模式,我从2011年秋季开始,采用了“四重”环节复习教学模式。可以说,践行的复习课教学新模式充分体现了复习是师生双边活动的展示过程,是各层次学生对知识技能掌握程度的暴露过程,更是激励每个学生重开数学智慧大门的逻辑起点。
一、重温基础知识,激发学生动手操作
为改变传统的数学复习课让学生自主复习或背诵基本概念、公式等知识点的现象,我在复习课伊始出示了长30cm、40cm的两根铁丝。
教学环节1:
问题(1):以30cm、40cm两根铁丝为条件,你能够想出哪些平面图形?
问题(2):如何利用平移、旋转得到圆柱体和圆锥体?
……
“复习课就是要我们做题目”,对于问题(1),学生的惯性思维被两根铁丝给打破了,真是不破不立。全班学生个个劲头十足地在草稿纸上作图,但大多画的是平面的角、长方形、三角形和圆(如图1)等,学生复习的热情出乎我的意料。
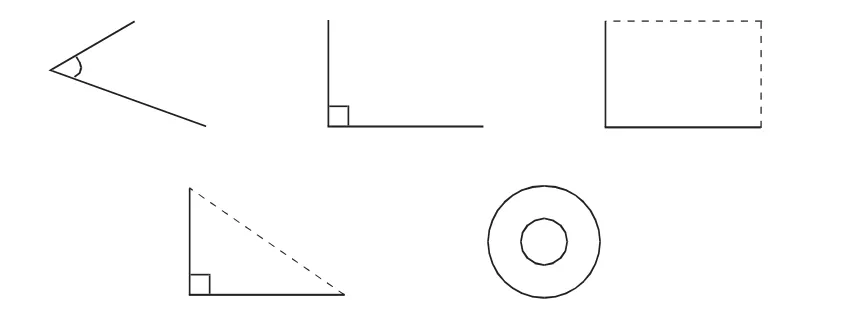
图1
但对于问题(2),有40%左右的学生犯难了,他们不是看天花板,就是咬笔头。我通过课件动态演示图形的变化过程(如图2),顿时学生的思维变得灵活起来,使学生真正理解了概念的基本元素。
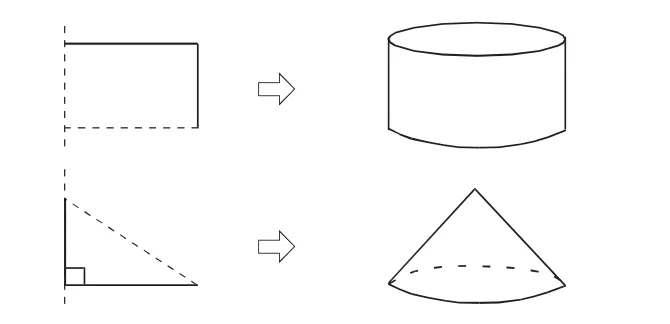
图2
二、重组技能技巧,激起学生潜心复习
为延展两根铁丝的空间想象,也为突破难点、疑点问题的解决,我再引导学生从经历想象到画图的过程。
教学环节2:
问题(3):你能依照铁丝的长度画出圆柱、圆锥吗?
问题(4):你认为按图3旋转得到的两个圆柱体的体积、侧面积相等吗?(生先猜测答案)
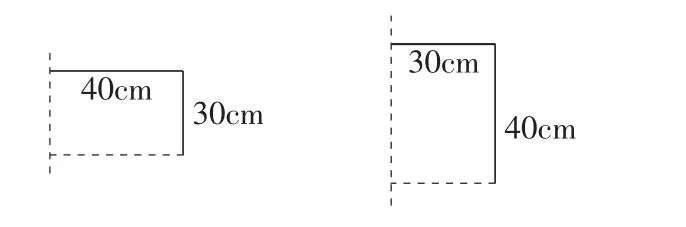
图3
课堂上先让学生自己画图并计算圆柱体的体积、侧面积,再让学生交流,最后由学生集体作出评价(课件相应展示图形及计算过程)。问题(4)列式为V1=π402×30、V2=π302×40,从列式中可以发现这两个圆柱体的体积不可能相等,从而推出这两个圆柱体的表面积也不同。
有很大一部分学生误认为这两个圆柱体的体积是相等的,且表面积也是相等的,但通过演算得出其体积和表面积均不相等,使得这些学生的疑点问题得到解释,难点也随之突破。
教学环节3:
问题(5):你认为按图4旋转而得的两个圆锥的体积相等吗?
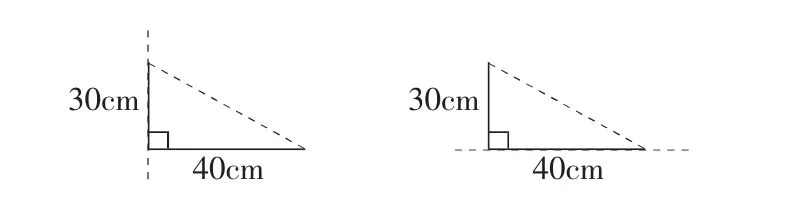
图4
问题(5)是很多学生百思不得其解的难点问题,因为大多数学生对以垂直轴线旋转的圆锥体(图5)认同度较高,而对以水平轴线旋转的圆锥体(图6)没有想象到。
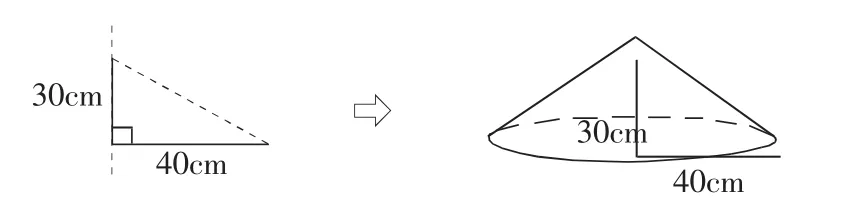
图5
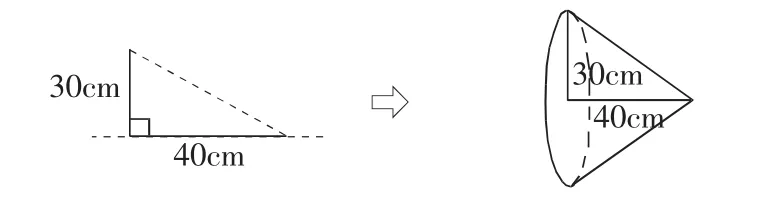
图6
为了把学习的主动权交给学生,特别是交给有疑惑、有问题的学生,通过个体的计算和全体学生的参与评价,学生能明确以水平轴线与垂直轴线旋转所形成的圆锥的体积不会相同。
三、重塑主体框架,激活学生的解题思路
在引导学生建立图形的主体框架时,用以下四个图示(图7、图8、图9、图10)进行比对。
教学环节4:
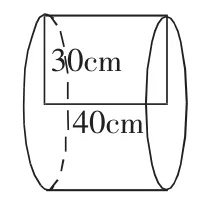
图7
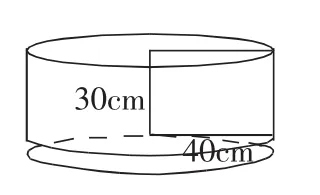
图8
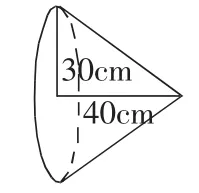
图9
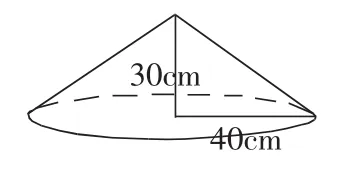
图10
图7与图9的圆锥等底等高,图8与图10的圆锥等底等高,使学生进一步明确了本节课复习的重要内容是八个字,即“等底等高,三分之一”。随后我设计了生活实例的题目,如下:“(1)自找一个圆柱、圆锥,量出必要的数据,计算出体积。(2)一个圆柱的侧面积是471平方厘米,高是15厘米,求圆柱的底面半径是多少厘米?(3)一个圆柱形的灯笼,底面直径是24厘米,高是30厘米。在灯笼的下底和侧面糊上彩纸,至少要多少平方厘米的彩纸?”
题目的数量数不胜数,题目的形式千变万化,但学生若能真正掌握灵动的思想方法,在圆柱、圆锥的体积计算中或在圆柱表面积计算中能把握“等底等高,三分之一”的要旨,再加上与实际(如上题的灯笼只算一个底面)情况的分析,那么学生的解题能力一定会有明显的提升。
四、重开智慧大门,激励学生认真应对
在教学实践和访谈调查中,我发现学生对圆柱、圆锥相关的综合题普遍存在着畏惧感。因此,我在复习课的最后环节往往设计应用广泛且需要一定综合思维能力去解决的题目,对学生进行训练。
教学环节5:
(1)切出来的问题。
王师傅要将一根长12分米的圆柱形钢条平行于底面切成不均匀的3段,表面积增加了12.56平方分米,原来这根钢条的体积是多少立方分米?
(2)削出来的问题。
王师傅将其中一根圆柱形钢条削成一个最大的圆锥,其中削去了12.56立方分米,那么这根钢条原来的体积是多少立方分米?
(3)铸出来的问题。
王师傅打算将另一根12.56立方分米的圆柱形钢条铸成一个底面积是5立方分米的圆锥,那么圆锥的高度会有多少呢?
理清了知识脉络,不代表完成了复习任务。有效的复习,还需要有效的练习来支撑。“整理与复习”课的知识涵盖力求全面,题目设计需精准取舍。如有关圆柱与圆锥的练习题不计其数,可上述三道题目具有较强的代表性,“切、削、铸”的问题虽然只有一字之差,但在数学题中的意思却完全不一样。课堂教学中,我以这三道题为切入点,引领学生根据题目仔细思考、辨析,找到合适的解题思路,同时让学生感受到体积、表面积之间变与不变的关系。其中,“铸出来的问题”是这三道题中较难的一题,在实际教学中很多学生都会忘记用圆柱体积除以三分之一。通过这种对比的题组练习,既能在视觉上激发学生的思考,又为学生尽快找到解题策略、揭示解题规律提供了一条捷径。
近几年来,我在“整理与复习”课中采用了重温知识、重组技能、重塑框架、重开大门的“四重”环节,取得了较理想的复习教学效果。复习课并无固定的教学模式,以激发学生的复习信心和兴趣为主。正如赞可夫所说:“扎实地掌握知识,与其说是靠多次的重复,不如说是靠内部的诱因,靠学生的情绪状况而达到的。教学法一旦触及学生的情绪和意志领域,触及学生的精神需要,这种教学法就能发挥高度有效的作用。”
(责编蓝天)
[中图分类号]G623.5
[文献标识码]A
[文章编号]1007-9068(2016)01-019

