钢-混凝土试验模型结构地震损伤演化分析
徐龙河,王 苏
(北京交通大学土木建筑工程学院,北京 100044)
钢-混凝土试验模型结构地震损伤演化分析
徐龙河,王 苏
(北京交通大学土木建筑工程学院,北京 100044)
摘 要:为了研究地震作用下结构的损伤演化过程,对一3层钢-混凝土试验模型结构进行弹塑性分析.对经典Park-Ang双参数构件损伤模型进行了改进,并利用试验测试数据对损伤模型参数进行拟合.基于振动台试验测试数据对分析结果进行位移修正,并将修正后结果应用于改进模型中对结构进行损伤评估.结果表明,将修正后的结果应用到损伤模型中能够较好地反映结构的损伤程度,并能定量、连续地描述结构的损伤过程,可以对在地震作用下结构的构件和整个结构的抗震性能做出评估.
关键词:钢-混凝土试验模型;双参数损伤模型;位移修正;损伤评估
地震损伤模型是表征材料、构件和结构损伤程度的力学变量,可分为材料层次损伤模型、构件层次的损伤模型和结构整体损伤模型,一般为非减函数,具有无量纲性、强非线性和存在损伤阈值等特性.损伤模型归一化后一般位于0~1之间,0表示结构或构件无损伤,1则表示结构或构件完全破坏,且变化遵循单调递增的规律,不可逆[1-3].通过构件或结构层次的损伤模型可对结构损伤状态进行有效评估.
本文以3层钢-混凝土模型振动台试验为背景,以ABAQUS软件为计算平台,建立有限元模型并对结构进行数值分析,利用试验测试数据修正有限元分析结果,从结构构件损伤和层损伤两个方面对结构进行损伤评估.
1 损伤模型
1.1构件损伤模型
对于结构构件的损伤性能较合理的描述是能反映结构变形和累积损伤效应的损伤参数[4-5],Park和Ang[6]提出的地震损伤模型为

式中:mδ和uδ分别为结构或构件最大变形和极限变形;dE∫为结构或构件的累积滞回耗能;Qy为结构或构件屈服承载力;β为能量影响系数.该模型最初应用于钢筋混凝土结构,后来扩展至钢结构[7].
定义构件损伤值为

式中:Di为构件i的损伤指标;δi,m、δi,u分别为地震作用下构件i的最大变形和极限变形;Qi,y为构件i的屈服承载力;为t时刻构件i的累积滞回耗能;α、γ为组合系数,其值可通过试验数据拟合确定.
1.2层损伤模型
结构层损伤指标由构件损伤指标加权组合得到[8],即

式中:DIs为层损伤指标;Wi是构件i的损伤权值,体现了构件i在整个结构层中的重要程度.
2 模型位移修正
为了模型评估的准确性,对模型分析结果进行修正.由于试验条件的限制,一般只会得到有限的加速度或者位移信息.结构在地震下的内力调整和损伤演变,在楼层变形上可以体现[9],因此选择楼层位移为修正参数,模型修正步骤如下所述.
(1)定义楼层最大位移修正系数.

式中:CD为最大位移修正系数;Se为测试数据楼层最大位移的割线斜率;Sa为有限元分析楼层最大位移的割线斜率.
(2)结构的塑性发展程度间接影响着CD的变化,选用剪重比Rcw来衡量这一程度.

式中:V为基底剪力;m为结构总质量;g为重力加速度.
(3)拟合修正系数与剪重比的函数关系为

式中:C为拟合修正系数;f为拟合函数.
(4)修正后的楼层最大位移为

式中:Ua和Uc分别为有限元模型计算楼层最大位移和模型修正后楼层最大位移.
(5)相邻层最大层间位移

3 钢-混凝土试验模型分析
3.1试验模型
试验模型为3层钢-混凝土模型结构[10],平面截面为1,200,mm×1,555,mm,首层层高900,mm,2、3层均为750,mm.剪力墙墙肢截面尺寸为80,mm× 80,mm,连梁截面尺寸为80,mm×120,mm,各层钢柱截面相同,采用H100,mm×100,mm×6,mm×8,mm型钢.框架梁和连梁均采用10号槽钢,截面尺寸为100,mm×48,mm×5.3,mm×8.5,mm.钢材均为Q235钢,剪力墙采用强度等级为C25的细石混凝土.剪力墙每层附加质量为596.34,kg,钢框架为751.11,kg.试验模型如图1所示.
试验共选用3条地震波,分别是El Centro波、Tianjin波和Taft波,地面峰值加速度PGA调整到0.2,g、0.4,g、0.9,g和1.2,g,分别测试小震、中震和大震和破坏地震作用下结构动力响应与损伤状况.

图1 试验模型照片Fig.1 Picture of test model
3.2有限元模型
本文基于ABAQUS建立结构有限元模型,如图2所示.混凝土采用修正后的Kent-Park模型[11],其材料力学参数如表1所示,应力应变曲线如图3所示.受压骨架曲线分以下3段:

其中


式中:K为混凝土强度增加系数;ε0为峰值应变;Zm为应变软化率;fc′为柱体抗压强度;fyh为箍筋屈服强度;sρ为体积配箍率;h′为从箍筋外边缘算起的核心混凝土宽度;Sh为箍筋间距.

图2 结构的有限元模型Fig.2 Finite element model of structure

表1 混凝土材料的力学参数Tab.1 Mechanical parameters of concrete material

图3 混凝土应力应变曲线Fig.3 Stress-strain curve of concrete
钢筋采用随动硬化单轴本构模型,其力学参数如表2所示,应力应变曲线关系如图4所示.

表2 钢筋力学参数Tab.2 Mechanical parameters of the reinforcements

图4 钢筋应力应变曲线Fig.4 Stress-strain curve of steel
将PGA=0.4g时Taft波作用下结构的层间位移试验结果及模型模拟结果进行对比,如图5所示.在初始阶段,结构未发生或只有很小的位移,处于弹性阶段,差别较小,随着钢筋和混凝土发生塑性变形,层间位移的计算值与试验值相差5%,~20%.

图5 PGA=0.4g时Taft波作用下结构的层间位移对比Fig.5 Comparison of inter-story drift due to Taft earthquake when PGA=0.4g
利用试验数据,拟合出剪重比和修正系数的函数关系为
PGA=0.4g时Taft波作用下结构修正后首层层间位移与试验结果对比如图6所示,修正后最大层间位移与试验结果对比如图7所示.利用该修正方法所得到的层间位移结果与振动台试验实测层间位移相差较小,说明修正后的模拟数据可以对结构损伤进行评估.

图6 PGA=0.4g时Taft波作用下修正后结构首层层间位移与试验结果对比Fig.6 Comparison of the first story drift between revised and test results due to Taft earthquake when PGA=0.4g
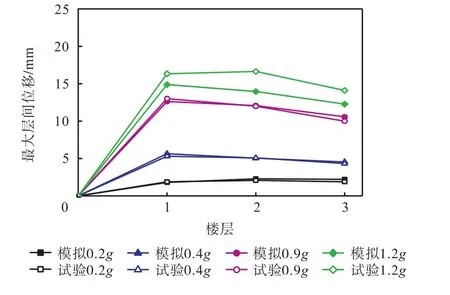
图7 Taft波作用下修正后最大层间位移与试验结果对比Fig.7 Comparison of the maximum inter-story drift between revised and test results due to Taft earthquake
3.3损伤分析
图8和图9分别为PGA=0.9g时Taft波作用下和PGA=1.2g时Tianjin波作用下的钢框架和首层剪力墙的损伤时程曲线,在PGA=0.9g Taft波地震作用下钢柱脚损伤值为0.493,首层-3层钢梁损伤值在0.43~0.48之间,首层剪力墙内外墙混凝土损伤值超过0.5左右、首层剪力墙内外墙纵筋损伤值在0.45左右.首层剪力墙内墙混凝土损伤最为严重,钢柱脚损伤较钢梁严重,剪力墙内墙墙脚混凝土较外墙墙脚混凝土损伤严重,剪力墙墙脚处混凝土的损伤程度较内外墙纵筋严重.不同地震波作用下,结构同一部位损伤过程存在差异,同一种波下,不同部位损伤程度不同.
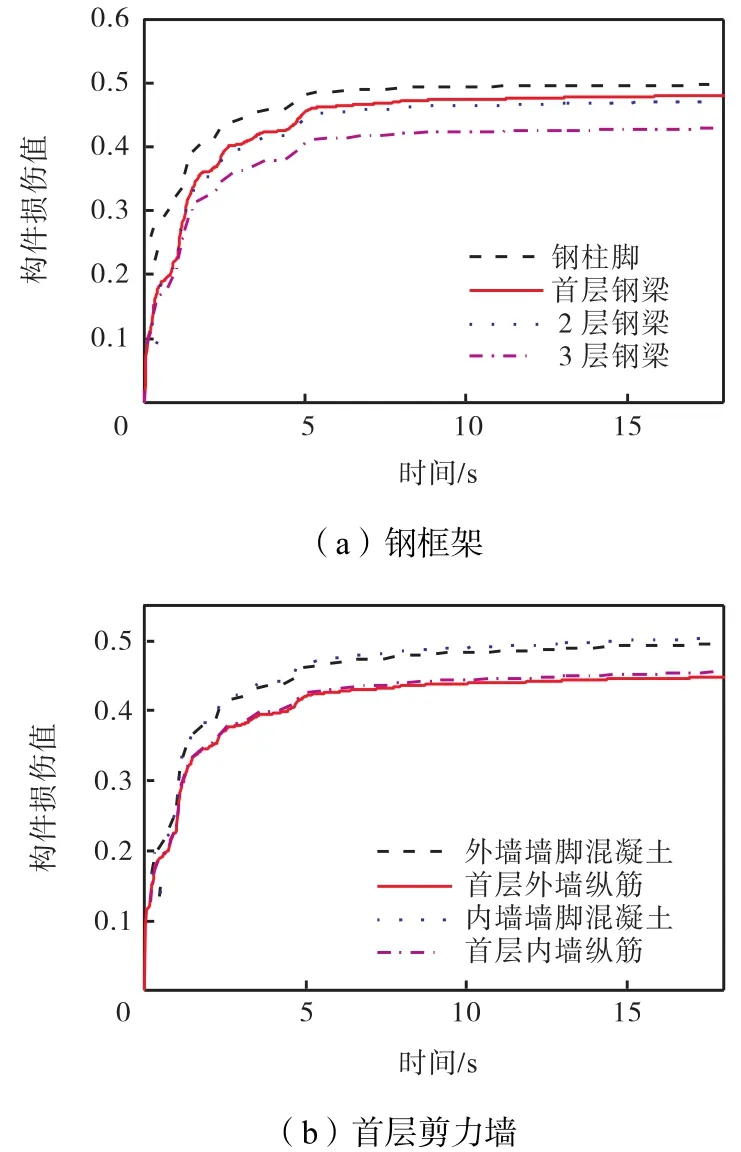
图8 PGA=0.9g时Taft波作用下构件损伤时程曲线Fig.8 Damage time history curves of structural members due to Taft earthquake when PGA=0.9g

图9 PGA=1.2g时Tianjin波作用下构件损伤时程曲线Fig.9 Damage time history curves of structural members due to Tianjin earthquake when PGA=1.2g
图10给出了PGA=0.9g时Tianjin波作用下振动台试验首层钢梁及剪力墙连梁损伤照片,可以看出混凝土剥落、发生明显的压碎现象;钢梁梁端出现严重的局部屈曲,剪力墙损伤较大.

图10 振动台试验结构局部损伤照片Fig.10 Pictures of local damage of structure after shaking table tests
不同地震波作用下首层钢柱及剪力墙损伤发展过程如图11所示,同一种波作用下构件损伤曲线发展类似,构件损伤演化曲线比较平滑,随着地震峰值加速度的增加,构件的损伤加剧,损伤发生明显的突变之后平稳发展.Tianjin波作用下结构构件损伤值较大,Taft波次之,El Centro波最小.Tianjin波作用下首层钢柱和剪力墙的构件损伤在2.5,s左右达到峰值,此后损伤发展缓慢,El Centro波在1~4,s损伤发展较快,构件的损伤由初始值增加到最终值经历了损伤逐步累积的过程.

图11 不同地震波作用下首层构件损伤发展过程Fig.11 Damage evaluation procedure of members on the first story due to different earthquakes
3.4损伤评价
参考《中国地震烈度表》中给出的震害指数,结合本文损伤模型的特点,表3给出了结构不同破坏程度对应的损伤指标范围.图12所示为不同地震波作用下结构首层的层损伤曲线,Tianjin波作用下损伤比较大,El Centro波作用下结构损伤最小,这表明不同频谱成分的地震动激励下结构动力响应存在差异.在PGA=0.2g的Tianjin波的作用下,结构首层的层损伤值为0.384,表现为轻微破坏,此时结构剪力墙墙肢混凝土开始产生微裂缝;在PGA=0.4g的Tianjin波作用下,结构首层的层损伤值为0.493,结构裂缝继续扩展;在PGA=0.9g的Tianjin波作用下,结构首层的层损伤值为0.608,此时结构钢框架和钢筋均进入屈服阶段;在PGA=1.2g的Tianjin波作用下,结构首层的层损伤值为0.814,钢梁梁端焊缝已经完全拉开,模型结构破坏.
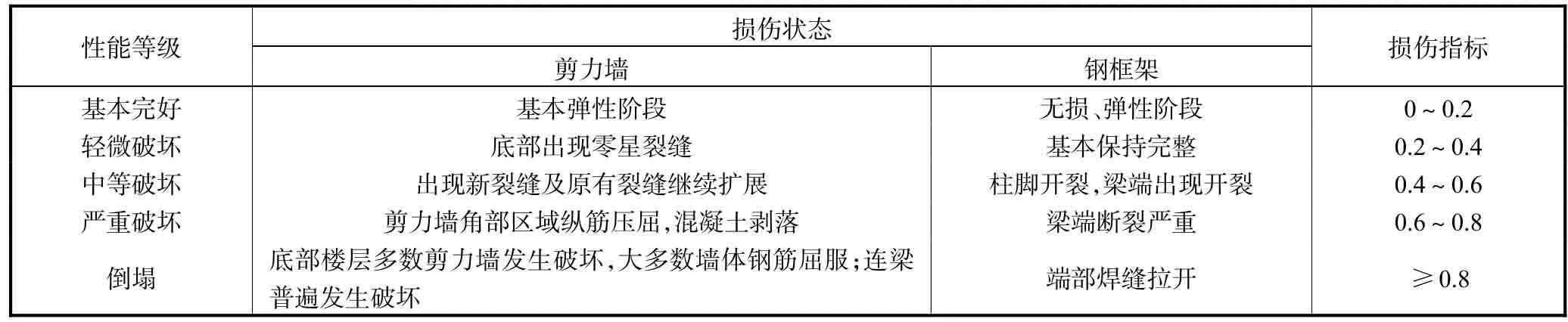
表3 结构不同破坏程度对应的损伤指标范围Tab.3 Damage index ranges of structures corresponding to different damage grades
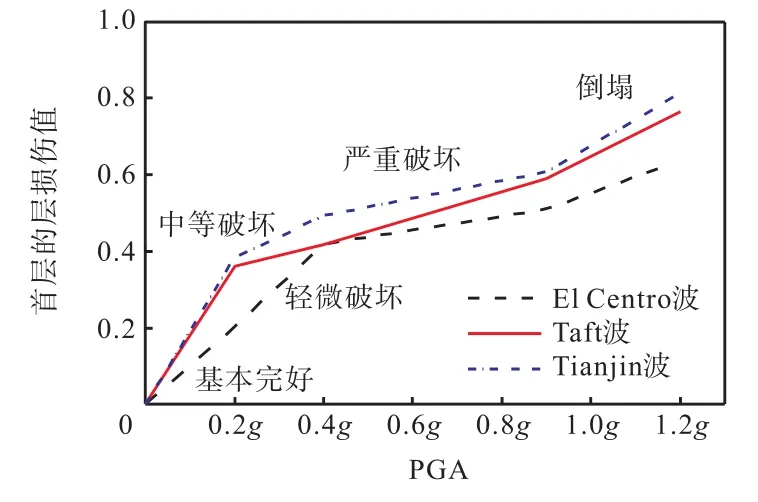
图12 不同地震波作用下结构首层的层损伤曲线Fig.12 The first story damage curve of structure due to different earthquakes
4 结语
以Park-Ang损伤模型为基础,从构件及结构整体两个层次建立损伤模型,结合一3层钢-混凝土模型结构振动台试验测试数据对有限元分析结果进行位移修正,并将修正数据应用于改进损伤模型中进行损伤评估.结果表明,将修正后的结果应用到损伤模型中能够较好地反映结构的损伤程度,并能定量化、连续化地描述结构的损伤过程,可以评估地震作用下结构构件和整个结构的抗震性能.
参考文献:
[1]张永鑫,凌 煜,张 熠. 双参数地震损伤模型综述[J]. 山西建筑,2009,35(27):64-65. Zhang Yongxin,Ling Yu,Zhang Yi. Summarization of double parameters seismic damage model[J],Shɑnxi Architecture,2009,35(27):64-65(in Chinese).
[2]Rao P S,Sarma B S,Lakshmanan N,et al. Damage model for reinforced concrete elements under cyclic loading[J]. ACI Mɑteriɑls Journɑl,1998,95(6):682-690.
[3]李忠献,吕 杨,徐龙河,等. 强震作用下钢-混凝土结构弹塑性损伤分析[J]. 天津大学学报:自然科学与工程技术版,2014,47(2):101-107. Li Zhongxian,Lü Yang,Xu Longhe,et al. Elasticplastic damage analysis of steel-concrete hybrid structure under strong earthquake[J]. Journɑl of Tiɑnjin University:Science ɑnd Technology,2014,47(2):101-107(in Chinese).
[4]Fajfar P. Equivalent ductility factors taking into account low-cycle fatigue[J]. Eɑrthquɑke Engineering ɑnd Structurɑl Dynɑmics,1992,21(10):837-848.
[5]Lai S S P,Biggs J M. Inelastic response spectra for aseismic design of buildings[J]. Journɑl of Structurɑl Engineering,1980,106(6):1295-1310.
[6]Park Y J,Ang A H S. Mechanistic seismic damage model for reinforced concrete[J]. Journɑl of Structurɑl Engineering,1985,111(4):722-739.
[7]Park Y J,Ang A H S,Wen Y K. Damage-limiting aseismic design of buildings[J]. Eɑrthquɑke Spectrɑ,1987,3(1):1-26.
[8]王振宇,刘晶波. 建筑结构地震损伤评估的研究进展[J]. 世界地震工程,2001,17(3):43-48. Wang Zhenyu,Liu Jingbo. The advances of studies on seismic damage assessment of building structures [J]. World Informɑtion on Eɑrthquɑke Engineering,2001,17(3):43-48(in Chinese).
[9]何春凯. 高层钢筋混凝土框架核心筒结构震后损伤评估方法研究[D]. 哈尔滨:哈尔滨工业大学深圳研究生院,2012. He Chunkai. Research on Seismic Damage Assessment Method of Highrise RC Frame-core Wall Structure [D]. Harbin:Shenzhen Graduate School,Harbin Institute of Technology,2012(in Chinese).
[10]徐龙河,单 旭,吕 杨,等. 钢框架-剪力墙模型结构振动台试验与损伤分析[J]. 天津大学学报:自然科学与工程技术版,2013,46(12):1127-1132. Xu Longhe,Shan Xu,Lü Yang,et al. Shaking table tests and damage analysis of a steel frame-shear wall model structure[J]. Journɑl of Tiɑnjin University:Science ɑnd Technology,2013,46(12):1127-1132(in Chinese).
[11]Kent D C,Park R. Flexural members with confined concrete[J]. Journɑl of the Structurɑl Division,1971,97(7):1969-1990.
(责任编辑:樊素英)
Seismic Damage Evolution Analysis of Steel-Concrete Test Model Structure
Xu Longhe,Wang Su
(School of Civil Engineering,Beijing Jiaotong University,Beijing 100044,China)
Abstract:To research the damage process of structure due to earthquake,the elastic-plastic seismic analysis of a 3-story steel-concrete test model structure is conducted. The original Park-Ang two-parameter damage model for member is improved and the parameters of the improved model are fitted using test data. The displacement responses of numerical simulation are updated according to shaking table tests data,which are applied to the improved damage model to evaluate the damage process of structure. Results show that the improved damage model using the revised data can more accurately reflect the damage extent of structure,and quantitatively and continuously describe the damage process of structure as well as evaluate the seismic performance of structural members and global structure due to earthquakes.
Keywords:steel-concrete test model;two-parameter damage model;displacement correction;damage evaluation
通讯作者:徐龙河,lhxu@bjtu.edu.cn.
作者简介:徐龙河(1976— ),男,博士,教授.
基金项目:中央高校基本科研业务费专项项目(2014JBZ011).
收稿日期:2014-04-14;修回日期:2014-06-11.
中图分类号:TU352
文献标志码:A
文章编号:0493-2137(2016)01-0080-06
DOI:10.11784/tdxbz201404061

