一种利用载波观测优化伪码测距精度的方法

王嘉伟 曾芳玲 郭靖蕾



一种利用载波观测优化伪码测距精度的方法

王嘉伟 曾芳玲 郭靖蕾

电子工程学院，安徽 合肥 230037

针对伪码测距精度较载波相位观测低，但载波测距又存在整周模糊问题，观测难度较大，提出一种利用载波平滑伪距测量的方法，该方法利用载波测距的载波相位测量值辅助提高伪码测距精度,同时，伪码测距又可以辅助载波相位的锁定，改善载波相位观测的效率和准确性，满足系统对实时性的要求。最后通过仿真实验验证了载波平滑伪距对伪距观测的改善。

伪码测距；载波测距；载波平滑伪距

伪码测距和载波测距已经成为现代空间测量领域中的两种最主要的测距方式，研究结果表明，伪码测距的观测噪音相对于载波相位观测噪音来说要大得多，同时它受多路径的影响程度也比载波相位观测更为严重，所以伪码测距的测量精度相对载波相位测量的精度来讲要低一些，但其优点是不具有整周模糊度。相比较而言，载波相位的测距精度通常是基于载波的整数倍波长而计算的，因此其测距精度较高。但在其测量过程中需要解算整周模糊度。而通常来说，模糊度的解算准确度较低，而且解算过程的时间也较长，这使载波相位测距在实际中的应用受到了限制。

本文介绍了伪码测距和载波测距的基本方法。利用载波测距的载波相位测量值作为辅助对伪码测距值实施相位平滑，提高伪码测距的精度，最后给出了载波相位平滑伪距前后的仿真结果对比图[1]。

1 基于伪码的双向测距原理

所谓伪码测距方法，即通过测量接收机接收到的伪码与本地伪码发生器产生的伪码之间的相位差，来获得伪码测距信号在空间中的传播时延，从而获得测距值的方法[1]。伪码测距的示意图如图1所示：

图1 伪码测距示意图

通过伪码测距的基本方程：

得出节点之间的距离。

伪码测距过程中获得的相位时延存在诸多误差的影响，从而导致利用伪码进行测距的精度较低。

2 基于载波相位的双向测距原理

载波相位观测测量，即通过测定载波信号在传播路径的相位变化来确定伪距的方法。通常发射的载波测距信号的频率很高，那么载波相位就会有较高的分辨率，因此，在载波相位测距过程中通过计算载波相位差，就能得到高精度的测距值[2]。

图2 载波相位测距示意图

伪码测量是载波相位测量的基础，为实现载波相位测量，应先进行对伪随机码的延迟锁定，从而来实现对伪码信号的跟踪。当跟踪成功以后，再利用载波锁相环进行相位锁定，锁定成功后，通过后续对载波相位的跟踪，对其载波相位变化的整周期数进行自动计数，之后在任意观测时刻，其总相差可以表示为：

由于一般用来测距的载波频率较高，因此载波相位测距方法相比于伪码测距方法具有很高的测距精度，但是它也有一定的缺陷。通常我们需要测量的距离都远远大于发射载波的波长，这时由于载波是没有任何标志的正弦波，就会产生载波相位整周模糊度的问题，限制了载波相位测距方法在实际中的应用。

3 载波相位平滑伪距

3.1 基本原理

载波相位平滑伪距是结合了伪码测距和载波相位测距各自优点的一种高精度测距方法。

在双向测距与时间同步测量系统中，同时利用伪码和载波相位进行测距[3]。

测距终端的接收机可以同时进行伪码测距和载波相位测距，它们的测量方程可以分别表示为：

…

将式（10）带入到式（9）中，那么得到的就是经过载波相位平滑后的伪距，可以表示为：

3.2 仿真验证

经过上述对载波相位平滑伪距原理的分析，我们知道，载波相位平滑伪距原理，就是利用高精度的载波相位测量值作为辅助，进行多点采样和平滑滤波，平均了伪码测量值中的大部分随机误差，从而提高了伪距观测的精度[5]。

3.2.1 静态节点的算法仿真

对于两个静态节点来说，它们之间的距离不会改变，影响测距精度的原因在于传输信道上的噪音以及发送和接收设备的时延。仿真条件如下，设两节点相距100 m，选取码速率为5 MHz，则一个码元的宽度为0.2，码元长度为60 m，设相关精度为码元宽度的5%，则伪码测距误差约为3 m；设载波频率为70 MHz，一个载波周期约为14.3 ns，波长约为4.3 m，设相位测距误差为0.4 m。

按照上述仿真条件设计仿真实验，设随机误差服从零均值的正态分布，仿真实验的结果如图3所示，为了方便比较，图中所示为平滑前后测得的伪距值与真实值之差。

图3 平滑前后的伪距值

由图3可以看出平滑后的伪距测量值已经得到了明显的改善，十分贴近真实值。

双向时间同步系统在提高精度的同时还需要满足系统对实时性的要求，为此需分析平滑次数与精度间的关系。仿真实验中，分别进行了平滑次数M=5、M=10、M=50、M=100、M=150、M=200、M=250和M=300时的平滑前后的伪距值比较，并得出对应平滑次数的均方根误差，其对比分析结果如表1所示。

表1 平滑次数与测距精度的关系

由图表1中的数据比较可知，载波相位平滑前后的伪距误差随着平滑次数M的不断增大而不断减小。经过平滑次数M=300的平滑，其伪距误差值从原始的1.3652 已经降低到0.9389。图3所示就是选取M=200对伪距进行平滑的结果。

3.2.2 动态节点的算法仿真

对于动态节点，误差不仅来自于传输信道和设备时延，还要考虑相对速度对观测的影响。假设节点间处于低速运动状态，不考虑多普勒频的影响，只考虑相对运动对观测数据的影响。给出仿真条件，假设两同步节点相距100 m，并以0.1 m/s的相对速度分离，仿真条件如下，设两节点相距100 m，选取码速率为5 MHz，设载波频率为70 MHz，观测精度如前。得出了如图4和图5所示的载波相位平滑伪距前后的对比图。

图4 实测与平滑后伪距比较图

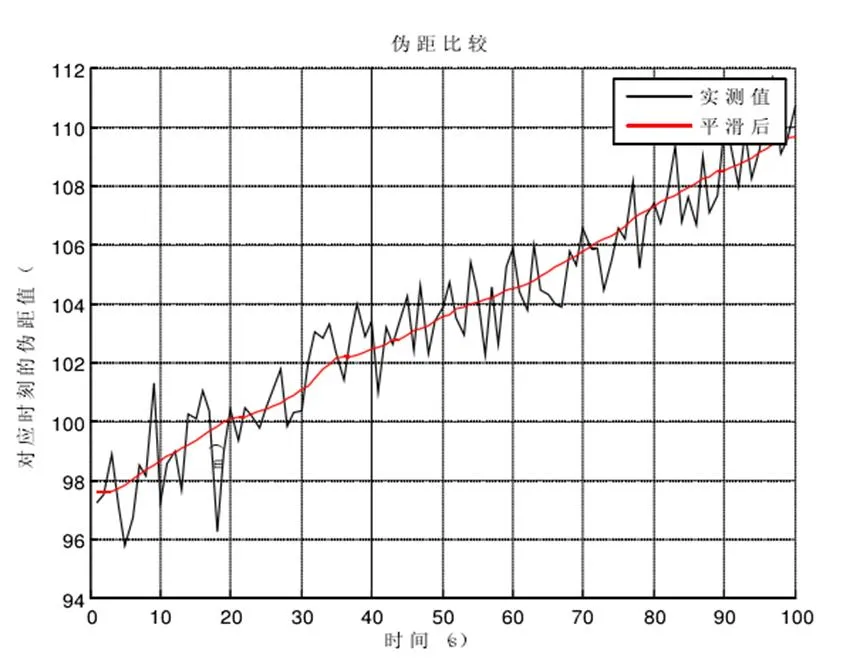
图5 伪距比较图（放大）

图4和图5所示的是采用伪距数据平滑前后的一个实例。为了更清楚地看到平滑后的效果，图5是从图4中截取的一段数据。由图可以看出，平滑后的伪距差值与平滑前的伪距差值相比，已经有了很大的改善。

利用同一组数据重复进行300次载波相位 平滑处理，分别计算出每一次仿真试验的伪距误差，并对其进行了拟合处理，得出了平滑次数与伪距误差之间的关系，如图6所示：

图6 动态节点伪距误差

仿真结果表明，载波平滑伪距确实可以得到比伪码测距更为精确的伪距值。但是平滑次数除了是载波相位平滑伪距的效果的决定因素以外，还是决定平滑时间的因素。换句话说，M的取值越大则相应的平滑时间就越长，就越难满足系统的实时性要求。因此，在实际中，我们必须在平滑的效果和系统的实时性要求之间进行权衡和取舍，得出最合适的载波相位平滑的平滑长度。

4 结束语

本文对载波相位平滑伪距这一方法进行了介绍，利用Matlab进行了仿真。证明了载波相位平滑伪距的方法在满足系统实时性的前提下，确实提高了测距精度。

这也为提高分布式系统的授时精度提供了新的思路，在主从节点进行信号传输时，利用系统本身发射信号的载波对伪码测距进行平滑，得到更为精确的伪距值，由此提高授时精度，值得深入的研究。

[1]何丹娜，张天骐，高丽，等.二次调频一伪码调相复合信号的伪码盲估计[J].电子技术应用，2013，39（5）：100-103.

[2]梁保卫，涂海洋.大多普勒条件下伪码快捕技术[J].无线电工程，2014（8）：85-89.

[3]王徐华，柏鹏，李明阳，等.基于最小二乘法的高动态条件下抗频偏的精确同步方法[J].电子与信息学报，2012（11）：2755-2760.

[4]李井源，朱祥维，王飞雪.利用多相关器的伪码测距多址干扰抑制算法性能分析[J].信号处理，2014（12）：1510-1516.

[5]孙旭飞，李家生.双伪码直序扩频通信方法及抗干扰仿真分析[J].福州大学学报：自然科学版，2011（6）：878-882.

Method for Optimizing Pseudo Code Ranging Accuracy by Carrier Observation

Wang Jiawei Zeng Fangling Guo Jinglei

Electronic Engineering Institute, Anhui Hefei 230037

In view of the low precision of the pseudo code ranging, the carrier ranging and the ambiguity of the whole week, the observation is very difficult, a method using carrier smoothing pseudo range measurement is proposed. The method of using carrier phase measurement values to improve carrier ranging pseudo code ranging precision, and at the same time, pseudo code ranging can lock the auxiliary carrier phase, improve the efficiency and accuracy of carrier phase observation, meet the requirement of real-time system. In the end of the paper, the simulation results show the improvement of the carrier smoothing pseudo range to the pseudo range observation.

pseudo code ranging; carrier ranging; carrier smoothing pseudo range

V241.4

A

1009-6434（2016）10-0153-04

王嘉伟（1991—），男，汉族，籍贯（精确到市）为安徽合肥，学历为硕士研究生，研究方向为导航与授时。