基于机械臂辅助的相机标定研究
金广智,石林锁,司海峰,刘均超,刘 浩
(1.第二炮兵工程大学 五系,西安 710025; 2.西安思源学院,西安 710038;3.中航工业西安航空动力控制科技有限公司,西安 700077)
基于机械臂辅助的相机标定研究
金广智1,石林锁1,司海峰2,刘均超3,刘浩1
(1.第二炮兵工程大学 五系,西安710025; 2.西安思源学院,西安710038;3.中航工业西安航空动力控制科技有限公司,西安700077)
摘要:随着变焦镜头摄像机越来越多地被应用于计算机视觉的各个领域,其内部参数与放大倍数的关系的准确获知就显得尤为重要;采用建立内部参数与放大倍数之间函数关系的方式来构造参数模型;为了提高各放大倍数状态下的标定速度,采用舵机驱动的多自由度机械臂并由程序根据标定进程来灵活控制标定模板的移动位置,减少了人工干预;在通过张正友标定算法得到一系列离散的参数值后,采用了3种不同的拟合函数对其进行曲线拟合,并给出了各种方法的拟合效果及误差对比;通过该方法,可以有效建立起镜头的参数模型,为视觉分析提供准确的参数信息。
关键词:计算机视觉;变焦镜头;标定;机械臂;曲线拟合
0引言
近年来,变焦镜头摄像机越来越广泛地被应用于监控及工业检测等各种场合,如PTZ摄像机。相对于固定焦距摄像机,变焦镜头摄像机即可工作于短焦距状态用于大范围的监视与警戒,也可工作于长焦距状态用于重点区域的远距离监控[1]。安装有变焦镜头的PTZ摄像机由于具有良好的可操控性,因而被广泛用精确的自动跟踪[2-3]、大场景的深度重建[4]和标定测量[5]等领域。
将变焦镜头应用于机器视觉时,需要知道镜头准确的焦距、主点位置、畸变等参数。由于变焦镜头的放大倍数可以视为连续可变的。因此,如何得到工作在特定放大倍数下的镜头的各项参数成为变焦镜头的一个重要研究内容。文献[6-7]通过建立场景特征点,并采取实时标定的方法来获取镜头的焦距参数,虽然使用灵活,但精度无法得到保证,并且该方法受环境的极大制约,且无法获取除焦距以外的其他参数;文献[8]采用场景中的消隐点来得到近似焦距,仍然存在精度不高和受环境影响大的缺点;文献[9]对主点和焦距采取了分开标定的方法,并假设镜头的不存在畸变参数,忽视了对处于低放大倍数状态的镜头的畸变较大的问题;文献[10]对所有放大倍数下的焦距、主点等参数进行了分析,并建立了各参数与放大倍数之间的函数关系。本文对焦距、主点坐标、畸变等参数进行了张正友标定算法进行标定,由于该算法对于每个放大倍数的标定都需要采集一定数量的标定模板图像,在放大倍数档位较多的情况下,需要大量手工移动标定模板的操作。为了加快标定速度,减少人工操作,本文使用了机械臂来固定标定模板,借助机械臂的运动功能来代替手工移动标定模板。通过控制板的驱动程序,可以根据标定进程由程序同步控制机械臂的运动状态,实现一定程度上的自动标定。该方法极大地减少了人工干预,有效缩短了标定时间。
文献[11]给出了各个参数随放大倍数的变化关系,但没有给出函数拟合结果;为了建立精确的放大倍数与各项参数之间的函数关系,文献[9,10]对焦距参数进行了曲线拟合,但没有考虑其他参数的分布情况。在文献[9,10]的基础上,本文加入了切向畸变参数,并使用3种不同的拟合函数来对焦距、径向畸变、切向畸变参数进行拟合,并以SONY-D90P变焦摄像机为例,对比了各种拟合函数的拟合误差。
1基于参照物的参数标定方法
1.1摄像机模型
基于参照物的参数标定方法,首先需要定义像素、图像、摄像机和世界4个坐标系,并在小孔成像模型和非线性畸变模型基础上建立起4个坐标系的关系。
1.1.1小孔成像模型
图1为小孔成像模型的示意图,Oc点为摄像机的光心,OcXcYcZc为摄像机坐标系,OwXwYwZw为世界坐标系,O1xy为图像坐标系,Opuv为像素坐标系。OcO1为摄像机的焦距。
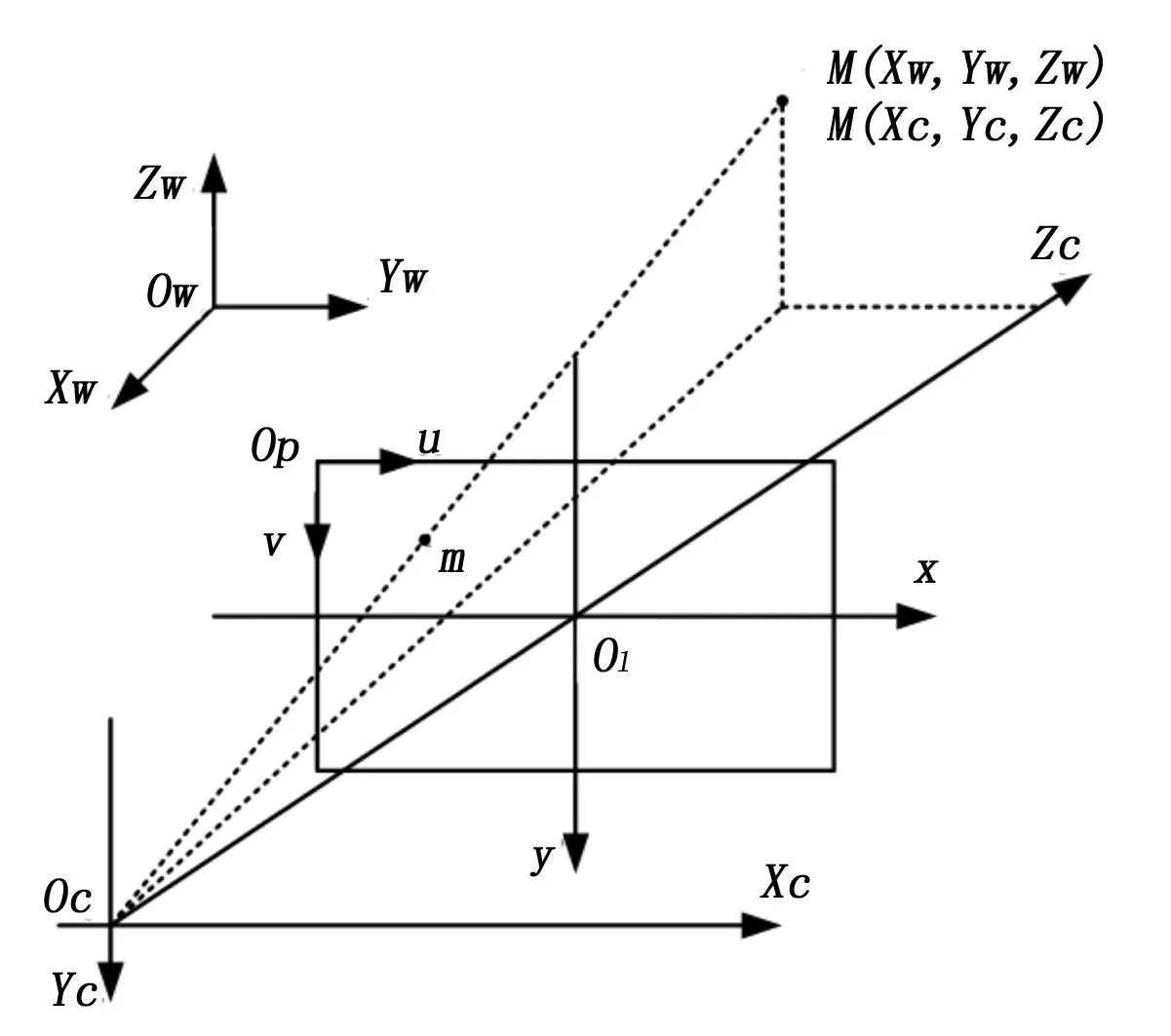
图1 标定所使用的各参考坐标系
可得如下的关系式:
(1)
其中:s为所有参数的一个尺度因子。R和t分别为摄像机坐标相对世界坐标的旋转矩阵和位移矩阵。式(1)也可用式(2)展开:
(2)
1.1.2非线性畸变模型
通常镜头会产生畸变,包括径向畸变和切向畸变,因此,加入畸变后的投影公式可以改写为式(3):
(3)
因此,我们需要通过标定得到8个未知数,它们分别是焦距fx和fy、主点坐标cx和cy以及径向畸变k1和k2和切向畸变p1和p2。
1.2基于二维平面参照物的标定方法
基于参照物的参数标定方法主要有利用最优化算法[12]的标定法和Tsai的两步标定法[13]和张正友的二维平面模板标定法[14]。最优化算法的标定法由于需要给定初值以及优化程序比较复杂而应用并不广泛;两步标定法虽然精度较高,但它对三维标定物的制作精度及检测精度要求也比较高。张正友提出的二维平面模板作为参照物进行标定的方法,因其模板制作简单和算法速度快而受到广泛的应用。张正友标定方法主要包括以下几个步骤:
1)制作所角点坐标参数已知的二维平面标定模板;
2)获取标定模板在不同位置的摄像机图像;
3)检测每幅图像的角点,并与原始模板建立对应关系;
4)利用检测到的角点坐标与原始模板已知的坐标参数估计摄像机参数的解析解;
5)通过最小二乘法解出偏转参数;
6)利用非线性规划方法迭代求出精确解。
为了进一步提高精度要,减少图像噪声带来的误差干扰,通常需要采集10张以上的标定模板图像进行标定。
2多自由度机械臂辅助标定
由于变焦镜头的标定需要确定镜头焦距等参数与控制参数之间的对应关系,通常需要得到不同控制参数下的对应的镜头参数,并建立两者之间的映射关系。因此,我们需要对多组不同参数情况下的镜头图像进行标定,这需要大量的重复工作。假设每一次标定需要使用N张标定图像,共有Cz个放大倍数档位,则标定人员需要移动标定模板N×Cz次,以N=15,Cz=20为例,则需要300次。为了提高标定速度,减少人为操作。本文提出了一种自动控制标定模板运动的方法,该方法以多自由度机械臂为平台,通过控制其运动来得到不同的标定模板位置,通常每个控制参数下需要十张以上的模板图像。
机械臂使用可以精确控制舵机作为关节运动组件,如图2(a)所示,每个关节可以转动180°以上。标定模板固定在机械臂最末一个关节上,如图2(b)所示,借助机械手的多自由度运动功能,转动标定标定模板至任何期望的位置,减少了以往人工移动标定模板的操作及固定困难的问题。由于张正友标定算法并不关系标定模板与镜头的相对位置关系,因此,机械臂并不需要精确的运动参数,只要固定于其上的标定模板能完全位于成像中并且所有的角点能被正确检测到即可。

图2 机械臂结构与标定模板的安装
2.2标定过程中机械臂的运动控制方案
机械臂的控制有专用的驱动板通过串口通讯来实现,由于机械臂控制板可以实现多种组合操作,因此可以提供以下3种组合程度由低至高的标定模板运动方案:
1)全部手动操作控制标定模板运动,通过控制每一个舵机的转动角度,来实现不同的姿势,达到移动标定模板的目的;
2)使用动作组功能,通过预先设计好的舵机角度组合得到对应的标定模板位置,标定时人工选择对应的动作组来进行获取标定图像;
3)通过预先设定的动作组,由标定算法程序与舵机控制板直接通讯,实现自动标定。
为了加快标定速度,本文采用了方式3)的控制方案,其流程如图X所示。在得到每一幅标定图像以后,首先对标定模板进行角点检测,如果角点检测成功且与预设的模板相匹配,则控制机械臂带动标定模板转动至下一个位置,重复该过程。可以设计冗余的标定模板位置动作组,保证最终每个镜头控制参数下的标定图像数目达到预设的最低个数。
1.5.1 药物治疗有效率 本研究以骨折发生率作为评估治疗效果的指标。原发性骨质疏松症防治的终点目标是降低骨折发生率,因而主要探讨治疗药物在防治骨质疏松性骨折的优势。芪骨胶囊方案组和仙灵骨葆胶囊方案组的骨折发生率来自于《密骨胶囊治疗原发性骨质疏松症Ⅲ期临床试验》[6]。有效率为未发生骨折患者人数占总治疗人数的比例。
与固定焦距镜头不同,变焦镜头的标定需要得到多组标定图像,因此,机械臂的使用可以大大标定速度,只要提前定义好动作组,程序即可自动运行,得到该变倍参数下的所有镜头参数。
2.3标定流程
使用机械臂辅助标定的流程如图3、4所示,其中图4为图3中带阴影过程块的具体步骤。需要说明的是,由于大变焦镜头的焦距覆盖范围较广,机械臂由于关节长度的限制不可能在所有放大倍数下都能将标定模板置于摄像机视野范围内,因此需要在每调节几档放大倍数后适当移动机械臂的位置,以保证标定模板被摄像机完整拍摄。
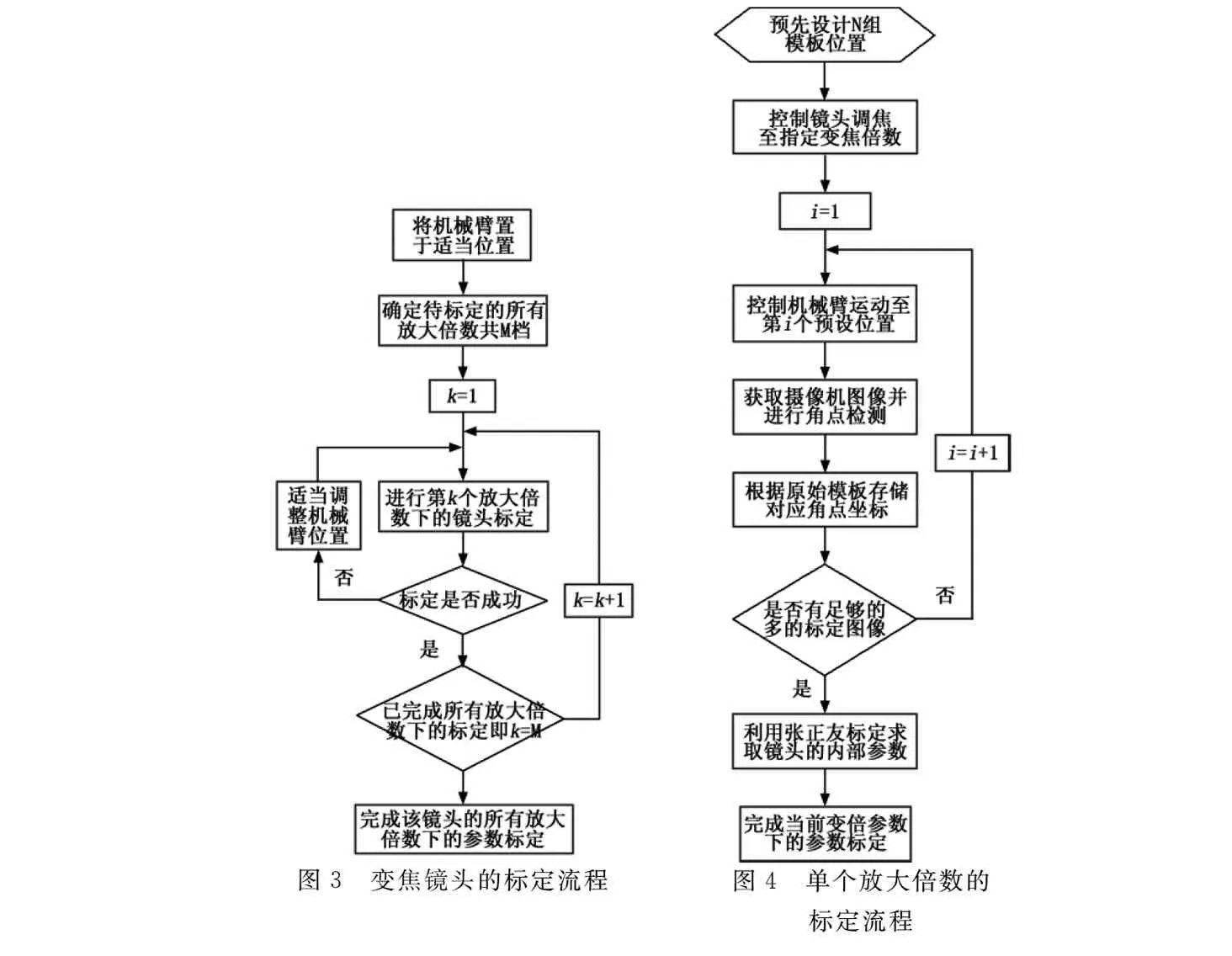
图3 变焦镜头的标定流程图4 单个放大倍数的标定流程
3变焦镜头参数的曲线拟合
变焦镜头的标定是在一组离散的变倍参数下进行的,为了得到连续的变倍参数与镜头参数之间的关系,本文对其进行了曲线拟合,以期得到以变倍参数为自变量,各镜头参数为因变量的函数。
3.1主点的坐标估计
通过图5可以看出,主点坐标可以视为常数值,其值在全焦距范围内保持恒定。本文采用求取平均值的方式来确定主点的坐标,如式(4):
(4)


图5主点坐标随放大倍数的变化曲线
3.2拟合函数的选择
文献[9]对所有镜头参数均采用了四阶多项式拟合,没有根据各参数的变化趋势进行具体考虑。为了提高精度,降低拟合结果的和方差(SSE)和均方根误差(RMSE),其定义如式(5)、(6)。接下来本文将以SONYD90P摄像机为例,对广大倍数从0~20倍进行了标定,得到各项参数,并用3种不同的拟合函数进行了拟合试验。
(5)
(6)
本文分别使用了如下形式的3种拟合函数:
1)指数函数(Exp2):y=aebx+cedx
其中阶数的选取是在多次试验后根据拟合效果及误差大小最终确定的。
3.3拟合试验对比分析

图6 参数fx的3种不同函数的曲线拟合及残差分析

图7 参数k1的3种不同函数的曲线拟合及残差分析
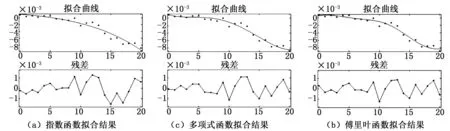
图8 参数p1的3种不同函数的曲线拟合及残差分析
图6~图8为分别采用三种拟合函数后的拟合效果与残差对比,图5的纵坐标分别代表SSE拟合值与RMSE误差值(pix),横坐标均为放大倍数。通过图6~图8的拟合效果和残差对比和表1的误差分析,可以看出与Poly4和相比Exp2拟合函数在多数情况下仅以4个系数的代价取得较好的拟合效果,仅对于k1这个变化趋势接近直线的参数没有得到有效的拟合结果;Fourier3具有最好的拟合性能,但其付出了系数较多代价(Fourier3需要8个参数)。
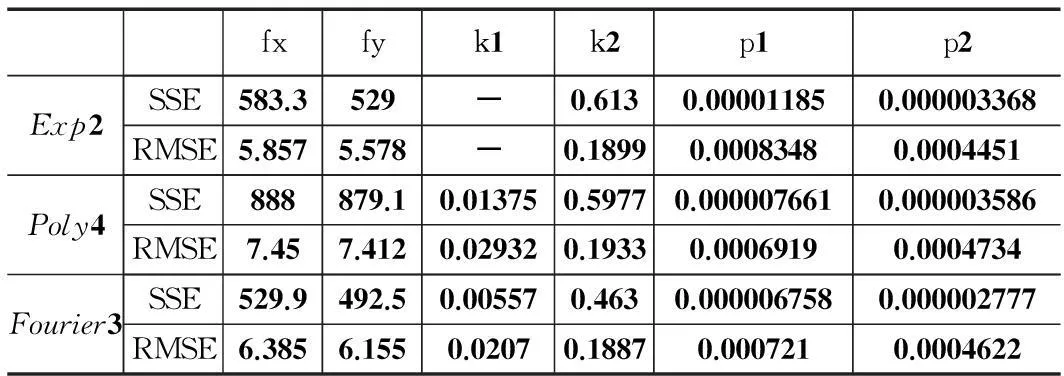
表1 3种算法实时性能对比 ms
因此,在实际标定时,需要根据具体的镜头进行对比拟合实验,并在使用这些拟合结果函数时,根据系数的多少和精度的要求灵活选择最合适的拟合函数。另外,对于不同的参数还应具体考虑拟合函数的选择,例如k1参数的拟合函数就可以用最简单的直线函数代替。
4结论
建立内部参数与放大倍数之间的关系是变焦镜头在计算机视觉应用中的一个重要步骤,本文采用多自由度机械臂来控制标定模板的运动,减少了人工干预,通过标定得到一系列离散参数值,采用曲线拟合的方式建立起内部参数与放大倍数之间的函数关系。该方法精度高,标定速度快,可以快捷有效地建立起变焦镜头的内部参数变化模型。
参考文献:
[1]GansN,HuG,DixonW.KeepingmultipleobjectsinthefieldofviewofasinglePTZcamera[A].ProceedingsofAmericanControlConference[C].St.Louis,USA:IEEEPress, 2013: 5259-5264.
[2]ADelBimbo,LisantiG,MasiI,etal.Device-taggedfeature-basedlocalizationandmappingofwideareaswithaptzcamera[A].ProceedingsofIEEEComputerSocietyConferenceonComputerVisionandPatternRecognitionWorkshops[C].SanFrancisco,USA:IEEEPress, 2010: 39-44.
[3]BimboAD,DiniF,LisantiG,etal.Exploitingdistinctivevisuallandmarkmapsinpan-tilt-zoomcameranetworks[J].ComputerVisionandImageUnderstanding, 2014, 114 (6): 611-623.
[4]WanD,ZhouJ.StereovisionusingtwoPTZcameras[J].ComputerVisionandImageUnderstanding, 2013, 112 (2): 184-194.
[5] 张小苗, 尚洋, 于起峰. 单目变焦摄像机自运动的标定测量法[J]. 计算机工程, 2008, 34(3): 29-31.
[6]WuZ,RadkeRJ.Usingscenefeaturestoimprovewide-areavideosurveillance[A].ProceedingsofIEEEComputerSocietyConferenceonComputerVisionandPatternRecognitionWorkshops[C].RhodeIsland,USA:IEEEPress, 2012: 50-57.
[7]SinhaSN,PollefeysM.Pan-tilt-zoomcameracalibrationandhigh-resolutionmosaicgeneration[J].ComputerVisionandImageUnderstanding, 2013, 103(3):170-183.
[8]SongKT,TaiJC.Dynamiccalibrationofpan-tilt-zoomcamerasfortrafficmonitoring[J].IEEETransactionsonSystems,Man,andCybernetics,2014, 36 (5): 1091-1103.
[9] 万定锐, 周杰. 双PTZ摄像机系统的标定[J]. 中国图象图形学报, 2012, 13(4): 786-793.
[10]TrajkovicM.InteractivecalibrationofaPTZcameraforsurveillanceapplications[A].ProceedingsofThe5thAsianConferenceonComputerVision[C].Melbourne,Australia:AFCVPress, 2013: 1-8.
[11]LiM,LavestJM.Someaspectsofzoomlenscameracalibration[J].PatternAnalysisandMachineIntelligence,1996, 18 (11): 1105-1110.
[12]FaigW.Calibrationofclose-rangephotogrammetricsystems:mathematicalformulation[J].Photogrammetricengineeringandremotesensing,1975, 41 (12):1479-1486.
[13]TsaiR.Aversatilecameracalibrationtechniqueforhigh-accuracy3Dmachinevisionmetrologyusingoff-the-shelfTVcamerasandlenses[J].IEEEJournalofRoboticsandAutomation, 1987, 3 (4): 323-344.
[14]ZhangZ.Aflexiblenewtechniqueforcameracalibration[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2000, 22(11): 1330-1334.
Manipulator Assisted Calibration and Parameter Curve Fitting for Zoom Lens
Jin Guangzhi1, Shi Linsuo1, Si Haifeng2, Liu Junchao3, Liu Hao1
(1.Second Artillery Engineering University, Xi’an710025,China; 2.Xi’an Siyuan University,Xi’an7100038,China; 3.China Avic Xian’ Aero-Engine Controls Technology Co,Xi’an700077,China)
Abstract:While the zoom lens cameras are increasingly used in various areas of computer vision, to accurately inform the relationship between the zoom values and the internal parameters is especially important. A parameter model using the function between zoom values and the internal parameters is proposed to express the relationship of them. In order to improve the calibration speed and reduce the manual intervention in different zoom state, servos driving manipulator is used and its movement is flexible controlled in accordance with the calibration process by the program. After a series of discrete parameter values are calibrated by Zhang zhenyou’s calibration algorithm, three different functions are used to fit the curve of the values, and fitting effect and error are also compared. Through the proposed method, parameter model of the zoom lens can be established which can provide accurate parameter information for further visual analysis.
Keywords:computer vision; zoom lens; calibration; manipulator; curve fitting
文章编号:1671-4598(2016)02-0186-04
DOI:10.16526/j.cnki.11-4762/tp.2016.02.051
中图分类号:TP391
文献标识码:A
作者简介:金广智(1987-),男,河北沧州人,博士研究生,主要从事模式识别、机器学习及计算机视觉方面的研究。石林锁(1958-),男,陕西凤翔人,教授,博士生导师,主要从事机器视觉、机电设备故障诊断等方面的研究。
基金项目:国家自然科学基金项目(F0111,F03048)。
收稿日期:2015-08-09;修回日期:2015-09-05。

