单调可测集合列外测度极限的性质及其应用

唐建国

（惠州学院数学与大数据学院，广东惠州 516007）

单调可测集合列外测度极限的性质及其应用

唐建国

（惠州学院数学与大数据学院，广东惠州 516007）

本文将外测度的有限可加性推广为外测度的可数可加性，紧接着利用它推导出递增可测集合列外测度极限的一个重要性质，对于递减可测集合列外测度的极限也有类似的性质.从这些性质出发，我们容易证明递增、递减、收敛及一般可测集合列测度极限的一系列重要结果，此时一列可测集合的并与交可测是其简单推论.

外测度；测度；可数可加性；可测集列；极限

1 引言

一般实变函数教材上先给出外测度的定义，再推导外测度的性质：非负性、单调性及次可数可加性，然后利用外测度给出可测集的定义如下[1-6]：

定义设E是Rq中的点集，如果对于任一点集T⊂Rq，都有

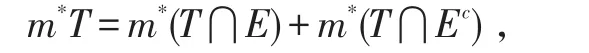
则称E是L可测的，其测度记为mE，且mE=m*E.

在可测集的定义中出现了两个集合E和T，为不致引起混淆，我们将定义中给定点集E称为被检验集，而任意点集T称为检验集.该定义是说对于任意检验集T，都被给定点集E分成两块T⋂E和T⋂Ec，而T的外测度要等于这两块的外测度之和.定义的条件看似十分简单，但因检验集T的个数无穷无尽，且是不可数无穷多个，因此需要验证不可数个等式.从可测集的定义及外测度的次可数可加性，容易看出当m*T=+∞时，定义中的等式显然是成立的，因此只需对m*T＜+∞的集T验证定义中的等式即可.根据［1］第3.2节的引理，检验集T可用Rq中的开区间来代替，结合m*T＜+∞可知，检验集T可用Rq中的有界开区间来代替，这样可大大减少检验集的个数.尽管如此，要验证的等式还是无穷无尽.因此除m*E=0等特殊情形外，直接按该定义验证一个给定点集E可测几乎是一件难以完成的事情.这说明按定义来验证点集可测不具有可操作性.主要原因是定义中所隐含的大量丰富的信息还没有被挖掘出来，这些信息将构成可测集的所有性质.只有从定义出发将可测集的性质全部挖掘出来，我们对可测集的认识才能比较全面准确而深刻.然后才可利用可测集的性质判定一个集合是否可测，即给出可测集合类，这是研究可测集的基本方法和路径.

在推导可测集性质时，文［1］从定义出发导出了可测集的两个简单充要条件，一个是与定义等价但表述方式有所不同，另一个是E可测当且仅当Ec可测.然后以并运算为主线索推导出了可测集关于并交差运算的性质，由两个可测集的并可测，推广到n个可测集的并可测，进一步推广到一列可测集的并仍可测.在证明n个可测集的并可测时，得到了如下外测度的有限可加性：当S1,S2,…,Sn可测且互不相交时，成立，这些外测度的有限可加性在证明一列可测集并可测时发挥了关键作用.

进一步分析发现，外测度的有限可加性可进一步推广为外测度的可数可加性.设是一列互不相交的可测集，则对有，紧接着利用它可推导出递增集合列外测度极限的一个重要性质：设是Rq的递增可测集合列，即，则对同样，对于递减集合列外测度的极限也有类似的性质.从递增递减集合列外测度性质出发，容易证明递增、递减、收敛及一般可测集合列测度极限的一系列性质，并将一列可测集合并与交可测作为其简单推论.

2 单调可测集合列外测度极限的性质

由此可得（5）式成立.在（5）式中取T=S即得（6）式.

注1从定理2的证明过程中可以看出，我们只需重新排列（7）式中各式子的顺序，即可由定理2证明定理1的结论，这说明定理1与定理2是完全等价的.定理1与定理2是同一个结论的两种表现形式，外测度可数可加性是用级数来表示，而递增集合列外测度极限的计算公式采用的是极限形式.这在实际应用中为我们提供两个选项，可根据问题所给条件选择一个比较方便应用的形式.

注2由定理3证明中的（11）式知，只要（11）式中的正项级数收敛，即可得到定理3的（8）式成立.要保证（11）式的正项级数收敛，除定理3中给出的条件m*T＜+∞外，还可有两个选项m*Sc＜+∞和存在正整数N使m*SN＜+∞.这三个条件只要有一个满足，（8）式就一定成立.定理3在证明递增递减可测集合列的测度极限定理时，将带来极大方便，特别对递减可测集合列，只需取一个特殊的m*T＜+∞代入即可得结果.

3 在单调可测集合列测度极限中的应用

在可测集的定义中，若m*T=+∞，则等式m*T=m*(T⋂E)+m*(T⋂Ec)显然成立.因此在证明集合可测时，仅需对m*T＜+∞的情形验证即可，在此情形下（8）式成立.

4 在一般可测集合列测度极限中的应用

本节应用单调可测集合列外测度极限的性质，得到收敛集合列测度极限的重要结论.对于更一般的可测集合列，应用该性质也推得了其测度上极限及下极限的有关不等式.

在（15）式的第一第二式中分别取T=S及

5 结语

本文在外测度已有理论的基础上，导出了单调可测集合列外测度极限的两个重要性质，即定理2和定理3.应用这两个定理容易证明一列可测集合的并或交可也可测，证明的思路是从特殊过渡到一般.我们先证明了单调增加可测集合列的并及单调减少可测集合列的交均可测，对这两种单调可测集合列均成立集合列极限的测度等于集合列测度的极限，即定理4和定理5.这时，可测集合列的并或交可测的结果就成为定理4和定理5的简单推论.此外，应用定理2和定理3我们证明了收敛可测集合列测度的极限定理，即证明了收敛集合列其极限的测度等于集合列测度的极限（定理6）.对于更一般的可测集合列（极限不一定存在），应用定理2和定理3容易推得集合列测度的上极限和下极限的有关不等式（定理7）.整个推导过程逻辑线条清晰，证明方法简便易行，显示了单调可测集合列外测度极限的性质在本文证明过程中的重要作用和优越性.

［1］程其襄，张奠宙，魏国强.实变函数与泛函分析基础［M］.第3版.北京：高等教育出版社，2013

［2］夏道行，严绍宗.实变函数与泛函分析［M］.第2版.北京：高等教育出版社，2010

［3］郑维行，王声望.实变函数与泛函分析概要［M］.第3版.北京：高等教育出版社，2004

［4］胡适耕.实变函数［M］.北京：高等教育出版社，2009

［5］徐森林.实变函数论［M］.第2版.北京：高等教育出版社，2001

［6］周民强.实变函数论［M］.北京：北京大学出版社，2001

【责任编辑：吴跃新】

Properties Related to the Limitation of Exterior Measure of a Monotonous Measurable Set Sequence and Its Applications

TANG Jian-guo
（School of Mathematics and Data Science，Huizhou University，Huizhou 516007，Guangdong China）

In this paper；we generalize the finite additive property of exterior measure to the countable and additive property of exterior measure；and then we deduce an important property related to the limitation of exterior measure of an increasing set sequence by using it.For a decreasing set sequence；there is a similar property related to the limitation of exterior measure.From these properties；we can easily prove a series of important results related to limitations of the measure of increasing；decreasing；convergence and general measurable set sequences.At this time；it is simple corollaries that union and intersection of a measurable set sequence are also measurable set.

exterior measure；measure；property of countable and additive；sequence of measurable set；limitation

O174.1

A

1671-5934（2016）04-0010-04

收搞日期：2016-08-18

广东省人才引进资金项目（A410.0204）；惠州学院科研项目（C511.0211）

唐建国（1965-），男，教授，博士，湖南永州人，研究方向为偏微分方程数值解等.