全光纤电流互感器λ/4波片的研制

惠 菲，崔 晶，左文龙，张书颖

(天津航海仪器研究所，天津300131)

全光纤电流互感器λ/4波片的研制

惠 菲，崔 晶，左文龙，张书颖

(天津航海仪器研究所，天津300131)

光纤λ/4波片的相位延迟量与对轴角度误差是光纤电流互感器最主要的误差源之一。研究通过琼斯矩阵分析法建立反射式光纤电流互感器的偏振光学模型，进而得到了相位延迟量与对轴角度误差和标度因数之间的关系，为误差补偿技术提供理论支持。并且进行了实际研制，使得1/4波片消光比可小于0.2dB。

λ/4波片；相位延迟量；光纤电流互感器

0 引言

随着电力工业的迅速发展，电力传输系统具有容量不断增加、运行电压等级越来越高的趋势，因此在高电压、大电流和强功率的电力系统中，传统电磁感应原理的电流互感器(简称为CT)暴露出了一系列严重的缺点，逐渐难以满足新一代电力系统在线检测、高精度故障诊断、电力数字网等发展的需要。

将光纤传感技术引入到电流检测中的光纤电流互感器[1](简称FOCT)成为解决上述难题的最好方法。与普通电磁互感器相比，FOCT具有抗电磁干扰能力强、频率响应范围宽、体积小、安装使用比较方便的特点，且没有磁饱和现象、铁磁共振和磁滞效应，因此成为目前国内外研究热点。

光纤电流互感器最为关键的两个器件为传感光纤与光纤λ/4波片，光纤传输线以及干涉光路需要使用偏振态稳定的线保偏光纤，传感光纤环需要使用圆保偏光纤，而光纤λ/4波片是用来进行线偏振光和圆偏振光变化的元件，它的误差将直接影响光纤互感器的性能。本文采用琼斯矩阵分析法，描述了反射式光纤电流互感器的偏振误差模型，在此基础上分析了光纤λ/4波片的对轴角度与相位延迟量误差对干涉仪性能的影响。

1 反射式光纤电流互感器

反射式光纤电流传感器[2]采用反射式的萨格纳克(Sagnac)干涉仪结构，其基本原理如图1所示。由光源发光经过单模光纤传输后，传送至起偏器，起偏为线偏振光，再经过45°熔接点分成两束偏振方向相互垂直的光，再由λ/4波片入射光转换为两个旋向相反(左旋和右旋)的圆偏振光，进入传感区域，经过一次法拉第效应后，到达反射镜发生反射，那么它们的偏振态便在反射时发生了交换，即原右旋光变成了左旋光，左旋光变成了右旋光。经过反射后，圆偏振光按原路返回经法拉第效应，然后通过λ/4波片转换回线偏振光，经过反射的光携带了相位差信息经过耦合器被传送至光电探测器。光路中，两束光都经过了保偏光纤的两个轴，以及传感光纤的左旋和右旋模式，所以说光路是完全互易的。而传感区域的磁场大小决定了相位差的大小。因为两束光都经历了两次法拉第效应，故而相位差为4倍的法拉第相移。

图1 全光纤电流互感器光路示意图Fig.1 Schematic diagram of FOCT

图1中，光经过反射镜返回至传感光纤，使偏转光旋转了90°，因而通过光纤线圈的正反偏振光相互正交，光纤中产生的附加线双折射得以相互抵消。然而法拉第效应是非互易的，所以光波正反两次通过光纤圈时，法拉第旋转效应不仅不能相互抵消，反而是加倍了。我们可以看到，这种结构不仅能够降低光纤线性双折射的影响，而且使法拉第效应加倍；同时，该反射式结构中，在同一根光纤中传输两束干涉光，可以有效降低外界因素(如温度、压力等)的干扰，亦不受Sagnac效应的影响；另外，该反射式结构所使用的光学器件相对较少、搭建较为容易，因此反射式结构与偏振旋转型和相位调制型结构相比，有着更高的灵敏度、更强的抗干扰能力、良好的稳定性等优点。但是在实际应用反射式结构时，两束正交偏振光波在同一根光纤中传输且同时受到调制，因此双轴调制器为优选。当调制器加上调制信号时，沿保偏光纤两个正交轴传播的线偏振光将引入与调制信号变化规律相同的相位差。

2 琼斯矩阵分析法

Jones矩阵利用Jones矢量来代表偏振光的电场矢量，并由场矢量Ex、Ey构成一个列矩阵。用Jones矩阵来分析偏振光，是一种简化光传输计算的方法。我们利用Jones矩阵来分析偏振光的传输，矩阵形式简练，只要进行最简单的矩阵运算，即可推算出经过偏振器件组成的复杂系统后的出射光波的状态，而其中每一过程的具体物理意义也不需要去追究了。

线偏振光[3]是指在传播过程中光矢量方向不变，其大小随相位变化而改变的光。这时在垂直于传播方向的平面上，光矢量端点的轨迹是一条直线。圆偏振光是指在传播过程中其光矢量的大小不变、方向规则变化，且其端点的轨迹是一个圆。椭圆偏振光的光矢量大小和方向在传播过程中变化规则，光矢量端点沿椭圆轨迹转动。任意一个偏振光都可以用两个振动方向互相垂直、相位有所关联的线偏振光来表示。

沿z轴传播的光波，则光矢量必然在垂直于z轴的x-y平面上振动，因此光可以表示为

E=E0cos(τ+δ0)

(1)

其中，τ=ωt-kz，δ0为初相位。

用分量的形式可以表示为

(2)

其中，δ1与δ2分别为x、y分量的初相位，取值不同可表示不同的偏振态。令初相位差δ=δ1-δ2，可以得到化简公式

(3)

设偏振光E的两个正交分量Ex与Ey的复振幅为：

(4)

(5)

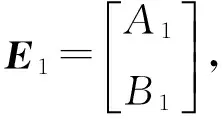
(6)

或

E2=GE1

(7)

其中，矩阵G为该偏振器件的琼斯矩阵，G的表达式可表示为

(8)

偏振光若依次通过了N个偏振器件，且用Gi来表示每个偏振器件的琼斯矩阵，出射光的琼斯矩阵则可以表示为

EN=GN…G3G2G1E1

(9)

通过以上的推论我们可以知道，利用偏振器件的琼斯矩阵可方便地算出偏振光通过偏振器件的出射光的状态。

3 反射式电流传感器的琼斯矩阵分析

由上面对Jones[4]的分析，可以对反射式电流传感器进行如下分析，设入射光为

(10)

已知，起偏器透光轴与x轴成45°，1/4相位延时器的快轴、慢轴与参考坐标系的x轴、y轴分别重合。在理想情况下，各个器件的Jones矩阵表示为：

起偏器为

(11)

45°熔接点为

(12)

调制器反射时为

(13)

λ/4波片为

(14)

入射时的Faraday效应为

(15)

反射镜为

(16)

反射时的Faraday效应为

(17)

入射时的调制器为

(18)

首先分析在没有调制器时的理论输出时，由Jones矩阵分析法分析，可以得到输出光的方程为

(19)

输出光强度为

(20)

式(20)即为反射型光纤电流传感器的理想模型。传感器的响应和相位差的余弦函数成正比。在实验中，相位差θ都很小，响应函数处在最不敏感的区域内，为了提高测量的准确度，通常要进行相位调制。通过对光波相位的动态调制，实现信息信号的传递，检测出相位差。

当到达探测器光强为

Sd=P0{1+cos[ΦS+Φm(t)]}

(21)

其中，P0为光源光强，ΦS为磁光效应法拉第相应。Φm为载波信号在图1所示调制器处两束光的相位差。采用正弦波调制时，则相位差表示为

Φm(t)=2δsin(ωτ/2)sin(Ωmt)

(22)

其中，δ为相位调制深度，ω为光波角频率，τ为延迟时间，Ωm为相位调制角频率。

由式ΦS=4NVI可知，求解ΦS即可得到电流值。

4 λ/4波片误差分析与工程研制作

4.1λ/4波片误差分析

反射式光纤电流传感器中设计的λ/4延迟器所采用的设计方案是：要求λ/4波片的偏振轴与前端保偏光纤的偏振轴以一定的角度θ对准，且令两个相互垂直的偏振模式产生相位差φ，理想情况下θ=45°，φ=90°。实际应用中，制备λ/4波片不可避免地会产生一定的误差，这种误差将会对光纤电流互感器产生不利的影响。

非理想λ/4波片的琼斯矩阵可表示为

(21)

由式(20)可将输出干涉光强化简变为

(1-h)cos(φ(t-τ)-φ(t)+4F)

(22)

其中，h=1-sinφsin2θ。同理，当采用方波调制时，式(22)光强可化简为

(23)

当系统满足闭环条件时，干涉信号的交流分量等于零，即

±hsinφf±(1-h)sin(4F-φf)=0

(24)

利用小角度简化公式sinφf≈φf，sin(4F-φf)≈4F-φf，可得

(25)

由图2可以看出，λ/4波片的对轴角度和相位延迟的控制，将直接影响反射式光纤电流互感器的尺度因子。由于光纤电流互感器应用在室外，其将承受较大温度范围的变化，λ/4波片的对轴角度和相位延迟[3]将因温度的改变发生变化，影响光纤电流互感器的实际使用性能。

图2 标度因数与对轴角度和延迟量的关系Fig.2 The relationship between the phase delay and alignment with the scale factor

4.2λ/4波片的工程研制

λ/4波片的45°熔接工艺相对较为成熟，通过消光比测试仪器的监测可以得知熔接质量，简单参数的调整可以得到更优的结果。但相位延迟的控制工艺却很难实现。根据实际测试，每段光纤的拍长和长光纤给出的测试数据有所差异，而短光纤又无法测试拍长参数，导致光纤的拍长难以掌握，而确定λ/4拍长的长度更是有难度的。几微米的差异即可影响波片的性能。图3所示为理论计算的延迟量与消光比的对应关系。

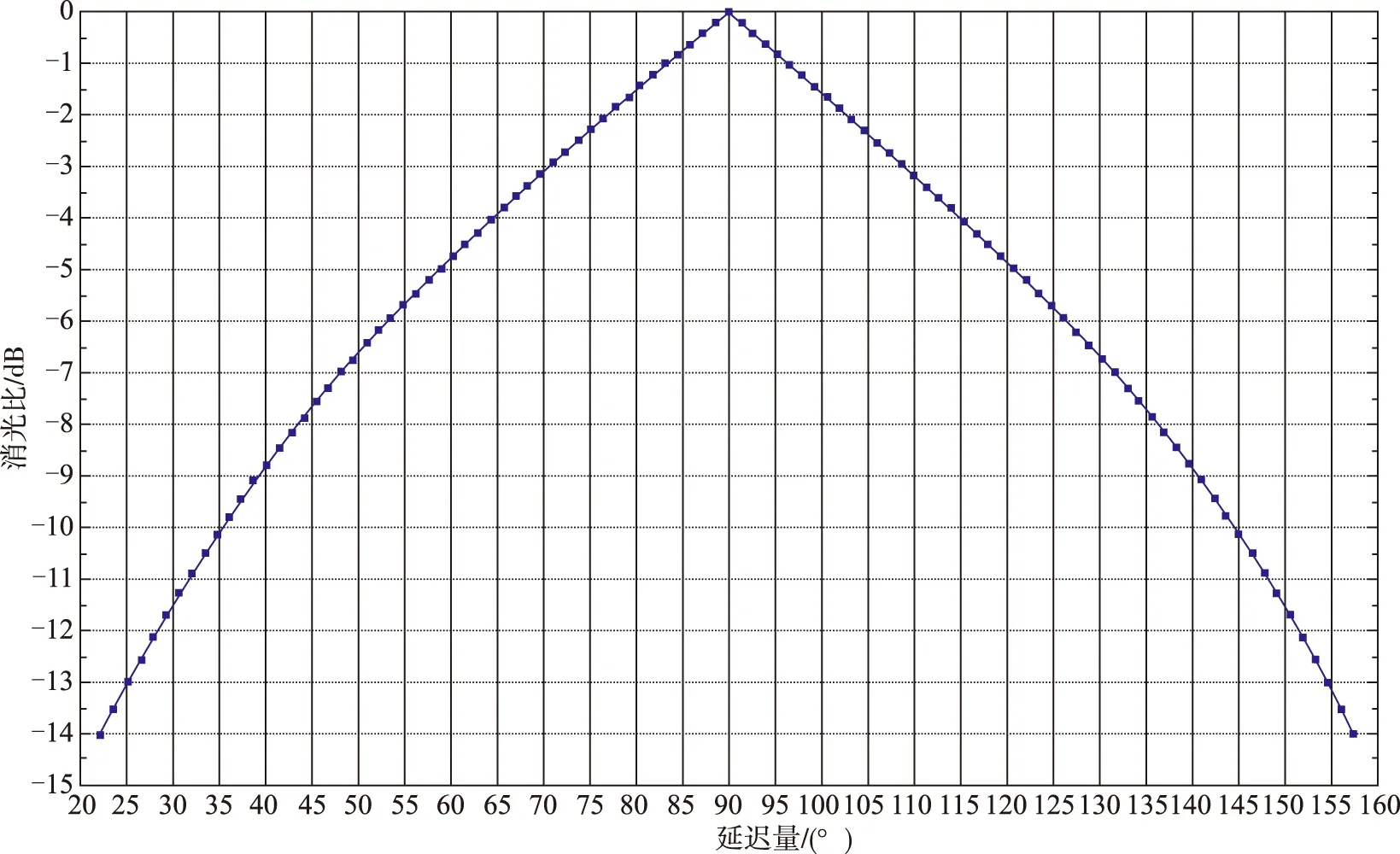
图3 延迟器相位偏差与消光比的对应关系Fig.3 The relationship between phase deviation and EX with the delayer

经过用某型光纤的多次试验，增加辅助调试工具，解决了制作的基本问题。而与理论计算的相互验证，终于得到了较优的结果。图4为理论值与实测值数据比对图(纵坐标代表消光比)。由于理论值的拍长为通过测试得到的通用拍长，因此不能真实表达实际每段光纤的拍长值，有微小的差别，但整体趋势具有一致性。印证了理论与实际的正确性。且通过试验和改进，最终可得到消光比<0.1dB的λ/4波片。

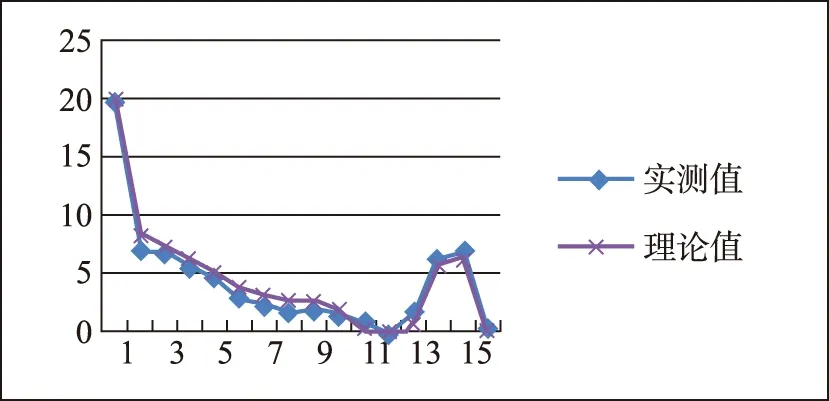
图4 延迟器消光比理论值与实际值数据对比图Fig.4 Comparison of theoretical value and actual value of the delay EX

5 结论

本文通过琼斯矩阵分析法建立了反射式光纤电流互感器的光路偏振模型，在此基础上分析了数字闭环光纤电流互感器λ/4波片的对轴角度和相位延迟量与标度因数之间的量化关系，为研究反射式光纤电流互感器的误差补偿技术提供了理论支持。通过实践，研制出了较优性能的1/4波片，为其应用做了有利支撑。

[1] 郝金会.Sagnac式光纤电流互感器研究[D].哈尔滨工程大学，2012.

[2] 廖延彪.光纤光学[M].清华大学出版社，2000.

[3] 王立辉，何周，刘锡祥，闫捷，李佩娟.反射式光纤电流互感器光波偏振态相互转换过程中的误差特效[J].电工技术学报，2013.

[4] Watekar P R，Ju S，Kim S A，et al.Development of a highly sensitive compact sized optical fiber current sensor.Optics Express，2010.

[5] Tang Mingjie，Cao Jianan.Study on magneto-optic balance type of optical fiber current transformer used in extra-high voltage measurement.2011 Third International Conference on Measuring Technology and Mechatronics Automation，2011.

Error Analysis of Quarter-waveplate for Fiber Optical Current Transducer

HUI Fei，CUI Jing，ZUO Wen-long，ZHANG Shu-ying

(Tianjin Navigation Instrument Research Institute，Tianjin 300131，China)

The phase delay and fusion alignment error of fiber optical quarter waveplate are the main reasons that makes the fiber optic current transducer(FOCT)instability.Based on the in-line Sagnac interferometer setup，we analyzed and established the Jones matrix model of FOCT in this paper.The relationship between the phase delay and alignment error with the scale factor of FOCT was linked，which makes further error compensation available.And through experimental practice，the extinction ratio that is less than 0.2dB is developed.

Quarter-waveplate；Phase delay；FOCT

2015-03-30；

2015-05-04。

“十二五”船舶预研支撑技术项目-三轴光纤陀螺及系统技术研究(62101050801)

惠菲(1985-)，女，工程师。从事舰船导航研究。E-mail：hf58665895@163.com

U666.1

A

2095-8110(2016)01-0064-05