攻击角度约束下打击机动目标的制导律

王 健，崔文昊, 史 震，池晓辉

(哈尔滨工程大学自动化学院,哈尔滨 150001)

攻击角度约束下打击机动目标的制导律

王 健，崔文昊, 史 震，池晓辉

(哈尔滨工程大学自动化学院,哈尔滨 150001)

针对某些导弹要求限制末端攻击角度的作战要求，基于滑模变结构控制理论，面向机动目标，设计了一种同时满足脱靶量和攻击角度约束要求的制导律。采用自适应滑模趋近律，并将目标机动视为干扰,利用线性变结构制导律推导出目标加速度的估计方程，并通过仿真证实了其有效性。所设计的制导律形式简单、实用。仿真结果表明，该制导律能够以期望的攻击角度命中目标，并对所提出制导律的性能进行了分析，具有一定的工程应用价值。

末端攻击角度约束；变结构控制；目标加速度的估计方程；脱靶量；制导律

0 引言

在实际应用中，一些精确制导武器(如动能拦截器、反坦克导弹、反舰导弹、鱼雷等)对目标的攻击，为了提高命中效率和毁伤效果，往往对拦截时刻导弹的攻击角度有一定的要求。

自从Kim和Grider首次在机动弹头再入制导的研究中引入落角约束问题以来[1]，一些学者根据不同的应用背景，不同的理论方法提出多种具有终端角度约束的导引律。文献[2]假定中制导与末制导衔接很好，考虑自寻的导引头框架角的限制，设计了平面内末制导阶段的最优制导律，在所需控制能量最小的前提下可以实现攻击角度的约束；文献[3]设计了带终端角度约束的变结构制导律，在目标不机动和随机机动的情况下都能满足攻击角度的要求，并给出了制导律的收敛性证明。在最新的研究中，开始研究约束目标攻击角度的三维制导律，以及考虑导弹的动态特性和有限时间收敛下的制导律。

本文基于变结构控制理论，设计了攻击角度约束下打击机动目标的变结构制导律，并用线性变结构制导律推导出了目标加速度的估计方程，并证实了其有效性。

1 末端拦截问题的数学描述和攻击角度约束下制导律设计

图1中，M、T分别代表导弹和目标，二维平面内导弹-目标的相对运动学方程为：

(1)

(2)

(3)

(4)

式中：

Vm、Vt——导弹、目标的速度，为常数；

Am、At——导弹、目标的法向加速度，垂直于各自的速度方向；

θm、θt——导弹、目标的速度方向与X轴夹角，逆时针为正；

R、q——导弹-目标的相对距离、视线角。

图1 平面内导弹-目标的相对运动关系Fig.1 Planar interception geometry

攻击角度表示为导弹拦截过程中结束时刻导弹速度矢量和目标速度矢量之间的夹角。定义tf为制导结束时刻，导弹期望的攻击角度设为Θ，攻击角度约束的制导问题是指在制导结束时刻，导弹保证零脱靶量的同时能以期望的攻击角度击中目标，即满足：

(5)

θm(tf)-θt(tf)=Θ

(6)

(7)

式(7)代表导弹击中目标在视场范围内，同时还可以得到

Vtsin(θt(tf)-qd)-Vmsin(θm(tf)-qd)=0

(8)

对于具体攻击任务的导弹，期望的攻击角度Θ是定值，如果目标运动的速度倾角θt(tf)已知时，则由式(6)可知导弹在制导结束时刻的弹道倾角θm(tf)也可以确定，也就是期望的导弹倾角θd。再由式(7)和式(8)可以得到期望终端视线角qd的值。则对于攻击角度的约束，即求解导弹的弹道倾角满足θm(t)=θd的问题，可以转化成终端视线角满足q(t)=qd的问题，这也为后面滑模面的选取奠定了基础。

目标做固定加速度或者随机加速度的机动运动时，主要讨论下面三种特殊情况，其他的攻击角度需要综合式(5)～式(8)分析得出，工程应用也比较少。

1)当垂直攻击时

θd=θt(tf)+Θ

(9)

Θ=±π/2

(10)

(11)

2)当迎面攻击时

θd-θt(tf)=-π

(12)

qd(t)=θt(tf)-π

(13)

3)当追尾攻击时

θd-θt(tf)=0

(14)

qd=θt(tf)

(15)

(16)

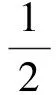
为保证系统状态能够到达滑模，且到滑模的过程中有优良的动态特性，构造自适应趋近律为

(17)

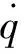
对式(16)求导，可得

(18)

将式(17)代入式(18)左端，式(3)、式(4)代入式(18)右端，可以得到变结构制导律为

(19)

(20)

于是得到非线性变结构制导律的表达式。它需要的变量多，且需要实时估计目标的加速度和速度等信息，这给它的实现带来一定难度。

2 目标加速度的估计

我们用小角度摄动法来线性化导弹-目标相对运动学方程[7-8]，最终可以得到

(21)

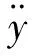
(22)

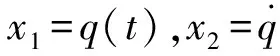
(23)

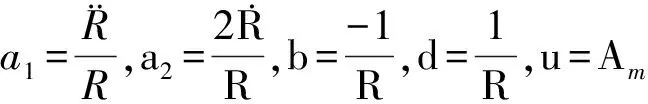
基于线性化的导弹-目标相对运动学方程式(23)，我们来推导线性变结构制导律。

滑动模态和趋近律方程与非线性变结构制导律采用的模型相同，分别为式(16)和式(17)。

(24)

在实际中，干扰f可能无法得到，式(24)可写为

(25)

(26)

于是制导律可以表示为

(27)

与非线性变结构制导律比较，线性变结构制导律不需要计算三角函数，所需运算量小；它的实现只需要获得相对速度和视线角速率2个变量，所需的变量数目小于非线性变结构制导律；只需要知道目标加速度上界，不需要对目标加速度进行估计。可见，线性变结构制导律的实现难度远小于非线性变结构制导律，由于q很小，得到

(28)

将式(28)代入式(25)，得到

(29)

式(29)与式(27)完全相同。可见，线性变结构制导律获得的导弹的指令值可以近似看作是对目标加速度的估计值。

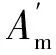
(30)

从式(30)和式(29)可以看出线性变结构制导律的工作特点。导弹在飞向目标的过程中，可以近似这样认为，实时估计目标的加速度，而且将其近似看作导弹的制导指令，引导导弹做与目标相同形式的机动，从而保证视线角速率在拦截过程中为零。

3 仿真实例

仿真情形1：对机动目标垂直攻击的情况

对机动目标垂直攻击的仿真结果如图2～图3。

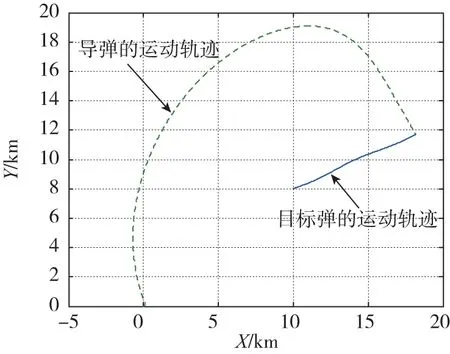
图2 导弹和目标的运动轨迹Fig.2 Trajectories of missile and target

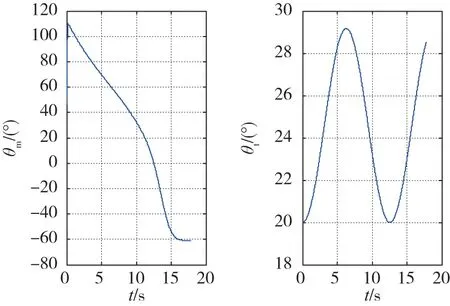
图3 导弹和目标的弹道倾角Fig.3 Trajectory oblique angles of missile and target

当目标具有正弦机动的加速度，由仿真结果可知导弹仍能在脱靶量误差允许的情况下命中目标，脱靶量为2.3562m。由已知条件可以得到制导末端结束时目标的弹道倾角近似为28.75°，已知导弹、目标速度的大小Vm、Vt和目标的弹道倾角θt的值，根据式(11)，可以得到期望的视线角qd=-75.29°，进而可以得到相应的变结构制导律，而命中目标时导弹的弹道倾角为 -60.62°，根据终端攻击角度的定义，此时攻击角度Θ=-89.37°，可以认为导弹以垂直的攻击形式命中目标。

仿真情形2：对机动目标尾追攻击的情况

对机动目标尾追攻击的仿真结果如图4～图5。

图4 导弹和目标的运动轨迹Fig.4 Trajectories of missile and target

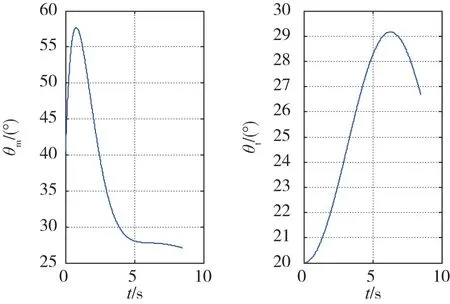
图5 导弹和目标的弹道倾角Fig.5 Trajectory oblique angles of missile and target

当目标具有正弦机动的加速度，由仿真结果可知导弹仍能在脱靶量误差允许的情况下命中目标，脱靶量为1.7852m。由已知条件可以得到制导末端结束时目标的弹道倾角近似为26.31°，已知目标的弹道倾角θt，根据式(15)，可以得到期望的视线角qd=θt=26.31°，进而得到相应的变结构制导律，而制导结束时刻导弹的弹道倾角为 27.27°，根据终端攻击角度的定义，此时攻击角度Θ=0.96°，可以认为导弹以追尾攻击的形式命中目标。

图6 导弹和目标的运动轨迹Fig.6 Trajectories of missile and target

图7 目标加速度的实际和估计曲线Fig.7 Actual and estimated curves of target’s acceleration

如图7所示，用线性变结构制导律方法对目标的加速度值进行了估计，虽然和实际值有所差异，但是可以近似认为是目标机动的加速度值，应用到非线性变结构制导律标的法向加速度中，同时变结构制导律本身具有较强的鲁棒性，仿真结果如图6所示，导弹仍能命中目标，脱靶量为1.5338m,在误差允许的范围内,证实了算法的有效性。

4 结论

本文基于变结构理论，通过对建立的导弹末制导的二维数学模型进行分析，设计了攻击角度约束下打击机动目标的制导律，所设计的制导律能够以期望的攻击角度击中目标，对机动目标有较强的鲁棒性。由于设计的制导律还依赖目标的加速度，本文应用线性化后的变结构制导律对目标的加速度进行了估计，并通过仿真证实了算法的可行性。所设计的制导律具有所需参量易于获取、制导精度高、鲁棒性强等优点，因此便于在工程中推广应用。

[1] Kim M, Grider K V. Terminal guidance for impact attitude angle constrained flight trajectories [J]. IEEE Transaction on Aerospace and Electronic System, 1973, 9 (6): 852-859.

[2] Song T L, Shin S J, Cho H. Impact angle control for planar engagements [J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35 (4): 1439-1444.

[3] Kim B S, Lee J G. Homing guidance with terminal angular constraint against non-maneuvering and maneuvering target [J]. AIAA-97-3474(S0731-5090): 189-199.

[4] Zhou D, Mu C, Ling Q, et al. Optimal sliding-mode guidance of a homing-missile [C]. Proceedings of IEEE Conference on Decision and Control, 1999: 5131-5136.

[5] Zhou D, Mu C, Xu W. Adaptive sliding-mode guidance of a homing missile [J]. Journal of Guidance, Control and Dynamics, 1999, 22 (4): 589-594.

[6] 王华吉，简金蕾，雷虎民，等. 拦截机动目标的模糊变结构导引律 [J]. 电光与控制，2014, 21 (10): 42-46.

[7] 周荻.寻的导弹新型导引规律 [M]. 北京：国防工业出版社,2002: 8-26.

[8] 高为炳.变结构控制理论基础 [M]. 北京：中国科学技术出版社,1990.

Guidance Law with Attack Angle Constraints for Maneuvering Targets

WANG Jian, CUI Wen-hao, SHI Zhen, CHI Xiao-hui

(College of Automation, Harbin Engineering University, Harbin 150001, China)

Some missiles with terminal attack angle constraints were required in the war, a guidance law based on the sliding mode variable structure control theory with miss distance and attack angle constraints was proposed for maneuvering targets. The target maneuvering was taken as a disturbance and an adaptive sliding mode approaching law was adopted, what’s more, the estimated equation of the target acceleration is deduced based on the linear variable structure guidance law，the simulation result demonstrates the estimated value. The obtained guidance law was simple and practical. The simulation shows that the guidance law can be used to ensure the missiles hit the maneuvering targets with the desirable attack angle, and the performances of the proposed guidance law were analyzed, the research can offer some references for engineering application.

Terminal attack angle constraints; Variable structure control; Estimated equation of the target acceleration；Miss distance; Guidance law

10.19306/j.cnki.2095-8110.2016.05.010

2015-04-21；

2015-07-09。

王健(1988-)，男，硕士，研究方向为导弹的制导与控制。E-mail:wangjian411@hrbeu.edu.cn

TJ765.3

A

2095-8110(2016)05-0051-05