基于FLAC3D的土工格室挡墙工程性状及敏感性因素分析

刘　军，贾喜军

(河南高速公路驻信段改扩建工程有限公司, 河南 郑州 450015)



基于FLAC3D的土工格室挡墙工程性状及敏感性因素分析

刘军，贾喜军

(河南高速公路驻信段改扩建工程有限公司, 河南 郑州 450015)

摘要：以驻信高速路基边坡的土工格室柔性挡墙工程为背景，研究土工格室挡墙的工程性状和敏感性因素。通过FLAC3D有限差分软件，模拟格室单元与填土的相互作用，对挡墙的受力与变形规律进行研究，并结合实体工程进行对比验证。同时，基于FLAC3D强度折减法，对挡墙稳定性影响因素进行了敏感性分析。结果表明：土工格室挡墙在上覆荷载作用下，墙背应力沿墙背先增大，再减小，再增大的波动形分布，并且由墙背至墙身递减；挡墙位移曲线的斜率随墙高递减，呈“网兜”状；数值计算与现场测试得到的曲线变化规律一致，表明采用的数值模型是合理的；此外，计算表明土工格室挡墙稳定性对填土内摩擦角最为敏感。研究成果对土工格室挡墙的设计与施工具有重要的参考价值和指导意义。

关键词：土工格室挡墙；FLAC3D软件；工程性状；现场测试；敏感性因素

土工格室是由高分子聚合物HDPE片材通过高强焊接而成的一种三维网状结构，因其具有良好的适应性、经济性、稳定性和生态环保等优点，广泛应用于水利、公路、铁路等领域，但其理论研究远远落后于工程实践[1-3]。目前，针对土工格室的研究主要集中在土工格室水平铺设加固地基、路堤边坡防护等方面[4-7]，少数学者对土工格室作为生态材料用于挡土墙也进行了研究，取得了一些成果。屈战辉[8]运用ANSYS软件对土工格室挡墙的工程性状进行了弹塑性仿真分析。宋飞等[9]运用Plaxis软件研究了在不同高宽比、坡度及路基表面荷载对土工格室挡墙变性性状的影响。王根等[10]以瑞鹰高速土工格室柔性挡墙工程为背景，采用ADINA有限元数值仿真分析，考虑墙体与路基土的耦合关系，研究了土工格室多级柔性挡墙的受力机理，对比多级挡墙在多种工况下的受力情况。但土工格室挡墙工程性状的研究仍不完善，缺乏系统的现场实测数据支撑。针对土工格室挡土墙稳定性敏感因素的研究更为少见，仅有的研究主要集中在挡墙的尺寸、坡度等对挡土墙受力和变形的影响，土工格室挡墙稳定性敏感性因素的影响鲜有提及，因此需要进行深入研究。

本文以驻马店至信阳(豫鄂省界)高速公路K126+880—K126+920路段作为依托，采用岩土工程有限元分析软件FLAC3D计算分析了土工格室柔性挡墙的受力与变形特征，并与实测数据对比验证了数值模拟的合理性。在此基础上研究了土工格室单元尺寸、挡墙高宽比、平均坡比、填土重度、黏聚力、内摩擦角对土工格室挡墙稳定性的影响，并据此找出敏感因素。对工程设计具有一定的参考意义。

1工程概况

土工格室生态挡墙是加筋土技术的最新发展，与传统的支挡构造物相比，具有强度高、圬工量少、外形美观、生态性能好等优点[11]。为了减少土地占用、节约工程造价并营造生态环保的公路环境，驻信高速公路K126+880—K126+920路段采用土工格室生态挡墙支挡方案。图1为断面示意图，挡墙基础埋深0.4 m，基础上部为2.6 m高墙体，墙身由13层土工格室平铺连接而成，每层格室高20 cm，每2层格室外侧连接40 cm高挡板，挡墙总高1 m。顶部为路面结构层，高1 m。为了研究土工格室生态挡墙的受力与变形特性，指导工程施工，本文以这一土工格室挡墙为例进行数值仿真分析。

图1土工格室生态挡墙示意图

2土工格室挡墙FLAC3D模型建立与参数选取

本文以美国Itasca公司的有限差分软件FLAC3D为仿真分析软件，根据图1建立仿真分析模型[12]。由于FLAC3D没有专门模拟土工格室的单元，而土工格栅性能与格室十分类似，格室可以近似看作由二维格栅竖向拉伸而成，因此，计算时土工格室采用FLAC3D自带的Geogrid单元横向和纵向布设模拟[13]，这种单元通过弹簧-滑块系统模拟筋土间的摩擦特性，筋材特性参数见表1。基础、格室内填土、路基填土和路面结构层均采用Mohr-Coulomb模型，参数见表2。模型在土工格室结构层之间、格室与填土和基础与填土的交界面上设置了接触面单元，以模拟格室层之间、格室与填土、基础与填土的相互作用[14]，网格划分详见图2。本文计算了在天然状态下土工格室挡墙墙身和墙背的受力与变形性能。

表1　筋材及筋土界面的力学参数

表2　岩土体的力学参数

图2网格划分示意图

3工程性状数值模拟

为了研究墙体所受应力和变形规律，共布设39个监测点记录挡墙所受应力和变形，监测点布设见图3。

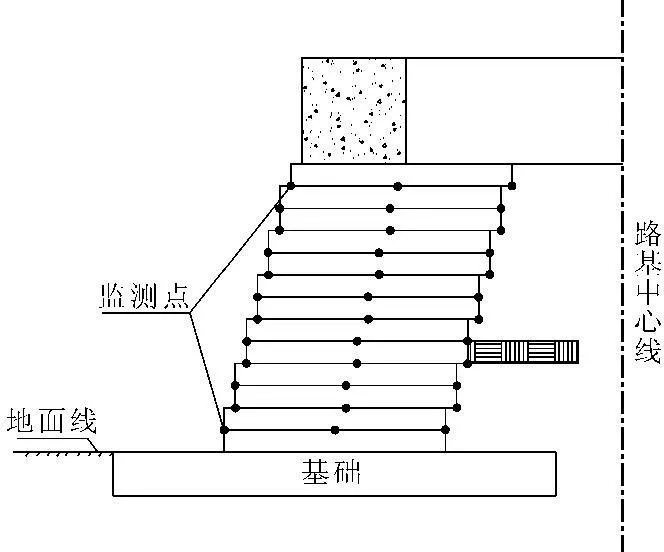
图3监测点布设示意图

图4为挡墙稳定后水平应力云图，图5为水平位移云图，由图4、图5可知，土工格室挡墙受力形式与无加筋边坡受力形式类似，土工格室生态挡墙与边坡融为一体，可以将挡墙视为加固后的边坡。

图4水平应力云图

图6为土工格室挡墙墙身和墙背受力曲线，图6显示，挡墙监测面上所受主动土压力沿墙顶至墙脚呈先增大后减小再增大分布。以墙背为例，墙顶以下0～0.4 m土压力由3.3 kPa逐渐增大至4.6 kPa，0.4 m～0.8 m压力逐渐减小至3.9 kPa，0.8 m至墙底压力又逐渐回升，墙底处达5 kPa。墙背至墙面主动土压力呈递减趋势，墙底处压力分别为5 kPa、4.7 kPa、4.5 kPa。

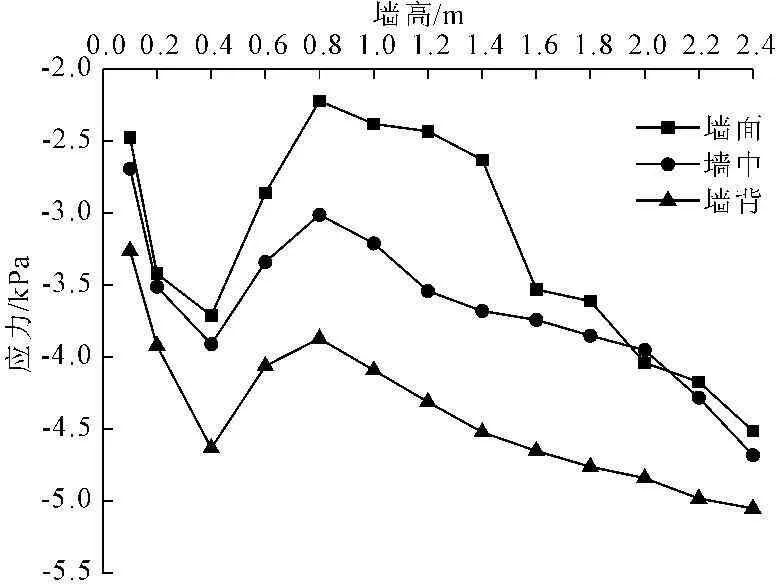
图5　水平位移云图

图6挡墙水平应力计算曲线

图7为土工格室挡墙墙身和墙背应变曲线，从图7中可以看出，从墙背至墙面变形逐渐明显，位移沿墙高呈非线性分布，表现为“网兜”形态。位移沿墙顶至墙脚先增大后减小，0～1.8 m处位移逐渐递增至1.7 cm，1.8 m至墙脚位移逐渐变小至1.1 cm。

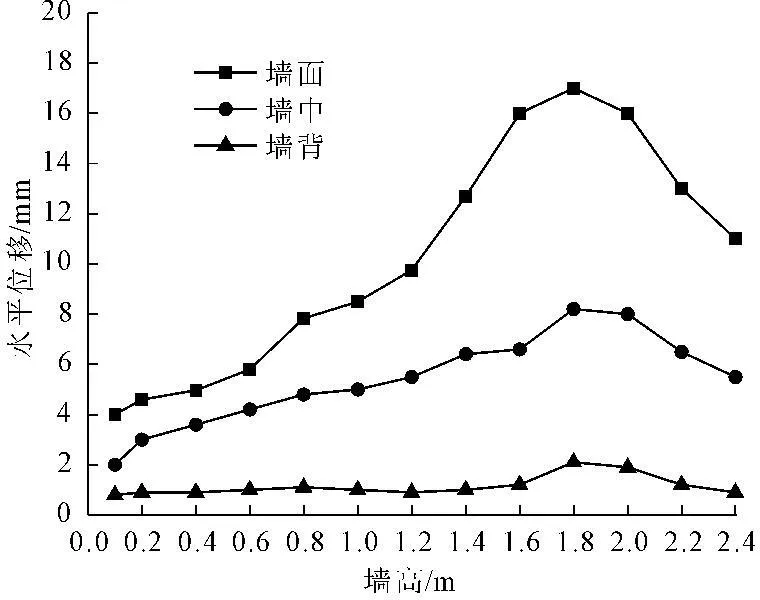
图7挡墙水平位移计算曲线

4数值模拟计算结果与现场测试结果对比

在土工格室挡墙现场施工时，在监测点位置埋设了丹东市辽丹仪表公司生产的JXY型土压力盒，施工完成150 d后观测数据。图8给出了墙体侧向土压力实测值与有限元计算值的比较曲线。实体工程中由于压力盒埋设数量有限，实测压力值无法连续反映墙身及墙背土压力变化，但从墙背与墙身实测点压力连线可看出，土压力实测曲线呈两头大，中间小的凹形分布，且反弯点出现在0.4 m处，最大值出现在墙底处，从墙背到墙面分别为4 kPa、4.3 kPa、5.6 kPa。与计算曲线比较，实测曲线也呈两头大中间小的凹形分布，曲线反弯点位置与计算曲线一致，各个测点相差均小于15%。图9为墙体变形实测值与有限元计算值的比较曲线。实体工程中由广州瑞德仪器有限公司生产的RTS-822A红外全站仪观测墙身变形，由观测曲线可以看出，挡墙变形沿墙顶往下先增大，达到一定值后减小，呈“网兜”形，最大位移出现在距墙趾0.6 m处，达15.8 mm。与计算曲线比较，实测曲线也呈同样的趋势分布，且最大值也出现在0.6 m附近，各测点实测值与计算值相差均小于20%。

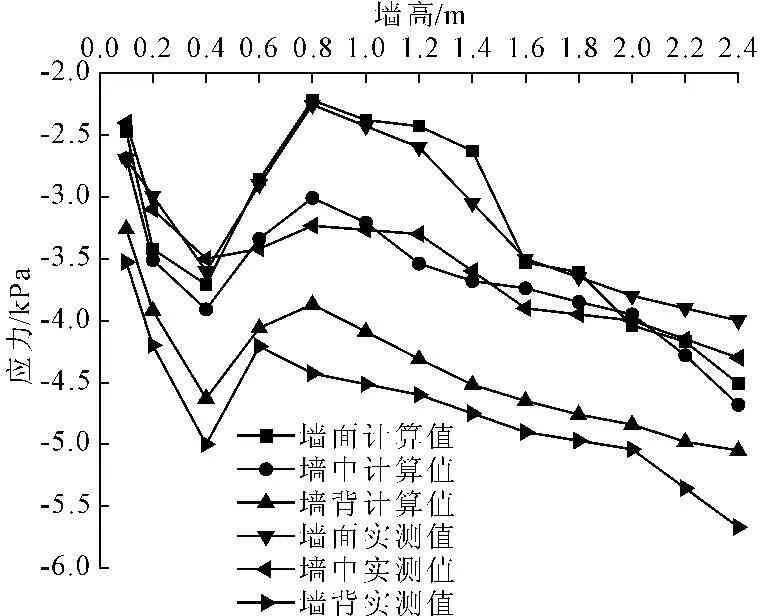
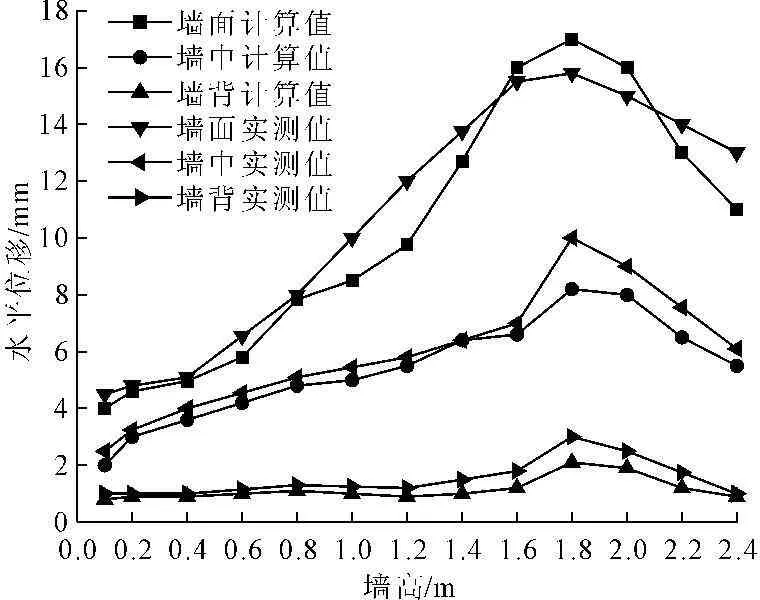
图8　挡墙应力计算值与实测值比较图

图9挡墙水平位移计算值与实测值比较图

由以上结果可知，计算结果与实测结果基本吻合，表明本文采用FLAC3D计算模型能够较好的模拟土工格室挡墙的工作性状，同时也验证了实测结果的可靠性。

5土工格室挡墙稳定性敏感因素分析

在上文研究的基础上，本文选取影响土工格室挡墙稳定性的6种因素，分别是土工格室单元尺寸、挡墙高宽比、平均坡比、填土重度、黏聚力、内摩擦角[15]，每个因素等间距取8个不同的水平，以单一因素为变量，采用FLAC3D计算确定整体稳定系数K，以稳定安全系数为指标进行多因素单指标计算分析。各因素取值见表3，稳定系数与相关参数之间的关系见图10～图16。

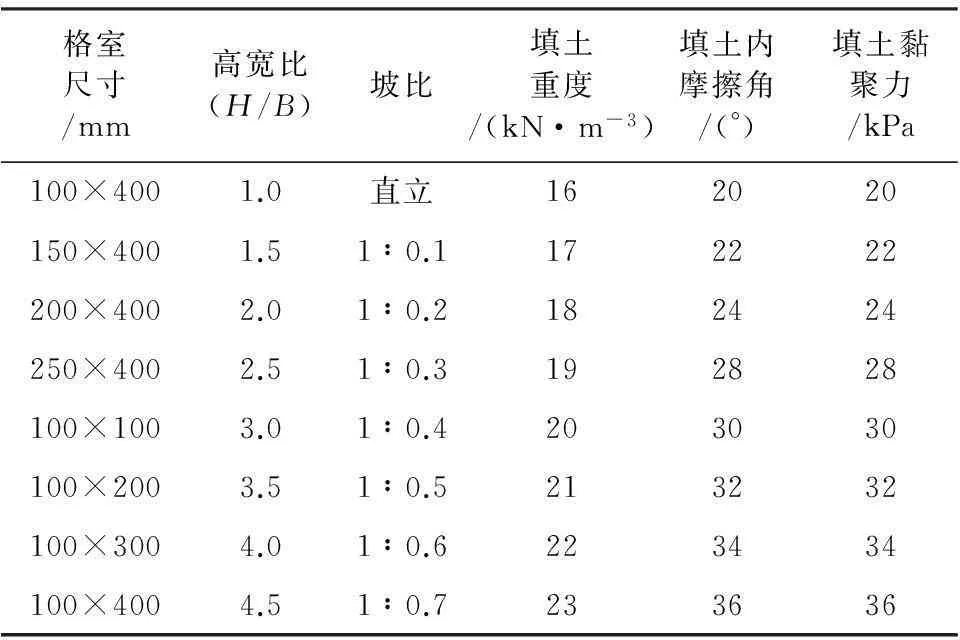
表3　稳定性影响因素表

由图10可以看出，随着格室单元高度的增加，稳定系数K值增加甚微，当高度增加1倍，即从100 mm高变化到200 mm的情况下，稳定系数K值仅增加0.05，增幅为1.3%。由图11可以看出，随着格室焊距的增大，稳定系数K值有衰减的趋势，但幅度不大，焊距从100 mm增加到400 mm时，K值减少0.08，减幅3.4%，表明格室高度和焊距对整体稳定性无显著影响。

图10K-格室单元高度关系曲线

图12显示，整体稳定系数受高宽比影响显著，随着高宽比的增大，即挡墙高度H增大，宽度B减小，稳定性近似呈线性关系，并逐渐减小。挡墙从高宽比1.0增大到4.5，K值减小0.8，减幅为37%。图13所示为坡比与稳定系数关系曲线，图13表明，坡比对稳定系数影响较小，随着坡比的减小，稳定系数K值增大趋势较缓。挡墙从直立到坡度0.7，K值仅增大0.3，增幅为13.6%。

图11　K-格室焊接间距关系曲线

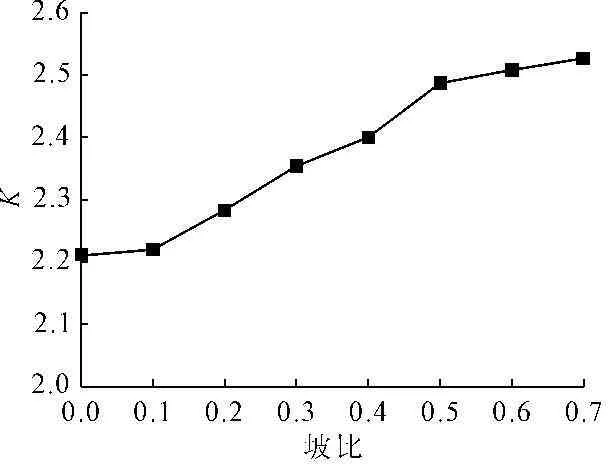
图12　K-高宽比H/B关系曲线

图13　K-坡比关系曲线

图14K-γ关系曲线

图14显示，稳定系数K受填土重度γ影响不显著，随着γ增大，K值减小幅度较小。填土γ从16 kN/m3增大到23 kN/m3，K值仅减小0.3，减幅为12.5%。图15为填土内摩擦角φ与稳定系数K值的关系曲线，图15表明，稳定系数受填土内摩擦角影响显著，即随着内摩擦角φ值的增大，稳定系数K值呈线性关系，并逐渐增大。内摩擦角从20°增加到34°，稳定系数增加0.81，增幅为74.3%。

图15K-φ关系曲线

由图16可以看出，随着黏聚力c的增大，稳定性系数K值增加甚微，近似水平。当黏聚力c值由20 kPa增加至36 kPa,稳定系数K值仅增加约0.09，增长幅度4.5%，表明其稳定性受黏聚力c值影响极小。

图16K-c关系曲线

通过对6种稳定性影响因素的敏感性分析，可得出如下结论：填土内摩擦角是影响挡墙稳定的最重要的敏感因素，随着φ值的增加，稳定性呈线性关系逐渐增大，且变化速率很快；挡墙高宽比H/B对稳定性影响也较显著，随着高宽比的增加，稳定性以较大幅度逐渐减小；挡墙坡度对稳定性也有一定影响，随着坡度的增加，稳定性以较小涨幅逐渐增大；而填土重度、黏聚力c、格室单元尺寸对稳定性敏感性均较差，影响甚微。总之，在6个影响因素中，敏感性由大到小排序为填土内摩擦角>挡墙高宽比>坡度>填土重度>填土黏聚力>格室单元尺寸。

6结论

(1) 土工格室挡墙墙背应力沿墙背先增大，再减小，再增大的波动形分布，并且由墙背至墙身递减。挡墙墙面位移曲线的斜率随墙高递减，呈“网兜”状。

(2) FLAC3D数值分析计算结果与现场实测曲线趋势一致，计算值基本等于实测值，表明本文采用FLAC3D模拟土工格室挡墙是合理的，能够较好地模拟土工格室挡墙的工作性状。

(3) 因素敏感性分析表明，土工格室挡墙稳定性对填土内摩擦角最为敏感，随内摩擦角的增加，稳定性不断增加；挡墙高宽比对稳定性影响也较大，其余依次为坡度、填土重度、填土黏聚力、格室单元尺寸。因此，在实际工程中，土工格室填料的合理选取是保证土工格室挡墙稳定性的关键。

参考文献：

[1]刘天弘.土工格室加筋挡土墙特性分析[D].大连:大连理工大学,2011:1-8.

[2]杨利.用土工格室加固的粗粒土力学特性研究[D].大连:大连理工大学,2013:1-10.

[3]宗军良.土工格室加筋路基作用机理与应用技术探讨[J].路基工程,2011(3):107-109.

[4]顾良军,余钢.土工格室加固地基的承载力探讨[J].公路交通科技,2011,28(3):6-11,35.

[5]包卫星,杨晓华,刘涛,等.清伊高速公路土工格室加固粉土地基试验研究[J].公路,2012,7(7):270-272.

[6]韩燕.土工格室防护边坡的稳定性研究[D].济南:山东大学,2012:1-8.

[7]王广月,韩燕,王杏花.降雨条件下土工格室柔性护坡的稳定性分析[J].岩土力学,2012,33(10):3020-3024.

[8]屈战辉.土工格室柔性挡墙力学性状及设计方法研究[D].西安:长安大学,2011:23-49.

[9]宋飞,许伟强,张鲁渝,等.土工格室柔性挡墙变形规律数值模拟研究[J].岩土力学,2011,32(S1):738-742.

[10]王根,杨欣,晏长根.路基柔性挡墙受力机理的有限元分析[J].福州大学学报：自然科学版,2013,41(4):609-612.

[11]陈渤,史任杰.加筋格宾和土工格室挡墙技术、经济比较[J].公路,2011(10):256-260.

[12]孙锴,彭立,杜勇立，等.基于FLAC3D煤矸石路堤沉降与应力分析与现场测试对比研究[J].公路工程,2014,39(1):83-87.

[13]杜勇立,杨果林.基于FLAC3D的加筋土挡墙施工过程仿真分析[J].工业建筑,2013,43(S1):580-584.

[14]徐健楠.柔性加筋挡墙及护坡设计方法研究[D].长沙：中南大学,2013:35-64.

[15]张家权,石维栋.土工格室柔性挡墙变形规律及破坏机理数值分析[J].公路交通科技：应用技术版,2014(4):135-138,154.

Analysis of Engineering Properties and Sensitive Factors of Geocell Flexible Retaining Wall Based on FLAC3D

LIU Jun, JIA Xijun

(HenanHighwayXinyangSectionExtensionProjectCo.,Ltd.,Zhengzhou,Henan450015,China)

Abstract：Based on the research background of geocell flexible retaining wall engineering which has been applied on Zhuxin highway subgrade slope, engineering properties and sensitive factors of geocell wall have been analyzed. By using FALC3Dfinite difference software, interaction between geocell with filling soil has been simulated to investigate the relationship between force and deformation of retaining wall. Simulation results have been compared with real world project. The sensitive factors of stability of geocell wall was also analyzed based on strength reduction method of FLAC3D. The result shows that stress curve along the back of the wall first increases, decrease later, and increasing again. The stress reduces from the back of the wall to metope. Moreover the slope of displacement curve of retaining wall reduces along the wall and the shape is like a string bag. The results from numerical simulation has the same trend with field test which means that numerical model is a promising way. Besides, the results also showed that the friction angle of filling soil is the most sensitive factor of the stability of geocell retaining wall. This research has important value to the design and construction of geocell retaining wall.

Keywords:geocell flexible retaining wall; FALC3Dsoftware; engineering properties; field test; sensitive factor

文章编号：1672—1144(2016)01—0212—06

中图分类号：TU443

文献标识码：A

作者简介：刘军(1973—)，男，河南中牟人，高级工程师，主要从事高速公路建设与管理工作。E-mail: 1026207730@qq.com

收稿日期：2015-10-01修稿日期：2015-12-30

DOI:10.3969/j.issn.1672-1144.2016.01.040