基于材料和几何非线性的张拉膜结构静力分析

张兰兰，曹　原，薛继岗

(1.江苏建筑职业技术学院 建筑工程管理学院, 江苏 徐州 221116；

2.中国矿业大学 力学与建筑工程学院， 江苏 徐州 221116)



基于材料和几何非线性的张拉膜结构静力分析

张兰兰1，曹原2，薛继岗2

(1.江苏建筑职业技术学院 建筑工程管理学院, 江苏 徐州 221116；

2.中国矿业大学 力学与建筑工程学院， 江苏 徐州 221116)

摘要：张拉膜结构作为一种新型张拉结构体系，具有明显的材料和几何双重非线性。以某张拉膜结构模型试验为例，对模型试验进行非线性有限元分析，讨论了单元类型、网格划分、材料属性等对有限元分析结果的影响，研究了张拉膜结构在静力荷载作用下的力学响应特性，研究表明：三种单元对模型试验的找形分析和荷载态分析精度比较接近，但是Shell 181则能较好的模拟材料非线性；对于低曲率膜面，几何非线性对于结构的影响要大于材料非线性的影响，可以按照材料的线弹性假定完成，对于高曲率膜面有待进一步研究；采用自由划分的网格精度可以满足低曲率膜面的精度要求，采用较密的网格化分不能有效提高结构的分析精度。

关键词：张拉膜结构；几何非线性；材料非线性；静力分析

二十世纪后期，随着材料科学、结构力学、建筑学的快速发展，以及为满足现代人对结构轻质、节能、安全、美观等追求，膜结构也应运而生了。膜结构通常由轻质高强的膜材、精细处理的钢结构支撑加上不锈钢配件组成。

较传统的建筑结构而言，膜结构的重量只有传统建筑的三十分之一，且施工方便，施工周期较短。本文研究的张拉膜结构，是利用柔性钢索作为结构骨架使膜面能够张拉形成稳定的空间曲面的膜结构形式。为保证膜面的稳定性，张拉膜结构通常采取负高斯曲面造型[1-6]。

膜结构力学性能与传统结构明显不同，具有明显的材料非线性和几何非线性。现有大多数结构分析软件用于传统刚性结构(比如钢结构、混凝土结构)时，分析精度较高，而一旦用于柔性结构时，由于存在明显几何非线性，在刚度矩阵迭代求解时，容易出现偏差，难以精确模拟柔性结构的力学性能分析[7-8]。国外在该方面的研究最为成熟和先进，开发了一系列膜结构专业分析软件主要包括两类：(1) 具有几何非线性分析的荷载分析方法的软件，比如德国的Easy软件、美国的MCM软件，日本的IMAGE软件等[8]；(2) 无荷载分析模块而单纯用于找形分析和裁剪分析的软件，比如英国的Patterner软件和Surface软件等[8]。在国内，上海同济大学、上海交通大学、北京交通大学等学校也积极编写了一批计算软件[8]。除了专业软件外，膜结构的找形和荷载分析也可以使用通用有限元软件进行分析，比如ANSYS、ABQUS、ADINA等[8-11]。由上可知，部分分析软件虽然能够考虑结构的几何非线性效应，分析时大多直接挪用板壳单元的刚度矩阵，并不能完全反映出膜材料的力学特性；另外这些软件大都基于材料的线弹性特性，无法考虑材料非线性或者只能考虑简单的弹塑性模型，不能反映出材料性能的时变性[12-13]。

本文结合已有的世博轴堆载试验数据，采用数值模拟来研究膜结构在静力荷载作用下的力学特性，最终提出一套应用简便、分析精确的膜结构数值分析方法。

1研究方案

1.1模型选取

本文的分析对象选取文献[14]中的世博轴足尺模型堆载模型试验中的单层膜模型(见图1)。试验中，首先将膜面张拉到预应力，然后再采用堆沙袋的方式施加均布荷载。沙袋铺设时，尽量做到均匀铺设于膜面上，尽量使得均匀受力。以铺设一层为一级荷载，约1 500 kg。每级荷载加完毕后静置10 min方可进行下一级的加载。每个沙袋重量为30 kg。

图1世博轴堆载试验图

1.2单元类型

ANSYS所提供的众多纷繁复杂的单元类型，对于膜结构，一般是选用Shell单元，其中应用较多的是Shell 41，Shell 63，Shell 181[15]。Shell 41是一个典型的膜单元，只具有平面内刚度，没有平面外刚度。该单元每个节点有三个平动自由度，能够考虑变厚度、应力刚化、大变形。Shell 63只支持线弹性的材料模式。Shell 63有4个节点，每个节点有3个平动自由度和3个转动自由度，一个单元共有24个自由度。Shell 181具有四节点、六自由度，能够考虑应力刚化及大变形功能。该单元有强大的非线性功能，并有截面数据定义、分析、可视化等功能。

1.3网格划分

映射网格划分是针对较规整模型的一种划分规整网格的方法，该方法的原始概念是只能对四边形面和六面体进行单元划分，且四边形面的对边上的网格划分数需保持一致，六面体的相对应的线和面上的网格划分数需保持一致，最后形成的单元也只能是四边形单元和六面体单元。该方法网格规整，计算效率高，但是划分起来比较麻烦，尤其是对于非规整结构。自由网格划分技术是一种较智能的网格划分技术，可针对不同模型自动生成合适的网格划分，结合ANSYS的智能尺寸控制技术可自动调整网格的大小及疏密分布，当然也可以通过人工控制去改变网格的大小、疏密程度以及选择分网算法。对于复杂几何模型而言，自由网格划分方法方便快捷，但往往划分生成的单元数量会很大，使得软件计算效率降低。

考虑到本次分析的模型形状是不规则的，并且为了得到更精确的模拟结果，这里我们采用了自由网格划分方式，选择了不同的网格划分密度。第一种采用人工划分，从图中可以看出模型平面被划分成三角形网格，网格划分比较均匀，一共包含1140个单元。第二种方法是软件自动控制网格的大小和疏密分布。一共将平面划分成3640个单元。第三种划分是将节点的间距缩小一半，网格更小，更密，一共将平面划分成4570个单元，相比更加均匀。

1.4材料本构关系

本次分析模型中所采用的膜材料为PTFE膜材料，属于典型的涂层织物类膜材料，具有典型的非线性、各向异性和非弹性，使膜材料拉伸性能的分析和设计增添了复杂性。因此，获得准确的膜材料的本构关系对于膜结构的找形、裁剪、施工等均至关重要。本文分析所采用的本构关系分别采用线弹性本构关系和多线性本构关系，具体数据分别来自文献[14]。

2数值模拟结果分析和讨论

2.1张拉膜结构的找形分析

张拉膜结构依靠一定的预张应力及曲面挠曲来抵抗垂直膜面的外载，其中预应力的大小和分布以及与之相应的初始平衡表面形状将决定这个结构能否承受住外载对它的作用。初始的结构形状和预应力之间是相互影响、相互制约的，这就需要通过找形分析来寻求一个合理的结构形式[16]。

膜结构形态的精度直接影响了后续的裁剪、荷载分析等分析过程，其中对裁剪的影响尤为显著。影响精度的主要因素有网格划分和更新后形态与实际工作形态的误差等[17]，为了使更新后的结构形态趋于真实平衡态，那么必须反复进行自平衡迭代；当新的不平衡矢量小于某一量值时，即可以认为结构位移已经趋于真实结果形态。和传统的找形方法相比，这种方法更结合实际。在不改变边界和输入条件以及单元网格尺寸情况下，往往自平衡迭代5次左右可以达到满意的精度。

本文选用Shell 181单元，根据前面所述的三种网格划分及本构关系分别对世博轴屋面模型进行找形分形，比较不同情况对计算的影响，见图2、图3。

通过图3对比分析这些找形分析的应力图，对于相同网格划分，各项同性和各项异性的应力图差别很大，本文前面试验研究结果表明经向试样的刚性和抗拉强度要略大于纬向试样，这充分说明了膜材料是一种各向异性材料，如果我们模拟模型所建立材料本构关系为各项同性，这与膜材料的基本力学性能不符，最后就会导致计算结果与实际值相差较大。对于不同网格划分，第三种网格划分比其他两种划分更均匀，更密集，找形分析的应力分布更精确，更接近实际应力分布图。

2.2膜结构的荷载分析

膜结构的荷载态分析是基于找形分析确定了结构预应力大小、分布及几何形态之后进行的。对张拉膜结构而言，静力分析考虑的主要是静风载、雪载、膜材自重等等。膜结构属于大变形体系，因此结构分析中必须考虑非线性因素，包括材料非线性和几何非线性[18]。对于材料的非线性，实际工程中的膜结构中应力往往处于小应力状态，因此设计和分析中往往不考虑材料的非线性，这样做可以将膜结构的分析很大程度的简化，并且计算结果与实际结果相差也不大。

用ANSYS对模型进行荷载分析，给初始形态分析后膜面施加均布荷载，得到膜结构的经向应力、纬向应力和等效应力图，见图4。

通过对比分析可以发现，膜面中部和边界应力比较大，膜材经向应力要大于纬向。对于三种不同的网格划分，应力分布也略有不同，但是从整个应力图来看，这种差别不是很大。这主要跟本模型试验的膜面曲率比较小有关系，接近平膜；但要是研究膜面局部或某些特殊位置的应力状态，显然网格划分越均匀、密集得出的结果更精确。

对张拉膜结构而言，荷载态分析考虑的主要荷载是风载、雪载、膜材自重。非线性有限单元法不仅适用于初始形态分析，而且适用于静力分析。膜结构在荷载作用下属于大变形体系，因此设计分析中必须要考虑几何非线性。关于材料非线性，从图5可以看出软件中定义的考虑了材料非线性的全新膜材模型较没有考虑材料非线性的各向异性模型得到的分析结果更加接近试验数据。一般来讲，在初步设计分析时，可以暂时不考虑，能够提高计算效率，使问题简化，但是涉及到精细分析时，需要考虑材料的非线性。另外，采用线弹性本构关系和多线性随动强化模型来模拟材料的本构关系，发现两者在本模型试验中差别不大，经分析发现，主要原因在于本模型试验中，试验模型相对简单，曲率比较平，接近于平面，在分析中，几何非线性所起的作用要大于材料非线性所起的作用，因此可以近似的采用线弹性本构关系来模拟此类简易堆载试验。

图2不同网格划分方法的找形结果分析

2.3分析小结

结合前两节的数值模拟分析，发现在张拉膜结构的有限元分析中，采用Shell 181来比较合适，能够准确地模拟张拉膜结构的几何、材料双重非线性行为。这主要是由于Shell 41具有面内刚度，不具备面外刚度，而Shell 63既具有面内刚度又有面外刚度能力，但是上述两种单元的缺点在于只能考虑弹性，不能考虑弹塑性，而Shell 181具有强大的非线性功能，能够同时考虑材料非线性和几何非线性。

对于低曲面膜面来讲，线弹性本构关系和多线性本构关系差别不大，可以采用线弹性本构关系来进行近似分析；对于低曲面膜面来讲，自由划分的网格精度可以，但是对于高曲率曲面，比如马鞍面是否适用有待于进一步研究。

由于膜结构具有高度的非线性，通过分析对比发现，网格密度越大，分析精度相对越高，另外，需要注意对单元进行检查，防止发生膜面松弛或出现褶皱。因此在荷载分析中，平衡方程不再是线性的了。膜结构荷载态分析过程中，会由于结构的刚度和强度不够，出现受压单元、单元应力超限及结构过大变形等情况。则需要采取相应措施来增加结构刚度，调整结构设计。

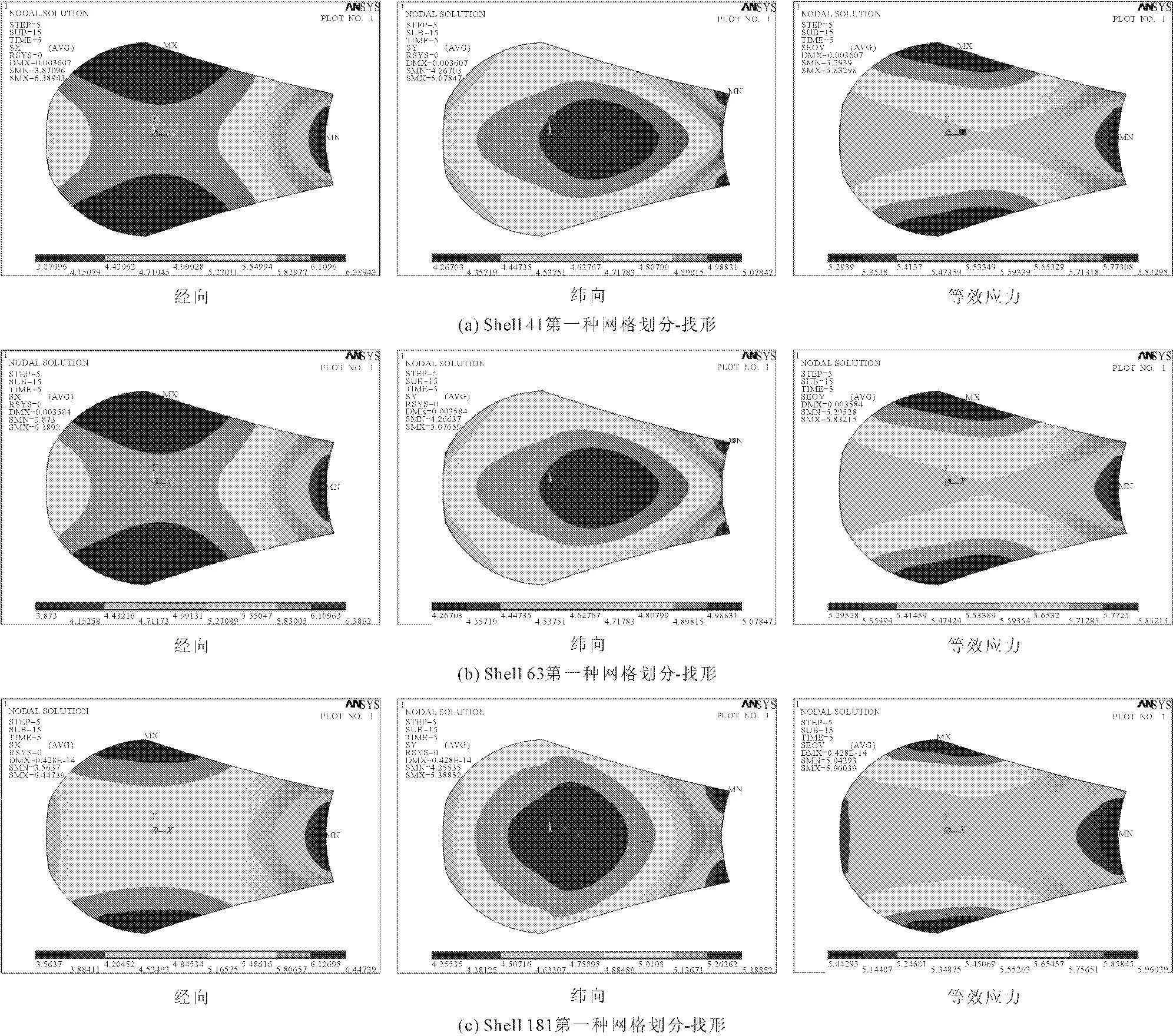
图3不同单元类型的找形图

3结论

张拉膜结构呈现出典型的材料、几何双重非线性。本文选用上海世博会世博轴足尺堆载模型试验作为分析模型，采用非线性有限元对膜结构的找形与荷载非线性分析做了全过程分析，研究了单元类型、网格划分密度、本构关系等对数值模拟结果的影响，得到了一些有效结论，能够为膜结构的静力非线性分析提供参考。

(1) 对于本模型试验的找形分析和荷载态分析，三种单元类型的分析精度比较接近，但是Shell 41比较适用于线弹性的几何分析，无法考虑材料的非线性问题，而Shell 181则能较好的模拟材料非线性。

(2) 对于低曲率膜面，几何非线性对于结构的影响要大于材料非线性的影响，可以按照材料的线弹性假定完成，对于高曲率膜面有待进一步研究。

(3) 采用自由划分的网格精度可以满足低曲率膜面的精度要求，采用较密的网格化分不能有效提高结构的分析精度。

参考文献：

[1]张其林.索和膜结构[M].上海:同济大学出版社,2002.

[2]杨庆山,姜忆南.张拉索—膜结构分析与设计[M].北京:科学出版社,2004.

图4不同单元类型和网格化分的荷载态分析图

[3]陈务军.膜结构工程设计[M].北京:中国建筑工业出版社,2005.

[4]武岳,杨庆山,沈世钊.膜结构分析理论研究现状与展望[J].工程力学,2014,31(2):1-14.

[5]武岳,伞冰冰,孙晓颖.膜结构的概念设计与形态优化[J].空间结构,2012,18(3):35-40.

[6]武岳,杨庆山,沈世钊.膜结构分析理论研究现状与展望[C]//第22届全国结构工程学术会议论文集第Ⅰ册，2013:1-14.

[7]祝效华,余志祥.ANSYS高级工程有限元分析范例精选[M].北京：电子工业出版社,2001:83-121.

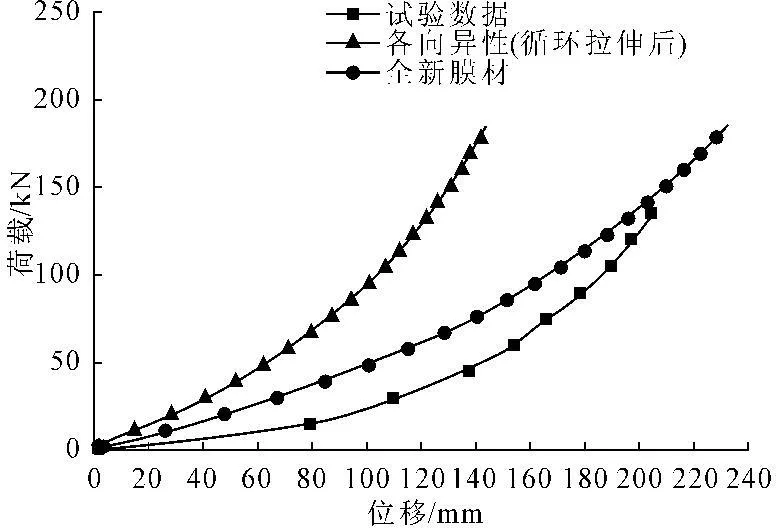
图5不同荷载本构关系下的荷载—位移曲线

[8]白建昆.索膜结构非线性有限元分析[D].重庆：重庆大学,2009.

[9]段有恒.索膜结构张拉及加载全过程仿真分析研究[D].北京：北京交通大学,2012.

[10]葛家琪，张国军，李晓通，等.索膜整体张拉结构静动力性能分析[C]//第十四届全国现代结构工程学术研讨会论文集,2014:28-33.

[11]王树,张国军,翟文博.索膜整体张拉结构成形分析[C]//第十四届全国现代结构工程学术研讨会,2014.

[12]张营营,张其林,吴明儿.膜材料性能及其对结构的影响[J].空间结构,2012,18(2):70-78.

[13]樊玉新,夏健.降落伞膜索非线性有限元模拟[J].计算力学学报,2014(6):793-798.

[14]陈鲁,汤海林,张其林，等.上海世博会世博轴膜结构屋面局部足尺试验研究[J].施工技术,2009,38(8):25-27.

[15]伞冰冰,武岳,沈世钊.膜结构有限元分析中的平面单元与曲面单元的比较[J]. 工程力学,2008,25(2)：168-173.

[16]伞冰冰,武岳,卫东,等.膜结构的多目标形态优化[J].土木工程学报,2008,41(9):1-7.

[17]李海蛟，伞冰冰，武岳.脊骨式膜结构的形态优化分析[J].空间结构，2010，16(1)：51-56.

[18]张兰兰.张拉膜结构的有限元分析[J].河南城建学院学报,2011,20(3)：27-31.

Static Analysis of Tensioned Membrane Structures Based on the Geometrical and Material Nonlinearity

ZHANG Lanlan1, CAO Yuan2, XUE Jigang2

(1.CollegeofConstructionManagement,JiangsuJianzhuInstitute,Xuzhou,Jiangsu221116,China;2.SchoolofMechanicsandCivilengineering,ChinaUniversityofMiningandTechnology,Xuzhou,Jiangsu221116,China)

Abstract：Tensioned membrane structure is a new tension system, which performs significant geometrical nonlinearity and material nonlinearity. However, the current analysis method only involves the geometrical nonlinearity, the material nonlinearity is not considered. Furthermore, lack of experience in modeling and not enough experiment results can also lead to large deviations in the analysis and potential safety hazards in the engineering. Based on the model tests of a tensioned membrane structure, the nonlinear finite element analysis was conducted to study the mechanical response of this structure under static loading. The effect of element type, meshing and material properties on the analysis results were considered. The results indicate that: according to the three element types, the accuracy of form finding analysis and loading state analysis is close, however, shell 181 can simulate material nonlinearity better; the geometric nonlinearity has a greater influence on low curvature membrane surface structure than material nonlinearity, thus, the structure can be analyzed by the linear elastic material assumptions, further study on high curvature membrane surface is needed; the free partitioning grid can meet the accuracy requirements of low curvature membrane surface, denser meshing can not effectively improve the accuracy of the structure analysis.

Keywords:tensioned membrane structure; geometrical nonlinearity; material nonlinearity; static analysis

文章编号：1672—1144(2016)01—0166—06

中图分类号：TU312+.1

文献标识码：A

作者简介：张兰兰(1984—)，女，河南商丘人，讲师，硕士，主要从事建筑工程方面的教学与研究工作。E-mail: zhanglanlan007@163.com

基金项目：江苏建筑职业技术学院校级科研项目(JYA14-09)；国家自然科学基金项目(51308532)

收稿日期：2015-08-09修稿日期：2015-09-11

DOI:10.3969/j.issn.1672-1144.2016.01.031