基于矢量和分析法的大型边坡稳定性分析研究

沈　冰，邓　琴

(1.云南省公路局, 云南 昆明 650200； 2.云南华丽高速公路建设指挥部， 云南 丽江 674100；

3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室， 湖北 武汉 430071)



基于矢量和分析法的大型边坡稳定性分析研究

沈冰1,2，邓琴3

(1.云南省公路局, 云南 昆明 650200； 2.云南华丽高速公路建设指挥部， 云南 丽江 674100；

3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室， 湖北 武汉 430071)

摘要：目前基于矢量和分析法的边坡稳定性研究还未在大型工程中得到验证，解决问题的系统性体系还未能形成。为此以金沙江大桥建设工程丽江岸边坡为研究对象，验证矢量和分析法的正确性、可靠性及分析优势。分析时考虑自然状态工况和两种不同烈度的地震工况，利用矢量和分析法初步分析确定最可能滑动模式和潜在滑移面，并计算边坡稳定性安全系数。对比分析极限平衡法、二维矢量和分析法和三维矢量和分析法的计算结果。结果表明，用二维矢量和分析法潜在滑移面的思想是可行的，且其计算结果与极限平衡法相对误差较小，而三维矢量和分析法计算精度较二维更高，对边坡滑动分析要求更高的工程中推荐应用三维矢量和分析法分析其稳定性问题。

关键词：边坡稳定；矢量和分析法；极限平衡法；潜在滑移面

现如今，边坡的稳定性定量分析法在工程中应用最为普遍的主要是刚体极限平衡分析法和强度折减分析法两种，其中刚体极限平衡法因其操作相对简单方便、理论概念比较清晰明确而被广泛认同，并且国内的相关规范也主要是基于刚体极限平衡理论分析方法进行编制[1]。从20世纪70年代以来，强度折减分析法开始提出并逐渐兴起，国内外众多学者对该方法的深入探讨和研究，极大地推动了强度折减法的发展，及其在边坡稳定性分析中的应用与研究[2-4]。强度折减分析法认为边坡在达到临界失稳状态时与之相对应的折减系数即为稳定性安全系数，其优点是无需计算之前进行条分并假定滑动面的位置。然而，由于强度折减分析法的影响因素较多，接近临界状态时，数值计算收敛相对困难且计算时间偏长，加上目前边坡失稳判据(即安全系数计算过程的终止条件)尚无统一标准，导致在实际工程应用中对于一个相同的问题，不同的研究人员可能得到的安全系数有很大差别[5]。

19世纪80年代出现了一种不采用强度储备概念来计算安全系数的极限平衡分析法，该方法不需要经过迭代计算即可计算得到作用在最后一个条块的外界面上的拉力和剩余推力。这一概念最先是由葛修润院士提出，他认为最准确的抗滑稳定安全系数概念应该是边坡在各种荷载(包括自重)的作用下，潜在滑移面上的极限抗滑力的总和与滑动力的总和之比(其中总和是指力的矢量和)。近些年来，葛修润院士和他的研究团队继续对这一分析方法展开了深入研究，并把这一新方法叫做矢量和分析法。矢量和分析法的稳定性安全系数求解公式不需要迭代计算求解，从而不存在收敛性问题，这在三维边坡稳定性问题分析上更具有优势[6-11]。

但是上述基于矢量和的边坡稳定性研究基本还未在大型工程中得到验证，解决问题的系统性体系还未能形成。本文以华坪至丽江金沙江大桥建设工程丽江岸边坡为分析对象，考虑自然状态工况和两种不同烈度的地震工况，首先利用二维矢量和分析法进行初步分析，初步确定二维边坡最可能滑动模式和潜在滑移面，并计算边坡稳定性安全系数和潜在滑移面的整体下滑方向。然后运用三维矢量和分析法对丽江岸边坡的稳定性安全系数和下滑方向进行计算，并对比分析了极限平衡法、二维矢量合法和三维矢量合法的计算结果，以验证矢量和分析法的正确性、可靠性及分析优势。

1边坡稳定性矢量和分析理论

1.1矢量和分析法安全系数计算公式

潜在滑移面所受到的总的极限抗滑力与总的滑动力分别在滑移面整体下滑趋势方向上的投影之比即为矢量和分析法的安全系数[7-9]。

(1)

(2)

图1潜在滑移面S上点A的受力示意图

τn=σs-σn

(3)

则有：

(4)

(5)

(6)

则边坡稳定性矢量和分析方法的安全系数计算公式为：

(7)

1.2矢量和分析法分析步骤

边坡抗滑稳定矢量和分析法的系统性分析步骤如下：

(1) 根据地质资料建立二维数值模型，运用二维矢量和分析法初步分析确定最可能滑动模式和潜在滑移面，并计算安全系数和下滑方向[10]。

(2) 建立三维数值模型，运用三维矢量和分析法计算安全系数和下滑方向。

(3) 根据计算结果来分析和判断边坡的稳定性情况。

(4) 利用极限平衡法计算边坡的稳定性安全系数，对比验证矢量和分析法计算结果的正确性及可靠性。

2二维矢量和分析法边坡稳定性分析

本文以华坪至丽江金沙江大桥建设工程丽江岸边坡为分析对象，丽江岸为逆向坡，2 000 m高程以下较陡，陡崖发育，存在失稳条件。

2.1计算模型和材料参数

利用大型有限元计算软件ABAQUS建立边坡二维有限元分析模型，采用Mohr-Coulomb弹塑性屈服准则，计算模型及边界条件详见图2(单位为m)。计算所用材料参数如表1所示。计算分析时考虑丽江岸边坡所受的荷载有三种工况：(1) 自然状态工况，边坡只受重力荷载作用；(2) 8级烈度地震工况，边坡受重力荷载作用和地震荷载重作用；(3) 9级烈度地震工况，边坡受重力荷载作用和地震荷载重作用[12]。

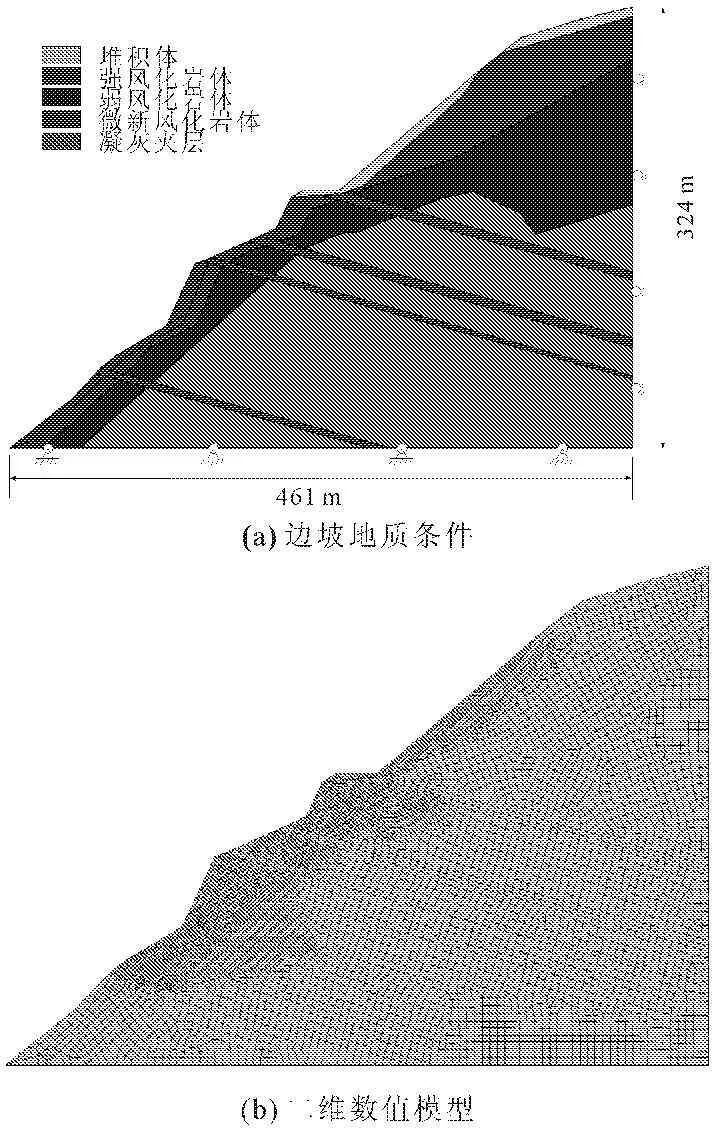
图2　边坡地质条件及二维数值模型

2.2滑移面剪出角度对边坡稳定性的影响

为研究滑移面不同剪出角度对边坡稳定性的影响，以便确定反分析中的最可能滑出角度，设计了如下计算方案：后缘结构面确定(距坡面平均距离约为20 m)，设置不同的滑移面剪出角度，分别为0°、15°、30°、45°(图3)，分析不同滑移面剪出角度下边坡稳定性的变化规律(图4)。

图3　不同剪出口角度的滑移面

图4不同剪出口角度下的边坡安全系数

可见，当滑移面剪出角度为30°时，边坡的安全系数最小，随着角度减小，边坡稳定性迅速增加，随着角度增大，边坡稳定性也有一定幅度提高。主要是由于滑移面剪出面主要由结构面和岩体组成，随着剪出角度增大，滑移面主要切穿岩体，其方向近似垂直于结构面，因此抗剪强度增大。角度减少，虽然方向接近结构面方向，但是下滑力有限，因此剪出角度过大或过小时边坡安全系数都较大。可以认为，剪出角30°是对边坡稳定性最不利的，后续的计算中主要考虑滑移面剪出角度为30°。

2.3前缘剪出面深度对边坡稳定性的影响

为研究前缘剪出面的不同深度对边坡稳定性的影响，设计了如下计算方案：后缘结构面确定(距坡面平均距离约为20 m)，设置不同高程的前缘剪出面(图5)，剪出角度为30°，分析边坡稳定性的变化规律(图6)。

分析可知，剪出面深度为30 m的滑移面安全系数最小，小于30 m的滑移面安全系数有所提高，剪出面深度大于30 m后，随着深度增加边坡的安全系数迅速逐渐增大。这表明，边坡即使失稳，也不会发生较深的滑动。

图5　不同剪出口深度的滑移面

图6不同剪出口深度条件下的边坡安全系数

2.4潜在滑移面稳定性分析

根据之前的计算结果，安全系数最小时滑移面的剪出口埋深为30 m，剪出角度为30°，为研究后缘结构面距坡面距离对边坡稳定性的影响，针对最可能的滑动模式分别选取5个最危险的潜在滑移面，陡倾结构面距坡面距离分别为16 m、30 m、50 m、80 m、120 m(图7)，分析边坡稳定性变化规律，各工况下各滑移面的安全系数及下滑方向详见表2。

图7　潜在滑移面位置示意图

由表2可知，3种工况下边坡稳定性具有相似的规律，随着后缘陡倾结构面距坡面距离增加，边坡安全系数逐渐增大，且陡倾结构面距坡面距离超过30 m后安全系数显著增大。埋深较浅的滑移面1和滑移面2不满足工程的稳定性要求，需要在施工时提供加固措施。丽江岸坡在自然条件下，各个滑移面均处于稳定状态，与实际现状相符；在8级烈度地震条件下，岸坡浅层处于临界状态；在9级烈度地震条件下，岸坡浅层处于失稳状态。

3三维矢量和分析法边坡稳定性分析

边坡三维模型的有限元网格如图8(a)所示，X方向取长度914 m，Y方向取长度374 m，Z方向沿河谷向下取663 m。各岩土层本构关系采用弹塑性模型，屈服准则采用摩尔库仑强度准则，材料参数与上节相同。边界条件为：模型中侧面为法向约束，底面为固定约束。

由于目前三维滑移面搜索的技术困难，也是目前科学研究中的工作难点。在本节中，我们采用前述二维分析搜索出来的滑移面进行空间延展，来分析边坡的三维稳定性安全系数。滑移面在边坡中的位置如图8(b)所示。由于二维计算中的滑移面1、滑移面2属于浅层滑动，在三维模型中由于地表的凹凸无法切出合适的滑体，因此三维计算中舍去这两个滑移面。这里三维滑移面1、2、3分别对应二维的滑移面3、滑移面4、滑移面5。计算结果如表3所示。从表3中可以看出，所有滑移面在3种计算工况下均满足工程稳定性。

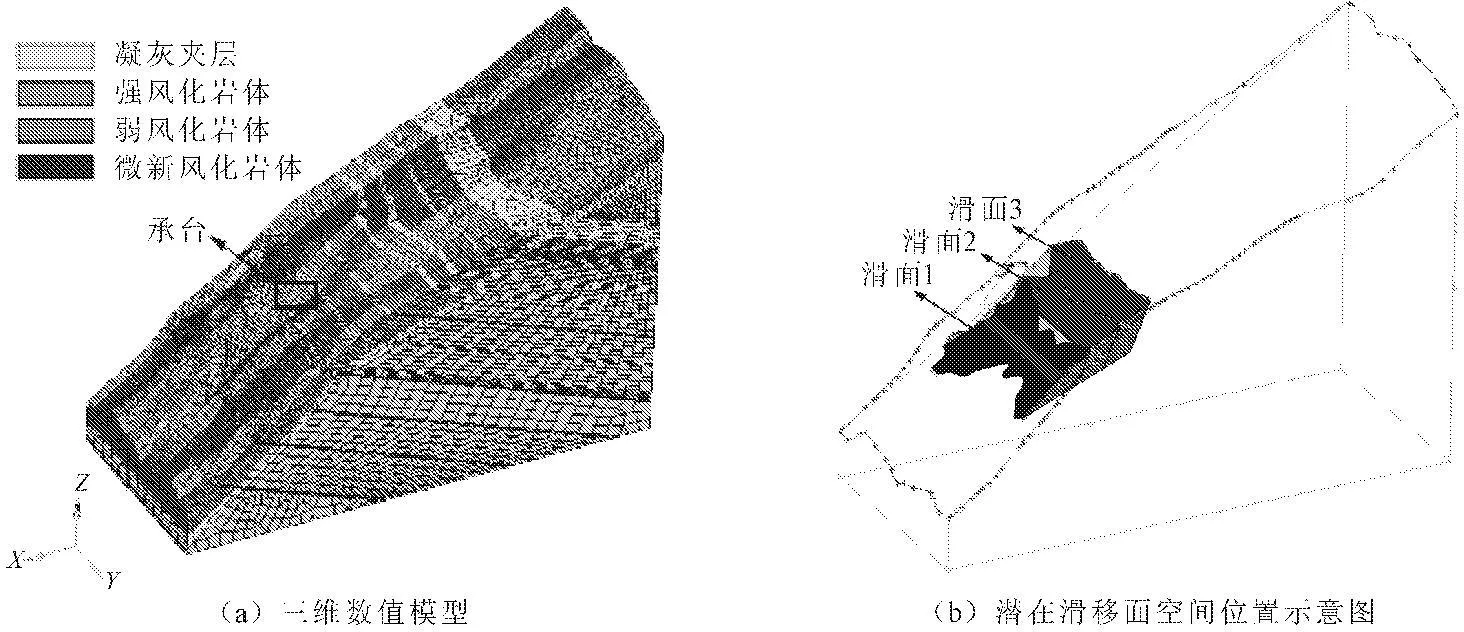
图8　三维数值模型及潜在滑移面位置

4稳定性安全系数对比分析

利用二维极限平衡法(Janbu法)对5个潜在滑移面进行计算，并将计算结果和二维、三维矢量和分析法计算结果进行比较分析，详见图9。

由图9看出，极限平衡法和二维矢量和分析法得到的边坡安全系数具有相同的规律，安全系数不超过2时，两种方法的相对误差很小，可得到相同的稳定性分析结论。边坡稳定性安全系数随滑体厚度增加而增加，滑体厚度超过30 m后其稳定性显著增加。在自然状态、8级烈度地震、9级烈度地震条件下自动搜索得到的最不利滑移面1，其稳定性(极限平衡法的安全系数分别为：1.12、0.99、0.92；二维矢量和分析法的安全系数分别为：1.09、1.01、0.89)均不满足工程稳定性要求(1.35/1.15)，但均为不超过30 m的浅层滑动，可通过工程措施加固处理。

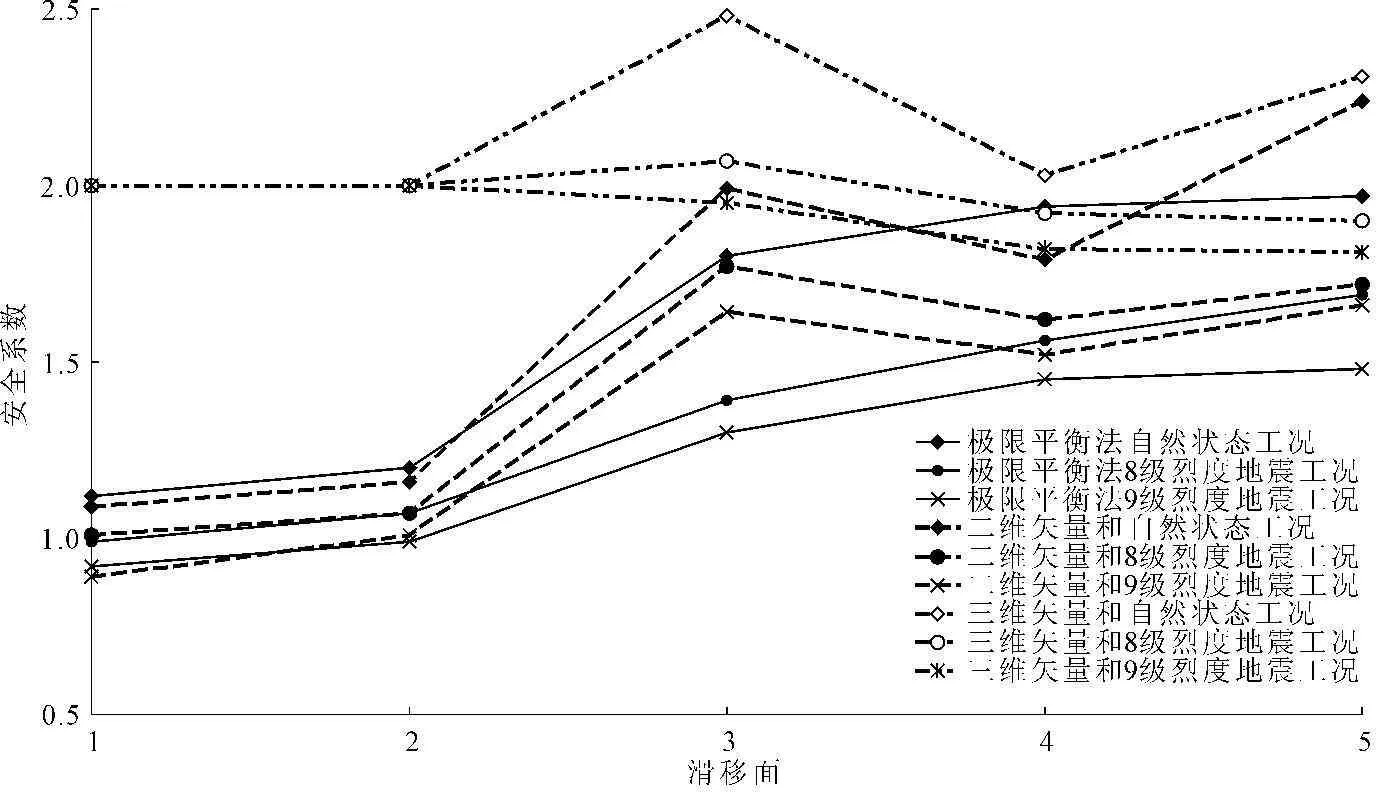
图9不同分析方法各工况稳定性安全系数

边坡的三维计算分析与二维计算分析规律基本一致，从计算结果的对比看，三维计算得到的边坡安全系数较二维计算结果有所提高。三维安全系数较二维安全系数不同主要基于以下两个原因：一是三维边坡的端部效应令边坡安全系数增大；二是三维计算可得到最不利的下滑方向，导致边坡的安全系数减小。这两者的叠加最终令安全系数增大，表明边坡端部效应对边坡稳定性的影响大于后者。

5结论

通过对丽江岸边坡的稳定性问题进行系统性的矢量和分析法分析，得出以下结论：

(1) 采用二维矢量和分析法得到不同滑动范围的边坡安全系数，并搜索最小安全系数的滑动面，通过对滑移面优化，得到最危险滑移面并进行稳定性分析，这种搜索潜在滑动面的思想是可行的。

(2) 极限平衡法和二维矢量和分析法得到的边坡安全系数具有相同的规律，两种方法计算得到的安全系数相对误差很小，可得到相同的稳定性分析结论；同时该方法不用事先假定滑移面且无需迭代求解，不存在收敛性问题，表明矢量和分析法比极限平衡法在解决大型边坡工程的稳定性分析问题方面更加可靠。

(3) 边坡的三维计算分析与二维计算分析规律基本一致，但边坡安全系数有一定的出入，这是由于三维计算可以考虑边坡的端部效应和最不利下滑方向，理论上三维矢量和分析法计算精度较二维更高。然而，三维矢量和分析法在大型工程中的应用还需要进一步的检验和验证。

致谢

感谢云交科2014(A)01—《金沙江中游库区高速公路大跨径桥址高边坡灾害调控技术及应用示范研究》项目的资助及课题组全体人员的配合、帮助和支持。

参考文献：

[1]夏元友，李梅.边坡稳定性评价方法研究及发展趋势[J].岩石力学与工程学报，2002，21(7):1087-1091.

[2]Duncan J M. State of the art: limit equilibrium and finite element analysis of slopes[J]. Journal Geotechnical Engineering, 1996,122(7):577-596.

[3]Griffiths D V, Lane P A. Slope stability analysis by finite elements[J]. Geotechnique, 1999,49(3):387-403.

[4]赵尚毅,郑颖人,时卫民,等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.

[5]陈力华,靳晓光.有限元强度折减法中边坡三种失效判据的适用性研究[J].土木工程学报,2012,45(9):136-146.

[6]葛修润.用PC型微机对岩体工程课题进行有限元分析[C]//第一届全国计算岩土力学研讨会论文集.成都:西南交通大学出版社,1987:74-85.

[7]葛修润.抗滑稳定分析新方法——矢量和分析法的基本原理及其应用[C]//岩石力学与工程的创新和实践：第十一次全国岩石力学与工程学术大会论文集.武汉：湖北科学技术出版社，2010:26-44.

[8]葛修润.岩石疲劳破坏的变形控制律、岩土力学试验的实时X射线CT扫描和边坡坝基抗滑稳定分析的新方法[J].岩土工程学报,2008,30(1):1-20.

[9]郭明伟,葛修润,李春光,等.基于矢量和方法的边坡稳定性分析中整体下滑趋势方向的探讨[J].岩土工程学报,2009,31(4):577-583.

[10]杨超，董立山，申俊敏，等.边坡矢量和分析法最危险滑面搜索研究[J].安全与环境工程,2014,21(3):28-35.

[11]刘艳章,葛修润,李春光,等.基于矢量法安全系数的边坡与坝基稳定分析[J].岩石力学与工程学报,2007,26(10):2130-2140.

[12]郭明伟,葛修润,王水林,等.基于矢量和方法的边坡动力稳定性分析[J].岩石力学与工程学报,2011,30(3):572-579.

Analysis of the Stability of Large-scale Slope Based on Vector Sum Method

SHEN Bing1,2， DENG Qin3

(1.YunNanHighwayBureau,Kunming,Yunnan650200,China； 2.YunnanHualihighwayconstructionheadquarters,Lijiang,Yunnan674100,China； 3.StateKeyLaboratoryofGeomechanicsandGeotechnicalEngineering,InstituteofRockandSoilMechanics,ChineseAcademyofSciences,Wuhan,Hubei430071,China)

Abstract：The analysis of slope stability has not been verified in large-scale project based on vector sum method, and the whole system for this issue has not appeared yet. Therefore this paper took the Lijiang slope of Jinsha River bridge construction project as an example to prove the effectiveness, reliability and advantages of vector sum method. Firstly, the most possible sliding mode and latent slide plane were analyzed and determined preliminarily by vector sum method considering the nature case and two different earthquake intensities. Meanwhile, the safety factors were calculated and the computation results of limit equilibrium method and 2D and 3D vector sum method were compared which demonstrated that the idea about analysis of latent slide plane by vector sum method was feasible, and the safety factors by the former were similar to that by limit equilibrium method. Besides, the computational accuracy of 3D vector sum method is better than 2D, which should be recommended in the field of large-scale slope engineering.

Keywords:slope stability; vector sum method; limit equilibrium method; latent slide plane

文章编号：1672—1144(2016)01—0118—06

中图分类号：TU45

文献标识码：A

作者简介：沈冰(1972—)，男，云南昆明人，高级工程师，主要从事高速公路设计、施工与管理工作。 E-mail: shenbing1972@163.com

基金项目：云南省交通运输厅科技项目(云交科2014(A)01)

收稿日期：2015-09-24修稿日期：2015-10-23

DOI:10.3969/j.issn.1672-1144.2016.01.022