型钢超高强混凝土框架边节点恢复力模型研究

刘　伟，贾金青，涂兵雄

(1.大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116024；

2.华侨大学 土木工程学院， 福建 厦门 361021)



型钢超高强混凝土框架边节点恢复力模型研究

刘伟1，贾金青1，涂兵雄2

(1.大连理工大学 海岸和近海工程国家重点实验室， 辽宁 大连 116024；

2.华侨大学 土木工程学院， 福建 厦门 361021)

摘要：通过对6个型钢超高强混凝土框架边节点进行低周往复试验，研究了轴压比、体积配箍率对边节点抗震性能的影响，并在试验结果的基础上，通过理论分析及回归分析建立了考虑轴压比及体积配箍率影响的恢复力模型。研究表明：轴压比与体积配箍率对型钢超高强混凝土边节点骨架曲线各特征点均有不同程度的影响，建议的恢复力模型与试验结果吻合良好，为型钢超高强混凝土节点的非线性分析提供弹塑性模型。

关键词：型钢超高强混凝土；轴压比；体积配箍率；恢复力模型

在前人研究[1-11]的基础上，通过分析型钢超高强混凝土边节点的受力特点及传力机理，并对试验数据进行多项式拟合，建立型钢超高强混凝土边节点的恢复力模型，建议的三折线模型考虑了轴压比、配箍率对节点组合体抗震性能的影响，与试验结果吻合较好，可用于型钢超高强混凝土节点的弹塑性分析。

1试验概况

1.1试件设计

本次试验选取常规框架结构中相邻梁柱反弯点之间的典型单元作为研究对象。当多层框架层高相同时，在水平地震作用下，梁柱反弯点分别处于1/2梁跨和1/2柱高处。轴压比选择0.25、0.38、0.45三个等级。本次试验共设计6个试件，试件的截面尺寸完全相同，试件尺寸及配筋情况如图1所示。所有框架柱的混凝土强度等级均为C100，框架梁的混凝土强度等级为C40。各试件试验参数见表1，钢材的力学性能参数如表2、表3所示。

图1　试件尺寸及配筋

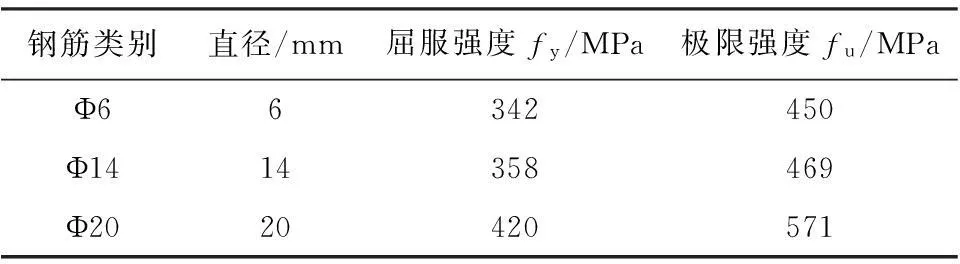
表2　钢筋力学性能

表3　型钢力学性能

1.2加载装置

试验采用拟静力加载，柱顶采用液压千斤顶施加轴向荷载，梁端为自由端,施加等量反对称低周往复荷载[12]，试验加载装置示意图如图2所示。

图2加载装置

加载制度采用力-位移混合控制，具体加载制度参照文献[12]。

1.3试验结果

所有试件在试验结束时均发生梁端塑性铰破坏，试件骨架曲线特征点的试验结果见表4。从表4中可以看出，随着轴压比的增大，试件的延性呈减小趋势，随着体积配箍率的增大,试件的延性呈增大趋势。在体积配箍率相同的情况下，当试验轴压比从0.25增大至0.45时，位移延性系数从5.70(SRUHSC-2)减小至3.28(SRUHSC-4)。

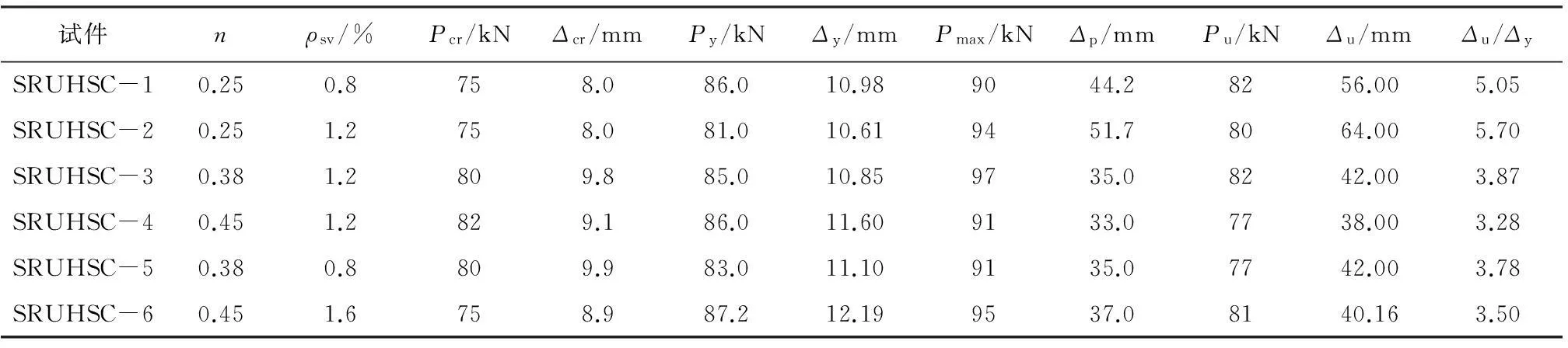
表4　骨架曲线主要特征点试验结果

为了直观对比不同轴压比和配箍率下的骨架曲线，本文对骨架曲线相对于屈服特征点进行无量纲化处理，处理后的曲线如图3所示。由图3可知，轴压比与配箍率对骨架曲线的弹性阶段影响不大，而对试件屈服后强化阶段的长度影响显著，轴压比较小的试件，强化段较长，且承载力提高显著，而轴压比较大的试件则强化段较短，屈服后很快进入强度退化阶段，骨架曲线下降段较轴压比小的试件更为陡峭。

图3经无量纲化的骨架曲线

2建议的恢复力模型

2.1骨架曲线的确定

由图3可知，在P-Δ骨架曲线中开裂点无明显的拐点，说明开裂对节点组合体试件的刚度影响不明显。这主要是由于轴力的存在，节点核心区裂缝发生延迟并得到限制，因此，为简化，不考虑开裂点的影响，建议的型钢超高强混凝土边节点恢复力模型采用三折线模型[12-14]，分为弹性段、强化段和强度退化段三个阶段。这三个阶段中包括4个起始特征点：坐标零点、屈服点、荷载峰值点和极限荷载点。

2.1.1弹性刚度

从图3中可以看出，轴压比和配箍率对试件弹性刚度的影响不显著，因此，本文只考虑了混凝土强度、钢材强度、截面尺寸对弹性刚度的影响。参照结构力学中，悬臂梁的抗侧移刚度表达式，节点组合体的弹性刚度可表示为：

(1)

其中：L为梁计算长度；I为截面惯性矩；E为弹性模量。

而当节点组合体屈服时，梁端已开裂，开裂截面的形心轴及截面惯性矩随之改变，因此在计算节点组合体的弹性刚度时，截面的惯性矩应为开裂截面惯性矩,即：

(2)

其中截面的中和轴高度可通过截面面积矩平衡关系计算,即：

(3)

开裂截面惯性矩可根据弹性理论公式计算,即：

(4)

2.1.2屈服荷载

在荷载达到屈服值之前，节点组合体试件基本处于弹性阶段，屈服荷载计算公式可表示为：

(5)

My为截面的屈服弯矩，l为梁的计算长度。根据《型钢混凝土组合结构技术规程》[15](JGJ-138-2001)，可按下式计算：

(6)

(7)

2.1.3屈服位移

根据三折线模型，将框架节点屈服前的骨架曲线简化为连接原点和屈服点的直线，因此，弹性刚度为屈服荷载与屈服位移的比值，即

(8)

由此可求屈服位移为：

(9)

其中：Δy为屈服位移；Py为屈服荷载；ke为弹性刚度。

2.1.4峰值荷载

根据公式(6)、式(7)计算，钢筋与型钢的抗拉强度取曲线峰值时对应的实测极限强度。

2.1.5峰值位移

对于轴压比较小的试件，骨架曲线强化段较长，根据三折线模型，强化段可简化为屈服点与峰值荷载点的直线段。从图3中可以看出，轴压比对强化段的影响显著。本文通过对试验结果进行多元线性回归，可得：

(10)

其中：Δp为峰值位移；Δy为屈服位移；n为轴压比

2.1.6极限荷载

极限荷载取荷载下降至峰值荷载的85%时对应的值，即：

Pu=0.85Pmax

(11)

2.1.7极限位移

根据位移延性系数的定义，可知：

Δu=μΔy

(12)

式中：Δu为极限位移；Δy为屈服位移；μ为位移延性系数。

从图4可知，轴压比、配箍率对位移延性系数影响显著[16]，利用多元线性回归得出位移延性系数与轴压比、配箍率的关系式为：

μ=7.6-14.9n+1.22ρv+1.1nρv

(13)

图4不同参数下的位移延性系数

2.2建立恢复力模型

2.2.1卸载刚度的确定

卸载刚度与轴压比的关系如图5所示，从图5可以看出：轴压比对卸载刚度的影响并不明显，因此，本文不考虑轴压比对卸载刚度的影响，根据试验数据可得出，卸载刚度与位移幅值的关系为：

(14)

其中：ku为卸载刚度；Δ为实际位移；Δy为屈服位移。

图5不同轴压比下的卸载刚度

2.2.2再加载刚度的确定

从试验记录的滞回曲线可知，随着位移幅值的增大，节点组合体均出现强度退化的现象，而由图6可知，构件的强度退化不仅与位移幅值有关，还受轴压比的影响，当轴压比增大时，强度退化现象越明显；当配箍率增大时，强度退化曲线趋于平缓[13-16]。因此，试件的再加载刚度不仅与材料的力学性质及位移幅值有关，还受轴压比与体积配箍率的显著影响。本文利用试验数据，回归得到再加载刚度与位移幅值、轴压比及体积配箍率的关系表达式为：

kr=ke(0.994-0.3i+0.0197i2+1.02n-

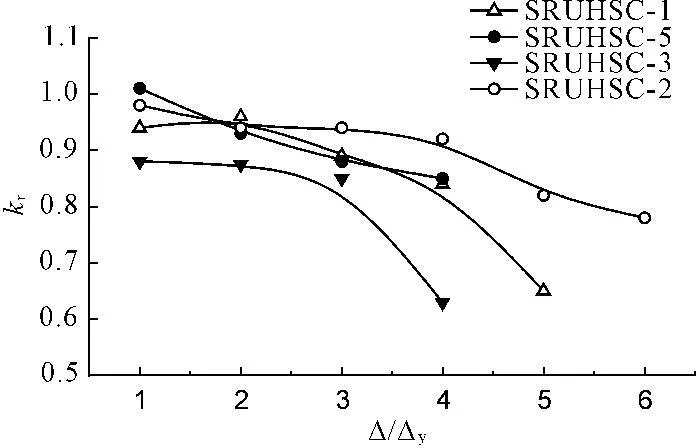
(15)

图6不同参数下kr-Δ/Δy曲线

2.2.3滞回规则

通过对型钢超高强混凝土节点滞回特性的分析，可归纳出型钢超高强混凝土节点恢复力模型(见图7)的滞回规则：

(1) 在构件尚未屈服时，加载路径与卸载路径均沿着骨架曲线的弹性段GA段；

(2) 构件屈服后，加载路径沿着骨架曲线进行(如图AB段)，卸载刚度根据不同位移幅值按公式(14)确定完整的路径如图7所示。

(3) 反向加载和再加载路径：当构件受力尚未超过屈服强度时，反向加载路径由卸载后Δ轴上相应点指向该方向骨架曲线上的屈服点；当构件受力超过骨架曲线的屈服点后，强度开始退化，滞回路径沿DEFJD进行。再加载刚度由公式(15)确定。

3模型验证

由以上建议的恢复力模型计算得到各节点组合体试件的滞回曲线如图8所示。从图中可知，计算所得的滞回曲线与试验结果较为吻合。本文建议的恢复力模型可以为边节点抗震性能和动力反应计算提供参考。

4结论

(1) 轴压比影响型钢超高强混凝土框架边节点滞回特性主要体现在影响试件骨架曲线的强化段长度，从而影响试件的延性。轴压比越小，骨架曲线强化段越长，试件的延性越好，轴压比越大，骨架曲线强化段越短，试件的延性越差，出现滞回环不稳定现象，突然丧失对轴向荷载的承受力。

(2) 轴压比与配箍率均是影响型钢超高强混凝土边节点试件强度退化的重要因素，从而影响曲线的反向加载与再加载刚度。当轴压比增大时，强度退化现象越明显；当配箍率增大时，强度退化曲线趋于平缓。

图7建议的恢复力模型

(3) 结合骨架曲线的特征点及滞回规则，通过理论计算及试验数据回归分析提出了综合考虑轴压比与配箍率对边节点滞回特性影响的型钢超高强混凝土边节点恢复力模型，并与试验曲线吻合较好。

参考文献：

[1]张品乐.短肢剪力墙抗震性能试验研究及损伤分析[D].西安：西安建筑科技大学，2011.

[2]郭子雄，吕西林.高轴压比框架柱恢复力模型试验研究[J].土木工程学报，2004, 37(5):32-38.

[3]李晓蕾，李青宁.钢筋混凝土短肢剪力墙恢复力模型研究[J].地震工程与工程震动，2014,34(5):100-107.

[4]杨春,李光星,吴轶,等.超限型钢混凝土框支剪力墙结构抗震性能评估[J].华南理工大学学报,2013,41(3):35-42.

[5]蒲心诚，王志军，王冲，等．超高强高性能混凝土的力学性能研究[J]．建筑结构学报,2002,23(6):49-55.

[6]徐亚丰，汤泓，陈兆才，等.钢骨高强混凝土框架节点恢复力模型的研究[J].兰州理工大学学报，2004,30(5):116-118.

[7]杨勇，闫长旺，贾金青，等.钢骨超高强混凝土柱-混凝土梁节点恢复力模型[J]. 土木工程学报，2014,47(S2):193-197.

[9]Zhao Jun, Dun Huahua. A restoring force model for steel fiber reinforced concrete shear walls[J]. Engineering Structures, 2014,75:469-476.

图8计算滞回曲线与试验结果比较

[10]Dan D, Fabian A, Stoian V. Theoretical and experimental study on composite steel-concrete shear walls with vertical steel encased profiles[J]. Journal of Constructional Steel Research,2011,67(5):800-813.

[11]Quiroz L G, Maruyama Y, Zavala C. Cyclic behavior of thin RC Peruvian shear walls: full-scale experimental investigation and numerical simulation[J]. Engineering Structures， 2013，52(9):153-67.

[12]中国建筑科学研究院.建筑抗震试验方法规程:JGJ101-96[S].北京：中国建筑工业出版社，1996:9-13.

[13]曾磊，许成祥，郑山锁，等.型钢高强高性能混凝土框架节点P-Δ恢复力模型[J].武汉理工大学学报，2012,34(9):104-108.

[14]李俊华，李玉顺，王建民，等.型钢混凝土柱粘结滑移本构关系与粘结滑移恢复力模型[J].土木工程学报，2010,43(3):46-52.

[15]中国建筑科学研究院.型钢混凝土组合结构技术规程:JGJ-138-2001[S].北京：中国建筑工业出版社，2001:10-16.

[16]阎奇武，唐莹莹，陈康华.组合连梁与墙肢节点恢复力模型试验研究[J].中南大学学报，2009,40(2):504-511.

[17]刘伟，贾金青，李勇，等.型钢超高强混凝土边节点抗震性能研究[J]．武汉理工大学学报:交通科学与工程版，2014，38(6):1333-1337.

Restoring Force Model for SRUHSC Exterior Joints

LIU Wei1, JIA Jinqing1, TU Bingxiong2

(1.DalianUniversityofTechnology,StateKeyLaboratoryofCoastalandoffshoreEngineering,Dalian,Liaoning116024,China;2.CollegeofCivilEngineering,HuaqiaoUniversity,Xiamen,Fujian361021,China)

Abstract：Six steel reinforced ultra high strength concrete (SRUHSC) frame exterior joints were tested under cyclic loading. Based on the test results, the effects of the axial compression ratio and the ratio of stirrup on the seismic behavior were investigated. Based on the experimental observation, a restoring force model for SRUHSC exterior joints was proposed, which is capable of considering the effect of the axial compression ratio and the ratio of stirrup on the hysteretic characteristics of the joints. It is showed that axial compression ratio and the ratio of stirrup have different level of influence to the feature points of skeleton curve. The proposed restoring force model is in good agreement with the test results and can be applied to nonlinear analysis of SRUHSC joints.

Keywords:steel reinforced high strength concrete; axial pressure coefficient; ratio of stirrup; restoring force model

文章编号：1672—1144(2016)01—0112—06

中图分类号：TU378.2

文献标识码：A

作者简介：刘伟(1984—)，女，山东济宁人，博士研究生，研究方向为型钢超高强混凝土组合结构抗震性能。 E-mail: qiuniao1984@163.com通讯作者：贾金青(1963—)，男，河北沧州人，博士，教授，主要从事型钢超高强混凝土组合结构方面的研究。 E-mail: keyknown@163.net

基金项目：国家自然科学基金项目“基于延性的型钢超高强混凝土框架结构体系抗震性能与抗震设计关键技术研究”(51178078)

收稿日期：2015-09-11修稿日期：2015-10-09

DOI:10.3969/j.issn.1672-1144.2016.01.021