多弯段溢洪道加设导流墩糙条后水流三维数值模拟

李锦艳，牧振伟，李　新

(1.新疆农业大学 水利与土木工程学院， 新疆 乌鲁木齐 830052；

2.新疆额尔齐斯河流域开发工程建设管理局， 新疆 乌鲁木齐 830000)



多弯段溢洪道加设导流墩糙条后水流三维数值模拟

李锦艳1，牧振伟1，李新2

(1.新疆农业大学 水利与土木工程学院， 新疆 乌鲁木齐 830052；

2.新疆额尔齐斯河流域开发工程建设管理局， 新疆 乌鲁木齐 830000)

摘要：“635”水库为多弯段溢洪道，为了充分体现加设导流墩糙条等辅助消能导流措施对多弯段溢洪道水流的影响，通过标准k—ε模型和VOF多相流方法并建立三维数学模型，得到了溢洪道各典型断面流速大小以及水深的分布规律。数值模拟结果与模型试验结果对比表明，使用的数值模型能较精确地模拟加设辅助措施后溢洪道的水流流态。结果表明溢洪道水流由于受导流墩糙条等辅助消能导流措施的影响，能有效控制弯道环流的发生以及缩短纵向流速分布调整的距离。从而为多弯段溢洪道的水力设计提供可靠的理论依据。

关键词：溢洪道；导流墩；糙条；VOF方法；三维数学模型

溢洪道是主要的泄水建筑物之一，溢洪道可分为直线型和曲线形。而溢洪道平面布置常常受到地形、枢纽整体布置等因素约束，所以在平面上布置成圆弧形的弯道形式[1]。当水流流经弯道时，由于惯性离心力和坡降共同作用，以致于溢洪道的弯道水流水力特性变得极为复杂。而“635”水库溢洪道有5个弯道，且两个消力池都布置在弯道上，是一种不多见的溢洪道布置型式。

针对弯道的研究主要集中在天然河道。1876年，Thomson J.首次通过试验研究弯道环流以来，弯道的研究一直受到关注。Kikkawa等[2]提出的弯道二维水流模型，模型采用了标准矩形断面的单弯道,结果吻合较好；夏云峰[3]在平面上采用了非正交曲线，垂向采用了坐标变换模式，建立了非交错网格，且模拟了南京河段天然的“S”型弯道水流流动；而Reinauer R等[4]应用特征线的理论求解了浅水方程，并且应用于弯道急流，从而得到了较好的结果。而弯道的存在，会导致弯道产生环流、横向水面超高、横向水流流速分布不均等问题。

多弯段溢洪道相对天然河道而言,坡比降很大,以致于存在的问题更为突出。“635”多弯段溢洪道在60 m长度的坡降达到15 m,而且前两个弯道十分接近,很有可能产生波的叠加,从而造成水面起伏较大。假如处理不当,将会对溢洪道辅助消能措施产生很大的影响。

1工程概况

“635”水利枢纽大坝为黏性土心墙砂砾石坝，坝高为71.5 m，坝长约320 m，坝顶高程是650 m。“635”溢洪道工程由引渠段、控制段、人工泄槽及天然泄槽段四部分组成。溢洪道横断面为矩形断面,底宽54 m,中心线纵坡分别为：1∶20、1∶10、1∶60、1∶50、1∶19、0。整个溢洪道共有5个弯道,天然泄槽段、1∶4陡坡以及上、下两个消力池都在弯道上。第一弯道半径很小为57 m，转角α=28.59°，底坡陡(i=1/20)；第二弯道半径较大，转角α=40°,底坡缓(i=1/60)；第三弯道半径较大,转角较小α=20°，底坡陡(i=1/19)；第四弯道半径较大，转角较小α=22.5°且为平坡；第五弯道半径较小,转角α=30°,但坡很陡(i=1/4)。根据已建工程实际经验得出弯道半径一般应大于6倍～10倍流道底宽。而“635”溢洪道为了利用天然泄槽,最大转弯半径仅是溢洪道底宽的3倍,最小转弯半径只有1.05倍流道宽。

当溢洪道通过800 m3/s的流量时，凹凸岸水深及流速相差较大，两弯道之间的顺直段无法满足水流流出弯道后纵向流速分布至正常所需要的调整段的长度。弯道半径小、坡度陡、流速大、环流强度大、流态复杂及凹凸岸水深相差较大等特点，仅取溢洪道的前两个典型弯道段模拟研究，原方案平面布置图见图1。为了满足溢洪道水流泄流能力以及控制弯道环流的发生和发展，以及缩短纵向流速分布调整所需要的距离，使得弯道段的水流较快地在横断面上重新均匀分布。孙娟等[5]对“635”溢洪道原方案进行修改，应用导流墩糙条等辅助消能导流措施联合形式来削弱水流紊流强度，从而控制弯道折冲波的发生。修改方案平面布置图见图2。

图1　原方案平面布置图(单位：m)

图2修改方案平面布置图(单位：m)

2数学模型

2.1控制方程

考虑是不可压缩水流流动问题，采用k—ε紊流模型，方程如下：

连续方程：

(1)

动量方程：

(2)

k方程：

Gk-ρε-YM

(3)

ε方程：

(4)

其中：

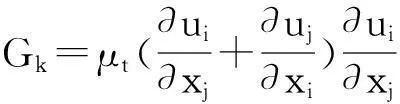
式中：Gk是由于平均速度梯度引起的湍动能；YM是可压缩湍流脉动膨胀对总耗散率的影响；C1ε、C2ε是经验常数，默认C1ε=1.44、C2ε=1.92；σk和σε分别为湍动能及湍动耗散率所对应的湍流普朗特数。默认σk=1.0、σε=1.3；β是热膨胀系数；Mt是湍动马赫数；ɑ为声速。方程各项参数见文献[6]。

2.2求解方法及边界条件处理

数值计算采用了基于同位网格SIMPLE(Simi-Implicit Method for Pressure-Linked Equations, SIMPLE)法，采用了有限体积法对控制方程组进行了离散[7-13]。而进口断面设置为速度进口边界条件，断面的流速呈矩形分布。出口断面水流充分发展，假设出口断面所有变量法向梯度为零。压力值设置为大气压。固壁上采用无滑移的边界条件。采用壁面函数法来计算近壁区的紊流。

2.3计算区域及网格剖分

为了充分体现导流墩、糙条对溢洪道水流影响，模拟计算区域包括溢洪道前两个弯道、8条导流墩、4条导墙及7条糙条。由于所模拟的计算区域较大，采用结构化和非结构化网格相结合的方法[14]，网格单元数为68 973个。划分网格时，针对重点部位如弯道进行适当的加密，一般的部位适当放宽的原则进行。整个计算区域网格划分为图3所示。

图3溢洪道数值计算网格划分

2.4计算结果与分析

原方案中未加设任何消能导流措施，孙娟等[5]经过物理模型试验得出，水流在弯道中运动时受惯性力影响产生横向比降与弯道环流，环流强度大，流态紊乱。修改方案中在弯道Ⅰ段加设导流墩糙条等消能导流措施，有效控制了弯道的发生和发展，缩短了纵向流速分布调整的距离，使水流能较快地在横断面上重新分布。

在研究溢洪道水流流态时，原方案与修改方案数值模拟研究对比分析各典型断面的水-气两相各自所占的比例，得到溢洪道弯道加设导流墩糙条等消能导流辅助措施前后各断面水流流态[15]，如图4所示。

由图4弯道断面水-气两相图可以看出，在弯道处加设导流墩糙条等辅助消能导流措施前后，图4(a)与图4(b)及图4(c)与图4(d)进行对比分析，加设辅助消能导流措施后，弯道处均有效降低了水流的水面凹深度与长度；半径小的弯道加设导流墩和导墙有助于调整控制弯道内水流流态及流速的控制。并有效控制了弯道漩涡的产生，并削弱了水流冲击力。

为了进一步确认数值计算的准确性，数值模拟计算结果与物理模型试验进行对比，得出各典型断面的水深及流速水力要素见表1、表2。

表1　各典型断面水深水力要素

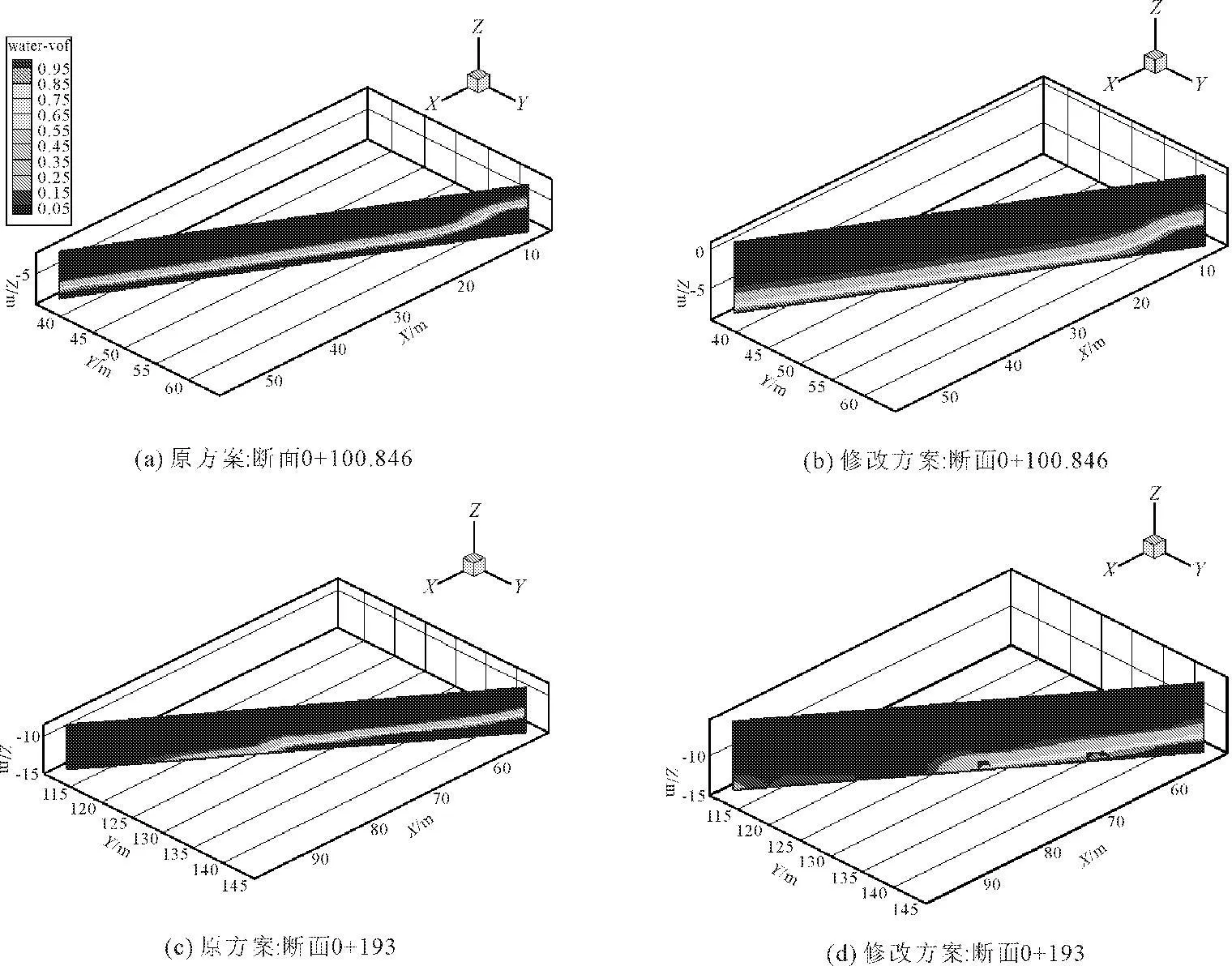
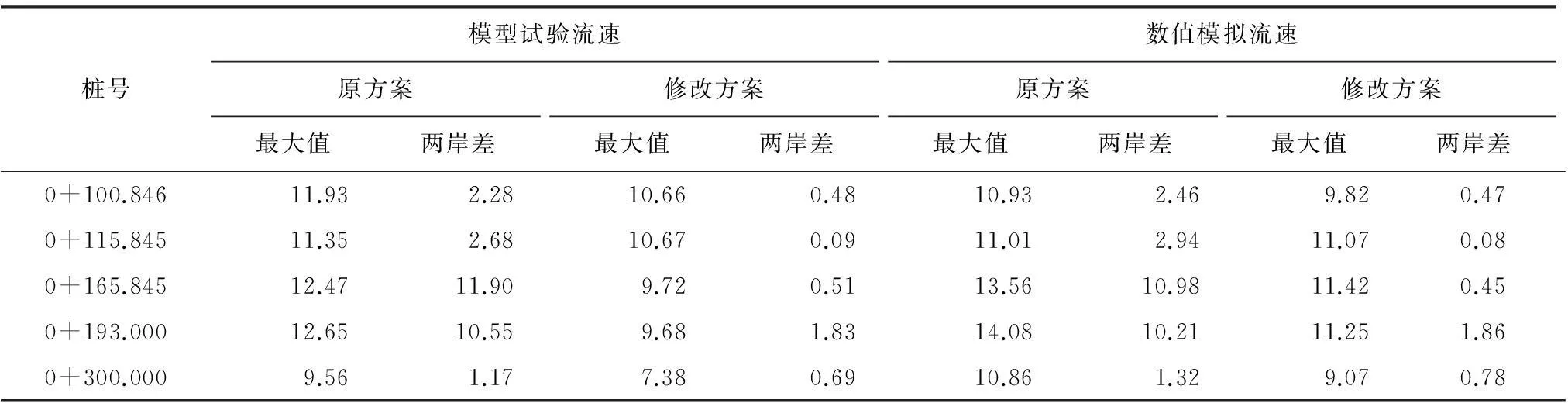
图4　弯道断面水-气两相图

表1、表2为多弯段溢洪道数值模拟与物理模型典型断面的水深和流速计算值与实测值对比。从表中可以看出计算值与实测值相差不大。具体分析数值模拟与物理模型水深与流速的相对误差见图5。

从图5中可以看出，数值模拟计算值与物理试验值基本吻合。说明数学模型可以较好地对溢洪道水流流态进行模拟。计算结果表明，设置导流墩糙条等辅助措施有效地改善了弯道流态，减小了横向超高，有效调整了横向流速分布。

3结论

(1) 弯道环流及折冲波的形成是由于弯道半径及角度小，无法满足水流恢复到正常所需的调整距离。加设辅助消能导流措施后，有效地降低了弯道凹岸水面高度或水深，减少了凹岸壅水范围,减少水流折冲波，有助于控制弯道环流的发生和发展。

(2) 数值模型能够准确模拟多弯段溢洪道三维水流动力特性，得到了溢洪道典型断面的水深流速等重要水力参数。数值模拟方法有利于进行多方案的比较，布置适当尺寸的导流墩糙条等辅助消能导流措施可以节约大量工程费用，较快地优化设计方案。

(3) 数值模拟结果与试验结果吻合较好，采用VOF方法可以准确追踪多弯段溢洪道自由水面，且水面平滑，与此同时证明了所采用计算机模型及计算机程序是可行的，数值模拟方法适用于溢洪道等大型水工建筑物内的水流流态。

图5各典型断面水力要素对比

参考文献：

[1]周勤,伍超,赵元弘，等.“S”型溢洪道水流特性试验与数值模拟研究[J].水力发电学报,2005,24(3):78-82.

[2]Kikkawa H. Flow and bed toppgraphy in curved open channels[J]. Journal of Hydraulic Division，1976,102(9):1327-1342.

[3]夏云峰.一种简便的非交错曲线网格三维水流数值模型[J].水动力学研究与进展,2002,17(5):638-646.

[4]Reinauer R, Hager W H. Supercritical bend flow[J]. Journal of Hydraulic Engineering, 1997,123(3):208-218.

[5]孙娟,陈晓梅.导流墩和糙条对溢洪道弯道水流的调整作用[J].新疆水利,2001(6)：6-9.

[6]朱红钧,林元华,谢龙汉.FLUENT流体分析及仿真使用教程[M].北京.人民邮电出版社,2010:107-108.

[7]李斌华,肖艳,刁明军.数值模拟在溢洪道体形优化中的应用[J].水力发电,2010,36(3):36-38.

[8]刘士和,段红东.挑流水舌运动数值模拟[J].武汉大学学报:工学版,2004,37(6):1-4.

[9]杨利.溢洪道挑流消能段水气两相流数值模拟研究[D].济南:山东大学,2011.

[10]戴会超,槐文信,吴玉林，等.水利水电工程水流精细模拟理论与应用[M].北京:科学出版社,2008.

[11]董延超,郭维东,魏长勇，等.陡槽式溢洪道三维流场数值计算分析[J].人民长江,2006,37(4):69-71.

[12]Singhal A K, Athavale M, Li H Y, et al. Mathematical basis and validation of the full caviation model[J]. Journal of Fluids Engineering, 2002，124(3):617-624.

[13]张志雁,牧振伟,万连宾.克孜加尔溢洪道控制段体形优化的数值模拟[J].水利与建筑工程学报,2010,8(6):69-72．

[14]沙海飞,周辉,吴时强，等.多孔溢洪道泄流三维数值模拟[J].水利水电技术,2005,36(10)：42-46.

[15]郭瑾瑜,王均星.溢洪道中墩水翅的数值模拟[J].武汉大学学报:工学版,2013,46(5)：572-576.

3D Numerical Modeling of Water Flow of Carved Spillway after Installing Diversion Pier and Roughness Section

LI Jinyan1, MU Zhenwei1， LI Xin2

(1.CollegeofWaterConservancyandCivilEngineering,XinjiangAgriculturalUniversity,Urumqi,Xinjiang830052,China;2.XinjiangIrtyshRiverBasinDevelopmentProjectConstructionandManagementBureau,Urumqi,Xinjiang830000,China)

Abstract：“635” reservoir is a spillway of many curved segments. In order to fully reveal the influence of installing diversion pier and roughness section and other auxiliary energy dissipation and water flow piloting measures on the water flow of curved spillway, through standard k—ε model and VOF multiphase flow method a three-dimensional mathematical model was developed and the distribution law of the depth of water and the flow speed of each typical cross section of spillway were derived. The comparison between the numerical modeling and the model tests showed that the numerical model can accurately simulate the water flow pattern of the spillway after installing auxiliary measures. The results suggested that under the influence of diversion pier and roughness section and other auxiliary energy dissipation and water flow piloting measures, the water flow of spillway can effectively control the occurrence of water circulation of carved section and shorten the adjustment distance of longitudinal flow velocity distribution. This research could provide reliable theoretical basis for the hydraulic design of multi-curved spillway.

Keywords:spillway; diversion pier; roughness section; VOF method; three-dimension mathematical model

文章编号：1672—1144(2016)01—0091—05

中图分类号：TV651.1

文献标识码：A

作者简介：李锦艳(1993—)，女，新疆乌鲁木齐人，硕士研究生，研究方向为水力学及河流动力学。E-mail：649188672@qq.com通讯作者：牧振伟(1973—)，男(回族)，新疆乌鲁木齐人，教授，主要从事水力学及河流动力学方面的工作。E-mail：xjmzw@163.com

基金项目：新疆维吾尔自治区重点学科建设项目资助

收稿日期：2015-09-15修稿日期：2015-10-19

DOI:10.3969/j.issn.1672-1144.2016.01.017