利用收费站称重系统数据的高速公路桥梁车辆荷载效应研究

许永吉，夏樟华，宗周红

(1.福州大学 土木工程学院， 福建 福州 350108; 2.福建高速技术咨询有限公司， 福建 福州 350108；

3.东南大学 土木工程学院， 江苏 南京 210096)



利用收费站称重系统数据的高速公路桥梁车辆荷载效应研究

许永吉1,2，夏樟华1，宗周红3

(1.福州大学 土木工程学院， 福建 福州 350108; 2.福建高速技术咨询有限公司， 福建 福州 350108；

3.东南大学 土木工程学院， 江苏 南京 210096)

摘要：以一座连续刚构桥为工程背景，利用收费站称重系统数据，探索能反映实际运营状况的高速公路桥梁车辆荷载效应分析方法。利用福建省全省收费站称重系统的车辆荷载数据提取通过桥梁的车辆荷载。基于平衡更新随机过程，建立了高速公路桥梁的车辆荷载效应理论分析方法。利用连续刚构桥健康监测系统实测的车辆荷载效应，对基于收费站称重系统得到的车辆荷载效应分析结果进行验证。结果表明，基于收费站称重系统数据的桥梁车辆荷载效应计算结果与实测结果吻合较好，所建立的方法可以得到不同荷载重现期内的荷载效应最大值分布，并用于桥梁安全性能评估和预测。

关键词：桥梁工程；连续刚构桥；平衡更新过程；收费站车辆荷载；车辆荷载效应；健康监测

车辆荷载是对桥梁进行承载能力、可靠性分析及剩余寿命预测的依据。目前，在车辆荷载效应的研究过程中，采用随机过程描述车辆荷载，得到车辆荷载效应的概率分布模型和车辆荷载在评估期内的最大值概率分布是一种常用方法。国外较早开展车辆荷载方面的研究，包括滤过泊松随机过程[1]、白噪声随机场[2]、车辆连续到达的平衡更新过程[3]。我国学者在实际交通荷载调查的基础上，也进行了车辆荷载模型方面的研究，主要通过实际统计的车辆荷载信息，对各种随机过程进行验证和发展，得到适合我国的车辆荷载模型[4-8]。在桥梁车辆荷载效应的分析过程中，如何定量描述评估周期内某座桥梁的车辆车载效应的大小，需要知道评估桥梁路段的交通荷载状况及车辆荷载效应极值。当前推导车辆荷载极值的主要方法可分为Nowak方法和Rice公式方法两种[9-12]。在此基础上，部分学者发展了一些新的方法。阮欣等[13]提出了采用合成车流方法模拟交通流并实现荷载效应预测，同时检验了Rice公式对合成交通车流的车辆荷载效应的模拟及其极值预测过程。Caprani C C等[14]应用预测可能性的方法来评估荷载效应极值分布。李植淮等[15]提出了基于GPD(Generalized Pareto Distribution)模型的车辆荷载效应极值估计方法，该方法放弃了车流量稳定的假定，更合理地预测未来车辆荷载效应的极值。

目前车辆荷载信息的调查主要采用动态称重系统(WIM系统)，但是安装WIM系统价格比较昂贵，而且我国地域辽阔，通过WIM系统进行全面调查比较困难。由于我国的高速公路都采用了计重收费的管理办法，如果有效地利用高速收费站称重系统的数据进行车辆荷载的采集和分析，可以极大地节省费用，并对不同区域的桥梁车辆荷载效应进行有效评估。从这个角度出发，在已有研究的基础上，提出了一种利用高速公路收费站称重系统数据进行大跨度连续刚构桥车辆荷载效应评估的方法，并利用健康监测系统的实测荷载效应进行验证，推动了高速公路桥梁车辆荷载模型研究的发展。

1背景工程简介

该桥梁(见图1)是沈阳至海口国高主干线福鼎至宁德高速公路的特大桥。主桥为145 m+2×260 m+145 m四跨预应力混凝土连续刚构桥，单幅桥面宽为12 m，设计荷载为汽超-20、挂-120，无人群荷载。桥梁2003年7月建成通车。桥梁上部结构按全预应力混凝土设计，主墩均采用双柱薄壁墩。

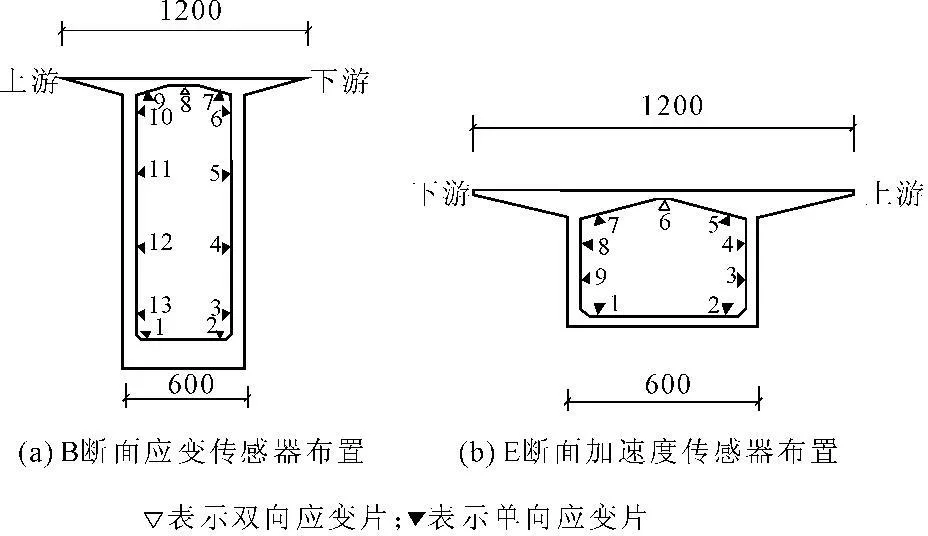
为了对桥梁的综合工作性能进行监测和评估，安装了桥梁健康监测系统，由传感系统、数据采集和预处理系统、远程传输系统、电源管理系统和评估系统等组成。该系统包括应变计、加速度传感器、拉线位移传感器、动位移传感器、温度传感器等各类传感器共131个，见图2。其中，62个应变测点分别布置在跨中、1/4跨及墩顶共7个截面，典型截面布置见图3。

图1　桥梁图片

注：方框内：A加速度传感器；D动位移传感器；S应变传感器；LD拉线位移传感器；T温度传感器。字母后数字表示传感器数量。

图3应变测点布置(单位:cm)

2收费站称重系统数据的筛选

以所研究的连续刚构桥为例，根据其入口收费站和出口收费站记录，利用全省的收费站和桥梁桩位资料，通过Excel VBA编制程序筛选得到经过B道的车辆在收费站的交通监测数据，流程见图4。经过对收费站交通调查数据的筛选处理，共得到两个月总数为542 985条车辆称重数据，其中客车记录342 347条，货车记录200 638条。记录中包括了出入口收费站名，进出高速公路的时间，车辆的轴型、车辆的各轴轴重、车辆的总重等信息。由于车辆总重在3 t以下的车辆对桥梁的损伤影响可以忽略不计[16]，以其中的228 341条车辆总重大于3 t的收费站车辆称重数据作为统计分析的样本。

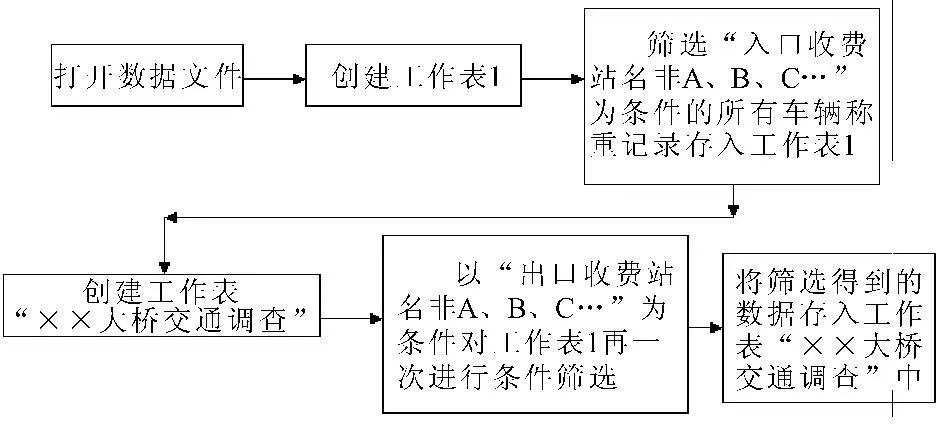
图4交通数据筛选流程图

3基于平衡更新过程的车辆荷载模型

3.1车辆车重分布

对收费站的车辆称重记录中车重信息的分析可得到通过下白石大桥车辆的车重分布。首先得到车重和出现频率之间的关系，并进行参数拟合。经参数拟合可知，车重服从多峰正态分布，曲线函数表达式如式(1)，R2=0.9962，很接近1，说明拟合函数能够很好地反映下白石大桥车辆荷载的车重统计规律。

(1)

3.2车辆荷载的统计特征和统计参数

我国“公路桥梁车辆荷载研究”课题组在20世纪90年代进行了车辆荷载调查，根据全国交通量调查长期观测资料，得到公路桥梁车辆荷载的两个分布类型，见表1[17]。其中，密集运行状态为两辆相随汽车的时间间隔在3 s以下，包括堵车状态；一般运行状态为两辆相随汽车的时间间隔在3 s及3 s以上。由于收费站称重系统的交通调查数据只能得到下白石大桥上车辆的车重分布，缺少实时称重系统所测量的车重、车长、车间距、连续到达时间间隔等车辆荷载参数。因此车辆连续到达时间间隔、连续到达车间距等的统计参数将使用表1的统计资料。

表1　车辆荷载概率分布类型和分布参数

3.3车辆通过桥梁的模拟

对车辆荷载的描述也就是对车辆通过桥梁的过程进行模拟是建立车辆荷载模型的基础。对于既有桥梁在不同的交通运行状态，车速v取不同的值，各车辆的连续到达过程为平衡更新过程[4]，即两辆车连续到达的时间间隔(第i辆车与第i+1辆车通过同一测点的时间差)为平衡更新过程。采用平衡更新过程求解不同长度和不同数量车辆通过桥梁的概率分布。

3.4车队影响线面积最大值

3.4.1连续刚构桥有限元模型

根据竣工图纸，建立大桥有限元模型，共有28 250个单元，42 975个节点。全桥采用Solid45单元模拟，用Combin14模拟主桥的边界条件。主桥箱梁采用C60混凝土，弹性模量取值为3.65×104MPa；桥墩墩身均采用C50混凝土，弹性模量取值为3.5×104MPa；桥墩承台采用C30混凝土，弹性模量取值为3.0×104MPa。混凝土的密度取为2 550 kg/m3，泊松比为0.167。用Combin14模拟主桥的边界约束，采用刚度相同的纵、横向弹簧来模拟主桥两端部的支座和伸缩缝对主桥的约束以及纵横向的摩擦效应，并采用竖向弹簧模拟支座的作用，竖弹、纵向和横向弹簧刚度取值分别为13.0×107N/m、7.5×107N/m和9.0×106N/m。实测和计算动力特性值对比见表2，竖向最大误差为5.13%,可知有限元模型能反映桥梁当前状态。

3.4.2最大影响线面积求解

车辆队列通过桥梁产生的荷载效应可以由一个特定的车队布置在相应效应动力影响线上计算得到，当荷载效应影响线的长度大于等于20 m时，车轴布置的影响可以忽略不计[4]。长度为lc的车队可等效为一个长度为lc、大小为w/lc(w为车队的总重)的均布荷载，并根据最大影响线面积A求解最大荷载效应。

表2　实测与计算的动力特性值对比

车队对应的影响线面积为A′，则A′可以根据车队长度lc，桥梁影响线长度L以及车队距离影响线端点的长度计算得到。对于连续刚构桥影响线较为复杂，无法得到解析表达式，采用数值的方法来获得A(L，lc)在任一点处的近似值。

因为，在区间[a,b]上的有界函数f(x)，其定积分可通过式(2)计算。

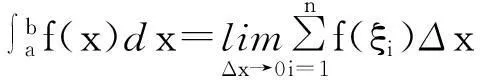
(2)

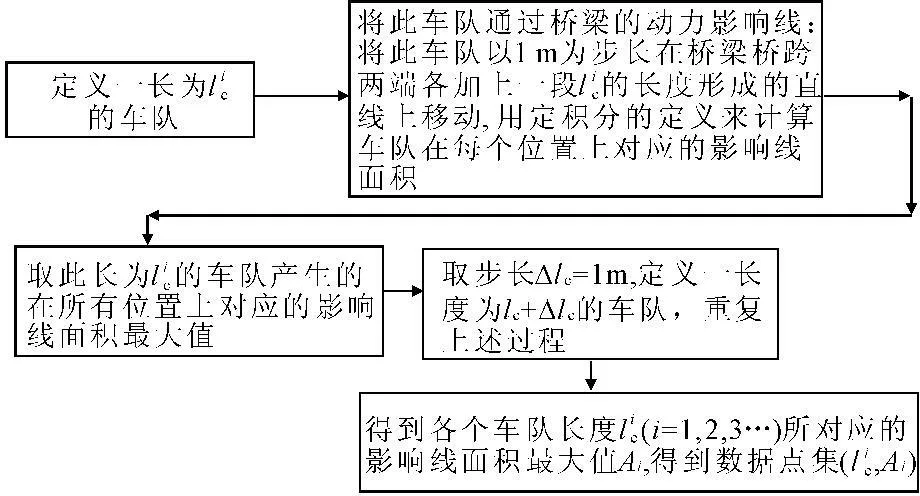
图5影响线面积最大值求解过程

3.5车队总重的概率密度函数

对于由n辆车前后跟随组成的车队，总重的概率密度函数可由车重概率密度函数卷积得到。设f(w)为车重概率密度函数，由收费站车辆称重数据可知，通过下白石大桥的车辆最小重量为wmin=7.8kN，最大车重为wmax=705.6kN，可得到车重截尾密度函数f′(w)，则两辆车的车队总重为

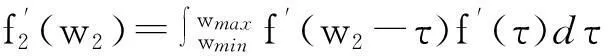
(3)

3.6车辆荷载效应最大值分布计算方法

设长度为lc和总重为wn的车队在长度为L的影响线上产生的最大荷载效应值为E，则

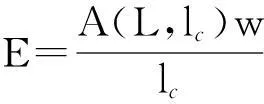
(4)

假设存在A(L，lc)的解析表达式，由随机变量函数的分布定理可知：

(5)

设fn(lc，L)为包含n辆车的特定车队通过长度为L的影响线的车队长度lc的概率密度函数，则

(6)

式中，r为长度为L的影响线上最多可布置的车辆数；lmin为车队的最小长度。

设fi(E)为第i种运行状态和影响线长度为L的情况下，荷载效应最大值的密度函数，则有

(7)

这样得到了计算车辆荷载效应最大值密度函数的理论表达式，由于该积分表达式复杂，在实际计算中可根据定积分的定义用数值方法进行计算，计算表达式如下：

(8)

4下白石大桥车辆荷载效应分析

4.1车辆荷载效应计算

由于该桥截面为箱形截面，车辆荷载的横向分布对所关注的测点处纵向应变的影响不大，且车辆单向通行，因此将其考虑为单车道桥进行计算。

由卷积公式得到连续到达的车间距见图6，对于车重分布，根据白石大桥车重分布函数，进行截尾处理和卷积后，得到车队总重概率密度函数见图7，图中的n表示车队中包含的车辆数。

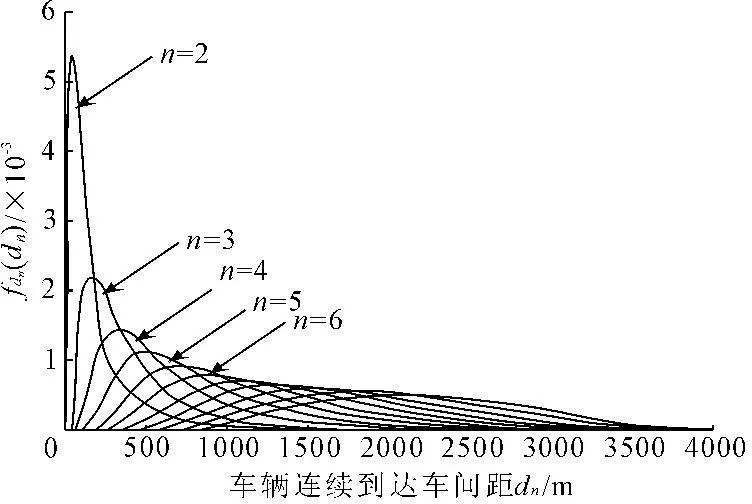
图6　一般运行状态下车辆连续到达车间距密度函数

图7车队总重密度函数

(1) 两个断面的理论计算与实测得到的两函数图形均比较接近，理论计算可较好地反映实际桥梁车辆荷载效应最大值的统计规律。

(2) E断面计算应变包含30 με～100 με的部分，这个部分对于理论计算得到的不同荷载重现期内的应变最大值分布有较大的影响。实测得到的函数图形不包括应变较大的部分，说明受到调查时间的限制，未能得到非常准确的应变最大值初始分布。由于B断面截面高度较大，且位于边跨跨中，该断面纵向应变2号测点处车辆荷载效应(应变)较小，应变分布集中在一个较小范围。

(3) 进行理论计算时所使用的“公路桥梁车辆荷载研究”课题组的交通调查结果与该桥实际的车辆荷载统计参数有差距，是导致上述两个密度函数图形有差异的最主要原因。

实测车辆荷载效应最大值初始分布与单车道的荷载效应最大值初始分布较为接近，这是由于该桥车辆单向行驶且桥上的交通流量不大(平均10 s才有一辆车进入大桥)，车辆大多相互跟随通过桥梁，极少出现两个车道上均满布车辆，车辆并列通过桥梁的情况。由于该桥截面为箱形截面，车辆荷载的横向分布对纵向应变的影响不大，故实测的车辆荷载效应最大值初始分布与理论计算的单车道荷载效应最大值初始分布相近。

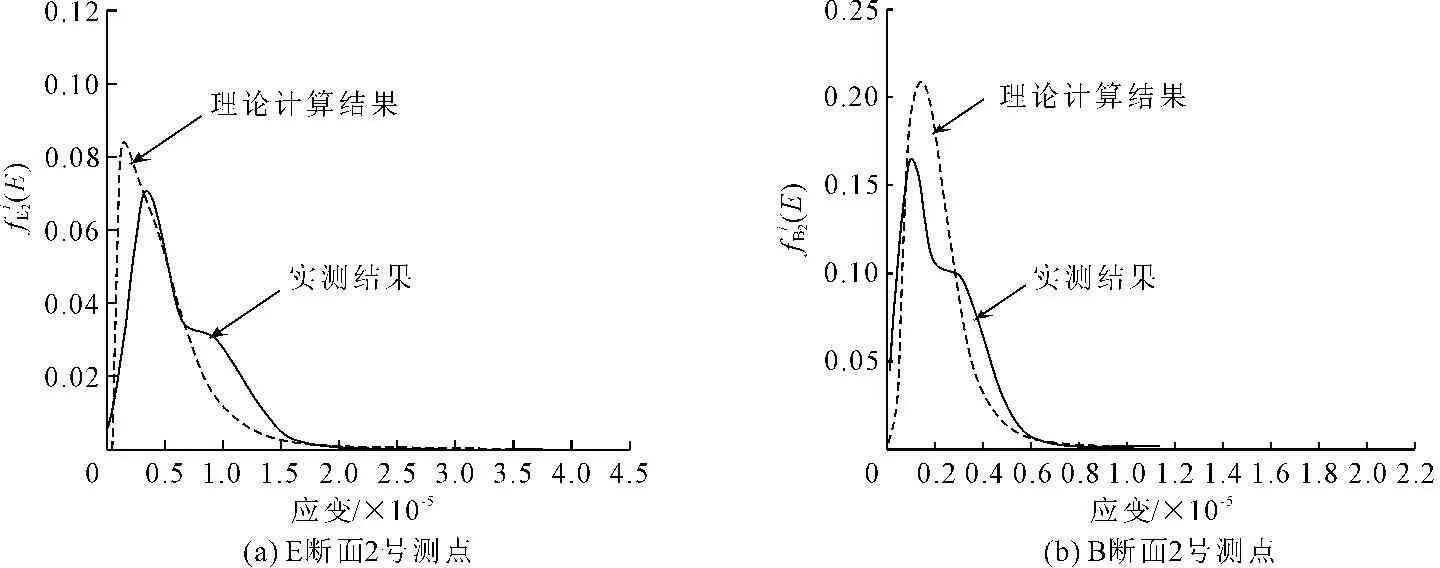
图8计算与实测得到的应变最大值密度函数比较

4.2车辆荷载效应的最大值分布

不同运行状态混合的车辆荷载效应最大值密度函数由式(9)计算得到。

(9)

其中，qk代表第i种运行状态出现的概率。

设Fm(E)为fm(E)所对应的分布函数，不同重现期内的车辆荷载最大效应分布函数FT(E)由式(10)计算得到。

FT(E)=Fm(E)N(T)

(10)

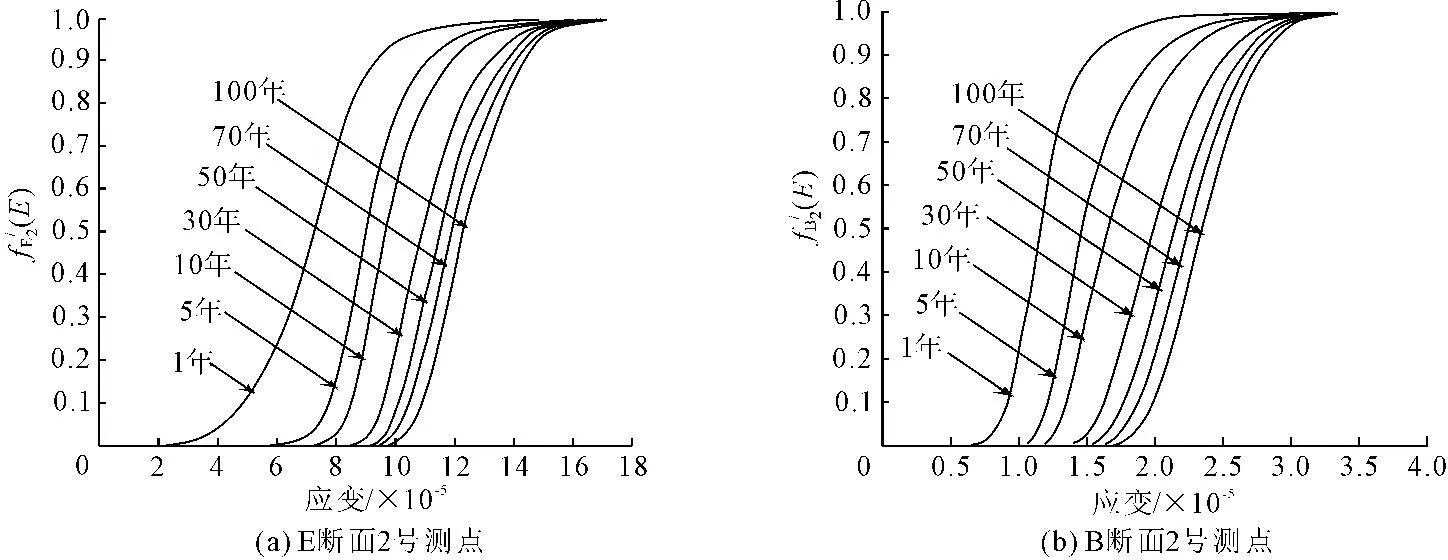
图9不同荷载重现期应变最大值分布

对不同荷载重现期应变最大值进行分布拟合可知其服从极值Ⅰ型分布：

F(x)=exp(-e-a(x-b))

(11)

式中的单位为微应变，με，E断面纵向应变2号测点不同荷载重现期内的极值Ⅰ型分布系数见表3。

表3　不同荷载重现期内的拟合系数

以理论计算得到的E断面纵向应变2号测点处应变最大值初始分布计算得到的不同荷载重现期内的应变最大值分布为基础，对大桥车辆荷载效应进行评估。得到的对比结果如表4所示，评估结果由不同荷载重现期内应变最大值分布与汽超-20三车道布置产生的荷载效应进行比较得到，还得到了不同荷载重现期内荷载效应最大值分布函数的0.95分位点超过设计荷载效应的百分比。从表中可知，大桥E断面纵向应变2号测点处车辆荷载效应(应变)最大值超过设计荷载效应的概率较大，例如荷载重现期为50年时，车辆荷载效应超过设计荷载效应的概率为0.9795。进行大桥的结构验算和荷载试验时应考虑实际的车辆荷载效应，对控制截面进行试验时应将试验荷载效应根据不同的评估基准期(荷载重现期)较汽超-20产生的荷载效应提高相应的比例，以使计算结果和试验结论符合桥梁的实际情况。

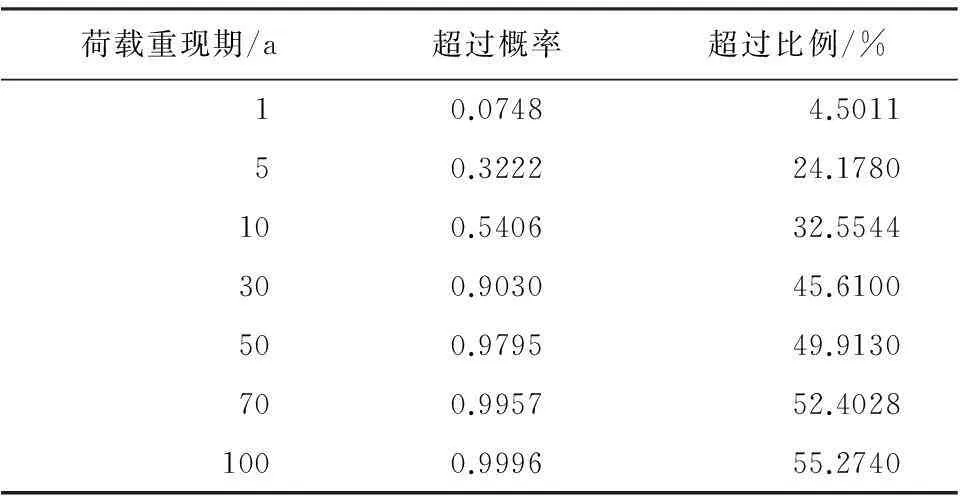
表4　不同荷载重新期内荷载效应超过

注：超过比例：(0.95分位点-设计荷载效应)/设计荷载效应

5结论

(1) 提出了利用高速公路收费站车辆称重系统进行交通调查的方法，并解决了收费站车辆称重数据记录的筛选问题，筛选得到了下白石大桥上通行车辆的称重记录。

(2) 根据收费站车辆称重系统得到的车重数据，基于平衡更新随机过程，建立了连续刚构桥的车辆荷载效应分析方法，得到了不同荷载重现期内的荷载效应最大值服从极值Ⅰ型分布。利用健康监测系统得到的实测荷载效应与计算结果较为吻合，认为所提出的方法能较好地得到实际运行车辆作用下高速公路桥梁的荷载效应。

(3) 以设计车辆荷载效应为标准对连续刚构桥的车辆荷载效应进行评估，该桥当前的车辆荷载效应最大值较设计荷载效应大4.50%。因此，进行桥梁结构验算和荷载试验时应考虑实际的车辆荷载效应，以使计算结果和试验结论符合桥梁的实际情况。

参考文献：

[1]Caprani C C, Obrien E J, McLachlan G J. Characteristic traffic load effects from a mixture of loading events on short to medium span bridges[J]. Structural Safety, 2008,30(5)：394-404.

[2]Ditlevsen O, Madsen H O. Stochastic vehicle-queue-load model for large bridges[J]. Journal of Engineering Mechanics, 1994,120(9):1829-1847.

[3]Croce P, Salvatore W. Stochastic model for multilane traffic effects on bridges[J]. Journal of Bridge Engineering, ASCE, 2001，6(2)：136-143.

[4]林升光.正常运行状态车辆荷载复合Poisson过程模型[J].福建师范大学学报:自然科学版,1995,11(2):9-14.

[5]梅刚，秦权，林道锦.公路桥梁车辆荷载的双峰分布概率模型[J].清华大学学报：自然科学版，2003，43(10):1394-1396.

[6]郭彤，李爱群，赵大亮.用于公路桥梁可靠性评估的车辆荷载多峰分布概率模型[J].东南大学学报：自然科学版，2008,38(5):763-766.

[7]王磊，张建仁.基于平衡更新过程的既有桥梁车辆荷载效应模型[J].中国公路学报，2008，21(5):50-56.

[8]宗周红，李峰峰，夏叶飞，等.基于WIM的新沂河大桥车辆荷载模型研究[J].桥梁建设，2013，43(5):29-36.

[9]周泳涛，翟辉，鲍卫刚，等.公路桥梁标准疲劳车辆荷载研究[J].公路，2009(12):21-25.

[10]Nowak A S. Live load model for highway bridges[J]. Structural Safety, 1993,13(1/2):53-66.

[11]Nowak A S, Hong Y K. Bridge live-load models[J]. Journal of Structural Engineering, 1991,117(9):2757-2767.

[12]Cremona C. Optimal extrapolation of traffic load effects[J]. Structural Safety, 2001,23(1):31-46.

[14]Caprani C C, Obrien E J. The use of predictive likelihood to estimate the distribution of extreme bridge traffic load effect[J]. Structural Safety, 2010,32(2):138-144.

[15]李植淮,李春前,孙健康,等.基于GPD模型的车辆荷载效应极值估计[J].工程力学,2012,29(S1):166-171.

[16]项海帆.高等桥梁结构理论[M].北京：人民交通出版社，2002：96-102.

[17]“公路桥梁车辆荷载研究”课题组.公路桥梁车辆荷载研究[J].公路，1997(3)：8-12.

Vehicle Load Effect of Highway Bridges Based on the Data Taken From Highway Toll Station’s Weight System

XU Yongji1,2, XIA Zhanghua1, ZONG Zhouhong3

(1.CollegeofCivilEngineering,FuzhouUniversity,Fuzhou,Fujian350108,China;2.FujianExpresswayTechnologyConsultingCo.,Ltd,Fuzhou,Fujian350108,China;3.CollegeofCivilEngineering,SoutheastUniversity,Nanjing,Jiangsu210096,China)

Abstract：In this paper, a rigid-frame bridge was selected as an example, a vehicle load effect analysis method for highway bridge using highway toll station’s weight system was analyzed. Firstly, the real vehicle load data was taken from highway toll station’s weight system, then the vehicle load effect model of highway bridges based on the theory of Equilibrium Renewal Process was established. Finally, the results were verified according to the data of the health monitoring system, and the vehicle load effect of the bridge was estimated. The results showed that the calculating results based on the highway toll station’s weight system were close to the testing ones, and the present method could be used to obtain the extreme value distribution in different load recurrence period, and apply in safety evaluation and vehicle load prediction.

Keywords:bridge engineering; continuous rigid-frame bridges; equilibrium renewal process; highway toll station’s weight system; vehicle load effect; health monitoring

文章编号：1672—1144(2016)01—0065—07

中图分类号：U441.3

文献标识码：A

作者简介：许永吉(1980—)，男，福建连城县人，博士生，研究方向为桥梁监测、评估与加固。E-mail：civil0518@163.com通讯作者：夏樟华(1980—)，男，浙江淳安县人，博士，主要从事桥梁安全性能评估和桥梁抗震研究。 E-mail：xiatian@fzu.edu.cn

基金项目：国家自然科学基金(51178101)；福建省教育厅科技项目(JA12041)；福建省重点交通科技项目

收稿日期：2015-09-11修稿日期：2015-10-14

DOI:10.3969/j.issn.1672-1144.2016.01.013