引入判别准则的主动轮廓分割模型

赵方珍，丁德红,2，李立信，卢利莉



引入判别准则的主动轮廓分割模型

赵方珍1，丁德红1,2，李立信1，卢利莉1

（1. 贺州学院计算机科学与信息工程学院，广西 贺州 542899；2. 湖南文理学院计算机科学与技术学院，湖南 常德 415000）

基于区域信息的主动轮廓模型应用在图像分割中，难以使初始轮廓线的鲁棒性和分割强度异质图像的能力实现有效统一。针对这一缺陷，根据Fisher判别准则，在基于全局区域信息和局部区域信息的主动轮廓模型的基础上，对局部区域信息项进行了变换以及引入了判别准则，得到了一种改进的基于区域信息的主动轮廓模型。改进的模型不仅增强了初始位置的鲁棒性，而且可以有效处理强度异质图像，通过实验检验了该模型的性能。

主动轮廓模型；图像分割；判别准则

0 引言

在图像处理和计算机视觉领域，对图像进行有效分割一直是研究的热点。由于图像在成像过程中受到多种因素的干扰，因此图像通常存在强度异质、边缘模糊、含有噪声等问题，这使得许多传统的分割方法对这类图像分割时，效果均不是很理想[1]。近年来，主动轮廓模型在分割这类图像时，展示了较好的分割能力，成为众多图像分割方法中的研究热点之一[2]。

主动轮廓模型可以分为2类：参数主动轮廓模型[3]和几何主动轮廓模型[4]。几何主动轮廓模型又可以细分为2类：基于边缘的动轮廓模型[5-6]和基于区域的主动轮廓模型[4]。基于边缘的主动轮廓模型，在分割弱边缘和含有噪声的图像时，结果不是很理想，并且对初始轮廓线的鲁棒性也较差。为此，学者们提出了基于区域的主动轮廓模型。早期，基于区域的主动轮廓模型中比较有代表性的有CV（Chan-Vese）模型、PS（Piecewise Smooth）模型[7]。CV模型难以分割强度异质图像。PS模型尽管能够处理强度异质的图像，但效率很低。随后，为了能有效分割强度异质图像，Li等[8]提出了局部二值拟合（local binary fitting, LBF）模型，但该模型不仅对初始轮廓线较敏感，而且很容易陷入局部极小值。Wang等[9]考虑到了全局与局部信息，提出了初始位置自适应性较强的局部与全局灰度拟合（local and global intensity fitting, LGIF）模型，使分割更准确。但由于它的能量泛函是非凸的，因此还是极易陷入局部极小值，并且对于不同性质的图像，全局信息与局部信息权重系数的选择比较繁琐，这使得能量泛函对初始位置的选择有一定的依赖性。由于CV模型、LBF模型与LGIF模型具有较为明显的缺陷，因此在一定程度上限制了这些模型的应用范围[10]。

在讨论和分析CV模型、LBF模型与LGIF模型及其算法的基础上，结合Fisher判别准则，得到了一种改进的基于区域信息的主动轮廓模型，将其称为ILGIF（improved local and global fitting）模型。改进模型不仅能有效分割强度异质图像，还对初始位置鲁棒性较高，此外，分割效率也有所提高。

1 相关模型

1.1 CV模型

Chan和Vese提出的CV模型，它假定原始图像是一个分段常量函数。设ÌÂ2为一幅图像域，()为给定的图像，并且():®Â。是图像()在图像域中的一个点。CV模型的能量泛函为：

CV(1,2,)＝1òinside(C)ê()－1½2d＋

2òoutside(C)ê()－2½2d＋ï½(1)

式中：inside()和outside()分别指轮廓的内外区域；1、2分别指inside()、outside()的图像强度均值；1、2和为非负的常数，我们叫前2项为全局数据拟合项。

尽管CV模型对初始位置不敏感，但其没有考虑图像的局部信息，如果轮廓内区域强度异质或者轮廓外区域强度异质或者轮廓内外区域都强度异质，那么CV模型将不会得到正确的分割结果。

1.2 LBF模型

Li等提出的LBF模型以核函数的方式来定义局部二值拟合数据能量项，并将局部数据能量项与变分水平集方法结合，得到最终的LBF模型能量泛函如下：

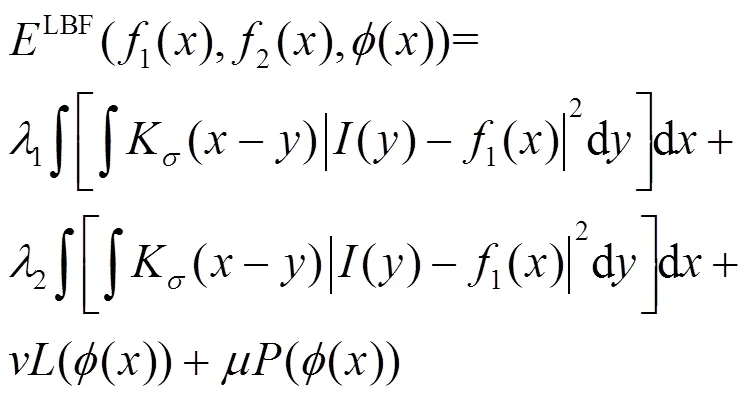
式中：前2项为驱动水平集函数演化的数据能量拟合项；第3项为水平集函数的长度光滑项；第4项为水平集函数的距离规则项；为高斯核函数；为高斯核函数的尺度参数。

尽管LBF模型能有效分割强度异质的图像，但其对初始位置很敏感，并且极易陷入局部极小值而引起误分割，这些缺陷限制了它的广泛应用。

1.3 LGIF模型

Wang等人在CV模型和LBF模型的基础上，提出了LGIF模型，LGIF模型的能量泛函如下：

LGIF(,1,2,1,2)＝(1－)×CV(,1,2)＋

ELBF(,1,2)＋()＋() (3)

式中：CV(,1,2)为CV模型的能量泛函；LBF(,1,2)为LBF模型的能量泛函；()和()为光滑项和距离规则项。参数0≤≤1，当图像的强度异质较大时，取大些，反之则取小些，、为非负常数。

LGIF模型不仅能够有效地分割强度异质的图像，而且初始位置的选择相对LBF模型来说比较灵活，但在分割强度异质图像时，如果初始位置选择不当，能量泛函还是很容易陷入局部极小值。

2 IL2GIF模型

在分析CV模型、LBF模型和LGIF模型的基础上，对LGIF模型进行了适当的变换，并且引入了判别准则函数，得到了改进模型，即ILGIF模型，其能量泛函如下式：

(,1,2,1,2)＝(1－)G＋EL＋R＋J(,1,2) (4)

式中：为水平集函数；、均为非负的常数，0≤≤1，0≤≤1；G为全局信息项，其实质是CV模型的能量泛函；L为局部信息项，其实质是经过变换的LBF模型的能量泛函；R为水平集函数的规则项；为引入的判别准则函数项。

G的表达式如下式：

G(,1,2)＝òinside(C)ê()－1½2[()]d＋

òoutside(C)ê()－2½2{1－[()]}d(5)

式中：1和2的表达式如下：

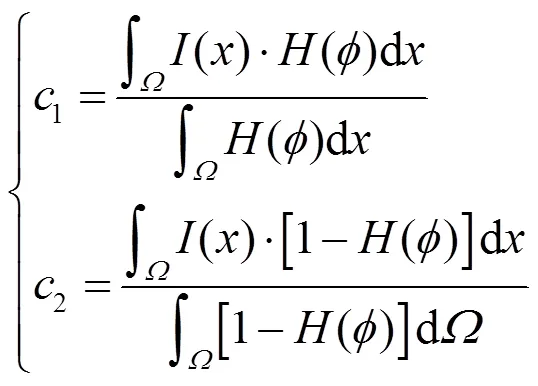
L的表达式如下：

L(,1,2)＝òinside(C)êk*()－()－1½2[()]d＋

òoutside(C)êk*()－()－2½2{1－[()]}d(7)

式中：()是待分割图像；k是一个均值滤波器；0()＝k*()－()的实质是将经过均值滤波的待分割图像与原待分割图像作差，经此变换，提高了待分割图像目标区域和背景区域的对比度，减弱了图像的强度异质成度，这在分割强度异质图像时，能有效提高分割精度。

R的表达式如式(8)所示：

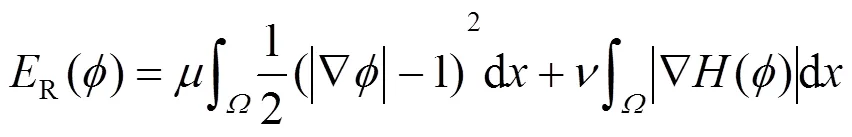
的表达式如下：

式中：0()＝k*()－()；1、2分别为曲线内外的像素数；1、2为曲线内外的像素值，其表达式分别如式(10)、(11)：

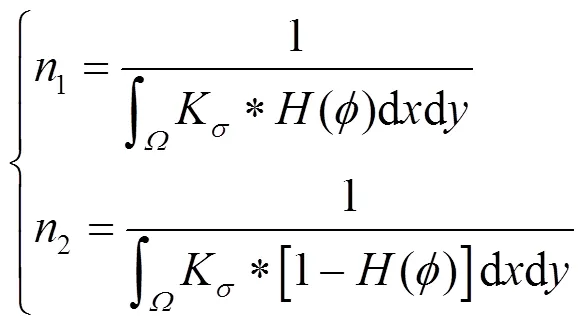
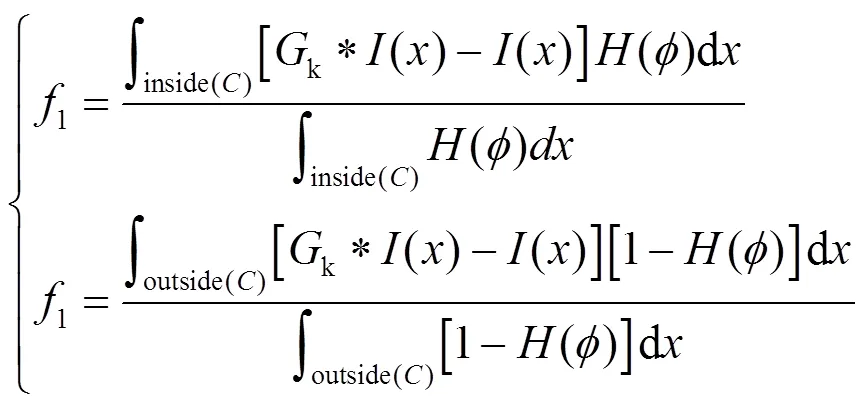
式中：是一个高斯核函数，其表达式如下：

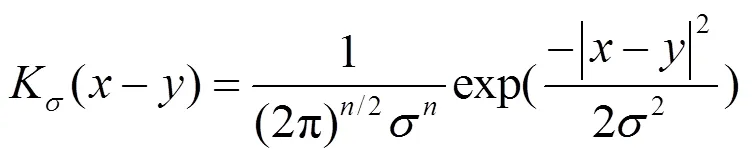
该判别准则函数的实质是一个经过变换的fisher准则函数。Fisher判别准则的目的是求解一个最优的判别向量，使得投影后类间散布距离与类内散布距离的比值最大。Fisher判别准则能获得最有利的分类模式，适用于分类问题[11-12]。

对于二相分割问题，每个像素将被划分为目标类或背景类，CV模型、LBF模型和LGIF模型近似于将类内的差异最小化的分类问题。当曲线演化时，会把图像分为曲线内和曲线外两部分，即把图像分成2类。CV模型相当于用全局强度均值信息表示曲线内外的类内离散度的和，LBF模型相当于用局部强度均值信息表示曲线内外的类内离散度的和，LGIF模型相当于用全局强度均值信息和局部强度均值信息来表示曲线内外的类内离散度的和。理论上，CV模型、LBF模型和LGIF模型的变分泛函能够取得全局最小值，即类内离散度最小。但由于这3种模型所利用的图像区域信息比较少，往往会引起过分割或边缘泄露。为此，引入了在表达形式上与Fisher判别准则极其相似的判别准则函数。

通过分析(9)式可知，分母(1－2)2相当于是Fisher判别准则中的类间离散度，分子相当于是Fisher判别准则中的类内离散度，当能实现最优分类时，分母会取得极大值，分子会取得极小值，此时分子与分母的比值会取得极小值，与主动轮廓模型通过求解其能量泛函的极小值来实现目标轮廓的提取完全吻合。

对式(4)进行全变分以及采用梯度下降流算法进行最小化，得到ILGIF模型的水平集函数演化方程如下：

式中：为水平集函数；0()＝k*()－()；k是一个均值滤波器；、、、均为非负的常数，0≤≤1，。第1项为图像数据驱动力项，第2项为判别准则信息项，第3项为水平集函数的长度光滑项，第4项为水平集函数的距离规则项，()是狄拉克函数。

一般情况下，狄拉克函数()满足()＝¢()，()为Heaviside函数，这2个函数的表达式分别如下：

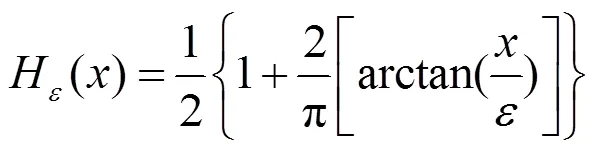
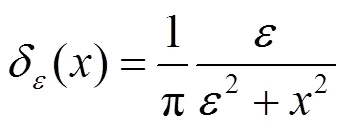
综上所述，ILGIF模型的具体实现过程如下：

Step1：初始化水平集函数；

Step2：用(6)式更新1和2；

Step3：用(11)式更新1和2；

Step4：用(10)式更新1和2；

Step5：用(13)式迭代更新水平集函数直到满足收敛条件，否则返回Step2。

3 实验结果与分析

实验平台为Windows7＋MATLAB7.1，计算机的主要配置为：Intel(R) Core（TM）i5-4210U，主频2.7GHz、内存4.0G。

为了检验DLGIF模型的有效性和性能，将该模型分别应用到合成图像与医学图像中。所有实验采用的时间步长均是D＝0.1，＝1，1＝2＝3＝4＝1，＝3，均值滤波器中的＝25，水平集函数都初始化成值为2的二值函数。图中的浅色曲线均表示初始轮廓线，深色曲线均表示最终轮廓线，相关实验的参数设置如表1所示。

表1 实验过程中的参数设置

3.1 ILGIF模型在合成图像中的实验结果与分析

为了说明ILGIF模型对初始位置有很好的鲁棒性，将ILGIF模型应用到与图1性质完全一致的合成图像中。将ILGIF模型的实验结果与CV、LBF和LGIF模型的实验结果做比较，4种模型在不同的初始位置所得的曲线演化结果如图1所示。

图1中，(a)为原图像，(b)为原图像经过均值滤波之后与原图像相减得到的图像，(a1)(a2)、(b1)(b2)、(c1)(c2)和(d1)(d2)分别对应着CV、LBF、LGIF和ILGIF模型在2个不同初始位置进行曲线演化的结果，a'(1) a'(2)、b'(1) b'(2)、c'(1) c'(2)和d'(1) d'(2)分别对应着4种模型曲线演化后得到的二值图像。从图中可以看出，CV模型几乎不具备分割强度异质合成图像的能力，LBF和LGIF模型均有一定分割强度异质合成图像的能力，但分割的效果不是很好，而ILGIF模型在不同的初始位置对强度异质合成图像均能得到很好的分割结果。

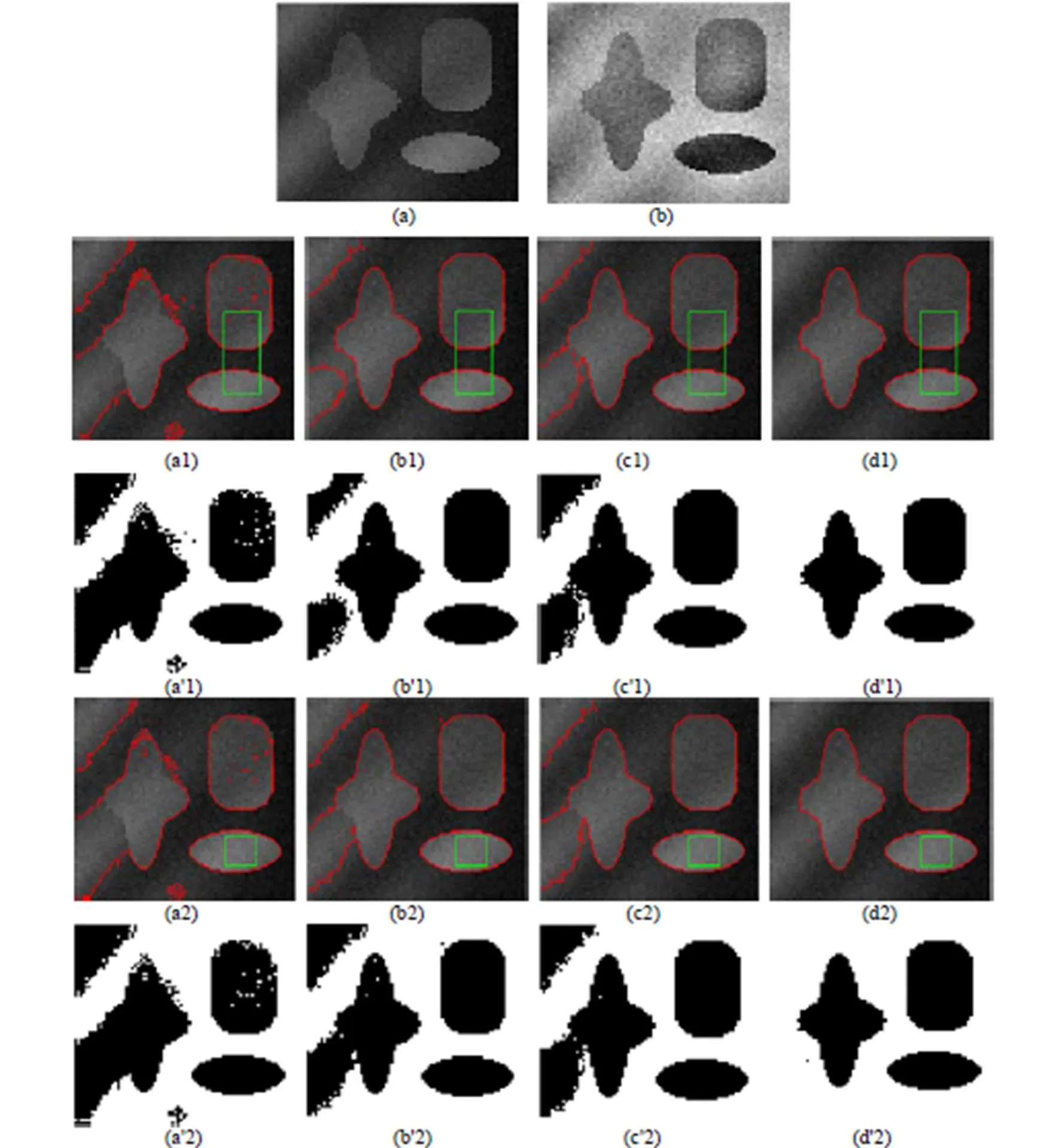
图1 CV、LBF、LGIF和ILGIF模型对强度异质合成图像在不同初始位置进行曲线演化得到的结果

3.2 ILGIF模型在医学图像中的实验结果与分析

为了说明ILGIF能有效分割强度异质图像，将ILGIF模型应用到真实的医学图像中，分别用CV、LBF、LGIF和ILGIF模型，对一幅真实的X射线拍得的血管图像，选择2个不同的初始位置进行曲线演化。将ILGIF模型的实验结果与CV、LBF和LGIF模型的实验结果做比较，4种模型的曲线演化结果如图2所示。

图2中，(a)为原图像，(b)为原图像经过均值滤波之后与原图像作差得到的图像，(a1)(a2)、(b1)(b2)、(c1)(c2)和(d1)(d2)分别对应着CV、LBF、LGIF和ILGIF模型在不同的初始位置进行曲线演化的结果，a'(1) a'(2)、b'(1) b'(2)、c'(1) c'(2)和d'(1) d'(2)分别对应着4种模型曲线演化后得到的二值图像。从图片组的目视效果比较可以得出：CV模型几乎不能分割此类强度异质的血管图像，LBF模型和LGIF模型展示了一定的分割真实血管图像的能力，但b'(1) b'(2)和c'(1) c'(2)的下部即末稍部分不能分割，分割效果与本文的ILGIF模型相比，明显要差。

图2 CV、LBF、LGIF和ILGIF模型对血管图像在两个不同初始位置进行曲线演化得到的结果

为了说明ILGIF模型对比较复杂的医学图像也具有良好的分割效果，将CV、LBF、LGIF和ILGIF模型对另一幅X射线拍得的血管图像进行分割，选择2个不同的初始位置，曲线演化的结果如图3所示。

图3中，(a)为原图像，(b)为原图像经过均值滤波之后与原图像作差得到的图像，图3(a)、(b)纹路上看较图2(a)、(b)要复杂，a(1) a(2)、b(1) b(2)、c(1) c(2) 和d(1)d(2)分别对应着CV模型、LBF模型、LGIF模型和ILGIF模型在2个不同初始位置对同一幅血管图像进行曲线演化的结果，a'(1) a'(2)、b'(1) b'(2)、c'(1) c'(2)和d'(1) d'(2)分别对应着4种模型曲线演化后得到的二值图像。从图中可以看出，CV模型不能对这类图像进行分割，LGIF模型虽然对这类图像有一定的分割能力，但却很容易陷入局部极小值，LBF模型能分割这类图像，较LGIF分割效果要好，但与ILGIF模型的分割结果相比，分割的精度还有待提高，ILGIF模型的分割能力相对最优。

图3 CV、LBF、LGIF和ILGIF模型对血管图像在不同初始位置进行曲线演化得到的结果

为了进一步检验DLGIF模型在处理强度异质医学图像上的性能，将DLGIF模型应用到一幅强度异质较大的脑核磁共振图像（magnetic resonance Image, MRI）中，选择2个不同的初始位置进行曲线演化实验。图4显示了CV、LBF、LGIF和ILGIF模型在两个不同初始位置对脑MRI进行曲线演化得到的结果。

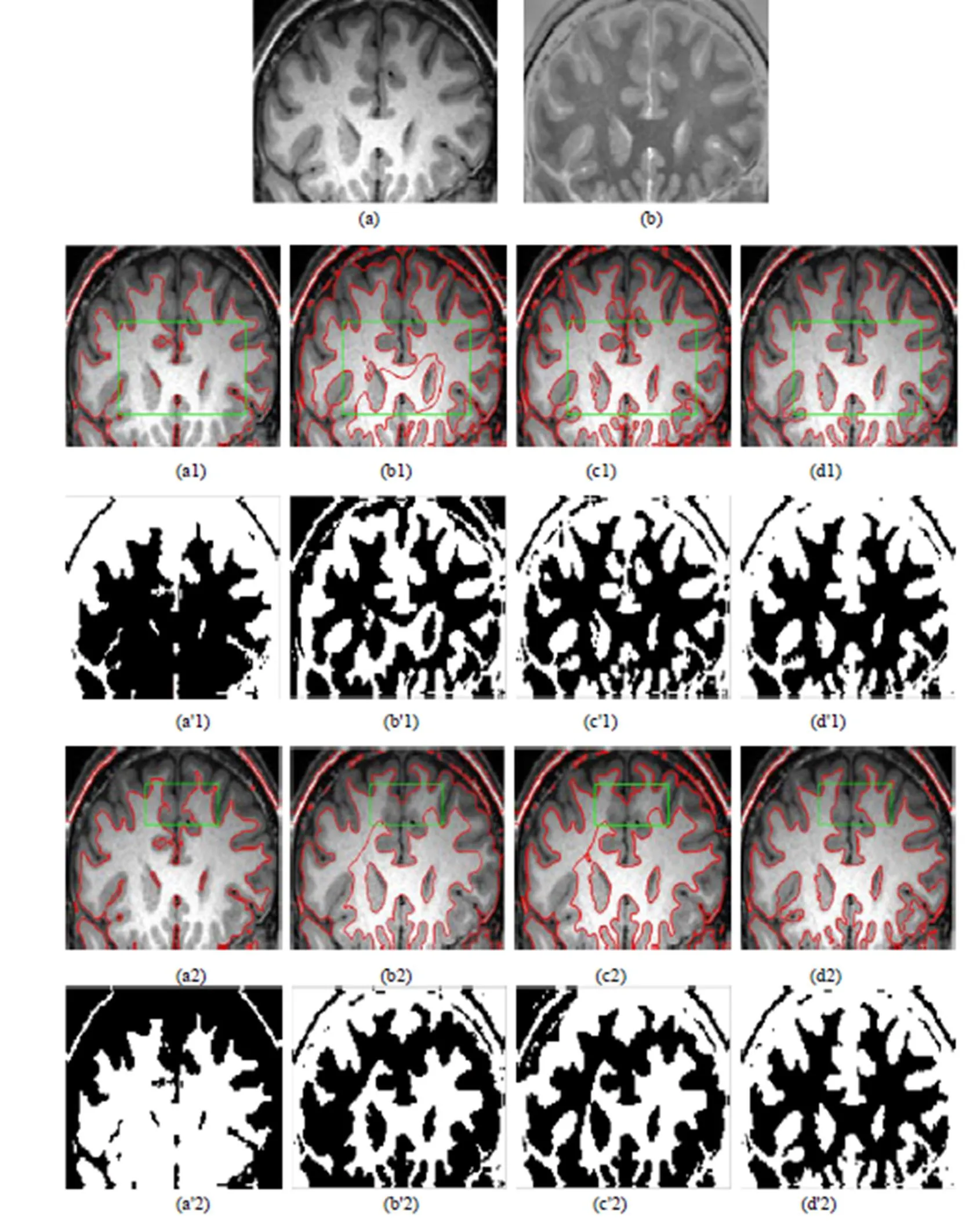
图4 CV、LBF、LGIF和ILGIF模型对脑MRI在不同初始位置进行曲线演化得到的结果

图4中，(a)为原图像，(b)为原图像经过均值滤波之后与原图像作差得到的图像，a(1) a(2)、b(1) b(2)、c(1) c(2)和d(1)d(2)分别对应着CV、LBF、LGIF和ILGIF模型在两个不同的初始位置对脑MRI进行曲线演化得到的结果，a'(1) a'(2)、b'(1) b'(2)、c'(1) c'(2)和d'(1) d'(2)分别对应着4种模型曲线演化后得到的二值图像。从图中可以看出，CV模型基本上不具备分割这类图像的能力，LBF模型分割的结果不理想，LGIF模型的分割结果相比LBF模型有了很大的改善，但是分割的效果仍然不是很理想，比较得出ILGIF模型的分割效果较另外3种都要好，能将脑白质有效地分割出来。

4 结论

以主动轮廓模型初始位置的鲁棒性和强度异质图像的分割能力为研究对象，分析了CV模型、LBF模型和LGIF模型的不足，在借鉴Fisher原理的基础上引入判别准则函数，提出了ILGIF模型。针对初始位置任定、不同强度异质、不同复杂程度3种情况，分别用人工合成图像与医学图像进行了对比实验，得出该模型与CV模型、LBF模型和LGIF模型相比，具有对初始位置不敏感、能有效分割不同强度异质图像、分割的准确度高以及分割效果显著等更好的性能，验证了ILGIF模型的有效性。本研究成果将进一步用于森林资源监测和红外目标识别。

[1] 纪利娥, 杨风暴, 王志社, 等. 基于边缘图像和SURF特征的可见光与红外图像的匹配算法[J]. 红外技术, 2012, 34(11):629-635.

JI Li’e, YANG Fengbao, WANG Zhi-she, et al. Visible and infrared image matching algorithm based on edge image and SURF features[J]., 2012, 34(11):629-635.

[2] WANG X F, MIN H, ZOU L, et al. A novel level set method for image segmentation by incorporating local statistical analysis and global similarity measurement[J]., 2015, 48(1):189-204.

[3] Kass A W M, Terzopoulos D. Snakes: active contour models[J]., 1987(4): 321-331.

[4] Chan T, Vese L. Active contours without edges[J]., 2001, 10(2): 266-277.

[5] Caselles V, Kimmel R, Sapiro G. Geodesic active contours[J]., 1997, 22: 61-79.

[6] Xu C, Prince J L. Snakes，shapes and gradient vector flow[J]., 1998, 7(3): 359-369.

[7] Vese L A, Chan T F. A multiphase level set framework for image segmentation using the Mumford and Shah model[J]., 2002, 50(3): 271-293.

[8] Chunming L, Chiu-Yen K, Gore J C, et al. Implicit active contours driven by local binary fitting energy[C]//, CVPR, 2007: 1-7.

[9] Wang L, Li C, Sun Q, et al. Active contours driven by local and global intensity fitting energy with application to brain MR image segmentation[J]., 2009, 33(7): 520-531.

[10] Yue X, Xie M, Li L. Improved LBF model combined with Fisher criterion[M]//Jin D , Lin S., Berlin Heidelberg: Springer, 2012, 1: 1-5.

[11] Qingshan L, Rui H, Hanqing L, et al. Face recognition using Kernel- based Fisher Discriminant Analysis[C]//, 2002: 197-201.

[12] Qingshan L, Hanqing L, Songde M. Improving kernel Fisher discrimi- nant analysis for face recognition[J]., 2004, 14(2): 42-49.

The Active Contour Segmentation Model with Criterion Introduced

ZHAO Fangzhen1，DING Dehong1,2，LI Lixin1，LU Lili1

(1.,,, 542800,;2.,,, 415000,)

In image segmentation, active contour model based on regional information application is difficult to make the robustness of initial contour line and the ability of segmenting heterogeneous image segmentation unified effectively. In view of these disadvantages, according to the principle of Fisher discriminant criterion, this paper gets an improved active contour model based on regional information, which is on the basis of active contour model with the global regional information and local regional information, by transforming local regional information item and introducing the discrimination criterion information. The improved model not only enhances the initial position of robustness, but also can effectively deal with intensity heterogeneous image. The property of this model is verified by experiments.

active contour model，image segmentation，discrimination criterion

TP391.4

A

1001-8891(2016)04-0325-08

2015-08-13；

2015-09-21.

赵方珍（1987-），女，广西桂林人，硕士研究生，主要研究方向：电子技术与图形图像处理。E-mail：747128688@qq.com。

广西高校科研项目（KY2015ZD127）；湖南文理学院博士科研启动基金项目；广西高校科学技术研究项目重点项目（ZD2014129）。